Pour déterminer l'existence
éventuelle d'une intersection:
(1) calculer le rayon réfléchi,
(2) utiliser ce rayon pour tester son intersection vis à vis de la sphère,
(3) si cette intersection existe, déterminer sa position.
(1) On utilise la formule ![]() où
où![]() est le vecteur normé inverse à la direction d’incidence
de la source lumineuse,
est le vecteur normé inverse à la direction d’incidence
de la source lumineuse, ![]() est le vecteur normé
réfléchi, et
est le vecteur normé
réfléchi, et ![]() est
la normale à l’interface orientée dans la matériau d'où se propage le rayon
incident.
est
la normale à l’interface orientée dans la matériau d'où se propage le rayon
incident.
![]() se calcule en normant le vecteur
D-L.
se calcule en normant le vecteur
D-L. ![]() est
orthogonal au plan du miroir et est obtenu en normant le résultat du produit vectoriel de
(D-A) par (D-B) et en ajustant son orientation pour qu'elle soit dirigée dans le demi
plan délimité par le miroir et contenant le rayon
est
orthogonal au plan du miroir et est obtenu en normant le résultat du produit vectoriel de
(D-A) par (D-B) et en ajustant son orientation pour qu'elle soit dirigée dans le demi
plan délimité par le miroir et contenant le rayon ![]() .
.
Par ces calculs on obtient ![]() = (0.274, 0.961,
0.0) et
= (0.274, 0.961,
0.0) et ![]() =
(0.447, 0.894, 0.0). Ce qui conduit à
=
(0.447, 0.894, 0.0). Ce qui conduit à ![]() = (0.604, 0.796, 0.0).
= (0.604, 0.796, 0.0).
(2) Le rayon réfléchi est issu de D
et a pour direction ![]() = (0.604, 0.796, 0.0). Il faut résoudre le système d'équations formé de
l'équation paramétrique de la droite définie par le rayon et de l'équation euclidienne
de la sphère:
= (0.604, 0.796, 0.0). Il faut résoudre le système d'équations formé de
l'équation paramétrique de la droite définie par le rayon et de l'équation euclidienne
de la sphère:
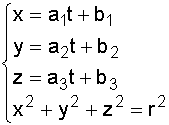
où (a1, a2, a3)
est la direction du rayon, cest à dire ![]() et (b1, b2, b3)
son origine, c'est à dire D.
et (b1, b2, b3)
son origine, c'est à dire D.
Tel que présenté ci-dessus, la sphère est centrée sur l'origine. Or dans notre cas, la sphére est centrée sur (12, 6, 0). Un traitement préalable consistera donc à ramener la sphère à l'origine par translation de (-12, -6, 0). Cette opération sera aussi appliquée à l'origine du rayon (D) pour conserver la cohérence des données. Après détermination de l' (des) intersection(s), une translation inverse permettra de trouver la (les) véritable(s) position(s).
On a donc r = 1, a1= 0.604387, a2= 0.796691, a3= 0.0, b1= -10.0, b2= -5.0, b3= 1.0
Par substitution dans le système, on obtient:(a1t + b1)2+(a2t + b2)2+(a3t + b3)2 = r2
(a12+a22+a32)t2 + 2(a1b1+a2b2+a3b3)t + b12+b22+b32 = r2
équation du second degré en t impliquant 0, 1 ou 2 intersections en fonction des conditions initiales.
On pose a = (a12+a22+a32), b = 2(a1b1+a2b2+a3b3), c = b12+b22+b32-r2.
-> a = 1.0, b = -20.054642 et c = 125.0
La valeur du déterminant delta = b2-4ac
définit le nombre d'intersections:
- delta < 0 -> pas d'intersection,
- delta = 0 -> une intersection,
- delta > 0 -> deux intersections.
-> delta = -97.081 donc pas d'intersection.
Si delta > 0, on calcul les racines t1 = (-b-sqrt(delta))/(2*a) et t2 = (-b+sqrt(delta))/(2*a). t1 et t2 sont ensuite réutilisées comme paramètres dans l'équation paramétrique de la droite permettant ainsi de trouver les positions des deux intersections après translation par (12,6,0).
Si delta = 0, on calcul la racine t = -b/(2*a). t est ensuite réutilisée comme paramètre dans l'équation paramétrique de la droite permettant ainsi de trouver la position de l'intersection après translation par (12,6,0).
Programme
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr