Sujets et corrections
de TD et TP
![]()
|
Fichier zip |
TP n°1 et TP n°2 : Premières implantations OpenGL
Exercice n°1
Télécharger le fichier archive IG-2024-2025.zip. Ce fichier archive contient une "solution" Visual Studio 2022. Une solution est un package destiné à référencer
des projets de développement Visual Studio (exécutables, librairies, dll, drivers..., mais aussi éventuellement sites web statiques ou dynamiques). La concrétisation physique d'une solution est formée
a minima d'un fichier .sln quand elle ne contient aucun projet de développement. Elle consistera plus généralement en un fichier .sln, en les fichiers .vcxproj des projets qu'elle inclut et en
les fichiers (source ou autre) nécessaires à la compilation de ces projets. Il est bon que tout cela soit organisé physiquement en répertoires pour que tout ne soit pas mélangé.
Après extraction, un répertoire IG-2024-2025 est créé. Ce répertoire contient lui-même 6 répertoires :
- Bin pour les exécutables générés,
- Include pour les fichiers d'entête OpenGL (fichiers non présents par défaut dans Visual Studio),
- Lib pour les fichiers librairie OpenGL (fichiers non présents par défaut dans Visual Studio),
- Projet pour le fichier de description de la solution (Projet.sln, ...) et les répertoires contenant les projets faisant partie de la solution (Un seul répertoire actuellement : Exemple),
- Src pour les fichiers source des projets inclus dans la solution,
- Temp pour les fichiers temporaires (compilation, ...).
Le contenu de la solution peut être visualisé dans Visual Studio en utilisant l'explorateur de solution (item supérieur du menu Affichage). La solution IG-2024-2025 comprend
un seul projet de développement nommé Exemple. Ce projet référence un seul fichier source Exemple.cpp et est préconfiguré pour une compilation utilisant OpenGL :
- utilisation des fichiers d'entête (répertoire implicite ../../Include),
- utilisation des fichiers librairie : OpenGL32.ms.lib et glu32.ms.lib dans les propriétés de configuration du projet et glut32.ms.lib par référence directe dans l'explorateur de solution,
- copie post édition de liens dans le répertoire Bin de l'exécutable généré lors de l'édition de liens dans un sous-répertoire du répertoire Temp.
IG-2024-2025 est donnée intégralement préconfigurée car, même si les manipulations visant à configurer les options de compilation et d'édition de liens spécifiques à OpenGL
sont interessantes en tant que telles, elles sortent du champ de ce TP.
Attention, contrairement à d'autres gestionnaires de projets, l'explorateur de solution ne se base pas sur l'organisation physique des fichiers sur leur(s) support(s) de stockage pour l'affichage
en onglets et sous-onglets. L'explorateur de solution se contente de référencer ces fichiers (relativement au répertoire dans lequel se trouve le fichier sln -> solution globalement déplaçable)
et permet de créer des onglets (des filtres) pour organiser l'ensemble des références nécessaires à la compilation. Rien n'oblige à ce que la structure en arborescence des filtres soit mappée
sur la structure en arborescence de répertoires du stockage des fichiers. Rien ne permet de faire créer automatiquement les onglets du gestionnaire de solution sur la base de l'organisation en arborescence
de répertoires du stockage des fichiers.
La génération (compilation puis édition de liens) de ce projet doit conduire à la création d'un exécutable nommé Exemple.exe dans le répertoire Bin. Son exécution requière les dll OpenGL32.dll et
Glu32.dll (toujours présentes par défaut dans le système d'exploitation Windows) ainsi que la dll Glut32.dll (jamais présente par défaut dans le système d'exploitation Windows mais dont il existe
une copie dans le répertoire Bin où est copié l'exécutable).
1) Extraire l'archive IG-2024-2025.zip. Lancer Visual Studio et charger la solution. Elle est théoriquement compatible avec les versions 2015, 2017, 2019 et 2022 de
Visual Studio au prix d'une conversion qui devrait être proposée lors du premier chargement.
Vérifier la compilation et l'exécution du projet Exemple.
2) Le fichier code source GLUtMinimum.cpp illustre le fonctionnement événementiel de la librairie GLUt. On rappelle que nous allons utiliser cette librairie annexe à OpenGL pour construire l'interface utilisateur de nos programmes OpenGL, celui-ci ne contenant aucune fonction dédiée à cette fin.

Le fichier source GLUtMinimum.cpp contient le minimum possible d'appels à OpenGL tout en affichant quand-même quelque chose, de façon à mettre en évidence les fonctionnalités GLUt et non les fonctionnalités OpenGL.
a) Télécharger le fichier GLUtMinimum.cpp. Repérer dans le code les appels de fonction qui semblent correspondre aux fonctionnalités implantées listées ci-dessous en italique. Placer des commentaires dans le code pour garder une trace de ce que vous avez repéré.
La scène construite est constituée d'un unique tore muni du matériel par défaut d'OpenGL. Le calcul d'illumination est activé et une seule lumière est allumée. L'élimination des parties
cachées est activée. La projection est réalisée en projection orthographique. Le contenu du volume cubique dont la diagonale est définie par les positions (-1.0,-1.0,-1.0) et (1.0,1.0,1.0) du repère de
modélisation est affiché dans le viewport de visualisation (la fenêtre) en projection selon l'axe -z du repère de modélisation. Le viewport de visualisation est configuré pour occuper automatiquement
(dynamiquement) l'intégralité de la fenêtre.
La fonction main organise les points suivants :
- exécution d'une fonction (static void clean(void)) lorsque l'application est interrompue par exécution de la fonction standard void exit(int),
- configuration et création de la fenêtre de visualisation,
- configuration des paramètres OpenGL obligatoires qui n'auront pas à être reconfigurés au cours de la vie du programme (appels regroupés dans la fonction static void init(void)),
- programmation de la gestion des événements,
- affichage de la fenêtre de visualisation et lancement de la boucle infinie de gestion des événements.
Les événements suivants sont gérés "normalement" avec exécution de code OpenGL valide et cohérent :
- rafraichissement de la fenêtre de dessin (display),
- modification de la taille de la fenêtre de dessin (reshape).
Les événements suivants sont gérés a minima par des échos écran en texte de messages dans la console d'exécution de façon à permettre la trace du fonctionnement du programme :
- frappe d'une touche alphanumérique du clavier (keyboard),
- frappe d'une touche non-alphanumérique du clavier (special),
- clic souris dans la fenêtre de dessin (mouse),
- déplacement de la souris bouton appuyé dans la fenêtre de dessin (mouseMotion).
Le code de gestion des événements suivants est programmé pour une gestion a minima par affichages écran texte de messages dans la console, mais ces événements ne sont pas activés (lignes laissées en commentaire)
dans la fonction main :
- aucun événement n'est en attente (idle),
- déplacement de la souris bouton non appuyé devant la fenêtre de dessin (passiveMouseMotion).
b) Remplacer le fichier Exemple.cpp par le fichier GLUtMinimum.cpp dans le projet VisualStudio. Vérifier que la compilation et l'exécution fonctionnent.
Le fichier GLUt-3-spec.pdf contient la documentation de référence de GLUt. Il pourra vous aider à implanter les réponses aux questions c) à g).
De par sa nature non orientée objet la librairie GLUt ne peut pas être employée sans utiliser des variables globales. Celles-ci permettent le partage d'informations entre les différentes fonctions
implantées pour être exécutées en réponse aux événements. De façon à ne pas aller contre le fonctionnement événementiel de GLUt mais plutôt à s'inscrire dans son cadre, on évitera de s'autoriser
à placer des instructions OpenGL dans toutes les fonctions événementielles et on limitera un tel placement aux seules fonctions display (rafraichissement de la fenêtre de dessin) et reshape (changement
de la taille de la fenêtre de dessin). Il est naturel que ces deux fonctions aient à contenir de l'OpenGL car la fonction reshape devra configurer la caméra virtuelle de visualisation OpenGL et la
fonction display devra modéliser la scène en OpenGL. Au lancement de l'application, GLUt entre en boucle infinie après post automatique d'un événement reshape et d'un événement display. Il
exécute donc la fonction reshape puis la fonction display, et se met en attente d'événements. Les événements peuvent arriver à n'importe quel instant et être de n'importe quel type lorsqu'ils
arrivent y compris des reshape et des display. Placer des instructions OpenGL dans d'autres fonctions que reshape et display n'est pas interdit mais présenterait pour inconvénient de générer un
flux OpenGL plus difficile à rendre déterministe, nous allons donc éviter de le faire.
Notre méthode de programmation consistera :
- à utiliser des variables globales dont les valeurs ne seront jamais modifiées mais simplement utilisées telles quelles pour les appels de fonction OpenGL dans les fonctions reshape et display
(principalement dans display) pour paramétrer la modélisation et ses paramètres,
- à modifier (et donc aussi utiliser) ces variables globales dans les autres fonctions de réaction aux événements et à ne jamais faire d'appels de fonction OpenGL dans ces fonctions.
En opérant ainsi, le flux d'exécution des fonctions événementielles qui aurait par exemple été :
RDKDISRDMMMMKKDRDIDIDIDIKD
se réduira au flux :
RDDRDDRDDDDD
pour les seules fonctions qui contiennent de l'OpenGL à savoir reshape et display. On n'obtient toujours pas un ordre déterministe pour les fonction OpenGL mais cette restriction auto-imposée
permet de faciliter notre travail de conception quand il s'agit de s'assurer et d'obtenir la cohérence d'exécution OpenGL au sein d'un fonctionnement événementiel aléatoire du point
de vue de l'ordre d'arrivée des événements.
Un autre intérêt de cette restriction est que si vous abandonnez GLUt pour une autre librairie de fenêtrage, le portage vers cette nouvelle librairie sera facilité.
c) Implanter un contrôle clavier permettant de switcher entre les modes d'affichage plein et fil de fer en utilisant la touche de clavier Espace.
Il convient de modifier la fonction keyboard du fichier source et d'utiliser la fonction OpenGL glPolygonMode pour le paramétrage du mode d'affichage
dans la fonction display.
d) Implanter une animation telle que le tore tourne sur lui-même autour de l'axe Ox à raison de 1° de rotation entre chaque image.
Il convient d'adapter la fonction idle et de programmer son exécution en tâche de fond dans la fonction main. La fonction OpenGL glRotatef sera utilisée
dans la fonction display juste avant l'appel à la fonction scène pour réaliser la rotation de celle-ci. Appeler soi-même la fonction display ou, encore pire, programmer une boucle explicite autour
d'un appel à la fonction display est totalement proscrit car cela contrecarrerait le fonctionnement événementiel. Dans la fonction idle on utilisera la fonction GLUt glutPostRedisplay pour poster
un événement redisplay, entrainant ainsi l'exécution de la fonction display par GLUt sitôt que ce sera possible, et obtenant ainsi un flux d'exécution événementiel qui sera IDIDIDIDIDIDIDID et
dont il résultera une animation.
e) Implanter un contrôle clavier permettant d'activer/désactiver l'animation au moyen de la touche Entrée.
On s'inspirera de la méthode utilisée dans Exemple.cpp.
f) Implanter un contrôle clavier permettant de faire tourner interactivement le tore sur lui-même autour de l'axe Oy dans un sens ou dans l'autre en utilisant les touches Flèche gauche
et Flèche droite du clavier. On pourra par exemple appliquer une rotation de 1° ou de -1° à chaque utilisation d'une des flèches.
Il convient d'adapter la fonction special.
g) Implanter un contrôle permettant de faire tourner le tore sur lui-même autour de l'axe Oy en réaction aux mouvements horizontaux de la souris bouton gauche appuyé à raison de 1° de
rotation par pixel de déplacement.
Il convient d'adapter les fonctions mouse et mouseMotion.
h) Compléter le contrôle souris de la question g) pour faire tourner le tore sur lui-même autour de l'axe Ox en réaction aux mouvements verticaux de la souris bouton gauche appuyé à raison de 1° de rotation par pixel de déplacement. Compléter une nouvelle fois le contrôle souris pour qu'un clic du bouton droit entraine le changement de sens du mouvement de rotation automatique.
i) Ajouter un contrôle clavier permettant d'utiliser les touches n, m, N et M pour augmenter et diminuer les nombres de facettes du tore (en longitude pour n et N, en latitude pour m et M).
j) Ajouter un contrôle clavier d'activation/désactivation de l'élimination des parties cachées. Ajouter un contrôle clavier d'activation/désactivation de la gestion des lumières.
|
GLUT |
||
| Fonctionnalités principales de GLUt : - création de fenêtres - gestion des événements : - fenêtre - clavier - souris |
||
![]()
TD n°1 : Modélisation géométrique par objets canoniques, premières scènes OpenGL
Exercice n°1
(1) Programmer en OpenGL la scène suivante sous la forme d'une fonction C sans utiliser les fonctions glPushMatrix et glPopMatrix ailleurs qu'en début et fin de fonction :
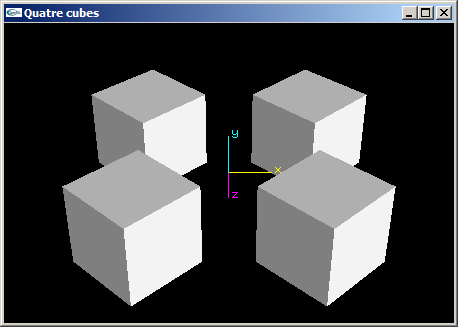
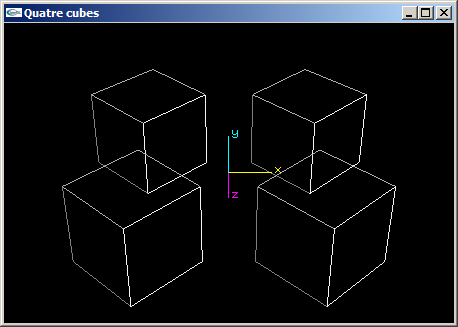
Quatre cubes de côté 2.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0). Les cubes ont leurs faces orthogonales aux axes du repère de modélisation.
(2) Reprogrammer en OpenGL la scène de la question (1) de telle manière que les cubes aient une de leurs faces orientée vers l'origine du repère.
(3) Reprogrammer en OpenGL la scène de la question (2) en utilisant les fonctions glPushMatrix et glPopMatrix pour rendre les objets indépendants les uns des autres et simplifier l'écriture de la fonction scène.
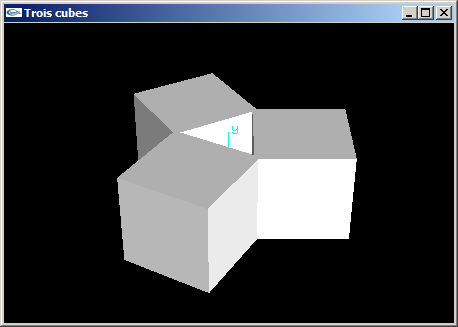
(4) Programmer une scène OpenGL en plaçant 3 cubes de côté 2.0 aux 3 sommets d'un triangle équilatéral défini avec les caractéristiques suivantes :
- rayon 1.5,
- centré sur l'origine,
- plongé dans le plan xOz.
Les 3 cubes présentent une de leurs faces orientée vers l'origine.

Exercice n°2
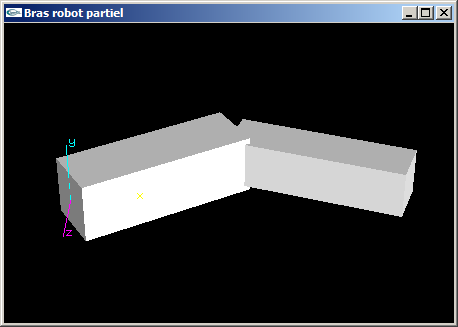
(1) Programmer la scène OpenGL modélisant un bras robot simplifié composé d'un bras et d'un avant-bras.
Le bras est articulé pour que sa base puisse tourner autour de l'axe Oy d'un angle r1. Il s'agit d'un parallélépipède rectangle de dimension (3.0,1.0,1.0).
L'avant-bras est articulé autour de l'axe y au bout du bras pour un angle r2. Il s'agit d'un parallélépipède rectangle de dimension (3.0,0.8,0.8).
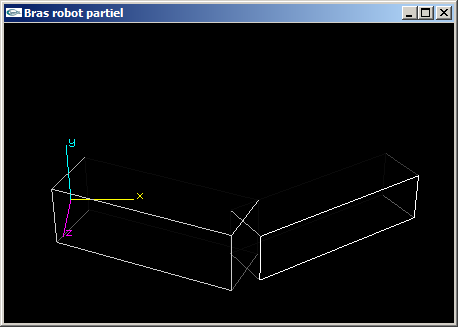
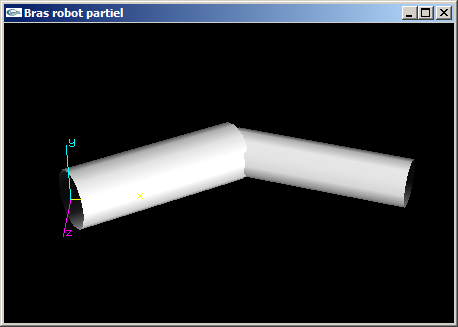
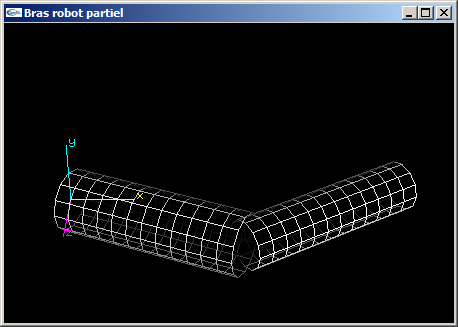
(2) Modifier la fonction OpenGL de l'exercice n°1 en remplaçant les parallélépipèdes par des cylindres de tailles équivalentes à celles des objets qu'ils remplacent.
Exercice n°3 (supplémentaire)
(1) Implanter en OpenGL une fonction de dessin d'une molécule de Benzène (C6H6).
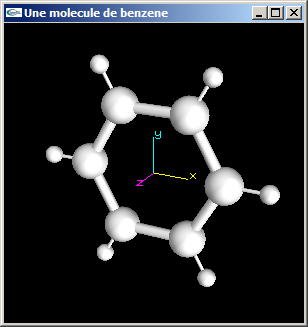
Les atomes de carbone (atomes centraux) ont un rayon égal à 0.5.
Les liaisons entre 2 atomes de carbone ont pour longueur (centre à centre) 2.0 et pour rayon 0.15.
Les atomes d'hydrogène ont un rayon égal à 0.25.
Les liaisons entre atome de carbone et d'hydrogène ont pour longueur (centre à centre) 1.2 et pour rayon 0.05.
La molécule est centrée sur l'origine et placée dans le plan xOy.
(2) Modifier la modélisation de la molécule de benzène de la question précédente pour que les liaisons carbone-carbone soient alternativement des liaisons simples et
des liaisons doubles (voir figure ci-dessous).
Les cylindres modélisant ces liaisons auront pour rayon 0.05 (comme les liaisons carbone-hydrogène). Dans le cas des liaisons doubles, les deux cylindres de modélisation seront écartés
de 0.1.
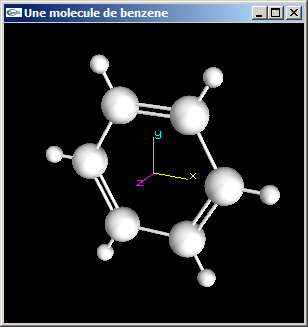
Solutions
| Quatre cubes (Question 3) |
| Trois cubes |
| Bras robot avec parallélépipèdes |
| Bras robot avec cylindres |
| Molécule de benzène |
![]()
TD n°2 : Modélisation géométrique par facettes
Exercice n°1
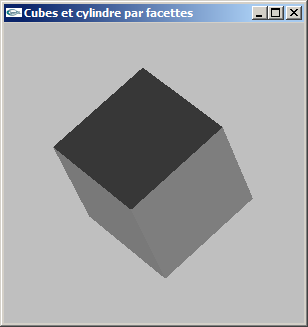
(1) Modéliser par facettes un cube de côté c centré sur l'origine du repère de modélisation. On ne générera pas les normales.
La fonction créée aura pour prototype :
void mySolidCube(double c);
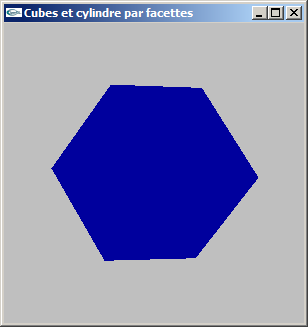
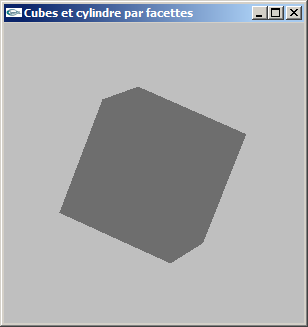
(2) Modifier la modélisation de la question précédente pour ajouter la gestion des normales.
Le but est de rendre possible les calculs d'éclairage.
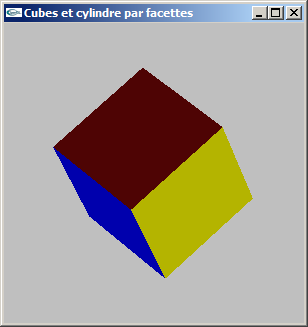
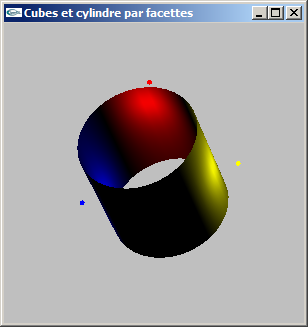
Modéliser par facettes un cylindre selon les caractéristiques suivantes:
- choix du rayon,
- choix de la hauteur,
- choix du nombre de facettes en découpage longitudinal pour une valeur entière ns,
- centré sur l'origine du repère de modélisation,
- axé selon y.
On ne modélisera pas les bases du cylindre, mais uniquement le tube.
La fonction créée aura pour prototype :
void mySolidCylindre(double hauteur, double rayon, int ns);
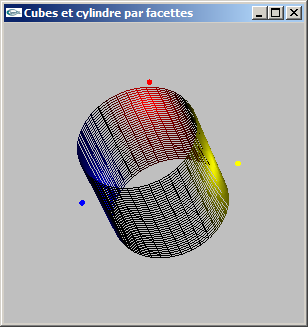
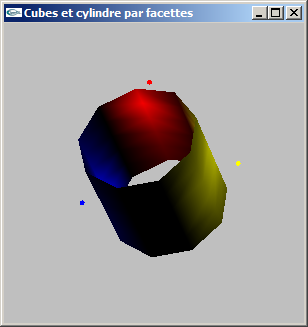
Question supplémentaire : Ajouter un découpage latéral (selon l'axe y) pour une valeur nl.
Le prototype de la fonction devient :
void mySolidCylindre(double hauteur, double rayon, int ns, int nl);
Solutions
![]()
TP n°3 : Modélisation géométrique par objets canoniques
Exercice n°1
(1) Implanter la question n°4 de l'exercice n°1 du TD n°1 (les trois cubes).
(2) Implanter la question n°1 de l'exercice n°2 du TD n°1 (le bras robot). Les cylindres n'étant pas disponibles dans GLUt, on pourra se limiter aux premières questions de l'exercice c'est
à dire celles où des "cubes" sont utilisés. On pourra aussi utiliser des "sphères" (des ellipsoïdes) au lieu de cylindres.
Une des deux fonctions OpenGL permettant de réaliser un zoom sur le repère courant a pour prototype void glScalef(GLfloat rx, GLfloat ry, GLfloat rz). Le zoom
opéré est de rapport rx en x, ry en y et rz en z.
La fonction GLUt permettant la modélisation par facettes d'une sphère est la fonction de prototype void glutSolidSphere(double r, int n1, int n2). Elle
modélise une sphère de rayon r centrée sur l'origine du repère de modélisation courant. Elle crée n1 facettes selon la longitude et n2 facettes selon la latitude.
(3) Implanter des contrôles clavier permettant de modifier les angles r1 et r2 du bras robot de la question n°2. On utilisera les touches '1' et '4' pour augmenter et diminuer r1 et les touches '2' et '5' pour augmenter et diminuer r2.
Exercice n°2
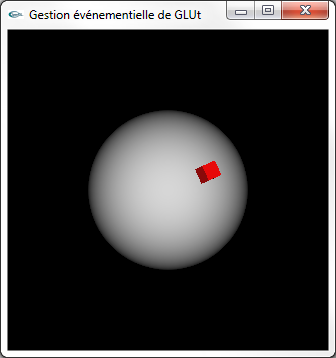
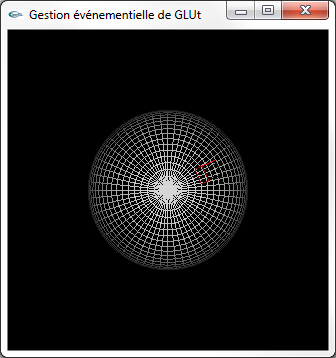
On considère une scène constituée d'une sphère de rayon 0.5 et d'un cube de côté 0.1. La sphère est centrée sur l'origine. Le cube est "posé" sur la sphère (accolé à la sphère) sur l'axe 0z.
Pour la suite de l'exercice, pour changer la couleur des objets et donc mieux les visualiser, on pourra glisser les lignes de codes suivantes
float gris[4] = { 0.8F,0.8F,0.8F,1.0F };
glMaterialfv(GL_FRONT_AND_BACK,GL_DIFFUSE,gris);
avant l'appel à la fonction de modélisation de la sphère et
float rouge[4] = { 1.0F,0.0F,0.0F,1.0F };
glMaterialfv(GL_FRONT_AND_BACK,GL_DIFFUSE,rouge);
avant l'appel à la fonction de modélisation du cube.

(1) Implanter une animation où le cube tourne autour de la sphère (sur la surface de la sphère et autour du centre de la sphère) dans le plan xOz à raison de 2° de rotation entre chaque image.
(2) Modifier l'animation de la question (1) de façon à ce que chaque fois que le cube repasse à sa position initale, son plan de rotation subisse une rotation de 6° autour de l'axe Oz.
Solutions
| Trois cubes |
| Bras robot avec parallélépipèdes |
| Un cube se déplaçant sur une sphère |
![]()
TD n°3 : Matériel et lumières en OpenGL
Tests divers sur les lumières et le matériel d'OpenGL en session interactive :
- Activation des calculs d'illumination et de la lumière n°0.
- Paramétrage des coefficients de réflexion diffuse du matériel
- Paramétrage des coefficients de réflexion spéculaire et de la réflectivité du matériel
- Paramétrage des coefficients de réflexion ambiante du matériel
- Paramétrage des caractéristiques d'émission du matériel
- Mise en évidence de la synthèse additive des réponses en réflexion
- Paramétrage de la lumière n°0 en tant que lumière directionnelle
- Paramétrage de la lumière n°0 en tant que lumière ponctuelle
- Paramétrage de la lumière n°0 en tant que lumière de type spot
- Paramétrage de la lumière n°0 en tant que lumière émettant pour générer des réflexions diffuses
- Paramétrage de la lumière n°0 en tant que lumière émettant pour générer des réflexionx spéculaires
- Mise en évidence du fait que les caractéristiques de position et de direction des lumières sont définies dans le repère courant
-> précaution à prendre qu'en au placement dans le code des appels à glLight* correspondants
-> possibilité de lier les lumières au processus de modélisation géométrique - Mise en évidence de la transparence des surfaces (des objets) aux lumières
-> pas d'ombre portée - Mise en évidence de l'influence de l'existence de facettes sur la qualité de l'éclairage
-> difficile de gérer des détails d'éclairage de taille inférieure à la taille des facettes
![]()
TP n°4 : Modélisation géométrique à base d'ensembles de facettes
Exercice n°1
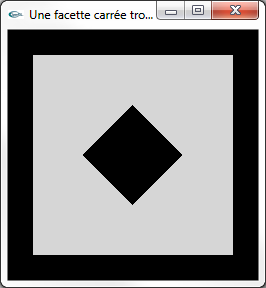
Modéliser par facettes une facette carrée percée d'un trou carré.
Cette facette est plongée dans le plan xOy, centrée sur l'origine du repère de modélisation, de côtés parallèles aux axes x et y et de côtés de longueur 2.0.
Le trou est carré, centré sur l'origine du repère de modélisation, de sommets placés aux positions (0.5,0.0,0.0), (0.0,0.5,0.0), (-0.5,0.0,0.0) et (0.0,-0.5,0.0).
Exercice n°2
a) Implanter et valider la fonction de modélisation d'un cube de l'exercice 1 du TD n°2 (version avec normales).
Vérifier que le résultat obtenu est géométriquement identique au résultat obtenu en utilisant la fonction glutSolidCube de la librairie GLUt.
Tester et expliquer ce qui se passe lorsque les normales ne sont pas spécifées.
b) Implanter la modélisation de cube de la question a) en représentant chacune des 6 faces au moyen d'un maillage de n x n facettes carrées.
c) Implanter et valider la fonction de modélisation d'un cylindre de l'exercice 2 du TD n°2 (version avec normales).
Solutions
![]()
Epreuve n°1 : Modélisation géométrique et animation
![]()
TD n°4 : Programmation de lumières et d'un matériel, calcul de diffusion
Exercice n°1
On souhaite modéliser des lumières au sein d'un programme destiné à réaliser la modélisation de scènes 3D illuminées.
Proposer une hiérarchie de classes C++ permettant de représenter des lumières ponctuelles, des lumières directionnelles et des lumières de type spot.
Définir les attributs de chacune des classes (et les classes nécessaires à la définition de ces attributs).
Exercice n°2
On souhaite modéliser des matériels au sein d'un programme destiné à réaliser la modélisation de scènes 3D constitués d'objets auxquels un matériel est attribué.
Proposer une classe et ses attributs permettant de représenter un matériel permettant la gestion de réflexions diffuse, spéculaire et ambiante.
Exercice n°3
On souhaite utiliser les classes développées aux exercices 1 et 2 pour implanter une méthode de calcul de la quantité de lumière diffusée par un matériel sous l'éclairage d'une lumière.
Spécifier cette méthode.
Quelles sont les ajouts à réaliser aux classes des exercices 1 et 2 pour réaliser l'implantation ?
![]()
TP n°5 : Matériel et lumières en OpenGL
Soient les fichiers sources suivants :
- ObjetsGeometriques.h
- ObjetsGeometriques.cpp
- MateriauxEtLumieresBase.cpp
Ces fichiers constituent une application C + GLUt + OpenGL permettant d'afficher quelques scènes simples sans gestion de matériaux et de lumières.
Le but de l'exercice consiste à modifier MateriauxEtLumieresBase.cpp pour y intégrer différentes fonctionnalités d'éclairage et d'attribution de matériaux.
(1) Ajouter les contrôles clavier permettant :
- d'activer/désactiver la gestion des matériaux et lumières (touche F10),
- d'activer/désactiver la lumière 1 (touche F1),
- d'activer/désactiver la lumière 2 (touche F2),
- d'activer/désactiver la lumière 3 (touche F3),
- d'activer/désactiver la lumière 4 (touche F4).
La lumière 0 ne sera pas utilisée.
(2) Modifier le paramétrage de la lumière 1 pour qu'elle devienne une lumière uniquement ambiante d'énergie (0.5,0.5,0.5).
(3) Modifier le paramétrage de la lumière 2 pour qu'elle devienne une lumière uniquement diffuse d'énergie (1.0,0.0,0.0).
(4) Modifier le paramétrage de la lumière 3 pour qu'elle devienne une lumière uniquement spéculaire d'énergie (0.0,1.0,1.0).
Ajuster le matériel des objets pour qu'il réponde à un éclairage spéculaire selon les coefficients de réflexion spéculaire (1.0,1.0,1.0) et une réflectivité "moyenne".
Dans les questions suivantes, les positions et directions spécifiées sont à considérer dans le repère global.
(5) Modifier les paramétrages des lumières 1, 2 et 3 pour qu'elles deviennent respectivement :
- une lumière directionnelle provenant de l'avant gauche pour la lumière 1,
- une lumière directionnelle provenant de l'avant droite pour la lumière 2,
- une lumière ponctuelle placée en position (5.0,5.0,5.0) pour la lumière 3.
(6) Configurer la lumière 4 pour qu'elle devienne un spot blanc et diffus placé en position (-5.0,-5.0,10.0) éclairant vers l'origine du repère avec un angle d'ouverture de 2°.
Ajouter un contrôle clavier permettant d'augmenter/diminuer son ouverture par incrément/décrément de 0.1° entre chaque image.
(7) Tester les animations suivantes :
- La scène tourne sur elle-même et les lumières ne bougent pas.
- La scène et les lumières tournent sur elles-mêmes en même temps.
- La scène ne bouge pas et les lumières tournent autour de la scène.
(8) Jouer sur le paramétrage des matériaux pour que les objets de la scène aient des looks différents :
- La sphère centrale est uniquement diffusante et de couleur rouge.
- Les 8 cubes sont uniquement diffusants dans le jaune et réfléchissants dans le blanc.
- Les 12 "cubes" sont uniquement "ambiants" dans le magenta et réfléchissants dans le cyan.
(9) Modifier la lumière 4 pour qu'elle intégre une décroissance de l'éclairage fonction inverse du carré de la distance (au lieu de sans atténuation). Modifier l'énergie de votre spot pour que la scène redevienne visible.
![]()
TD n°5 : Mathématiques pour l'Informatique Graphique
Exercice n°1
a) Définir une méthode mathématique permettant de calculer la normale d'une facette triangulaire non dégénérée.
b) Définir une méthode mathématique permettant de tester le parallèlisme de deux facettes triangulaires non dégénérées en utilisant uniquement les produit scalaire et produit vectoriel.
c) Définir une méthode mathématique permettant de tester la planarité d'une facette quadrangulaire non dégénérée en utilisant uniquement les produit scalaire et produit vectoriel.
d) Définir une méthode mathématique permettant de tester la convexité du bord d'une facette polygonale plane non dégénérée en utilisant uniquement les produit scalaire et produit vectoriel.
Exercice n°2
L'implantation de l'algorithme de lancer de rayons nécessite de tester l'existence d'intersection(s) entre des rayons lumineux et les objets de la scène.
a) Comment modéliser mathématiquement un rayon lumineux se déplaçant en ligne droite depuis un point d'émission donné et selon une direction donnée.
b) On souhaite tester l'existence d'une intersection entre un rayon lumineux et une sphère caractérisée par son rayon et la position de son centre. Résoudre mathématiquement ce problème.
Exercice n°3
Une courbe 3D est définie par son système d'équations paramétriques. Celles-ci sont des équations polynomiales de degré 3.
a) On souhaite calculer le vecteur vitesse de déplacement sur cette courbe. Comment faire ?
b) On souhaite calculer le vecteur accélération de déplacement sur cette courbe. Comment faire ?
![]()
TP n°6 : Mise en route du projet
Le thème du projet est : Jeu de l'oie.
Dans le cadre de ce thème, le sujet en lui-même est libre. Une validation sera réalisée en amont au cours de la semaine du 3 mars.
Les requis de développement sont les suivants :
- La programmation devra être réalisée en POO en C++. Cet aspect ne pose pas de problème particulier même si OpenGL est une librairie C et même si GLUt est utilisé pour l'interface utilisateur.
Le code obtenu devra être portable (Visual C++ sous Windows et gcc sous Linux).
- Les fonctionnalités de l'informatique graphique qui doivent être utilisées sont :
- modélisation géométrique,
- gestion de lumières,
- gestion de matériaux,
- gestion de textures,
- gestion de caméra avec au moins deux points de vue de visualisation,
- animation du modèle géométrique et/ou de la caméra de visualisation.
Le programme doit inclure des contrôles clavier permettant de :
- switcher entre les points de vue de caméra,
- si adapté à la situation, activer/désactiver/réinitialiser l'animation,
- activer/désactiver les calculs d'illumination,
- activer/désactiver les lumières,
- activer/désactiver le plaçage de texture,
- switcher entre modes d'affichage fil de fer et plein,
- augmenter/diminuer le niveau de facettisation des objets,
- si adapté à la situation, manipuler la scène.
Le contrôle de la vitesse d'animation se fera par contrôle clavier et/ou par synchronisation sur une horloge de l'ordinateur.
L'utilisation de toute IA est interdite.
Le calendrier du projet est :
- définition du sujet : semaine du 3 mars
- rendu d'un prototype/validation de la procédure de rendu : semaine du 7 avril
- rendu définitif : vendredi 9 mai à 18h
Le retour se fera sur moodle dans un dépôt créé à cette fin dans le cours Informatique Graphique de M1. Il consistera en un fichier zip contenant tous les fichiers nécessaires et exclusivement les
fichiers nécessaires :
- fichiers sources (c, cpp, h, hpp),
- fichiers ressources (images, ...),
- fichier readme,
- ...
et n'incluant pas de fichier(s) "gestionnaire de projet". La taille limite pour le fichier zip est 50 Mo. L'archive zip devra s'extraire dans un répertoire créé automatiquement à
cette fin portant dans son nom les noms des 3 membres du groupe.
Le fichier readme (txt ou pdf) contiendra :
- les noms des membres du groupe,
-
une description de la répartition du travail au sein du groupe de travail,
- la liste commentée des fichiers du zip,
- la liste commentée des classes développées,
- une description du sujet,
- une documentation d'utilisation,
- tout commentaire nécessaire à la bonne compréhension de ce qui a été développé.
Un accusé de réception sera envoyé par mail aux adresses indiquées dans le readme lorsque l'archive aura été récupérée et extraite, ou en cas de problème.
![]()
TP n°7 et TP n°8 : Plaçage de texture
OpenGL n'inclut pas de fonction permettant de réaliser l'importation d'une image depuis un fichier.
a) Télécharger l'archive ChargementImagePNG.zip. Cette archive contient les fichiers de code source nécessaires
à la compilation d'une librairie contenant des fonctions d'importation et d'exportation d'images au format PNG 24 bits.
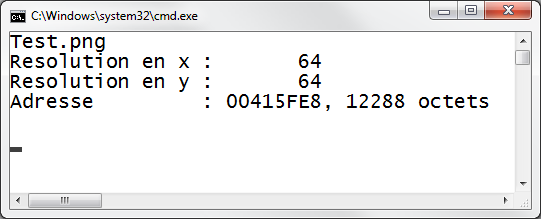
L'utilisation de la fonction d'importation est montrée dans la fonction main du fichier ChargementImagePNG.cpp
qui tente de charger une image. Si le chargement échoue, un message l'indique en disant que l'adresse mémoire du tableau d'unsigned char
obtenu est l'adresse NULL (fréquemment 0x00000000). Si le chargement aboutit, un message l'indique et la résolution de l'image est affichée ainsi
que l'adresse et la taille en octets du tableau d'unsigned char obtenu. Ce programme n'affiche pas l'image. Il se contente de la
télécharger en mémoire. Attention : La fonction d'importation retourne un tableau d'octets aloué dynamiquement, il convient que ce tableau soit libéré après utilisation.
Extraire l'archive, intégrer les fichiers de code source qu'elle contient dans un projet de développement (Visual Studio ou autre), vérifier
la bonne compilation et la bonne exécution du programme. On pourra utiliser les fichiers PNG suivants pour les tests :
Test.png, Bois.png, Emojis.png.
Attention : Seule l'importation de fichiers PNG 24 bits est fonctionnelle. Les fichiers PNG 32 bits ne sont pas correctement importés.
b) Récupérer le fichier de code source TD-PlacageTexture.cpp. Ce fichier contient un exemple
de programme montrant comment OpenGL permet le plaçage d'une texture sur un rectangle ou un cylindre. Dans ce programme l'image est créée
algorithmiquement au moyen de la fonction static unsigned char *image(int nc,int nl) qui crée une image de résolution nc x nl pixels et retourne
cette image sous la forme d'un tableau unidimensionnel d'octets non signés. Le format de ce tableau est RVB entrelacé 24 bits c'est à
dire que chaque pixel est décrit par trois composantes rouge, verte et bleue stockées dans cet ordre et codées individuellement au moyen d'un
octet non signé, et que le fichier contient séquentiellement chaque pixel de l'image dans l'ordre gauche à droite et haut en bas.
Intégrer le code source de la fonction main du fichier ChargementImagePNG.cpp au début de la
fonction main du fichier TD-PlacageTexture.cpp. Vérifier la compilation et l'exécution.
Pour l'instant vous n'utilisez pas l'image pour votre affichage. Ce sera l'objet de la question (c).
c) Remplacer l'image générée algorithmiquement dans le fichier TD-PlacageTexture.cpp par une image obtenue par téléchargement d'un fichier image PNG 24 bits.
d) Reprendre et adapter la fonction de modélisation de cube développée au TP n°4 pour qu'elle permette le placement d'une texture sur chacune
des 6 faces d'un cube.
Cette fonction intégrera donc la modélisation des sommets, des normales, mais aussi des coordonnées de texturage.
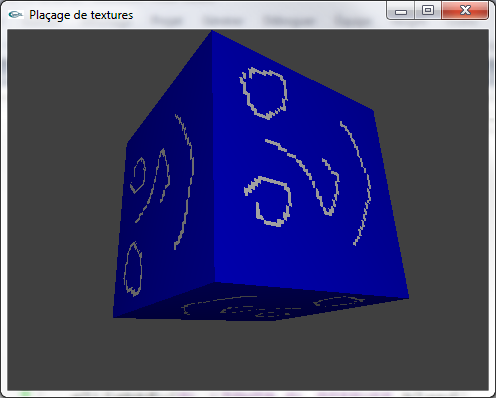
e) Adapter une seconde fois la fonction de modélisation de cube de façon qu'elle réalise le placement de textures différentes sur les 6 faces
du cube.
On pourra utiliser les images suivantes : Emojis.zip.
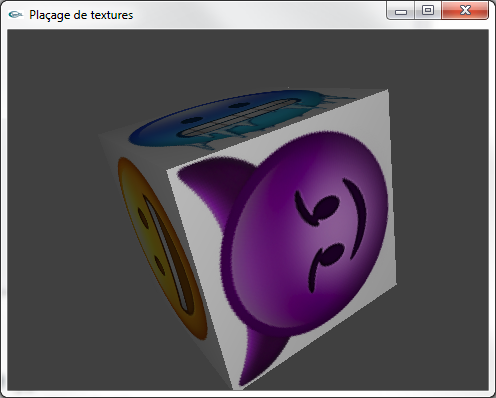
Solutions
|
GLUT |
||
| Placage d'une texture sur un cube | ||
| Placage de 6 textures sur un cube | ||
|
Préload de 6 textures en GPU et placage sur les 6 faces d'un cube |
||
![]()
TD n°6 : Paramètrage numérique d'une caméra OpenGL
a) On considère une caméra de visualisation en projection parallèle orthographique "placée" en position (0.0, 0.0, 0.0) orientée selon l'axe (0.0,
0.0, -1.0). On considère une scène centrée sur le point de coordonnées (0.0, 0.0, -100.0) et occupant un volume sphérique de rayon 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans une fenêtre d'affichage carrée (viewport carré)
?
Définir le paramétrage numérique de la fonction OpenGL utilisée pour réaliser cette visualisation : glOrtho.
b) On considère une caméra de visualisation en projection en perspective placée en position (0.0, 0.0, 0.0) orientée selon l'axe (0.0, 0.0, -1.0).
On considère une scène centrée sur le point de coordonnées (0.0, 0.0, -100.0) et occupant un volume sphérique de rayon 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans une fenêtre d'affichage carrée (viewport carré)
?
Définir le paramétrage numérique de la fonction OpenGL utilisée pour réaliser cette visualisation : gluPerspective.
c) Dans le cadre d'une implantation OpenGL, décrire une solution permettant de s'assurer que l'intégralité de la scène sera visualisée quel que soit le ratio résolution horizontale sur résolution verticale adopté par le viewport d'affichage.
Solutions
![]()
TP n°9 : Paramètrage numérique d'une caméra OpenGL
Le fichier code source ParametrageCamera.cpp contient un programme C + OpenGL complet réalisant
la modélisation géométrique d'une scène et organisant incomplètement son affichage écran. Cette scène est constituée de 64 cubes de coté 0.5
placés en 4 plans de 4 x 4 cubes de façon à occuper un volume cubique de coté 6.5 centré sur le point de coordonnées (0.0,0.0,-100.0). Les cubes sont
colorés en fonction de leur position dans la scène (de plus en plus rouge de gauche à droite, de plus en plus vert de bas en haut, de plus en plus
bleu de l'arrière vers l'avant). L'affichage est incomplètement implanté (fonction ad hoc placées en commentaires) avec pour conséquence
que l'exécution est possible, mais que la scène n'est pas visible.
Télécharger et compiler ce fichier. Vérifier la bonne exécution de l'exécutable ainsi obtenu. Une fenêtre uniformément grise devrait être affichée.
a) Modifier la fonction reshape en décommentant la ligne glOrtho et en paramétrant cet appel de fonction pour visualiser la scène au moyen d'une
caméra réalisant une projection parallèle orthographique, virtuellement placée en position 0.0 et orientée selon l'axe -z.
Rappel : La caméra de visualisation en projection parallèle orthographique d'OpenGL est placée à l'origine et est orientée selon l'axe
-z.
b) Modifier la fonction reshape en recommentant la ligne glOrtho, en décommentant la ligne gluPerspective et en paramétrant cet appel de fonction
pour visualiser la scène au moyen d'une caméra réalisant une projection en perspective, placée en position 0.0 et orientée selon l'axe -z.
Rappel : La caméra de visualisation en projection en perspective d'OpenGL est placée à l'origine et est orientée selon l'axe -z.
c) On souhaite maintenant donner l'illusion que la caméra de visualisation en perspective n'est plus placée à l'origine, mais en position
(0.0,0.0,-50.0).
Décommenter la ligne d'appel à la fonction gluLookAt placée dans la fonction display et paramétrer cet appel pour réaliser cette configuration.
Attention : Il pourra être nécessaire d'ajuster les paramètres d'appel de la fonction gluPerspective pour que la visualisation soit correctement
réalisée.
On se référera à la description de la fonction gluLookAt réalisée dans le chapitre de cours sur OpenGL pour les renseignements d'utilisation.
d) Déplacer de nouveau la caméra vers les positions (0.0,0.0,-90.0) puis (0.0,0.0,-95.0) puis (-5.0,-5.0,-95.0) puis (-10.0,-15.0,-90.0) et enfin (-10.0,-15.0,-120.0).
e) Implanter des contrôles clavier permettant de faire varier la position de la caméra au moyen des touches right et left pour les déplacements en x, up et down pour les déplacements en y, et page up et page down pour les déplacements en z.
Solutions
![]()
Hiérarchie de classes
| Vecteur4 | CH3D | Pos3D | ||||
| Dir3D | ||||||
| Matrice4x4 | TG3D | Tr3D | ||||
| MatriceDeBase | Rt3D | |||||
| Sc3D | ||||||
| LookAt | ||||||
| Rvb | Couleur | |||||
| Energie | ||||||
| Lumiere | LumierePonctuelle | LumiereSpot | ||||
| LumiereDirectionnelle | ||||||
| Materiel | ||||||
| Objet | Sphere | |||||
![]()

