Examen de TD 2003-2004
![]()
Exercice 1: Calculs d'illumination
La réponse à la question (a) devra être justifiée.
- Définir un type de donnée "source lumineuse ponctuelle".
- Spécifier et écrire une fonction calculant l'énergie lumineuse reçue en un point arbitraire depuis une source lumineuse ponctuelle (énergie proportionnelle à l’énergie émise, inversement proportionnelle au carré de la distance).
- Spécifier et écrire une fonction évaluant l'énergie lumineuse diffusée (formule de
Lambert,
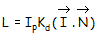 ) en un point d'une surface éclairée par
une source lumineuse ponctuelle. La surface est munie d’un matériel diffusant.
) en un point d'une surface éclairée par
une source lumineuse ponctuelle. La surface est munie d’un matériel diffusant.
Exercice 2: Lancer de rayons
Ecrire une fonction calculant le rayon réfléchi au niveau de
l’interface entre deux milieux. La direction du rayon réfléchi ![]() est calculable par la formule
est calculable par la formule![]() où
où![]() est la normale à l’interface
au point de réflexion et
est la normale à l’interface
au point de réflexion et![]() est le rayon incident.
est le rayon incident.
Exercice 3: Programmation OpenGL
On souhaite programmer une scène animée en OpenGL. Cette scène représente, avec élimination des parties cachées, une sphère affectée d'un matériau diffusant jaune (balle de tennis), de rayon 1, de position initiale (0.0,10.0,0.0) tombant balistiquement selon l'axe -Oy pour rebondir centrée au point (0.0,0.0,0.0), revenir se placer en position initiale et s'immobiliser.
- L'animation est déclenchée par l'appuie de la touche 'A' du clavier.
- L'animation est composée de 1001 images successives numérotées de 0 à 1000 (numéros 0 à 499 à l'allée, 500 au point de rebond, 501 à 1000 au retour)
- La coordonnée y en phase descendante est obtenue par la formule
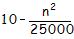 où n désigne le numéro de l'image. La coordonnée y en phase montante
est
où n désigne le numéro de l'image. La coordonnée y en phase montante
est  .
.
- Ecrire la fonction init.
- Ecrire la fonction idle.
- Ecrire la fonction key.
- Ecrire la fonction display.
Exercice 4: Algorithmique
Programmer la généralisation à un espace trois dimensions et 26-connexité de l’algorithme de Bresenham pour le dessin de segments dans un espace bitmap (deux dimensions et 8-connexité).
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr