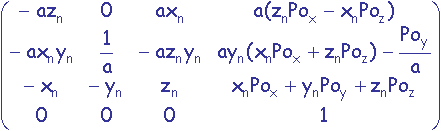
a) Produit de matrices canoniques

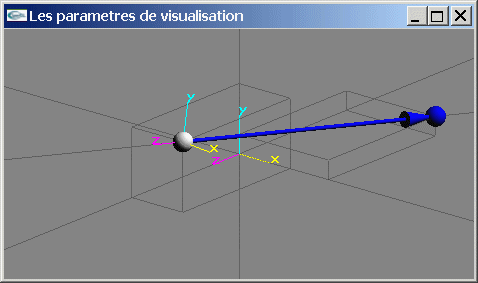
Point de vue souhaité
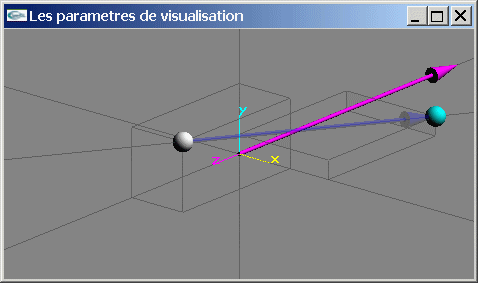
Point de vue assuré par le repère initial
Trois transformations géométriques doivent être réalisées successivement:
Transformation 1: Une translation pour déplacer l'origine du repère vers le point Po.
Il s'agit d'une translation de vecteur ![]() (qu'on peut aussi noter
(qu'on peut aussi noter ![]() ). Elle est notée T.
). Elle est notée T.
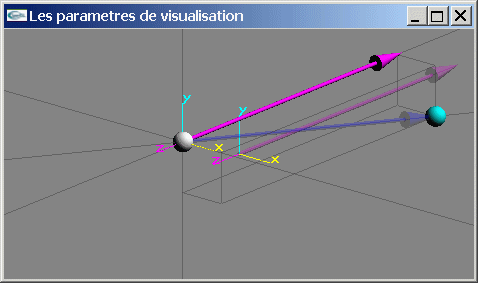
Après la transformation T
Transformation 2: Une rotation d'angle qy autour de l'axe Oy pour déplacer le point Pv dans le demi plan yOz de z négatif. Ce mouvement revient à "tourner la tête". Elle est notée R1.
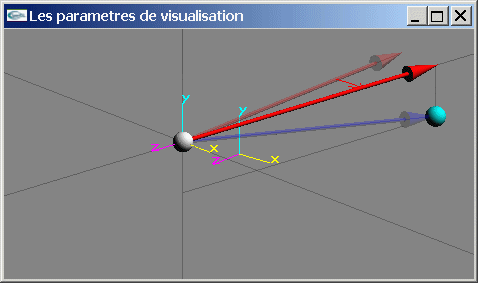
Après la transformation R1
Transformation 3: Une rotation d'angle qx autour de l'axe Ox pour déplacer le point Pv sur l'axe -Oz. Ce mouvement revient à "monter/baisser la tête". On la note R2.
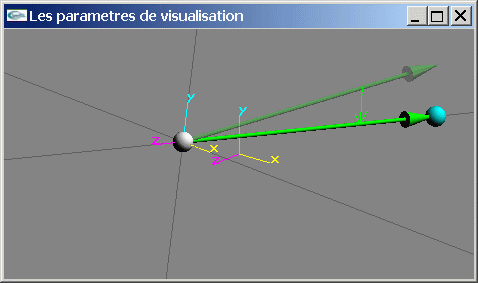
Après la transformation R2

Point de vue final
La transformation géométrique résultante est donc M = R2.R1.T.
Calcul de qy et qx
Si on connait le vecteur ![]() =
=
![]() .
.
On établit que qy = -atan2(-vx,-vz) qui définit R1.
Si on multiplie R1 par ![]() , on
obtient le vecteur
, on
obtient le vecteur ![]() .
.
On établit alors que qx = atan2(-vy',-vz') qui définit R2.
Si on multiplie R2 par ![]() , on obtient le vecteur
, on obtient le vecteur 
qui vérifie vz" = distance(Po,Pv).
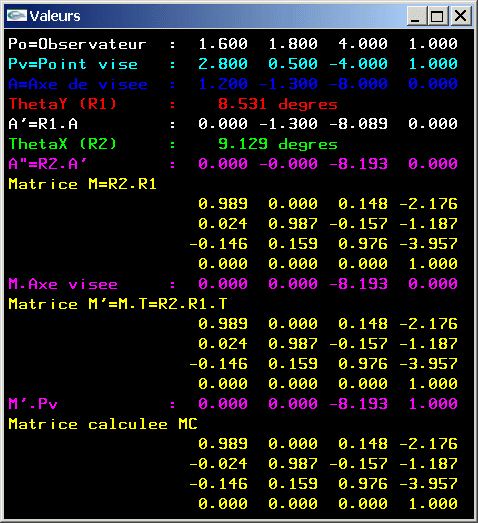
Paramètres numériques de visualisation
b) Résultat du produit matriciel
T = 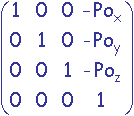
R1 = 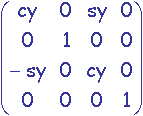
R2 = 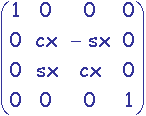
M = R2.R1.T = 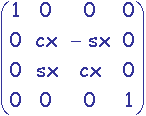 .
.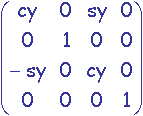 .
.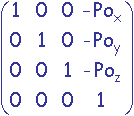
M = 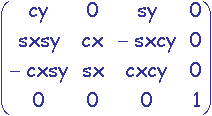 .
.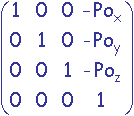
M = 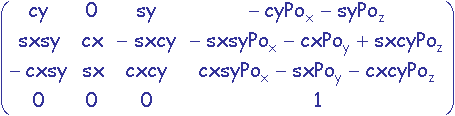
c) Verticales?
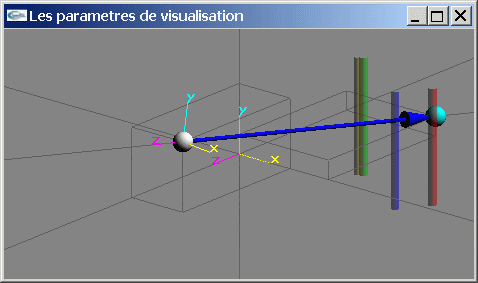
Point de vue sur une scène constituée de cylindres verticaux
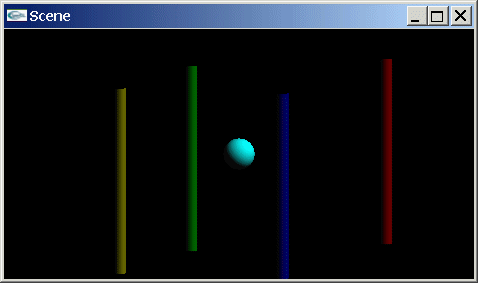
Image obtenue
La verticale du repère global est l'axe des y.
M.![]() =
= 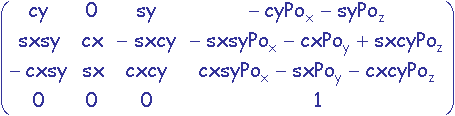 .
.![]() =
= ![]()
Ce vecteur est caractérisé par une coordonnée en x égale à 0
-> il apparaîtra vertical à l'observateur.
d) Simplication
Dans le repère de l'observateur le vecteur normé de même direction que ![]() à pour coordonnées (0,0,-1).
Multiplié par la matrice M-1 , ce vecteur est obtenu dans le repère global.
à pour coordonnées (0,0,-1).
Multiplié par la matrice M-1 , ce vecteur est obtenu dans le repère global.
M-1 = T-1.R1-1.R2-1
M-1 = 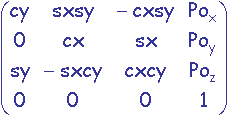
M-1.![]() =
= 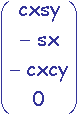 =
= ![]()
-> cxsy = -xn
-> sx = -yn
-> cxcy = -zn
-> cx = ![]()
Si on pose a = 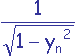
->cy = -azn
-> sy = axn
par subsitutions, M =