L'algorithme du Z-Buffer est un algorithme d'élimination des parties
cachées.
-> Lors de la visualisation d'une scène, cet algorithme supprime l'affichage de tout
objet ou morceau d'objet masqué par un autre objet ou par lui même.
Algorithme conçu au milieu des années 70.
Autres algorithmes d'élimination des parties cachées:
- algorithme du peintre,
- algorithmes de la ligne de balayage (scanline),
- algorithmes par subdivision de l'image (Warnock, ...),
- ...
|
|||||||
Principe du Z-Buffer
Le calcul de l’image est effectué séquentiellement en traitant les
objets extraits de la scène (classiquement des facettes triangulaires) les uns à la
suite des autres pour en extraire l'intégralité des pixels qui les représentent.
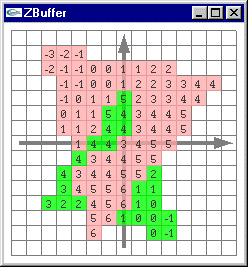
Au cours du processus de traitement d'un objet, chaque pixel calculé voit sa
"profondeur" comparée à celle déjà calculée en cette position image pour
pouvoir afficher finalement la facette la moins "profonde" présente en cette
position (vis à vis de l'observateur).
-> Il n'y a pas de tri des objets, mais un calcul de maximum, pour chaque pixel de l'image, vis à vis de l'ensemble des objets présents en ce pixel.
Ne pas réaliser la séquentialisation sur les pixels mais sur les objets a beaucoup d'intérêts:
- optimisation des calculs,
- algorithme en temps linéaire du nombre de facettes,
- possibilité de commencer le calcul de l'image sans connaître l'intégralité de la scène,
- ...
On définit deux zones mémoire de tailles identiques à la taille de l'image que l'on souhaite calculer:
un tampon couleur destiné à contenir la couleur de chacun des pixels de l'image (initialisé à la couleur de fond souhaitée),
un tampon profondeur destiné à contenir la profondeur écran maximum de chacun des pixels de l'image (initialisée à -¥, utilisée comme valeur courante de comparaison en cours d'exécution du Z-Buffer).
La scène est disponible en coordonnées image (coordonnées écran).
On décompose (rasterise) chaque surface s à afficher en l'ensemble des pixels de coordonnées (x,y) qui la composeraient si elle était intégralement affichée seule.
Au cours de la décomposition, on calcule la profondeur écran z de chaque pixel de s de coordonnées image (x,y).
Si cette coordonnée est plus grande que celle déjà présente dans le tampon profondeur aux coordonnées (x,y), la nouvelle profondeur en (x,y) devient z et la couleur du pixel (x,y) du tampon couleur est réaffectée avec une valeur calculée en fonction de x, de y, des caractéristiques de la surface s, de sources lumineuses, ...
Quand toutes les surfaces ont été traitées, l'image est disponible dans le tampon couleur pour être affichée à l'écran.
Initialiser le
tableau PROF à -¥
Initialiser de tableau COUL
à la couleur de fond
Pour chaque objet o de la scène à représenter
Pour chaque pixel p=(x,y) de o
Calculer la profondeur z de p=(x,y) ;
Si z > PROF(x,y) alors
PROF(x,y) = z ;
COUL(x,y) = couleur(o,x,y) ;
Finsi
Finpour
Finpour
Pour ce type d'objet, le calcul de la profondeur écran nécessaire à la rastérisation se marie bien avec l'opération de remplissage et entraîne donc un surcoût de calcul peu important.
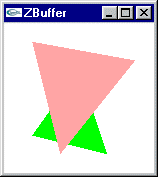
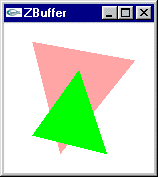
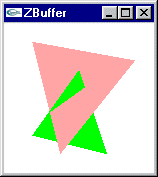
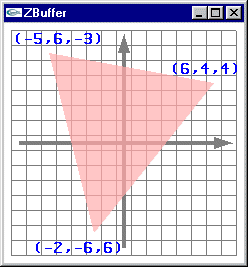
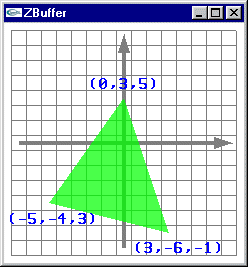
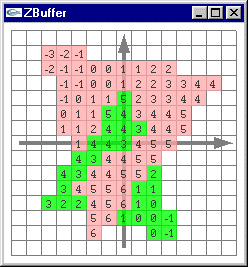
2 facettes à afficher
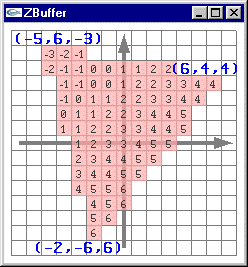
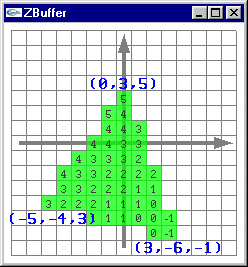
Rasterisation de chacune de ces facettes
Calcul d’altitude pour chacun des pixels
|
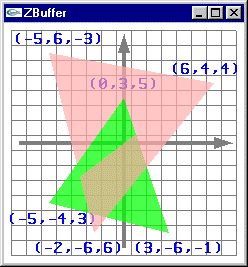
On dispose de facettes triangulaires dont les sommets sont connus en coordonnées écran.
Problèmes:
- Établir quels sont les pixels recouvrant chacune des facettes : Remplissage 2D.
- Calculer l'altitude de chacun de ces pixels.
Solution au premier problème: Trouver les pixels sur les cotés droit et gauche de la facette traitée. Tracer la trame horizontale entre le couple de pixels de chaque ligne de pixels sur laquelle la facette apparaît.
Solution au second problème: Travailler le remplissage 2D en gérant z en paramètre supplémentaire (pour optimiser les calculs, mariage de la gestion de z avec l'algorithme de remplissage 2D).
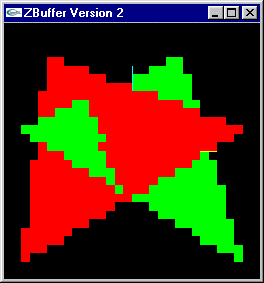
Problème 1 : Remplissage d'une facette 2D |
|
|
|
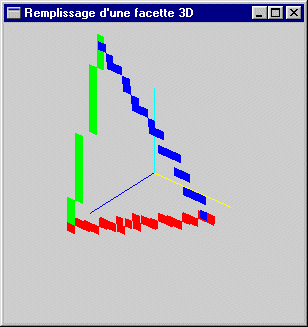
Problème 2 : Remplissage d'une facette 3D |
|
|
|
Différentes unités de mesure de performance:
- taux de génération de pixels (pixels/seconde),
- segments/seconde,
- polygones/seconde.
Sur PC, de quelques dizaines de millions à plusieurs milliards de pixels par seconde, de quelques dizaines de milliers à plusieurs dizaines de millions de polygones par seconde (de quelques dizaines d'€ à plusieurs milliers d'€).
En constante évolution.
Intérêt
Algorithme facilement implantable.
Algorithme pouvant être optimisé (utilisation exclusive d'entiers, utilisation de variantes de l'algorithme de Bresenham pour le tracé de segments).
Algorithme facilement implantable hard.
Algorithme facilement pipelinable et parallélisable.
Compatible de manière simple avec le calcul d'illumination de Gouraud et le placage de texture.
Gestion implicite des recoupements entre objets.
Exécution en un temps en o(n) du nombre de facettes -> bonne scalabilité.
Inconvénients
Les deux zones tampon peuvent avoir des tailles très importantes (plusieurs Mo dans le cas de grands écrans). Actuellement, ce n'est plus véritablement un problème.
La décomposition de chaque surface élémentaire en pixels nécessite une puissance de calcul importante (de l'ordre de 50 Mips pour 100000 facettes/s) et une vitesse d'accès mémoire très élevée (mémoire spécifique -> plus chère).
Des techniques incrémentales (Bresenham) permettent toutefois d'optimiser les performances par l'utilisation de variables entières et d'opérations simples (additions et comparaisons).Pas de gestion intrinsèque simple des phénomènes de réflexion spéculaire et de transmission.
Pas de gestion implicite des ombres portées.
-> Difficultés pour implanter la modélisation de phénomènes optiques complexes.
-> Algorithme standard pour l'obtention en temps réel d'images de qualité moyenne.
-> Application à la conception et fabrication assistée par ordinateur (station de travail graphique), à la réalité virtuelle et au jeu.