Annexes
Annexe 1
DUNE et SYMON : logiciels pour la synthèse d'images de paysages Les fonctionnalités décrites dans cette thèse ont été implantées au sein de deux logiciels de modélisation et de dessin DUNE (cf [JA89], [AJ90b,c]) et SYMON qui permettent la création des structures topologiques et géométriques des arbres et des reliefs modélisés ainsi que leurs dessins.A1.1 Introduction
Dans l'implantation actuelle, DUNE et SYMON fonctionnent sur tout matériel compatible IBM/PC sous le système d'exploitation MS-DOS. La qualité des dessins obtenus est bien entendu fonction de la qualité de l'écran graphique utilisé. Toutes les photographies ci-incluses ont été réalisées sur une machine équipée d'une carte IBM 8514A (résolution de 1024 par 768 points avec 256 couleurs parmi 256K, 64 niveaux de gris). Les performances de cette carte sont moyennes tant en qualité graphique qu'en vitesse d'affichage.
A1.2 DUNE : Génération et dessin d'arbres
A1.2.1 Génération et dessin d'arbres : MENU ARBRE
A1.2.1.1 Génération de la topologie d'un arbre
La topologie d'un arbre binaire peut être construite à partir des données suivantes correspondant deux modèles topologiques de génération développés aux chapitres 3 et 4.
par matrice de ramification :
- une matrice de ramification stockée préalablement dans un fichier,
- l'ordre de l'arête initiale de l'arbre topologique binaire généré (de 2 à 15 dans la majorité des cas),
- la dimension maximale que pourra adopter l'arbre généré (de 1 à 32000 nœuds internes).
par matrice d'évolution :
- l'âge maximum A de la suite d'arbres à générer,
- une sous-matrice d'évolution stockée préalablement sur disque,
- un nom sur quatre caractères qui sera la partie commune de tous les noms de fichiers dans lesquels seront stockés les arbres intermédiaires,
- la dimension maximale que pourra avoir l'arbre généré (de 1 à 32000 nœuds internes).
L'évolution des arbres topologiques selon la sous-matrice fournie se poursuit génération après génération jusqu'à ce que l'âge maximum soit atteint ou que la taille maximale soit dépassée ou qu'il n'y ait plus de lignes dans la sous-matrice.
Un certain nombre d'autres modèles de génération topologique sont disponibles (Figure A1A).
A1.2.1.2 Plongement géométrique
La géométrie de l'arbre est calculée automatiquement après la génération de la structure topologique en fonction de paramètres prédéfinis. Il convient de paramètrer les lois géométriques pour obtenir l'aspect voulu (coefficients d'angles, lois et coefficients de longueur et épaisseur des branches, choix d'une géométrie 2D ou 3D, ...) (Figures A1A et A1B).
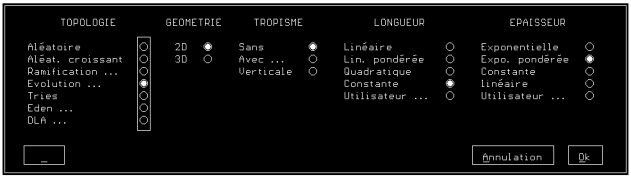
Figure A1A : Paramétrage des modèles de génération topologique et géométrique d'un arbre
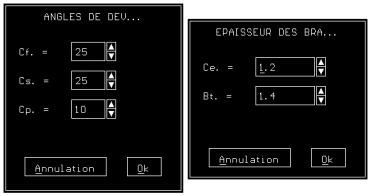
Figure A1B : Paramétrage des coefficients numériques des lois géométrique des arbres
A1.2.1.3 Dessin de l'arbre
Le dessin d'un arbre ne peut s'effectuer sans avoir fixé les options de dessin. Au nombre de celles-ci on trouve (Figure A1C) :
- Taille et position de l'arbre à l'écran.
- Le choix des couleurs et leur nombre.
- La présence d'une texture pour l'écorce.
- Un éventuel effet du vent ou un phototropisme.
- Le type de feuilles à employer (voir paragraphe A1.3), leurs couleurs et leur densité en fonction de l'ordre de chaque branche (Figure A1D).
- La position du soleil dans le cas d'un dessin 3D (Photographie A1A).
- Choix d'une présence ou non d'ombres portées dans l'arbre.
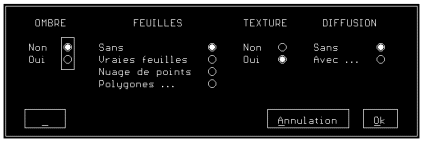
Figure A1C : Différents types de dessins
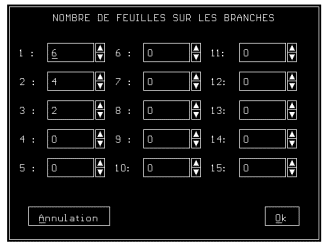
Figure A1D : Nombre de feuilles par branches en fonction de leurs ordres de Strahler
A1.2.2 Génération de feuilles : MENU FEUILLE.
La génération d'une feuille à placer sur un arbre suit le même mode opératoire que la génération d'un arbre :
- Une structure topologique est générée en donnant le nombre de lobes de la feuille à construire, puis la dimension du lobe principal central (cette dimension est mesurée par le nombre de nœuds présents sur la nervure) (Figure A1E).
- La géométrie de la feuille est calculée automatiquement par attribution d'une position aux extrémités de toutes les nervures topologiques. A cette fin DUNE utilise des angles paramètrables ainsi que des lois de calcul des longueurs des arêtes dont le type est lui aussi paramètrable. Ces lois peuvent de plus être paramétrées au moyen de coefficients numériques. Des variations aléatoires peuvent être ajoutées (décrochements au niveau des nœuds de nervures principales) (Figure A1E).
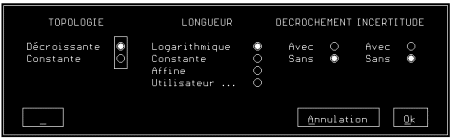
Figure A1E : Paramétrage des modèles de génération topologique et géométrique d'une feuille
Une fois les structures topologiques et géométriques générées, le dessin de la feuille peut être effectué avec bord lissé ou non lissé. Dans le premier cas le dessin est rapide mais peu soigné et suffit dans le cas de feuilles vues de loin. Dans le second cas on obtient une bonne qualité de dessin au détriment bien sûr de la rapidité.
Il est possible de dessiner les feuilles avec un dégradé de couleurs, ces couleurs étant choisies en fonction de la distance à la nervure principale. Avant d'utiliser une feuille pour le dessin d'un arbre, il convient d'adapter sa taille écran vis à vis de la taille de l'arbre.
Dans le cas du dessin d'un arbre muni d'un feuillage, pour une prévisualisation rapide, DUNE permet de simplifier la modélisation des feuilles en substituant à de vraies feuilles une représentation purement polygonale ou bien encore plus simplement des nuages de points. Ceci est particulièrement appréciable lors du dessin d'un arbre composé de plusieurs milliers de branches, et nécessitant alors plusieurs milliers de feuilles. Ce type de rendu peut éventuellement être utilisé pour des arbres vus de loin, car le résultat reste visuellement acceptable et le temps de dessin est réduit
A1.3 SYMON : Génération de paysages
La génération d'un relief est liée à l'utilisation d'un arbre topologique déjà présent en mémoire (voir paragraphe A1.2.1.1, fonctionnalité de DUNE également disponible sous SYMON). Classiquement la taille de cet arbre varie d'une dizaine à quelques dizaines de nœuds internes. A partir de cet arbre, SYMON génère une carte planaire quasi-triangulaire topologique qui est ensuite plongée automatiquement dans
R3 suivant le modèle du chapitre 6. Le niveau de modélisation topologique (avec ou sans lignes de crête, avec fractalisations supplémentaires locales ou globales éventuelles), les lois utilisées au cours du plongement géométrique ainsi que leurs coefficients numériques sont paramétrables (Figure A1F).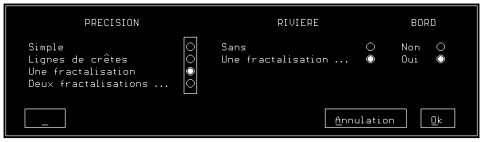
Figure A1F : Option de génération de la topologie d'un relief
La taille de la carte obtenue est limitée structurellement dans l'implantation actuelle par le nombre de brins qu'elle contient qui ne peut pas dépasser 65536, c'est à dire qu'il ne peut pas y avoir plus de 32768 arêtes.
Pour réaliser le dessin de cette carte, qui est maintenant devenue un relief, on doit choisir entre un mode de représentation en deux dimensions projetées ou une vue en perspective. Dans ce dernier cas, on fixe la position virtuelle du viseur ainsi que la direction de visée (avec un paramètrage éventuel de la focale de l'objectif utilisé). Il reste enfin à définir les différentes options de dessin (Figure A1G) :
- Le type de rendu (par facette ou avec lissage de Gouraud).
- La matérialisation ou non des lignes de crête lors du lissage de Gouraud.
- La présence ou non de strates de couleurs en fonction de l'altitude.
- Le choix des couleurs et leur nombre.
- La position du soleil (Photographie A1A).
- L'inclusion ou non d'arbres dans le relief (par désignation d'un fichier contenant les informations nécessaires à leur gestion).
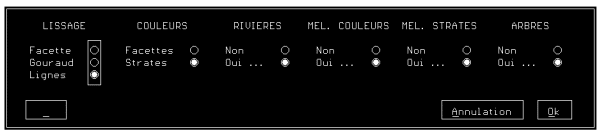
Figure A1G : Options de dessin d'un relief
A1.4 Performances
Les temps de dessin fournis ci-après ont été mesurés sur un IBM PS/2 8580 dont les caractéristiques techniques sont les suivantes :
- processeur 80386DX à 16 Mhz,
- coprocesseur arithmétique 80387DX à 16 Mhz,
- Disque dur 40 Mo (38 ms de temps d'accès, 500 Ko / s de vitesse de transfert),
- carte graphique IBM 8514A (1024 * 768 * 256, 64 niveaux de gris),
- écran graphique 8514.
Les temps obtenus pour la génération et le dessin des arbres sont :
- de l'ordre de la dizaine de secondes pour la génération par matrice de ramification ou d'évolution de la topologie et de la géométrie 3D d'un arbre de quelques milliers de nœuds internes (sauvegarde sur disque de tous les arbres intermédiaires dans le cas de l'utilisation d'une matrice d'évolution),
- de l'ordre de la minute pour le dessin en 2D de cet arbre avec feuilles polygonales,
- de l'ordre d'une dizaine de minutes pour le dessin en 3D sans feuille.
Le dessin de vraies feuilles à l'échelle sur cet arbre entraîne un délai supplémentaire de l'ordre d'une dizaine de minutes (temps donné pour un arbre de 1000 nœuds internes et donc comportant quelques milliers de feuilles à 3 lobes, 3 nœuds par lobes et 3 couleurs).
Un Z-Buffer initial de calcul des ombres portées demande de quelques secondes à quelques dizaines de secondes, le temps d'affichage de l'arbre n'est ensuite que marginalement modifié.
Pour un relief, les temps sont :
- inférieur à la minute pour la génération d'une carte topologique quasi-triangulaire plongée dans
R3 à partir d'une arborescence binaire topologique de 50 nœuds internes permettant d'obtenir une carte contenant quelques milliers de facettes après création des lignes de crête et une fractalisation sur les rivières,. de l'ordre de quelques dizaines de secondes pour le dessin simple de cette carte sans lissage de Gouraud, sans affichage des rivières, des lignes de crêtes et de strates de couleurs,
- de l'ordre de quelques minutes si l'on ajoute le lissage de Gouraud et l'affichage des rivières, des lignes de crêtes et des strates de couleurs,
- de quelques minutes à quelques dizaines de minutes, si des arbres sont inclus (leur nombre peut varier jusqu'à plusieurs milliers, utilisation d'images présentes sur disque déjà calculées (temps non comptabilisé)),
- voisin d'une dizaine d'heures pour la réalisation d'une animation sur cette carte avec 2000 arbres permettant de calculer quelques centaines d'images (la taille de ces images est volontairement limitée à quelques centaines de points en x et en y, habituellement 300 x 225, pour accélérer le calcul, diminuer le volume de stockage des images, et rendre l'animation plus coulée et plus rapide).
A1.5 Fonctionnalités avancées
Outre celles abordées dans les paragraphes précédents les principales fonctionnalités quant à l'utilisation de DUNE et SYMON sont les suivantes :
- Utilisation d'une interface interactive au moyen de fenêtres et de la souris (fonctionnalité impérative pour un travail facile et rapide).
- Affichage à l'écran d'informations textuelles :
- Extraction de matrices à partir d'arbres topologiques importés.
- Calculs de valeurs d'ordre statistique (longueurs moyennes des segments des arborescences topologiques, longueurs moyennes des arêtes des cartes, surface moyenne des facettes des cartes, ...).
- Travail sur les matrices :
- Editeur de matrice.
- Composition de combinaisons linéaires entre matrices.
- Composition de mélanges de matrices: une matrice peut être construite à partir de lignes extraites d'autres matrices.
- Taille théorique des arbres générés.
- Gestion d'un outil de construction de fichiers paysage (Photographie A1B).
- Gestion d'un outils de définition d'une trajectoire à l'intérieur d'un relief (Photographie A1C) et de dessin automatique d'un nombre paramétrable de vues le long de cette trajectoire (Figure A1H).
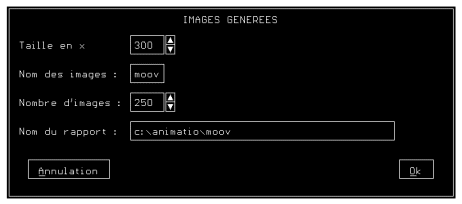
Figure A1H : Génération d'une animation à partir d'un relief.
- Gestion de la palette de couleur (Photographie A1D).
-Possibilités de manipulation d'images bitmap (zoom, Photographie A1E, sélection d'une partie, copier-coller,…).
- Gestion d'un éditeur.
- Gestion d'outils de type PAINT.
- Sauvegarde d'images.
Photographie A1A : Paramètrage de la direction d'éclairage.
Photographie A1B : Création dynamique d'un fichier paysage.
Photographie A1C : Construction dynamique d'une trajectoire à l'intérieur d'un relief
Photographie A1D : Gestion de la palette de couleur
Photographie A1E : Gestion d'une fenêtre "zoom" sur une portion de l'image
Annexe 2
Particularités des structures de donnéesL'efficacité et la facilité d'implantation des modèles définis dans les travaux présentés dépendent grandement des structures de données utilisées. Les paragraphes 2.2.4 et 2.3.2 en donnent des exemples. Toutefois, compte tenu des opérations que nous désirons réaliser sur ces objets topologiques ces structures peuvent être simplifiées pour une plus grande facilité d'utilisation.
A2.1 Les arbres binaires
La structure de donnée de base est
STRUCT NŒUD {
STRUCT NŒUD *FILS_DROIT ;
STRUCT NŒUD *FILS_GAUCHE ; }
où à chaque nœud de la structure est associé de manière évidente un pointeur sur son fils droit et un pointeur sur son fils gauche. Or pour générer un arbre par une matrice de ramification ou une matrice d'évolution, une taille maximale est fixée a priori. Plutôt que d'utiliser une représentation par pointeurs lourde en temps de calcul et peu économique en mémoire, on préférera une représentation par tableau où au lieu de gérer des pointeurs sur les fils droit et gauche on donnera l'indice de ces fils. Ce choix est possible dans la mesure où les opérations que nous avons à réaliser sur les arbres ne sont pas du type "chirurgicale" (c'est-à-dire partage en sous-arbres, suppression de nœuds, de sous-arbres,…).
On aura donc :
STRUCT NŒUD {
UNSIGNED FILS_DROIT ;
UNSIGNED FILS_GAUCHE ; }
Si les indices des fils droit et fils gauche d'un nœud n sont égaux à zéro alors ce nœud sera terminal. Un certain nombre de champs supplémentaires sont nécessaires à l'utilisation des matrices de ramification et d'évolution pour la génération d'arborescences binaires :
STRUCT NŒUD {
UNSIGNED ORDRE_STRAHLER ;
UNSIGNED ORDRE_EVOLUTION ;
UNSIGNED FILS_DROIT ;
UNSIGNED FILS_GAUCHE ; }
Enfin pour utiliser un arbre comme structure de base de génération d'un relief, un dernier champ est nécessaire pour associer tout nœud de l'arborescence au nœud correspondant de la carte. Ce champ est aussi de type unsigned car, comme on le verra, l'utilisation de tableaux d'indices est aussi possible pour le stockage des cartes représentant les reliefs. On a donc :
STRUCT NŒUD {
UNSIGNED ORDRE_STRAHLER ;
UNSIGNED ORDRE_EVOLUTION ;
UNSIGNED FILS_DROIT ;
UNSIGNED FILS_GAUCHE ; }
UNSIGNED NOEUD_DANS_CARTE ; }
A2.2 Les cartes planaires
A2.2.1 Structure de données
Les cartes planaires peuvent être stockées au moyen de la structure de données suivante (représentation par premier successeur et file des successeurs sur chaque nœud avec existence d'une face extérieure) :
STRUCT SOMMET {
STRUCT SOMMET * SOMMET_SUIVANT;
BOOLEAN BORD_EXTERIEUR ;
STRUCT SUCCESSEUR *PREMIER_SUCCESSEUR ; }
STRUCT SUCCESSEUR {
STRUCT SOMMET *SOMMET_ARETE ;
STRUCT SUCCESSEUR *SUC_SUIVANT;
STRUCT SUCCESSEUR *SUC_PRECEDENT ;
STRUCT SUCCESSEUR *BRIN_OPPOSE ;}
De la même manière que pour les arbres et compte tenu du fait que les seules opérations effectuées sur les cartes sont des opérations de construction en connaissant a priori la taille finale de la structure générée (voir paragraphe A2.2.2) et non pas de destruction (suppression de sommets et/ou d'arêtes, partage en sous-cartes), il est possible de modifier cette structure de donnée pour gérer des indices dans des tableaux et non plus des pointeurs.
On aura donc :
STRUCT SOMMET {
BOOLEAN BORD_EXTERIEUR ;
UNSIGNED PREMIER_SUCCESSEUR ; }
STRUCT SUCCESSEUR {
UNSIGNED SOMMET_ARETE ;
UNSIGNED SUC_SUIVANT ;
UNSIGNED SUC_PRECEDENT ;
UNSIGNED BRIN_OPPOSE ;}
où l'indice SOMMET_ARETE correspond à un indice du tableau des sommets et les indices PREMIER_SUCCESSEUR, SUC_SUIVANT, SUC_PRECEDENT et BRIN_OPPOSE à des indices du tableau des successeurs (des brins). On remarque la suppression du champ SOMMET_SUIVANT qui n'est plus nécessaire pour chaîner tous les sommets d'une carte, ces sommets étant implicitement dans un tableau.
La génération des cartes matérialisant les reliefs demande la gestion d'un certain nombre d'informations supplémentaires : il faut pouvoir déterminer :
- si un nœud fait partie d'une rivière, d'une ligne de crête ou est simplement issu d'une triangularisation ou de la création d'un bord de facettes verticales,
- si une arête est une rivière, une ligne de crête ou simplement une arête de triangularisation ou de création d'un bord de facettes verticales.
Des champs supplémentaires de définition de type vont être gérés :
STRUCT SOMMET {
BOOLEAN BORD_EXTERIEUR ;
INT TYPE ;
UNSIGNED PREMIER_SUCCESSEUR ; }
STRUCT SUCCESSEUR {
INT TYPE ;
UNSIGNED SOMMET_ARETE ;
UNSIGNED SUC_SUIVANT ;
UNSIGNED SUC_PRECEDENT ;
UNSIGNED BRIN_OPPOSE ;}
A2.2.2 Taille d'une carte
L'utilisation de tableaux à la place de zones mémoires pointées nécessite la connaissance préalable à la création des structures de la taille de ces structures. En l'occurrence, on doit ici connaître le nombre de sommets et le nombre de brins de la carte. Les informations connues au départ sont le nombre de nœuds internes de l'arbre source ainsi que le niveau de modélisation topologique que l'on désire atteindre, dans l'ordre chronologique des opérations :
- carte avec ou sans lignes de crête,
- fractalisation globale,
- fractalisation sur les rivières,
- création d'un bord vertical sur la carte.
Ces paramètres suffisent à déterminer très exactement le nombre de nœuds et de brins de la carte finale. En effet, si l'arbre initial possède n nœuds internes, la carte topologique la plus simple générée (sans ligne de crête) possède :
- 2*n+2 sommets (y compris le nœud supplémentaire ajouté en aval de la racine de l'arbre binaire),
- 5*n+1 arêtes (évident par le paragraphe 6.2.2 : pour chaque nœud interne de l'arbre binaire sont créées 5 arêtes et 3 facettes triangulaires dans la carte planaire quasi-triangulaire recouvrante. A ces 5*n arêtes, il faut ajouter l'arête supplémentaire aboutissant à la racine), et donc :
- 10*n+2 brins,
- 3*n facettes triangulaires (sans compter la face extérieure),
- n+2 sommets sur le bord (n+1 feuilles de l'arbre recouvrant plus le sommet ajouté en aval de la racine),
- 2*n+1 arêtes rivières et 3*n arêtes non rivières.
La table A2A montre l'évolution de ces tailles si des lignes de crête sont créées (Le détail des calculs n'est pas présenté. Il se réalise de la même façon que précédemment, en analysant les opérations géométriques effectuées au paragraphe 6.2.4).
nœuds |
arêtes |
brins |
facettes |
nœuds sur le bord |
arêtes rivières |
arêtes non rivières |
|
Sans lignes de crête |
2*n+2 |
5*n+1 |
10*n+2 |
3*n |
n+2 |
2*n+1 |
3*n |
Avec lignes de crête |
5*n+2 |
13*n-1 |
26*n-2 |
8*n-2 |
2*n+4 |
2*n+1 |
11*n-2 |
Table A2A : Evolution de la taille d'une carte lors de la création des lignes de crête.
Les modifications de la taille finale de la carte dues aux opérations topologiques supplémentaires s'expriment simplement en fonction des valeurs des nombres de nœuds, de brins, de facettes, de nœuds sur le bord de la carte, d'arêtes rivières et d'arêtes ne représentant pas de rivière.
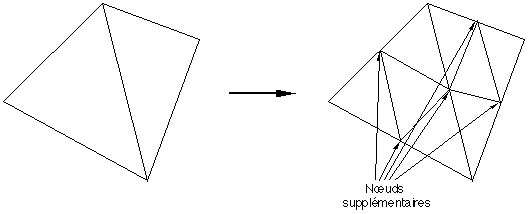
Figure A2A : Fractalisation globale
A chaque nouvelle retriangularisation globale le nombre de nœuds augmente du nombre total d'arêtes présentes dans la carte (avant la retriangularisation), le nombre d'arêtes est augmenté du nombre d'arêtes et de trois fois le nombre de facettes, le nombre de facettes est multiplié par quatre, le nombre de nœuds sur le bord de la carte est multiplié par deux, ainsi que le nombre d'arêtes rivières enfin le nombre d'arêtes non rivière est multiplié par deux et augmenté de trois fois le nombre de facettes (cf figure A2A pour la justification de ces formules et la Table A2B pour leur présentation).
nœuds |
arêtes |
brins |
facettes |
nœuds sur le bord |
arêtes rivières |
arêtes non rivières |
|
Carte initiale |
n |
a |
2*a |
f |
nb |
nr |
ns = a - nr |
Carte après retriangularisation globale |
n+a |
2*a+3*f |
4*a+6*f |
4*f |
2*nb |
2*nr |
2*ns+3*f |
Table A2B : Evolution de la taille d'une carte lors d'une triangulation globale.
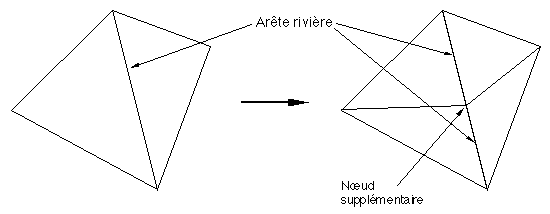
Figure A2B : Fractalisation sur les rivières
A chaque retriangularisation sur les rivières le nombre de nœuds augmente du nombre d'arêtes rivières présentes dans la carte, le nombre d'arêtes est augmenté de trois fois le nombre d'arêtes rivières, le nom de facettes est augmenté de deux fois le nombre d'arêtes rivières, le nombre de nœuds sur le bord de la carte est inchangé, le nombre d'arêtes non rivière est augmenté de deux fois le nombre d'arêtes rivières, le nombre d'arêtes rivières est multiplié par deux (cf figure A2B pour la justification de ces formules et Table A2C pour leur présentation).
nœuds |
arêtes |
brins |
facettes |
nœuds sur le bord |
arêtes rivières |
arêtes non rivières |
|
Carte initiale |
n |
a |
2*a |
f |
nb |
nr |
ns |
Carte après triangularisation sur les rivières |
n+nr |
a+3*nr |
2*a+6*nr |
f+2*nr |
nb |
2*nr |
ns+2*nr |
Table A2C : Evolution de la taille d'une carte lors d'une fractalisation sur les rivières.
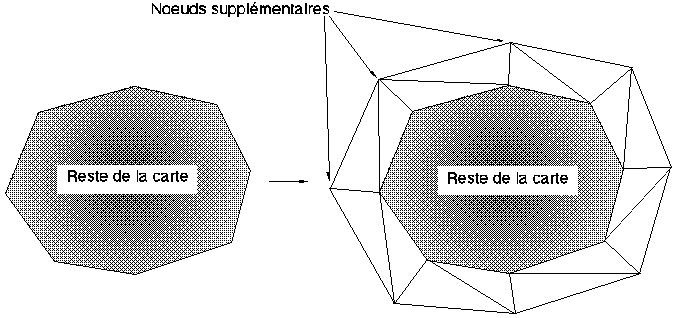
Figure A2C : Création d'un bord de nœuds
Enfin, lors de la création éventuelle d'un bord par ajout de facettes, le nombre de nœuds augmente du nombre de nœuds sur le bord, le nombre d'arêtes augmente de trois fois le nombre de nœuds sur le bord, le nombre de facettes augmente de deux fois le nombre de nœuds sur le bord, le nombre de nœuds sur le bord et le nombre d'arêtes rivières reste inchangé, le nombre d'arêtes non rivières augmente de trois fois le nombre de nœuds sur le bord (cf figure A2C pour la justification de ces formules et Table A2D pour leur présentation).
nœuds |
arêtes |
brins |
facettes |
nœuds sur le bord |
arêtes rivières |
arêtes non rivières |
|
Carte initiale |
n |
a |
2*a |
f |
nb |
nr |
ns |
Carte après création du bord |
n+nb |
a+3*nb |
2*a+6*nb |
f+2*nb |
nb |
nr |
ns+3*nb |
Table A2D : Evolution de la taille d'une carte lors de la création d'un niveau de facettes (verticales) bords.
Par composition de ces opérations dans l'ordre chronologique où elles interviennent, toutes ces quantités peuvent être connues en fonction de la taille de l'arbre initial avant la création effective de la carte.
Exemple
Soit un arbre topologique de 18 nœuds internes, une carte topologique avec lignes de crêtes, une triangularisation globale, puis une triangularisation sur les rivières et enfin création d'un bord de facettes doit être créée. Quelles sont les tailles des tableaux de nœuds et de brins à réserver?
La table suivante établit de proche en proche l'évolution de ces tailles en fonction de l'ordre chronologique des opérations de génération :
nœuds |
arêtes |
brins |
facettes |
nœuds sur le bord |
arêtes rivières |
arêtes non rivières |
|
Carte initiale avec lignes de crête |
5*n+2 |
13*n-1 |
26*n-2 |
8*n-2 |
2*n+4 |
2*n+1 |
11*n-2 |
Carte après retriangularisation globale |
18*n+1 |
50*n-8 |
100*n-16 |
32*n-8 |
4*n+8 |
4*n+2 |
46*n-10 |
Carte après triangularisation sur les rivières |
22*n+3 |
62*n-2 |
124*n-4 |
40*n-4 |
4*n+8 |
8*n+4 |
54*n-6 |
Carte après création des bords |
26*n+11 |
74*n+22 |
148*n+44 |
48*n+12 |
4*n+8 |
8*n+4 |
66*n+18 |
Carte finale pour un arbre initial de 18 nœuds internes |
479 |
1354 |
2708 |
876 |
80 |
148 |
1206 |