RETOUR

Chapitre 1

Etat de l'art en synthèse d'images
de paysages naturels

Dans le cadre de la synthèse d'image, actuellement en plein développement, la modélisation de scènes naturelles et en particulier de paysages représente un challenge particulier en raison de la complexité importante des scènes à synthétiser. Un arbre simple étant composé de plusieurs milliers de branches et de plusieurs dizaines de milliers de feuilles, il sera difficile de gérer en temps réel une animation comportant plus de quelques arbres sur les stations de travail graphiques actuelles (qui peuvent gérer quelques millions de facettes par seconde). Cet aspect du problème en sus de l'intérêt du sujet par lui même, explique probablement les développements constants de la recherche dans ce domaine. Les méthodes développées sont variées et de nombreuses classifications ont été proposées comme par exemple dans Fournier [Fo87]. L'objet de cette introduction est de présenter une telle classification dans les deux domaines qui font l'objet de cette thèse: la modélisation des végétaux et la modélisation de terrain.

Photographie 1A : Exemple de paysage

1.2 Synthèse d'images de végétaux

La littérature comporte un nombre important de travaux ayant pour objet la modélisation et la synthèse d'images d'arbres botaniques par des méthodes informatiques. Ils se caractérisent par la très grande diversité des approches proposées qui peuvent être classifiées en les catégories suivantes :

1.2.1 Les pionniers

1.2.1.1 L'un des tout premiers à s'intéresser à la forme des arbres d'un point de vue informatique graphique fut le Japonais Honda [Hon71] qui dès le début des années 70 s'intéressa aux diverses formes adoptées par un arbre en fonction d'un certain nombre de paramètres à caractère géométrique. Pour rendre la comparaison possible entre les diverses formes, la structure topologique sous-jacente à tous les arbres dessinés est un arbre binaire parfait. Le modèle géométrique définit:

- des rapports de diminution des longueurs des branches : chaque branche fille droite (respectivement gauche) est un segment de droite dont la longueur est raccourcie par rapport à la longueur de sa branche mère d'un rapport R1 (respectivement R2),

- des angles d'embranchement aux différents nœuds : une branche mère non verticale (direction de la gravité) se ramifie en deux branches filles dans le plan qui la contient et qui est perpendiculaire au plan qu'elle forme avec la verticale (Figure 1A). Les angles de déviation q1 et q2 entre les branches filles droite et gauche et leur mère sont fixés. Dans le cas d'une branche mère verticale, le branchement a lieu dans le plan xOz avec les angles q1 et q2 avec la verticale, si les deux angles de déviation (q1 et q2) sont non nuls. Si l'un des deux est nul un traitement particulier a lieu car l'une des branches filles reste verticale, un angle de déviation a en projection dans le plan xOy est alors introduit de proche en proche pour répartir les branches dans l'espace (Figure 1A').

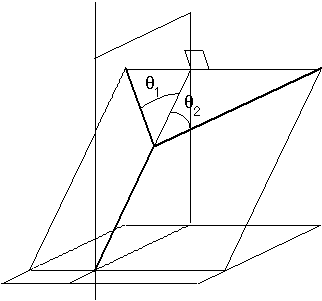
Figure 1A : Géométrie selon Honda (cas général)

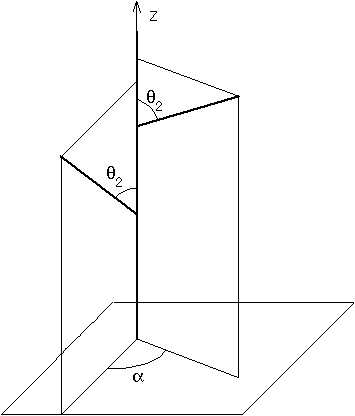
Figure 1A' : Géométrie selon Honda (cas particulier)

Les structures ainsi obtenues sont représentées en fil de fer par Honda de manière à pouvoir analyser facilement leurs formes.

1.2.1.2 Les travaux de Honda furent repris et poursuivis par Aono et Kunii [AK84] qui dans le cadre d'un logiciel appelé A-system, formalisèrent la démarche de Honda à partir de L-systèmes (voir définition des L-systèmes ci-après) très particuliers permettant de générer des arbres binaires ou ternaires parfaits. Pour Aono et Kunii les L-systèmes même s'ils peuvent être améliorés, ne sont pas assez puissants pour modéliser des arbres botaniques car les formes de ces arbres sont trop complexes.

Au niveau géométrique, ils introduisent des variations dans le modèle de Honda pour pouvoir simuler :

- le vent par une déviation uniforme de tous les nœuds ou un tropisme par simulation d'attracteurs ou d'inhibiteurs d'action proportionnelle à leur distance au nœud traité,

- des arbres ternaires,

- une relation entre le niveau des nœuds dans l'arbre et les angles de branchement en ces nœuds.

Enfin ils améliorèrent le rendu des images en attribuant une épaisseur aux branches fonction de leur niveau dans l'arbre et en munissant leurs arbres d'ombres et de feuilles modélisées semble-t-il à partir de nuages de points.

1.2.1.3 Un autre pionnier, Kawaguchi [Ka82], modélise récursivement des formes géométriques du type coraux, cornes, ..., à partir de primitives géométriques simples et de règles de collage de ces primitives. L'élément de base de la construction est un prisme constitué de deux bases (supérieure et inférieure) ayant des formes homothétiques à une forme donnée (souvent une ellipse) (Figure 1B).

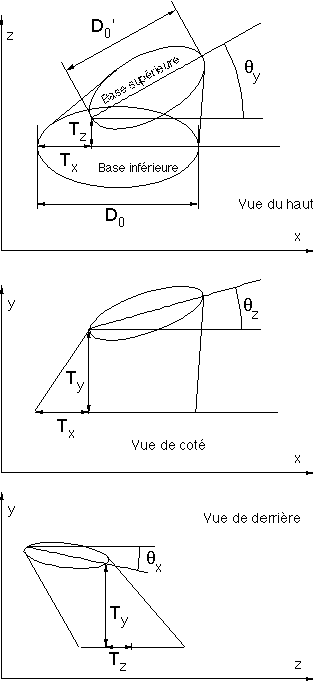
Figure 1B : Géométrie selon Kawaguchi

La position et la taille relative de la base supérieure par rapport à la base inférieure est donnée par (Figure 1B) :

- un rapport appelé taux de croissance,

- un vecteur d'inclinaison (qx,qy,qz) donnant en projection dans les plans orthogonaux aux axes, les trois angles entre les deux plans des bases inférieure et supérieure,

- un vecteur (Tx,Ty,Tz) de translation définissant le déplacement de la base supérieure par rapport à la base inférieure.

L'accumulation récursive de ces prismes permet d'obtenir des cornes telles que celles présentées dans [Ka82].

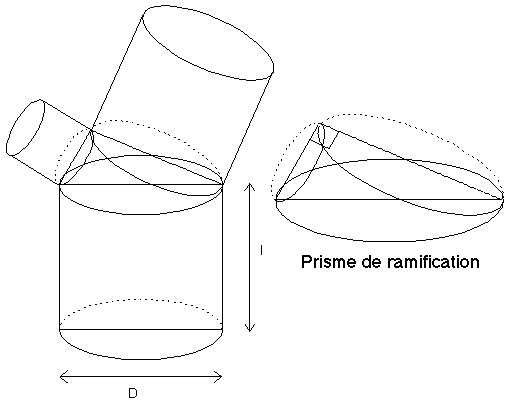
Figure 1B' : Branchement selon Kawaguchi

Pour générer des structures arborescentes, une notion de ramification est introduite, constituée par un prisme ayant une base ellipsoïdale inférieure et deux bases ellipsoïdales supérieures dont les grands-axes sont orthogonaux (figure 1B'). Des cylindres à section ellipsoïdale sont alors liés selon la figure 1B' aux bases de ce prisme. Pour que le modèle soit entièrement défini le rapport hauteur sur base de tous les cylindres intermédiaires est le même. La génération récursive de l'arborescence est stoppée lorsqu'une condition géométrique est vérifiée (par exemple l'épaisseur des cylindres devient inférieure à une valeur limite).

Cette modélisation géométrique est en fait la base d'une série de travaux :

1.2.2 Modélisations issues de la géométrie classique

1.2.2.1 Le modèle de Bloomenthal [Bl85], part d'un arbre topologique préalablement défini appelé squelette. Une caractéristique de ce modèle est de définir pour toute branche mère une branche fille dominante (habituellement celle de plus grande épaisseur). Ce squelette est construit en interpolant chaque suite de n arêtes (n+1 nœuds d'embranchement) commençant par une branche fille non dominante ou par la racine et se poursuivant par la succession des branches filles dominantes à chaque nœud, par une B-spline C2 cubique, c'est à dire n courbes splines consécutives, de façon à obtenir le prolongement par continuité des dérivées première et seconde aux n-1 nœuds d'embranchement intermédiaires. Une telle suite de branches sera représentée par les coefficients des n polynômes cubiques qui la définissent. Ces coefficients sont déterminés par les positions et les tangentes aux n+1 nœuds. Cette méthode des B-Splines permet de fixer arbitrairement la tangente initiale pour la première branche (non dominante), tangente choisie d'autant plus éloignée de la direction de la branche mère que la branche fille est petite.

Figure 1C : Représentation d'une arête par un cylindre généralisé

Figure 1C' : Modélisation d'un embranchement

La modélisation volumique de l'arbre est réalisée en considérant chaque arête comme un cylindre généralisé dont l'axe est la courbe B-spline précitée et dont la section est un cercle de rayon variable (Figure 1C). La modélisation des embranchements est réalisée par des surfaces du type "selle" obtenues en considérant les trois disques représentant les sections circulaires des branches (la mère et ses deux filles), en les reliant par des courbes splines, et enfin en polygonalisant à partir de ces courbes (Figure 1C').

Les angles de branchement entre arêtes, leurs longueurs et épaisseurs sont choisies aléatoirement dans des champs définis en fonction du développement de l'arbre.

Dans cette approche le rendu est tout particulièrement étudié. Par exemple les veines de l'écorce sont obtenues par une technique de modulation de la normale ("Bump Mapping") guidée par l'image aux rayons X du moulage en plâtre d'un morceau d'écorce réel. On crée ainsi un carreau de texture d'écorce qui est ensuite plaqué sur le tronc. Le problème du recollement des bords de deux carreaux de texture connexes est résolu par "mélange" des deux carreaux sur une bande frontière. Les feuilles, elles, sont obtenues par digitalisation de feuilles d'érable réelles et par plaquage de cette image digitalisée sur des surfaces polyédriques. Le nombre de feuilles dessinées sur une branche est fonction de l'épaisseur de cette branche. Le positionnement d'une feuille dans l'espace est fonction de la direction de la branche qui la porte. La gestion des feuilles et d'une texture permet ainsi l'obtention d'images en gros plan très réalistes.

On voit un bel exemple de branches générées par Greene [Gr84] au moyen du modèle de Bloomenthal à la page de couverture des actes de SIGGRAPH'84. Cette image, extraite du film d'animation "Inside a Quark", montre très bien la qualité de texture obtenue par "Bump Mapping".

1.2.2.2 Les travaux d'Oppenheimer [Op86] rentrent également dans le cadre des méthodes issues de la géométrie classique, faisant le lien entre les travaux de Kawaguchi et les méthodes fractales. La structure topologique sous-jacente est constituée d'arbres binaires ou ternaires résultant d'un processus de génération aléatoire assez élémentaire faisant intervenir le nombre de branchements sur chaque segment de branche principal et permettant d'obtenir des arbres auto-similaires et donc fractals (Figure 1D). Oppenheimer reprend les travaux de Kawaguchi en ce sens qu'à partir de quatre primitives géométriques simples : cylindre, spirale, hélice et tortillon, de règles de réduction et de collage faisant intervenir les paramètres suivants :

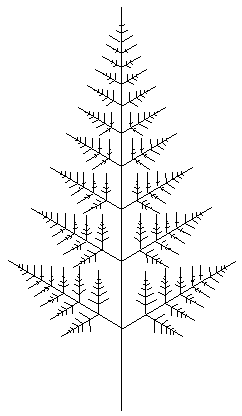
Figure 1D : Topologie selon Oppenheimer

- l'angle entre un segment principal et les arêtes qui s'y connectent,

- le rapport de longueur entre les arêtes principales d'un branchement et les branches qui s'y connectent,

- le rapport de décroissance des arêtes sur un segment,

- la valeur de la rotation hélicoïdale sur les branches,

il construit récursivement les solides 3D en formes de cornes ou spiralées qui sont à l'origine de ses branches.

Pour le rendu, Oppenheimer utilise des vecteurs "anti-aliasés" pour les branches les plus fines, et des prismes polygonaux pour les autres. Les ombrages des facettes sont gérés. Comme chez Bloomenthal, les veines de l'écorce sont réalisées par modulation de la normale, modulation guidée par un mouvement Brownien fractal en forme de vague. Par ailleurs les feuilles qu'il modélise sont obtenues comme limite de l'arborescence fractale des nervures qui les composent.

1.2.3.1 Systèmes de fonctions itérées

Une méthode importante de compression et de restitution d'images est celle fondée sur les systèmes de fonctions itérées (Iterated Function Systems, IFS) développée par Demko, Hodges et Naylor [DH85] ou Barnsley, Jacquin, Malassenet, Reuter et Sloan [BJ88]. Cette technique totalement étrangère à toute analyse de la structure d'un paysage est purement mathématique et est fondée sur des théorèmes ergodiques.

IFS en noir et blanc : A tout ensemble fini de fonctions affines strictement contractantes {wn, 1=n=N} du plan, appelé système de fonctions itérées (IFS pour Iterated Function System), on associe la transformation W qui à B compact du plan associe : W(B)=.

L'attracteur de l'IFS est alors l'unique point fixe A de W sur l'espace complet des parties compactes du plan muni de la distance de Hausdorff ( A=W(A)=), ensemble limite des points itérés zn obtenus à partir d'un point z0 arbitraire du plan, en appliquant de façon itérée avec équiprobabilité les applications wi (zn+1 = wi(zn)).

On remarquera la très forte amplification de ces données qui contrôle la forme d'une image A à partir de 6*N réels définissant les N transformations affines de l'IFS.

Le problème inverse de la détermination d'un IFS ayant pour attracteur une image noir et blanc P donnée, est résolu par Demko et al. en introduisant la notion d'auto-pavage, où l'on recouvre au mieux l'objet A avec un nombre minimum N de copies réduites de lui-même appelées sous-objets. Barnsley et al. proposent un algorithme visuel interactif où l'on réalise à la main sur un écran un pavage du modèle A dont on veut calculer un IFS au moyen de N sous-objets de A. Les N wi correspondant à ces N sous-objets sont automatiquement calculés. Le théorème de collage permet alors de déterminer l'erreur obtenue par rapport à l'image originale en fonction de la précision de l'ajustement obtenu dans le "collage" (Figure 1E).

Figure 1E: Théorème du collage

Si l'on munit d'une probabilité pi (autre que 1/N) la transformation wi, 1=i=N, l'IFS est dit probabilisé. Il y a deux conséquences à l'introduction des probabilités dans les IFS. L'accélération de la vitesse de rendu obtenue en choisissant pi proportionnelle à l'aire wi(P) de l'image produite par wi (Ce qui permet de générer par wi un nombre de points proportionnel à l'aire de wi(P) pour dessiner wi(P)). Dans l'exemple de la figure 1E' de recouvrement de l'attracteur carré, la seconde image obtenue ainsi est meilleure (à nombre de points égal) que la première obtenue par équiprobabilité, puisqu'elle fournit l'image finale du carré à 6 pixels près. On a donc obtenu une vitesse de convergence supérieure par ce choix de probabilités.

Figure 1E' : Exemple de recouvrement de l'attracteur carré avec 100 000 points calculés

La seconde conséquence est l'introduction de la couleur que l'on constate sous forme de tramage dans l'exemple d'un carré recouvert par quatre copies identiques de lui-même (colonne a = (0.5,0.5,0.5,0.5) dans l'exemple précédent). Si l'on génère 10 000 points avec différents choix de probabilités, on obtient :

Dans ces deux situations, les points "tombent" avec différentes fréquences suivant les différents endroits donnant dans les images ci-dessus un "effet de trame" ou de couleur. Les régions les plus sombres sont celles dans lesquelles un plus grand nombre de points sont tombés. Le nombre de points tombant dans une région peut être considéré comme une densité sur cette région. On associe ainsi à un IFS probabilisé, une unique densité portée par l'attracteur A de cet IFS (densité qui est l'unique mesure invariante d'un opérateur contractant défini sur un certain espace métrique complet de mesures boréliennes). Cette mesure assigne à tout pixel de A un nombre positif qui est interprété comme sa couleur: cette mesure est donc une unique façon de colorier A.

Le problème inverse de détermination des probabilités de l'IFS probabilisé permettant de reconstruire une image couleur donnée est complexe et n'est pas traité ici.

Figure 1E'' : Feuille extraite de [Hu91] (2 IFS pour le limbe et le pétiole, N = 10 )

Une nouvelle transformation CB peut être ajoutée à un IFS et permet d'obliger l'attracteur de l'IFS à contenir un ensemble donné appelé ensemble de condensation B. Une hiérarchie d'IFS est alors définie comme étant une suite ordonnée d'IFS avec ensemble de condensation, chaque ensemble de condensation étant l'attracteur de l'IFS précédent. L'intérêt des hiérarchies d'IFS avec ensembles de condensation est qu'elles permettent de réduire le nombre de fonctions affines nécessaires au rendu d'un paysage complexe, en rendant compte des hiérarchies topologiques entre éléments végétaux (branche -> arbre -> forêt).

Un autre aspect intéressant de la génération d'images par IFS est que le caractère fractal des images obtenues permet d'obtenir des agrandissements à toute échelle de l'objet modélisé tout en gardant le même code en mémoire et la même précision de rendu. Le calcul itératif de l'image se poursuit jusqu'à l'obtention d'une image suffisamment consistante. Les couleurs sont obtenues en réglant les probabilités Pi et par un choix convenable de la fonction liant les caractéristiques chromatiques avec la fréquence d'apparition en un pixel des points de l'attracteur dans le procédé itératif.

Les images obtenues représentent souvent des objets à forte caractéristique auto-similaire (feuilles d'érable, fougères). Dans les exemples donnés (images de la côte de Monterey, de la forêt noire, d'un champ de tournesols,... (cf [BJ88]), le nombre d'applications affines des IFS est de 160 à 180. Ces nombres sont réduits à environ 100 par l'utilisation de la notion de hiérarchie d'IFS avec ensemble de condensation, correspondant à la hiérarchie des éléments végétaux.

1.2.3.2 Systèmes de particules

Un second modèle entrant dans la catégorie des méthodes fractales, permettant d'obtenir des résultats de type impressionniste, a été développé par Reeves [Re83] et Reeves et Blau [RB85] : il s'agit des systèmes de particules. Par cette approche, l'objet modélisé est considéré comme un flot de particules évoluant dans R3. Une image représentera les trajectoires de ces particules. Si l'on modélise le feu, les particules issues d'un foyer commun seront toutes indépendantes et seront essentiellement des points lumineux caractérisés par leur forme, couleur, trajectoire (position et vitesse à tout instant), date de naissance et de mort .

Trois raisons expliquent l'intérêt de ce type de modélisation :

- Une particule ponctuelle est la plus simple des primitives graphiques imaginable. Un très grand nombre pourra en être dessiné dans le même laps de temps, des objets avec plus de détails pourront donc être obtenus.

- Les systèmes de particules sont procéduraux et stochastiques : on peut minimiser le temps passé à la modélisation car un faible nombre de paramètres initiaux permettent d'obtenir des images très fouillées, on dit qu'il y a un grand taux d'amplification des données.

- Ils permettent de modéliser des scènes dynamiques (feu, vent dans de l'herbe).

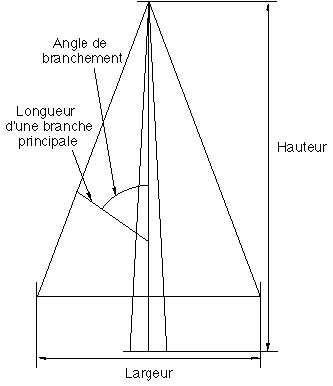
Figure 1F : Géométrie selon Reeves et Blau

Les systèmes de particules qui permettent de générer des images d'arbres botaniques ou d'herbe sont structurés et donc composés de particules non indépendantes. Chaque arbre est représenté comme un ensemble d'arêtes pour les branches et de petits cercles pour les feuilles. Les feuillus auront la forme d'ellipsoïdes tandis que les arbres à feuillage persistant ressembleront à des cônes (Figure 1F). De nombreuses relations existent entre les particules modélisant un arbre car elles doivent constituer un objet 3D cohérent. Chaque type d'arbre possède son propre modèle dans une base de données. Ce modèle est défini par un ensemble de contraintes sur les paramètres le caractérisant, contraintes qui définissent les intervalles autour d'une valeur moyenne dans lesquels les paramètres sont choisis avec équiprobabilité et qui lient les paramètres entre eux. Un algorithme récursif génère les branches à partir de paramètres et de relations permettant de définir le type de branchement, la distance entre deux sous-branches consécutives, l'angle de la branche au tronc, sa longueur et son épaisseur. Chaque branche hérite d'une grande partie des paramètres de ses parentes (éventuellement remis à l'échelle). La récursion est arrêtée quand l'épaisseur de la branche atteint une valeur minimale limite ou quand un certain niveau de profondeur est atteint.

Les problèmes de rendu qui se posent à Reeves et Blau sont d'un tout autre ordre que pour les autres auteurs. En raison du caractère "impressionniste" du modèle, un très grand nombre de particules devront être générées pour obtenir un objet consistant.

Les algorithmes classiques de représentation en faces cachées utilisés pour la visualisation sont inopérants en raison du trop grand nombre de primitives graphiques à gérer. La méthode proposée est celle du peintre après un tri de paquets de particules ainsi réalisé (1) trier en z les arbres constituant le paysage, (2) appliquer l'algorithme suivant sur chacun des arbres indépendamment de tous les autres. Chaque arbre est décomposé en tranches en fonction de la distance en z, lorsqu'une particule est générée, elle est insérée dans la tranche (paquet) correspondant à sa distance en z moyenne. 2000 tranches sont habituellement utilisées pour un arbre.

Par ailleurs, pour rendre les ombres portées il n'est pas non plus possible d'utiliser un algorithme classique. Reeves et Blau proposent une méthode statistique. La lumière illuminant chaque particule est formée de trois composantes (Figure 1F'):

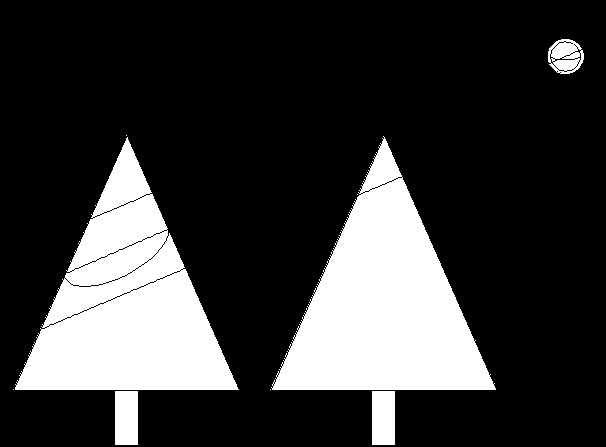
Figure 1F'' : Ombres portées

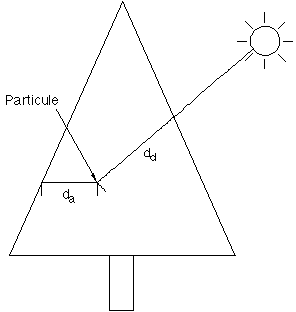
Figure 1F' : Distances dans un arbre

- une composante D de lumière diffuse exponentiellement décroissante de la distance dd dans l'arbre à la source lumineuse (D = e-add),

- une composante A de lumière ambiante exponentiellement croissante de la distance horizontale da de la particule au bord extérieur de l'arbre et minorée par une valeur minimale d'éclairage ambiant Amin (A = max(e-bda,Amin)),

- une composante S de lumière spéculaire pour les particules de distance dd faible et dont la branche associée est perpendiculaire à la direction d'incidence des rayons lumineux.

Enfin l'ombre portée d'un arbre sur un autre arbre est gérée en considérant que les composantes diffuse et spéculaire n'existent qu'au dessus du plan figuré sur la figure 1F''. En dessous de ce plan, elles sont de moins en moins prises en compte jusqu'à être totalement ignorées. Les résultats obtenus sont tout à fait réalistes avec un luxe de détails ponctuels propres aux systèmes de particules. La réalisation de clairières est un exemple frappant de la qualité des résultats obtenus par gestion statistique de l'éclairage et des ombres portées. Les temps de calcul et d'affichage annoncés sont en contrepartie de plusieurs heures en raison de l'importance des calculs.

Cette technique se caractérise enfin par une aptitude particulière à modéliser des séquences animées, en particulier les systèmes de particules ont été utilisés pour la réalisation d'une spectaculaire séquence d'effets spéciaux du film de cinéma "Star Trek II, la colère de Kahn" où l'on voit un mur de feu recouvrir une planète. L'aspect dynamique de la modélisation par des particules mobiles rend intrinsèque le mouvement dans des scènes changeantes au cours du temps.

1.2.4 Modèles combinatoires

1.2.4.1 De tels modèles sont présentés dans Eyrolles, Françon et Viennot [EF86], Eyrolles [Ey86] et Viennot, Eyrolles, Janey et Arquès [VE89a] [VE89b] [VJ90], qui seront décrit dans le chapitre 3 (non détaillé ici). Il permet la génération d'arborescences ressemblant à des arbres botaniques à partir d'un processus utilisant des paramètres à caractère purement combinatoire.

1.2.4.2 La modélisation des feuilles végétales a été abordée par Lienhardt [Li87] et Lienhardt et Françon [LF87] par une approche combinatoire. Ils se basent sur l'utilisation de connaissances botaniques appliquées à un modèle où la topologie prime sur la géométrie pour simuler une évolution des feuilles au cours du temps.

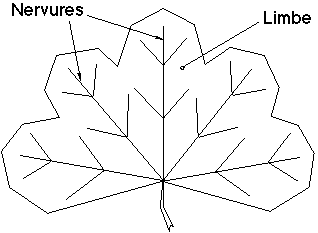
Figure 1G : Une feuille

Le modèle est basé sur la constatation que le limbe d'une feuille forme une surface s'appuyant sur des nervures constituant elles-même un arbre enraciné (Figure 1G). Le développement de l'architecture des nervures au cours du temps est assez proche de celui des axes d'un arbre. Les notions propres aux axes des arbres (ramification, mortalité, rythme, ... voir plus loin) peuvent être étendues aux nervures d'une feuille.

Le modèle topologique d'une feuille est un graphe modulaire comprenant :

- deux types d'arêtes : des arêtes de croissance et des arêtes de résistance,

- deux types de sommets : des sommets de croissance (incidents à au moins une arête de croissance) et des sommets de résistance (incidents à aucune arête de croissance),

- deux types de faces : des faces d'activité (incidentes à au moins une arête de croissance) et des faces frontières (incidentes à aucune arête de croissance).

Les sommets et arêtes de croissance symbolisent la nervation de la feuille. Le sous-graphe modulaire restreint à ces seuls sommets et arêtes est un arbre appelé arbre de croissance (Figure 1G'). A ce titre les arêtes de croissance sont donc orientées.

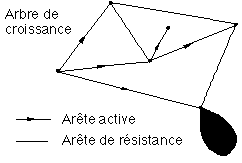
Figure 1G' : Arbre de croissance

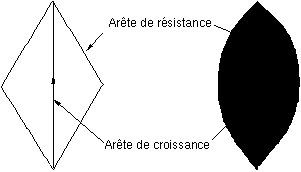
Figure 1G'' : Deux types de modules élémentaires

Un graphe modulaire est planaire. Il est construit à partir des deux modules élémentaires (Figure 1G'') existants définis par deux faces triangulaires ayant une arête de croissance en commun, les autres arêtes et sommets étant de résistance.

Figure 1H : ramification

Figure 1H' : Création de face frontière par fusion

Une feuille est obtenue par simulation discrète de son développement au moyen d'opérations topologiques appliquées au seuls éléments de croissance. Deux des principales opérations sont (Figures 1H et 1H'):

- la ramification, où l'on voit la création à partir d'un sommet de croissance, d'une nouvelle arête de croissance et du module élémentaire correspondant (plusieurs résultats possibles),

- la fusion ou la disjonction qui entraînent la création ou la suppression de faces frontières, l'allongement ou le raccourcissement de faces frontières.

L'enchaînement des opérations topologiques de génération d'une feuille est réalisée au moyen de fonctions de développement qui permettent de définir, séquencer et caractériser les opérations applicables à une feuille. Ces fonctions, appliquées à tout élément de croissance au cours de la génération, font intervenir l'horloge t, la date de création de l'élément de croissance sur lequel porte la fonction, l'intensité de l'élément de croissance (ordre entier associé à tout arête de croissance), les distances entre cet élément et ses éléments ascendants (paramètres voisins des notions d'âge, d'ordre, de dimension du modèle botanique de de Reffye).

Pour le calcul de la géométrie et le rendu, un certain nombre de fonctions de complément définissent les aspects non topologiques de la feuille tels que les longueur, diamètre et angles 3D entre les arêtes de croissance filles d'un sommet, ou les caractéristiques chromatiques.

Ce modèle permet de générer des feuilles d'une grande diversité de formes. Un aspect intéressant est que, par non remplissage des faces frontières, on peut obtenir des feuilles "trouées". Le temps de calcul d'une feuille varie de quelques secondes à plusieurs minutes, pour obtenir des graphes de quelques centaines à plusieurs milliers de facettes triangulaires.

1.2.5.1 L-Systèmes

Les méthodes basées sur les L-Systèmes (grammaires de réécriture parallèle) permettent de simuler au niveau topologique la croissance botanique des arbres, voir par exemple Smith [Sm84], Prusinkiewicz [Pr86], Prusinkiewicz, Lindenmayer et Hanan [PL88], Prusinkiewicz et Hanan [PH89] et Prusinkiewicz et Lindenmayer [PL90].

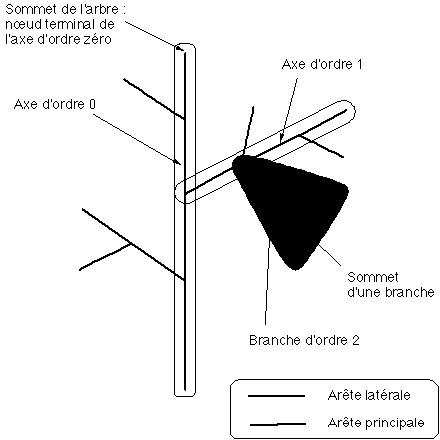
Figure 1I : Arbre axial selon Prusinkiewicz

Cette modélisation topologique est fondée sur la notion d'arbre axial (Figure 1I):

- A chaque nœud on distingue au plus une arête fille appelée arête principale, les autres arêtes issues de ce nœud étant appelées arêtes latérales.

- Un axe est une sous-suite maximale d'arêtes commençant par l'arête issue de la racine ou bien par une arête latérale, et continuant par une sous-suite maximale d'arêtes principales .

- Le sommet terminal de l'axe issu de la racine est appelé sommet de l'arbre.

- Une branche est l'ensemble constitué d'un axe et de tous ses axes descendants dans l'arbre. Une branche est elle-même un arbre axial .

Des ordres à valeurs numériques sont attribués aux axes et par la même aux arêtes :

Figure 1I' : Codage d'un arbre

Figure 1J : Règle de production et application de cette règle à l'arête étiquetée S d'un arbre axial

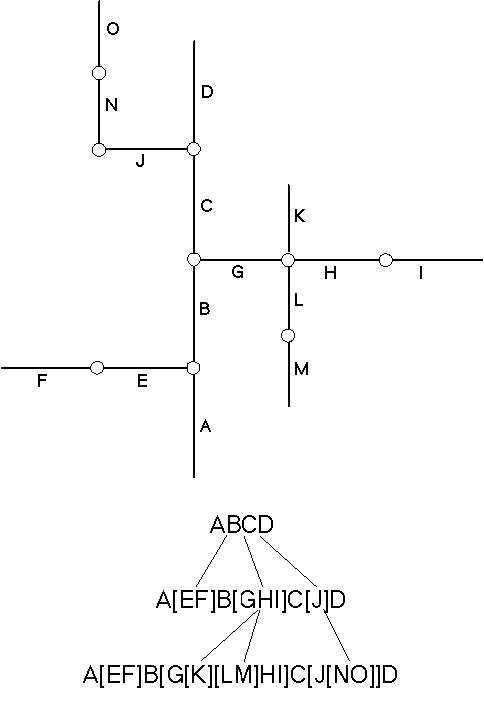
- L'axe dont l'arête racine est la racine de l'arbre a l'ordre 0.

- Les axes d'ordre i commencent par une première arête latérale issue d'un axe d'ordre i-1.

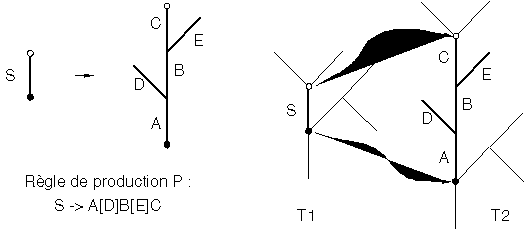
Une méthode simple de représentation d'un arbre axial dont les arêtes sont étiquetées par les lettres d'un alphabet V consiste à le coder au moyen d'un mot sur l'alphabet V U {[,]}, où les crochets [ et ] codent les branches, selon l'exemple de la figure 1I’ qui décrit la construction du codage d’un arbre.

La croissance topologique dans ce modèle est alors guidée par la réécriture parallèle de toutes les arêtes étiquetées de l'arbre axial courant selon le système de réécriture appelé arbre-0L-System défini comme le triplet (V,w,P) où :

- V est un alphabet,

- w est un mot de V appelé axiome représentant un arbre axial,

- P est un ensemble de règles de production associant à chaque lettre de l'alphabet V un arbre axial, selon l'exemple de la figure 1J.

Figure 1J' : Evolution d'un arbre selon un arbre-0L-système

La génération de l'arbre s'effectue par un processus itératif débutant par l'axiome w, et remplaçant à chaque itération simultanément chaque arête étiquetée de l'arbre par l'arbre axial correspondant à la règle de production trouvée dans P associée à son étiquette, les deux sommets de l'arête étant remplacés par les deux sommets extrémités (racine et sommet de l'arbre) de l'axe d'ordre 0 de l'arbre axial que l'on substitue à l'arête (Figure 1J').

Figure 1J'' : Contexte BC < S > G[H]M et exemple d'apparition dans un arbre axial

Une grande influence est donnée à la topologie par paramètrage des règles de réécriture. Dans les exemples précédents, celles présentées sont indépendantes du contexte, constitué par les arêtes situées en amont (contexte à gauche) et en aval (contexte à droite) de l'arête étudiée. Précisément, on appelle contexte gauche CG d'une arête S de l'arbre toute suite d'arêtes ancêtres de S dans l'arbre et aboutissant en S, et on appelle contexte droit CD de S, tout arbre axial issu en aval de l'extrémité finale de S (Figure 1J''). On note alors CG<S>CD ----> T une règle de production s'appliquant à l'arête étiquetée S et remplaçant S par l'arbre axial T dans le contexte considéré. L'utilisation de règles dépendant du contexte permet la simulation de phénomènes tels que la propagation temporelle d'informations de la racine de l'arbre vers les feuilles (propagation acropétale) ou des feuilles vers la racine (propagation basipétale) (Figure 1K) ou l'évolution du type des nœuds (un nœud peut d'abord donner des feuilles puis ensuite des fleurs).

Figure 1K : Signal de propagation acropétale et basipétale

La modélisation géométrique est effectuée au cours d'une seconde passe appelée "interprétation", après la création du mot décrivant la topologie de l'arbre.

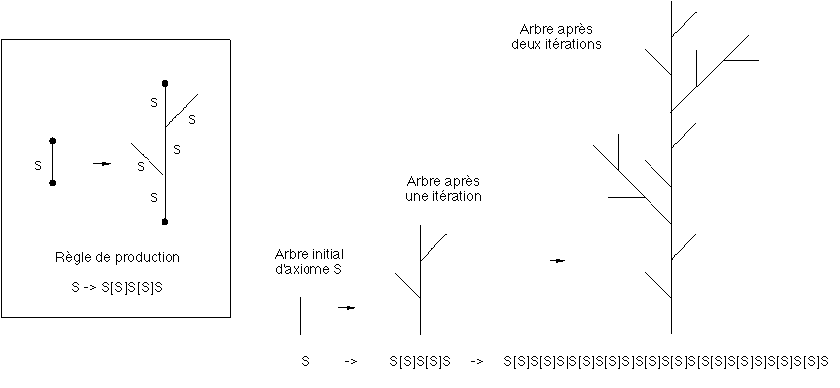
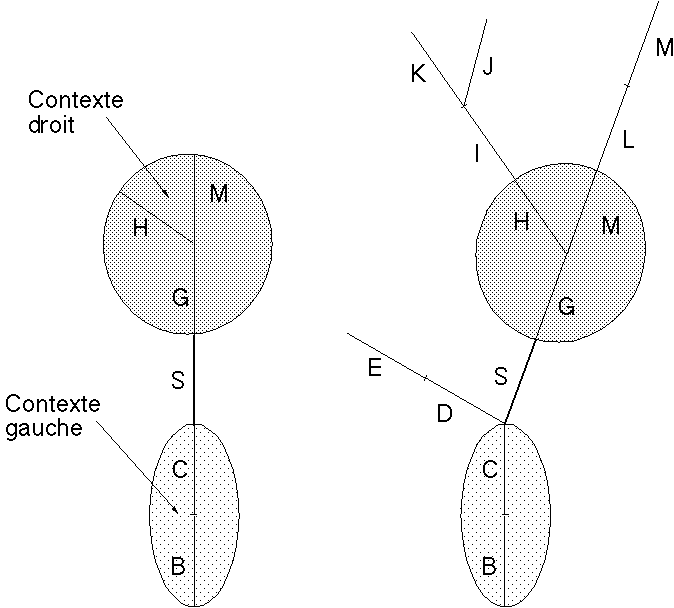
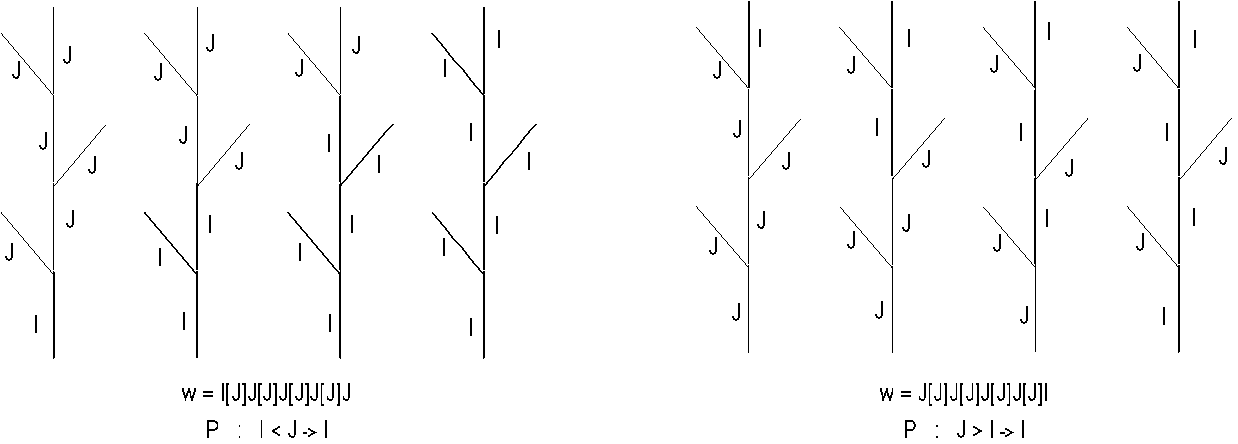
Chez Smith, les branches et les feuilles sont modélisées par des lignes et des disques en 2D et par des cylindres et des sphères en 3D. Smith ne décrit pas précisément les lois géométriques employées, en particulier pour le calcul des angles d'orientation. Il signale seulement la possibilité offerte par le logiciel Gene de définir un ensemble d'angles, en soulignant que l'utilisation de variables aléatoires n'est pas nécessaire pour obtenir de beaux résultats.

Nombre de générations = 4, d = 22.5°, V = {F}, F -> FF-[-F+F+F]+[+F-F-F]

Figure 1L : Arbre généré par arbre-0L-système avec une géométrie 2D

En revanche, Prusinkiewicz et al. abordent le problème du calcul d'une géométrie appliquée à un mot généré par un L-system beaucoup plus finement que Smith. La géométrie est construite au moyen d'une tortue de type LOGO qui interprète le mot créé par le L-Système sous forme d'instructions à caractère géométrique. En 2D, certaines lettres du langage (+, -) indiquent des déviations positives ou négatives d'un angle d par rapport à l'axe de la tortue (Figure 1L). Les étiquettes associées aux arêtes de l'arbre codent le déplacement de la tortue sur une longueur d. En 3D un repère

Les symboles [ et ] permettent la gestion d'une pile d'états de la tortue pour les retours d'interprétation de branches aux nœuds d'embranchement. D'autres symboles peuvent encore être ajoutés pour contrôler la couleur, le diamètre et la longueur des segments, pour incorporer et remplir des surfaces (feuilles),...

En ce qui concerne le rendu, Prusinkiewicz et al. franchissent un grand pas vers le réalisme. L'utilisation des feuilles modélisées directement par L-système géométrique et d'une modélisation volumique des branches rend les dessins beaucoup plus réalistes. L'utilisation de L-Systèmes stochastiques permet d'introduire de la variété dans les végétaux dessinés.

1.2.5.2 Grammaires d'arbres

Une autre approche, développée par Shao [Sh92], consiste à générer des arbres enracinés par utilisation de systèmes de règles de réécriture parallèles (remplaçant les sommets par des arbres) appelés grammaires d'arbres. Ces travaux se distinguent de ceux de Prusinkiewicz sur le point particulier que la réécriture est effectuée par remplacement par des arbres de sommets et non pas seulement d'arêtes. Des extensions sont proposées par introduction de contexte de suppression d'arbre et de choix stochastique des règles employées.

Les paramètres géométriques mis en œuvre sont classiques. Ils font intervenir des longueurs d'arêtes et des angles de branchement fonction des ordres. L'arbre est modélisé par des segments pour les arêtes et des sphères pour les sommets. Une forme 3D est considérée comme limite d'une arborescence évoluant en 3D justifiant ainsi l'emploi de sphères pour les sommets. Cette idée généralise en 3D celle développée par Oppenheimer, faisant apparaître une feuille comme la limite fractale de l'arborescence de ses nervures. Le rendu est réalisé au moyen d'algorithmes classiques (Z-Buffer, illumination calculée au moyen de la normale) améliorés pour le rendu de surfaces modélisées par des sphères.

Ces travaux sont présentés par décomposition en trois noyaux logiciels de manière à bien faire apparaître la disjonction entre les aspects topologiques, géométriques et infographiques. Le paramètrage des lois permet d'obtenir des objets fractals, mais aussi des objets ressemblant à des arbres botaniques (brocoli, choux fleur par exemple).

1.2.6 Modèles botaniques

Figure 1M : Définitions

Le modèle botanique de de Reffye, Edelin, Françon, Jaeger, Puech [RE88], Jaeger [Ja87] simule la croissance de végétaux au moyen de règles purement botaniques extraites d'analyses empiriques réalisées sur le terrain. Ils permettent ainsi l'obtention théorique de toute espèce existant dans la nature.

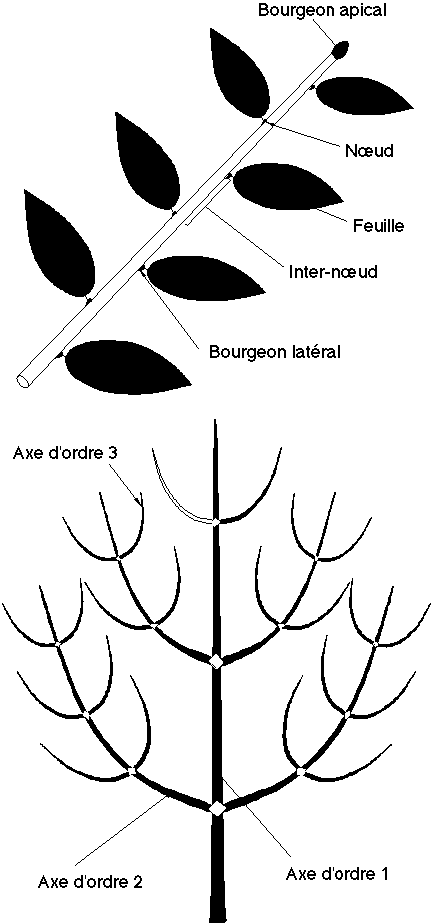
L'élément fondamental de l'architecture d'un arbre est l'axe. La croissance de tout axe résulte de l'activité du bourgeon situé à son extrémité, bourgeon appelé bourgeon apical. Un axe est constitué d'un ensemble d'internœuds créés les uns après les autres. Entre deux internœuds existe un nœud qui donne naissance à des feuilles et à des bourgeons latéraux. La naissance d'un axe à partir d'un bourgeon latéral est appelée ramification. A une unité près, on définit sur les arbres botaniques la même notion d'ordre attribué au axes et aux nœuds que sur les arbres générés par arbres-L-systèmes par Prusinkiewicz et al. (voir ci-dessus). L'axe d'ordre 1 est l'axe associé au nœud racine. Un axe d'ordre k prend naissance sur un bourgeon latéral d'un axe d'ordre k-1 (Figure 1M).

La ramification au niveau des bourgeons latéraux s'effectue selon plusieurs modes :

- ramification continue : tout bourgeon latéral d'un axe donne naissance à un nouvel axe,

- ramification rythmique : seuls certains bourgeons latéraux répartis régulièrement donnent naissance à un nouvel axe,

- ramification diffuse : seuls certains bourgeons latéraux répartis aléatoirement donnent naissance à un nouvel axe.

Le modes de ramification latérale et de croissance apicale de chaque axe sont fonctions de l'ordre de l'axe considéré suivant les espèces modélisées.

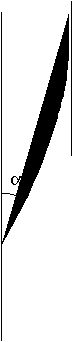
Orthotropie           Plagiotropie

Figure 1M' : Tendances de croissance

Au niveau géométrique les axes adoptent généralement une tendance orthotropique (croissance des axes en direction verticale) ou plagiotropique (croissance des axes en direction horizontale) (Figure 1M').

Un arbre monopodial d'ordre k est un arbre possédant un seul axe d'ordre 1 et un nombre fini d'axes d'ordre compris entre 1 et k. La croissance des axes peut ne pas être uniquement monopodiale, en particulier si un bourgeon apical meurt (mort naturelle ou taille de l'axe), il peut y avoir réitération et création à partir de bourgeons latéraux de nouveaux axes à la place de ce nœud. On dit qu'on a alors une croissance sympodiale.

Croissance sympodiale orthotropique

Ramification continue

Figure 1N: Modèle de Leeuwenberg

Croissance monopodiale orthotropique sur l'axe d'ordre 1 et plagiotropique sur les autres

Ramification rythmique

Figure 1N' : Modèle de Massart

Hallé, Oldeman et Tomlinson [HO78] ont recensé 23 modèles architecturaux pour les arbres des forêts tropicales (exemples aux figures 1N et 1N'). Leur classification est principalement basées sur :

- la présence ou l'absence de croissance sympodiale,

- le type de ramification,

- la croissance continue ou non,

- la tendance plagiotropique ou orthotropique.

De Reffye et al. modélisent l'évolution d'un arbre par un processus de croissance discret basé sur l'activité des bourgeons et faisant intervenir la croissance, la ramification et la mort de ces bourgeons.

La croissance de l'arbre est rythmée par les tops d'une horloge. Chaque axe de l'arbre croit d'une unité de croissance (séquence d'internœuds) entre chaque top d'horloge. La durée entre deux tops d'horloge est supposée constante pour tous les axes de même ordre, ce qui implique que la croissance peut être plus ou moins rapide suivant les axes.

Deux probabilités sont attribuées à chaque bourgeon (Figure 1O) :

- une probabilité de mort (pour un bourgeon latéral cette probabilité est la probabilité de non ramification),

- une probabilité de pause.

Pmort = Ppause = 0

Pmort = 0

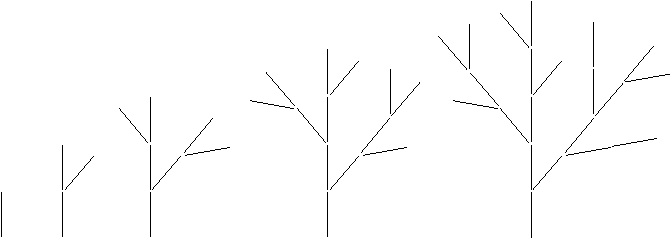
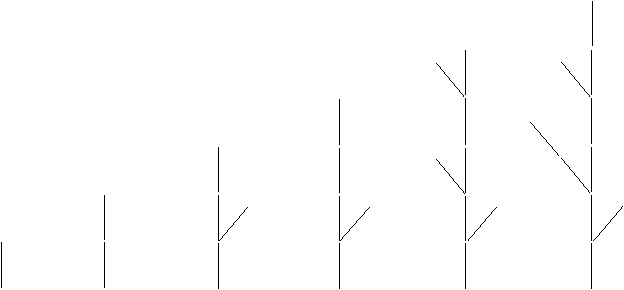
Ppause = 0 sur l'axe 1, sinon Ppause grande

Figure 1O : Croissances topologiques

Pour une espèce particulière, des probabilités ne sont fonction que de l'âge (date de naissance suivant l'horloge), la dimension (durée entre la naissance d'un bourgeon et la naissance de l'axe qui le porte) et l'ordre du bourgeon considéré.

La génération d'un arbre demande la connaissance d'un certain nombre d'autres paramètres : l'âge de l'arbre que l'on veut générer, les vitesses de croissance des axes (en fonction de l'ordre), le nombre de bourgeons à chaque nœud (en fonction de l'ordre), la probabilité de réitération sur un bourgeon (fonction des mêmes paramètres que les probabilités précédentes).

L'algorithme suivant décrit de manière très simplifiée la génération de l'arbre :

Pour chaque bourgeon b à chaque top horloge faire
	Si b ne meurt pas alors
		Si b n'entre pas en pause alors
			création d'un internœud
			création d'un bourgeon apical
			Si b se ramifie alors
				création de bourgeons latéraux
			Finsi
		Finsi
	Finsi
Finpour          

Dans la pratique, pour des raisons d'implantation mémoire, l'arbre est généré à partir de l'utilisation d'une pile de bourgeons, sans conservation globale de la structure. La génération d'arbres de plusieurs centaines de milliers de nœuds est ainsi possible, mais la simulation de la croissance est rendue plus difficile car un arbre entier doit être généré pour chaque étape de l'évolution.

Au niveau géométrique, la portion de branche correspondant à un internœud est modélisée par un cylindre ou un cône. Les longueurs et diamètres des internœuds sont des fonctions de l'ordre, de l'âge et de la dimension. Les angles d'insertion (a sur la figure 1M') et de phyllotaxie (angle d'une feuille ou d'une branche dans le plan perpendiculaire à l'axe de la branche la portant) sur les axes sont des variables aléatoires fonctions de ces mêmes paramètres. Il peut aussi être tenu compte de la pesanteur et de la flexibilité des branches (calcul de résistance des matériaux).

Le résultat de l'exécution du générateur de plantes est un fichier de composantes botaniques qui peuvent être des internœuds, des feuilles, des fleurs, des fruits,... ainsi que les informations géométriques nécessaires à leur placement dans l'espace. A chacun de ces éléments correspond une primitive graphique dans une bibliothèque de formes, par exemple un cylindre hexagonal ou un cône tronqué pour un internœud ou bien des polygones pour les feuilles. Cette librairie peut être paramétrée en fonction de l'âge de l'arbre. La qualité de la visualisation (qui est très bonne) ne semble pas tributaire de l'utilisation de formes complexes (prismes à 6 faces latérales, feuilles composées de 4 facettes), ni de techniques infographiques complexes (facettes monochromes, Z-buffer pour l'affichage, pas d'anti-aliasing, ni de plaquage de texture).

Du point de vue de l'utilisateur, le nombre de paramètres à fournir pour générer un arbre croît rapidement avec la complexité de l'arbre à modéliser (quelques dizaines pour un petit arbre, plusieurs centaines pour un arbre important). Les temps de calcul et d'affichage suivent le même processus (de quelques minutes à plusieurs dizaines de minutes).

1.2.7.1 Modèle évolutionniste

Le modèle environnemental de Niklas [Ni86] analyse en fonction de paramètres géométriques, la forme des arborescences selon des critères tels que l'adaptation à la captation de la lumière ou à la résistance à la pesanteur, de manière à caractériser l'évolution de la forme des arbres au cours des quelques dizaines de millions d'années ayant suivis leur apparition sur Terre. Son raisonnement se base sur l'affirmation que les arbres sont des solutions structurelles au problème biochimique de la photosynthèse. C'est à dire que les plantes dont la forme leur permet le mieux de capter la lumière auront plus de chances de survie que les autres. En conséquence l'évolution d'une espèce aura tendance à renforcer ce caractère par sélection naturelle. Une hypothèse à caractère structurelle doit aussi être vérifiée, pour supporter des contraintes mécaniques et donc ne pas s'écrouler sur elle-même, une plante doit pousser verticalement.

La modélisation de Niklas repose sur l'utilisation d'arbres binaires engendrés par un processus itératif où à chaque étape une certaine proportion de nœuds terminaux se ramifient.

Fig 1P : Géométrie selon Niklas

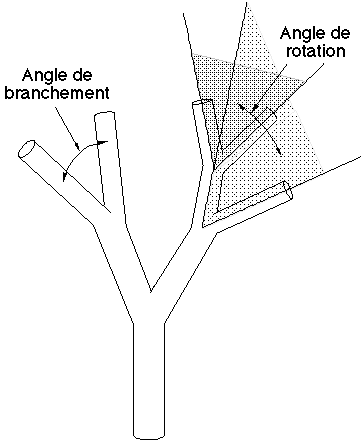
La géométrie de l'arbre est calculée à partir de deux angles, l'angle de branchement constant qui détermine l'angle entre les deux arêtes filles d'un nœud, et l'angle de rotation qui détermine la valeur de la rotation entre le plan formé par les arêtes filles d'un nœud n et le plan formé par l'arête mère de n et son arête sœur, angle calculé aléatoirement dans un intervalle donné (Figure 1P). La manière avec laquelle l'angle de branchement est réparti entre les deux arêtes filles n'est pas indiquée, les images proposées laissent supposer qu'il peut être alloué soit équitablement, soit entièrement à l'une des deux branches filles. La longueur des arêtes semble être constante dans l'ensemble de l'arborescence. Ces arbres sont simplement dessinés en fil de fer, le but de Niklas n'étant pas l'obtention d'images photoréalistes.

1.2.7.2 Modélisation dans l'espace des voxels

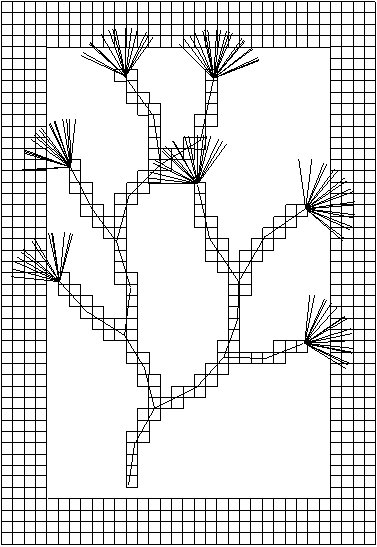
Le modèle de Greene [Gr89] réalise la croissance d'une l'arborescence botanique dans un espace subdivisé en un ensemble de cubes identiques appelés voxel (Voxel Space) en fonction de contraintes environnementales telles que l'ensoleillement ou la présence d'obstacles physiques.

Greene utilise des arbres binaires engendrés par un processus stochastique dont l'un des moyens de contrôle est un retour de la géométrie sur la topologie avec pour conséquence une limitation de leur évolution. Cet arbre ne semble pas codé explicitement au cours de la modélisation. Le modèle géométrique conçu par Greene est grandement influencé par les particularités de l'espace de travail utilisé: un espace Voxel est l'équivalent en trois dimensions d'une image bitmap en deux dimensions. Un objet (ligne, polygone, polyèdre) sera représenté comme un ensemble de voxels occupés. L'environnement proche d'un objet étant alors formé des couches successives de voxels voisins de ceux occupés par l'objet.

L'intérêt de l'utilisation d'un espace discret dans le cadre de la modélisation 3D, est que certaines manipulations sont grandement facilitées par rapport à des espaces plus classiques (euclidiens). On citera le test d'intersection (par test d'occupation de tous les voxels), le test de proximité (à l'aide des couches successives de voxels voisins) ou la mesure de la distance entre deux objets complexes. Les opérations effectuées dans un espace voxel sont forcément approximées en raison du caractère discret inhérent à l'espace, mais les avantages en vitesse et en facilité de travail peuvent être déterminants. Ceci est le cas pour la réalisation d'automates de croissance sensitifs à l'environnement (les obstacles doivent être évités, la proximité de certains objets peut inhiber ou favoriser la croissance, l'évolution est modulée par la lumière).

Figure 1Q : Retour de la géométrie sur la topologie pour la croissance

L'algorithme de croissance utilisé par Greene consiste dans un premier temps, à initialiser l'espace voxel, à définir ensuite des points sources, et enfin, à partir de ces points à générer des éléments géométriques (des branches) selon un ensemble de contraintes. Ces contraintes sont de deux types, soit géométriques pures comme la longueur et l'épaisseur des arêtes ou les valeurs des angles de branchement (utilisation de variables aléatoires), soit environnementales qui sont de deux types :

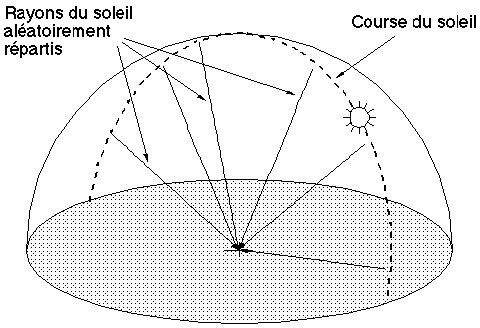
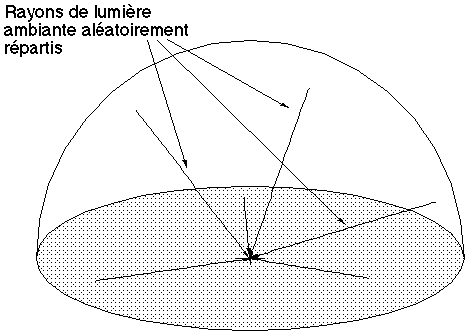
- non intersection et non proximité avec les objets déjà existants,

- illumination suffisante pour qu'un nœud puisse évoluer.

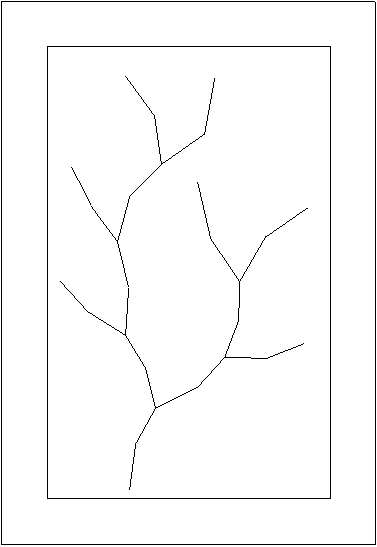
Des tentatives de génération sont effectuées jusqu'à trouver une position acceptable dans la limite d'un nombre d'essais maximum donné (voir la figure 1Q gauche où les essais infructueux (éventails) marquent les arrêts dans les ramifications).

Figure 1Q': Calcul de l'illumination du soleil et de l'illumination ambiante

Le calcul de l'illumination tire partie des spécificités de l'espace voxel. L'illumination d'un voxel est la somme de deux valeurs, une illumination venant du ciel entier et une illumination venant du soleil tout au long de sa course quotidienne. Il est simple de vérifier si un rayon (un segment de droite) coupe l'un des objets présents dans l'espace voxel. L'illumination du ciel sera la proportion de rayons non interceptés par un voxel déjà occupé venant de la demi-sphère céleste et allant vers le voxel testé (test sur 100 rayons répartis avec homogénéité sur la sphère céleste), l'illumination du soleil sera la proportion de rayons non interceptés venant du soleil (test sur 100 rayons répartis sur l'arc semi-circulaire matérialisant la course du soleil dans le ciel) (Figure 1Q').

Les images présentées par Greene ont été obtenues par des techniques classiques de rendu par facettes. La gestion des couleurs attribuées à ces facettes s'effectue par codage direct au niveau des voxels. La taille de l'espace voxel est comprise entre 150x150x150 et 300x300x300, il y a donc entre 3 et 27 millions de voxels. Logiquement, le temps de construction des arborescences croît proportionnellement avec le nombre de voxels dans l'espace, les temps signalés sont d'environ 30 heures de calcul.

Le dessin d'une image peut représenter la gestion de plusieurs centaines de milliers de facettes, mais les résultats obtenus sont très réalistes. La génération de l'arborescence s'accompagne de la génération de feuilles polygonales. La gestion des bâtiments à la base même de la méthode apporte un grand avantage par rapport à toutes les autres techniques pour la réalisation de paysages composites. Un problème reste toutefois les exigences matérielles liées à la gestion d'un espace Voxel.

Un autre travail utilisant une modélisation dans un espace Voxel est celui de Blaise [Bl91] qui à partir du modèle de croissance de de Reffye et Jaeger ([RE88], [Ja87]) permet la simulation de contraintes d’ensoleillement ou de contraintes géométriques (lors de l’évolution d’une branche, la présence de bâtiments, d’autres arbres ou d’autres branches du même arbre peut inhiber la croissance).

1.2.8 Classification croisée

Un grand nombre de ces travaux sous-tendent la décomposition de l'arbre en deux structures complémentaires. La structure topologique matérialisera l'organisation interne des branches d'un arbre à l'exclusion de toute considération géométrique. La structure géométrique inclura toutes les informations géométriques concernant l'arbre (positions des nœuds, épaisseur des branches,...).

Dans les paragraphes suivants nous présentons ces travaux selon une classification transversale en fonction des trois aspects :

- Topologie : La structure topologique d'un arbre représente son architecture interne et exclut tout caractère géométrique. Quand elle existe, elle est représentée par un objet mathématique (mot,…).

- Géométrie : Elle consiste en le plongement de l'arbre topologique dans le plan ou dans l'espace.

- Rendu : Il traite du type de rendu obtenu et donc de toutes les techniques infographiques utilisées pour arriver à ce rendu (élimination des parties cachées, plaquage de texture).

Cette décomposition est classique en modélisation et en informatique graphique, elle est employée dans les travaux présentés dans les chapitres suivants pour la modélisation et le dessin d'arbres botaniques et de reliefs montagneux.

1.2.8.1 La topologie

La topologie va être ici vue sous deux aspects :

- Est-elle ou n'est-elle pas présente dans le modèle?

- Est-elle ou n'est-elle pas utilisée pour paramétrer la forme finale de l'arbre obtenue par ce modèle?

1.2.8.2 La géométrie

Le classement des méthodes géométriques va être effectué en fonction du type de modélisation, c'est à dire, "quel espace de travail a été employé?" et "dans cet espace quelles sont les primitives utilisées?". On trouve en effet des méthodes relativement classiques modélisant les objets dans un espace euclidien à partir d'angles d'embranchement, de longueurs et d'épaisseurs attribués aux arêtes, au moyen de primitives comme des lignes, des cylindres,..., mais aussi des méthodes beaucoup moins classiques tant pour l'espace de travail que pour les primitives utilisées sur cet espace.

1.2.8.3 Le rendu

Les méthodes de modélisation décrites dans les paragraphes précédents génèrent des structures qu'il reste maintenant à dessiner. Les particularités de ces structures (type, nombre d'éléments les composant) ont une influence sur les algorithmes qu'il est possible ou qu'il n'est pas possible d'employer. Dans certain cas de nouveaux algorithmes ont même dû être définis.

1.3 Les reliefs

La simulation réaliste de scènes naturelles est l'un des domaines de l'infographie où se posent les problèmes les plus difficiles en raison de la complexité des scènes et des phénomènes à modéliser. Un paysage est composé d'un ensemble d'objets naturels et artificiels de natures différentes dont la modélisation individuelle est difficile. Parmi ces objets on trouve bien sûr les arbres, mais aussi les nuages, les bâtiments et surtout le relief qui les supporte. La composition de ces objets au sein d'une scène est aussi un problème compliqué.

Les méthodes imaginées pour la génération de reliefs sont beaucoup moins variées que celle traitant de la modélisation des arbres.

Les domaines d'application de la modélisation de relief sont nombreux (simulateurs de vols, animation, images de synthèse, ...) et imposent deux objectifs antinomiques : le réalisme et l'efficacité. Peu de modèles concilient ces deux contraintes : ceux utilisés dans les applications "temps réel" (comme les simulateurs de vol) sacrifient le réalisme à l'efficacité, les modèles au rendu plus réaliste peuvent demander des temps de calcul très importants (plusieurs heures).

Les techniques développées en modélisation et rendu de terrain peuvent être classées en un certain nombre de catégories.

1.3.1 Les techniques à base de plaquage de texture

Historiquement les plus vieilles techniques de modélisation de relief sont celles basées sur le plaquage de texture sur des primitives graphiques simples.

Dungan, Stenser, Sutty [DS78] produisent des images 2D de terrains par plaquage de texture sur des zones de l'image.

 Marshall, Wilson et Carlson [MW80] utilisent des modèles procéduraux de manière à décrire les hiérarchies présentes à l'intérieur d'une scène (arbre -> forêt d'arbres, montagne -> chaîne de montagnes, forêt d'arbres + chaîne de montagnes -> paysage, ...) et à rendre ainsi plus facile le travail de conception et de dessin d'une telle scène. Chacun des éléments de base (arbre, colline, ...) est entièrement décris par un ensemble de paramètres permettant la modélisation de l'objet. Typiquement ces valeurs seront les paramètres de la procédure (au sens informatique) permettant la conception et le dessin de cet objet. Dans le cas particulier de la génération de collines, un logiciel interactif à été écrit pour la conception d'un maillage topographique. Des opérations géométriques élémentaires permettent la paramétrisation de ce relief.

Gardner [Ga84] modélise un terrain et plus généralement un paysage composé (relief, arbres, nuages) par un ensemble de surfaces quadriques 3D (équation cartésienne générale de cette famille de surfaces: Q1x2+Q2y2+Q3y2+Q4xy+Q5yz+ Q6zx+Q7x+Q8y+Q9z+Q0 = 0). Dans la pratique Gardner utilise surtout des hyperboloïdes et des ellipsoïdes. Pour obtenir une plus grande variété topographique et éviter des problèmes de recoupement entre surfaces qui pourraient être coûteux en temps de calcul, chacune de ces surfaces quadriques peut être limitée par un ou plusieurs plans. Pour réaliser l'affichage d'une scène, Gardner gère un éclairage et plaque sur ces surfaces une texture calculée mathématiquement. L'utilisation d'une texture mathématique a pour buts :

- l'obtention d'un rendu réaliste (le plaquage de texture est nécessaire pour le terrain et impératif pour les nuages et les arbres),

- la réalisation de gros plans,

- la réalisation d'une animation.

Kaneda, Kato, Nakamae, Nishita, Tanaka, Noguchi [KK89] utilisent aussi une méthode par plaquage de texture, mais dans un but différent : la synthèse d'images artificielles de zones géographiques existantes et dont on dispose de relevés topographiques et de photographies aériennes. Ils opèrent en six étapes.

a) Saisie des lignes de niveau d'une carte topographique.

b) Génération d'une carte 3D par maillage à partir des lignes de niveau. Il ne s'agit pas ici d'un maillage classique triangulaire ou carré mais d'un maillage radial dépendant de la position de l'observateur. Du point de vue de l'observateur, le maillage ainsi obtenu possède des facettes quadrangulaires ayant deux cotés verticaux.

c) Ajustement de la teinte de photographies aériennes de la zone à représenter.

d) Plaquage de ces photographies en tant que texture sur les facettes.

e) Pour tenir compte des arbres, modification du modèle, par rehaussement des facettes contenant des arbres et ajout de nouvelles facettes verticales à la limite des zones forestières. Une texture spéciale est plaquée sur les facettes ajoutées.

f) Introduction des constructions et gestion des ombres portées.

L'inconvénient conceptuel principal de ces méthodes est qu'elles n'incluent pas un réel mécanisme de génération automatique de relief.

1.3.2 Les méthodes fractales

La seconde catégorie de méthodes de génération de reliefs est basée sur la théorie mathématique des fractales de Mandelbrot [Ma82].

Une approche intuitive et très connue consiste à considérer qu'une fractale est la transformation récursive d'un objet par n copies de lui même à l'échelle r. C'est ce que l'on appelle l'autosimilarité. La figure 1R présente des exemples de transformations en dimension 1. Il est bien entendu possible d'opérer dans un espace de dimension quelconque et, en particulier pour les reliefs, en dimension 2. On a coutume de caractériser un objet fractal à partir d'un paramètre numérique généralement noté D appelé dimension fractale. D est égal à et caractérise la manière selon laquelle une fractale évolue dans l'espace où elle est dessinée.

Les fractales stochastiques, par opposition aux fractales déterministes, permettent de générer des dessins non réguliers. On obtient de bons résultats avec D voisin de 1,2 pour générer des rivages océaniques (lignes) et avec D voisin de 2,2 pour la génération de montagnes (surfaces), plus D croit plus la ligne ou la surface devient chaotique et irréaliste.

Figure 1R : Fractales déterministes

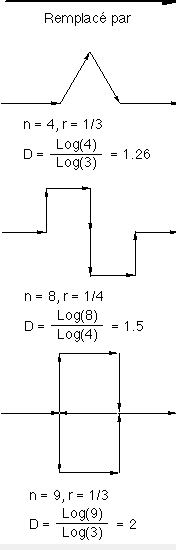
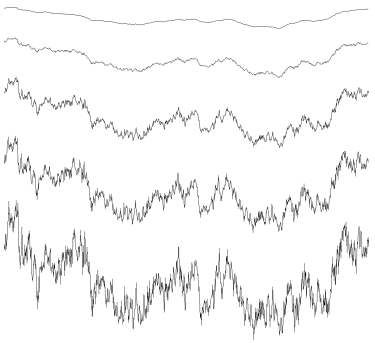Figure 1R' : Mouvement Brownien fractionnaire avec des valeurs de H égales à 0.2, 0.3, 0.4, 0.6 et 0.8 de haut en bas correspondant à des valeurs de D égales à 1.8, 1.6, 1.4, 1.3 et 1.2.

La théorie des fractales est issue de travaux de Mandelbrot et van Ness [MV68] où est introduit la notion de mouvement Brownien fractionnaire (fractional Brownian motion, fBm) pour caractériser une famille de processus stochastiques Gaussiens unidimensionnels VH(t) (H représente un paramètre numérique compris entre 0 et 1 et t représente le temps) tels que plus H est proche de 0 plus la courbe est bruitée (Figure 1R'). Une valeur de H égale à 0,5 quantifie une mouvement Brownien normal. L'une des propriétés de ces processus temporels est l'autoaffinité, c'est à dire que deux morceaux quelconques de la courbe représentative du processus se ressembleront, mais surtout, si l'on effectue une mise à l'échelle d'un facteur r sur le temps et d'un facteur rH sur VH(t), la courbe garde toujours le même aspect.

L'extension multidimensionnelle des fBm permet de modéliser un large éventail de phénomènes naturels dont, en particulier, les reliefs. Le paramètre temps t est alors transformé en un couple (x,y) indiquant une position dans le plan d'un point P, VH(x,y) donne l'altitude du point P (Figure 1R''). Un objet fractal de dimension fractale D peut apparaître comme un fBm de coefficient H tel que D = E + 1 - H où E est le nombre de variables de la fonction fBm, c'est à dire la dimension euclidienne de l'objet construit. Cet objet n'est évidemment pas strictement autosimilaire mais seulement autoaffine.

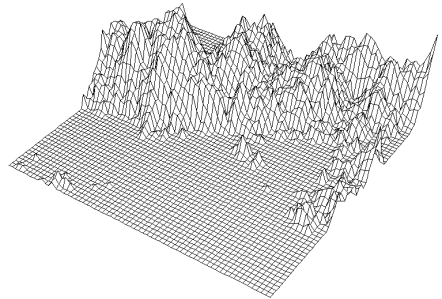
Figure 1F'' : Un relief fractal généré par fBm représenté par facettes

Les méthodes fractales sont présentées sous un certain nombre d'aspects (mathématique, programmation, applications) par Barnsley, Devaney, Mandelbrot, Peitgen, Saupe et Voss dans [BD88] et dans bien d'autres ouvrages ([Ba88], [Fa90],...). La propriété d'autosimilarité peut être traduite au moyen d'un grand nombre de formalisations mathématiques. la plus connue est probablement celle permettant de générer les ensembles de Julia-Fatou et de Mandelbrot : x -> x2 + c, où x est une variable complexe et c est une constante complexe.

De très nombreux travaux ont été effectués avec pour but une implantation efficace des fractales stochastiques. En effet, la programmation exacte des lois mathématiques mises en œuvre requiert une quantité de calcul très importante. Ces implantations sont essentiellement des approximations du mouvement Brownien fractionnaire soit par des techniques spatiales (subdivision récursive), soit par des techniques spectrales (par filtrage de Fourier).

Figure 1S : Une étape de fractalisation d'un triangle

Fournier, Fussel et Carpenter [FF82] présentent des techniques de subdivision récursive qui peuvent être utilisées pour construire des lignes polygonales fractales (approximation de la forme de l'Australie à partir d'un octogone), des pavages polygonaux fractaux ou des surfaces paramétriques stochastiques indépendants du repère cartésien de l'espace de travail (Figure 1S). Smith [Sm84] présente les techniques de subdivision de Fournier et al. en terme de grammaire et de règles de réécriture (Graftals) appliqués à des cartes topologiques. Miller [Mi86] aborde le problème du choix du motif de subdivision récursive en soulignant que ce choix influe sur l'aspect final du dessin (on peut reconnaître le motif à partir de l'image obtenue). Deux exemples de subdivision sont décrit (en triangle et en diamant) qui peuvent poser problème, et une meilleure solution est proposée par décomposition en carrés. Enfin, il donne une solution au problème du rendu d'un paysage fractal par un algorithme parallèle de ray tracing.

Figure 1S' : Un nuage fractal

Les méthodes fractales sont très souvent considérées comme les plus efficaces pour la création d'images réalistes d'objets naturels (images de Voss [Vo83] et de Cook, Carpenter, Porter, Reeves, Salesin, Smith [CC83]). Les qualités de l'approche fractale s'expriment en termes de réalisme remarquable, de très importante amplification des données (un très petit nombre de paramètres suffit à décrire un nuage ou une montagne fractale simple) et de niveau de détail aussi fin que voulu (un nuage est donné Figure 1S', une montagne fractale peut être trouvée page 249 de [BD88]). Certains inconvénients ont toutefois été signalés. Par exemple, l'effet de plissement ou "creasing effect" est lié à l'indépendance du contexte des grammaires précitées. Benoit Mandelbrot dans [BD88] (Annexe A) cite un autre problème qui définit assez bien les questions qui sont abordées par une approche non fractale dans la deuxième partie de cette thèse :

"The most basic defect of past fractal forgeries of landscape is that every one of them fails to include river networks. This is one reason why these forgeries look best when viewed from a low angle above the horizon, and are worst when examined from the zenith. This is also why achieving a fully random combined model of rivers and of mountains will be a major advance for computer graphics (and also perhaps for the science of geomorphology)."

Une autre façon d'exprimer ce problème est de constater que dans les images fractales de montagnes, vallées et montagnes sont symétriques, ceci étant dû à la symétrie de la loi gaussienne utilisée, alors que dans la réalité, la montagne et son fleuve présentent une totale dissymétrie due à l'érosion. De plus, les fractales ne sont pas capables de modéliser directement un réseau fluvial dans sa totalité. Il serait illusoire de penser qu'un seul modèle global puisse rendre compte de la très grande diversité des processus mis en œuvre au cours de la génération d'un relief (soulèvements dus à la tectonique, érosion par les rivières, les glaciers, le vent, le gel, ..., présence de strates géologiques, formation de bassins sédimentaires par accumulation de matériaux détritiques dans les vallées,...). Mandelbrot ébauche à ce problème un type de solution (voir [BD88]) qui consiste dans un premier temps, à construire récursivement, simultanément deux fractales déterministes représentant le réseau fluvial et le réseau des lignes de partage des eaux, puis dans un deuxième temps, à relever le relief le long des lignes de partage des eaux par une technique de subdivision récursive modifiée pour tenir compte des problèmes d'altitude (maxima pour les sources, diminution de l'altitude le long des fleuves,...).

1.3.3 Les techniques basées sur un modèle d'érosion

La démarche qui consiste à générer un relief par simulation de l'érosion (modèle dynamique) ou par utilisation de lois rendant compte des conséquences de l'érosion sur un bassin de drainage (modèle statique) caractérise la troisième catégorie de techniques de modélisation de terrain.

1.3.3.1 Méthodes statiques

Outre la solution sus-mentionnée de Mandelbrot, les travaux de Kelley, Malin et Nielson [KM88] sont caractéristiques de cette approche. La description du bassin fluvial (fleuve et bassin de drainage) est fondée sur des modèles empiriques d'écoulement utilisés en géomorphologie (voir Abrahams [Ab80], Howard [How71], Shreve [Sh66]) mettant en œuvre un arbre binaire recouvrant une carte modélisant le réseau hydrographique et le bassin de drainage associé. Cet arbre est généré par ajouts récursifs d'affluents à partir d'une arête racine unique concurremment à l'ajout de facettes à la carte sous-tendue.

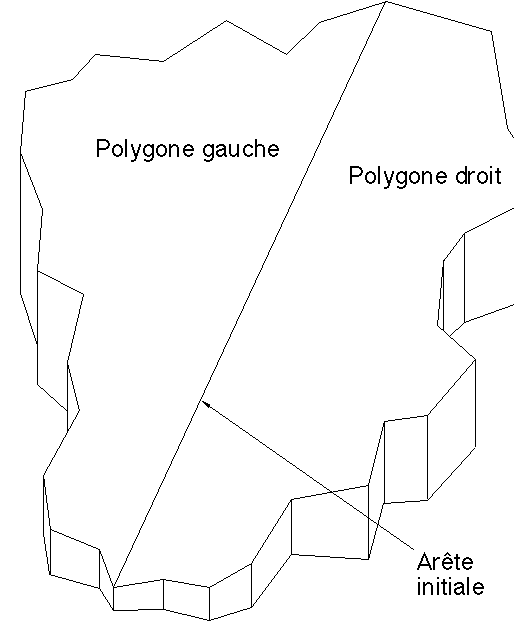
Figure 1T: Système de drainage initial

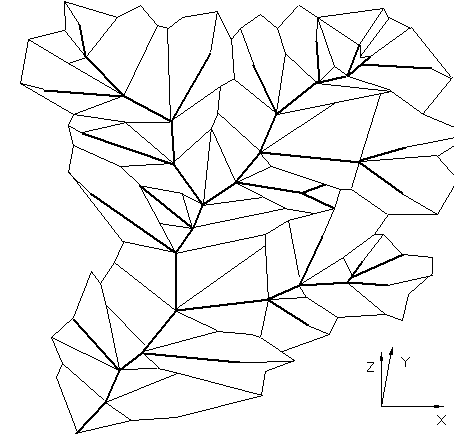
Figure 1T' : Maillage modélisant un relief

L'arête racine est initialement placée à l'intérieur d'un système de drainage initial défini par l'arête initiale et les deux polygones à droite et à gauche de cette arête (Figure 1T), ces trois composants étant positionnés dans R3. La création d'un affluent sur un segment de rivière intervient si le rapport :

r= est supérieur à une limite donnée. Il y a alors création de deux nouveaux nœuds : un nœud de jonction sur l'ancien segment et un nœud à l'extrémité du segment nouvellement créé. La carte est elle-même modifiée par création de nouvelles facettes. Le placement géométrique des deux nouveaux nœuds est effectué en fonction de contraintes géomorphologiques qui vont permettre de décider du coté d'insertion du segment (le coté où le rapport r est le maximum) et de calculer les positions des nœuds en x en y et en z (Figure 1T').

Les modélisations topologiques et géométriques (plongement dans R3) sont ici effectuées simultanément avec une influence de la géométrie sur la topologie.

Le maillage polygonal obtenu est alors interpolé par une surface analogue à une surface spline sous tension pour permettre d'attribuer une altitude à n'importe quel point du relief et ainsi générer un nouveau maillage triangulaire régulier en projection sur xOy de la surface modélisée (Figure 1T'').

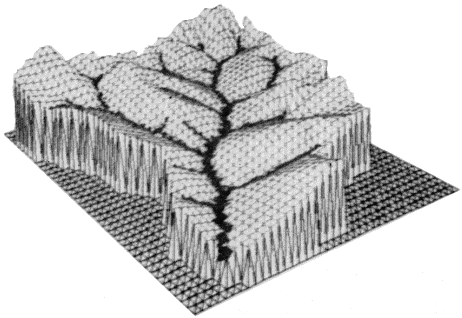
Figure 1T'' : Un relief par modèle d'érosion (Illustration extraite de [KM88], p 267 , © ACM.)

Les images finales sont obtenues en attribuant une couleur à chaque facette. Cette couleur est fonction de paramètres tels que la position, l'altitude ou la pente de la facette. L'image de relief montrée à la figure I. compte environ 40000 triangles pour un temps de modélisation de 8 minutes (sur SUN 3) et un temps d'affichage de 4 minutes sur VAX 11/750.

Cette méthode matérialise un modèle de génération statique, c'est à dire qu'il n'y a pas simulation de l'érosion par déplacement de matière, mais génération d'un relief à partir des conséquences d'un phénomène d'érosion présentées sous forme de lois topologiques et géométriques.

1.3.3.2 Modèles dynamiques

Les modèles dynamiques de génération de reliefs de Roudier [Ro91] et Musgrave, Kolb et Mace [KMK89] modélisent en revanche l'évolution d'un relief au moyen de processus mettant en œuvre des déplacements de matière.

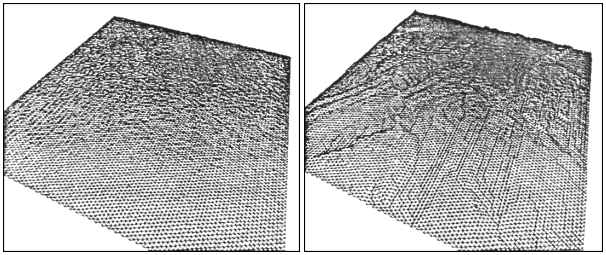
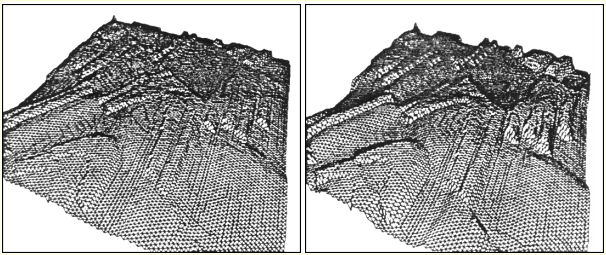
Roudier [Ro91], partant d'un maillage régulier initial carré ou hexagonal dont chaque sommet est affecté d'une altitude constante bruitée fractalement, simule l'évolution dans le temps de ce relief en faisant subir à chaque itération temporelle à chaque point du maillage une érosion exprimée par une baisse de son altitude (dans certains cas particulier de points situés dans une cuvette, il peut y avoir accroissement de l'altitude par sédimentation). Cette variation d'altitude est calculée à partir d'un certain nombre de lois simulant un déplacement de matière traduisant l'action de l'eau :

- Loi gravitaire : Elle traduit le déplacement lent des terrains dans le sens de la pente sous l'action de la gravitation et entraîne une diminution d'altitude Zg (valeur négative).

- Loi mécanique : Elle rend compte de l'usure des sols avec production de matériaux détritiques (sédiments) sous l'action des eaux de ruissellement provenant des précipitations. Les eaux de ruissellement passant sur chaque nœud du maillage sont la somme des précipitations sur ce nœud et des eaux de ruissellement provenant des sommets adjacents de plus haute altitude, diminuée des quantités d'eau infiltrée et évaporée. Les matériaux détritiques sont déplacés vers le nœud adjacent d'altitude la moins élevée. La loi mécanique entraîne une diminution d'altitude Zw (valeur négative).

- Loi chimique : Elle permet de calculer la fraction des matériaux rocheux mis en solution par les eaux d'infiltration et qui disparaissent de la simulation. Elle se traduit par une diminution d'altitude Zc (valeur négative).

- Loi sédimentaire : Quand l'érosion mécanique amène des matériaux détritiques dans une cuvette ou que la concentration de ces matériaux dans les eaux de ruissellement devient trop importante vis à vis de la pente, il y a sédimentation, phénomène qui entraîne une prise d'altitude Zd (valeur positive).

La différence d'altitude Z à chaque itération t de la simulation pour chaque nœud n du maillage et donc Z(t,n) = Zg(t,n) + Zw (t,n)+ Zc(t,n) + Zd(t,n).

Figure 1U : Evolution d'un relief (Images extraites de [Ro91]).

Ces quatre lois sont fonctions des précipitations et de paramètres géologiques attribués aux nœuds :

- un coefficient Kd de dureté de la roche,

- un coefficient Kf d'infiltration,

- un coefficient Kv de végétation,

- un coefficient Kc de dissolution chimique,

- un rapport entre les sédiments déposés et les sédiments restant en suspension.

Le calcul de l'écoulement de l'eau est effectué de manière simplifiée en considérant que les eaux de ruissellement provenant d'un sommet du maillage quelconque se dirigent toujours vers le sommet d'altitude minimum qui lui est adjacent. Il faut bien entendu que ce point ait une altitude inférieure à celle du point source sinon il y création d'un lac. Ce processus d'écoulement permet de tracer les cours d'eau présents à l'intérieur du relief.

La simulation est assez poussée dans le sens où une véritable modélisation géologique du sous-sol du terrain initial est définie avec le calcul possible pour tout point du maillage polygonal, quels que soient sa position et surtout son altitude, d'un ensemble complet de paramètres géologiques (modélisation du sol et du sous-sol par modélisation préalable de phénomènes géologiques tels que les plissements ou l'apparition de failles). En fonction de ces caractéristiques l'érosion est différente suivant la position des nœuds du maillage. On voit ainsi ressortir les caractéristiques du sous-sol (résistance plus ou moins grande à l'érosion, lignes de failles) au fil des itérations rythmant l'écoulement du temps (Figure 1U).

Musgrave, Kolb et Mace [KMK89] résolvent le problème de la symétrie des vallées et des montagnes dans un paysage généré par une méthode fractale en effectuant une modélisation en deux étapes consécutives :

- une génération fractale adaptée à la génération de reliefs,

- une phase d'érosion du relief fractal obtenu.

La génération fractale est effectuée en faisant varier les paramètres caractéristiques suivants :

- la dimension fractale,

- "l'échelle de croisement" (crossover scale) qui représente la valeur d maximale telle qu’un déplacement d’une distance d dans le plan horizontal puisse être accompagné d’une différence d’altitude de même valeur d.

Ces deux paramètres varient en fonction de la position considérée dans le plan et de l'altitude :

- On se servira de la dimension fractale de manière à rendre les reliefs générés moins chaotiques dans les zones basses. La figure 1V montre un exemple de relief où la dimension fractale augmente de 2 à 3 de la gauche vers la droite

Figure 1V : Influence de la dimension fractale (Illustration extraite de [KMK89], p 48, © ACM.)

- Le paramètrage de l'échelle de croisement permet de définir des zones où l'amplitude du relief est plus ou moins importante La figure 1V' montre une ligne de crête où l'échelle de croisement varie en fonction de l'altitude et de la position horizontale.

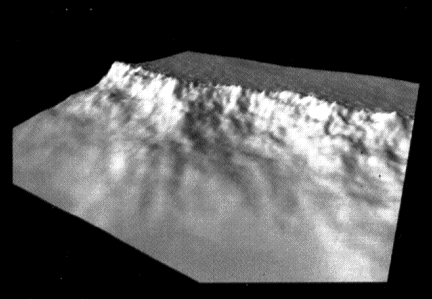
Figure 1V' : Influence de l'échelle de croisement (Illustration extraite de [KMK89], p 48, © ACM.)

L'utilisation de ces deux paramètres est nécessaire car la dimension fractale ne suffit pas à caractériser correctement un terrain. Par exemple une piste d'atterrissage d'un aéroport et la chaîne himalayenne possèdent la même dimension fractale et pourtant ne se ressemblent pas car leurs échelles de croisement sont respectivement de l'ordre du millimètre et de l'ordre du kilomètre (voir [Ma82]).

Après la génération fractale on obtient un relief modélisé par facettes pouvant être vu comme une carte plongée dans R3. Pour résoudre le problème de l'absence de modélisation réelle des réseaux fluviaux, une phase d'érosion hydraulique est ajoutée à la suite de la génération fractale, de manière à simuler des déplacements de matière. Pour cela, à chaque itération du processus discret d'érosion, chaque facette du relief va être traitée pour évaluer la quantité de sédiments qui précipite ou qui est érodée. Cette quantité est fonction d'un certain nombre de valeurs :

- la quantité d'eau provenant des précipitations et des facettes adjacentes à cette facette (fonction des altitudes relatives de ces facettes par rapport à la facette testée),

- la quantité de sédiment arrivant avec l'eau de ruissellement provenant des facettes adjacentes,

- la constante Kc définissant la quantité maximale de sédiment pouvant être en suspension dans un volume d'eau, la constante Ks définissant la solubilité du sol de cette facette, la constante Kd définissant la vitesse de sédimentation.

Du point de vue de la simulation du processus d'érosion hydraulique, les travaux de Musgrave et al. semblent une version simplifiée de ceux de Roudier. De plus il n'y a pas de modélisation géologique du sous-sol. La modélisation fractale initiale permet d'apporter des détails aux reliefs qui n'apparaîtraient pas sans, cela semble être une bonne méthode pour calculer le relief de départ.

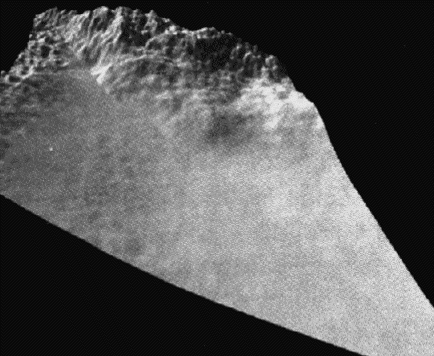
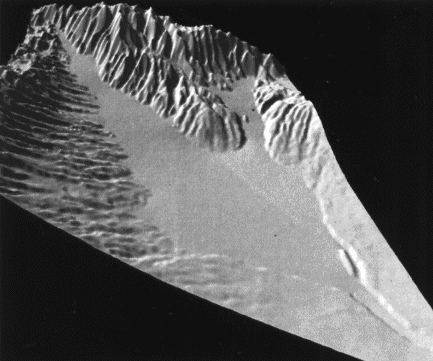
Figure 1W : Une vallée sans et après une très longue érosion ([KMK89], p 48 et 49, © ACM).

Les travaux de Musgrave et al. sont axés sur un troisième aspect : le rendu au moyen d'un algorithme spécifique de lancé de rayons qui ne sera pas décris ici.

1.4 Conclusion

La conclusion de cette étude comparative est la très grande diversité des modélisations proposées dans le cadre de la synthèse d'images de végétaux et de terrains. Il serait intéressant de rechercher un modèle qui généralise et unifie, en particulier pour les végétaux, ces différentes approches.