Chapitre 2
Cartes et arbres
2 Cartes et arbres
2.1 Introduction
Les modèles de synthèse d'image de végétaux et de bassins montagneux sont fondés sur les structures d'arbre binaire pour les végétaux, d'arbres binaires planaires et de cartes planaires pour les bassins fluviaux. Ces fondements sont d'une double nature :
1) Au niveau algorithmique, nous utiliserons les structures de données, les algorithmes classiques de parcours et de traitement de ces objets. Aussi rappelons nous ici les principales définitions concernant arbres et cartes planaires, du point de vue topologique, combinatoire (voir [Co75]), et structures de données, et les liens entre ces différents niveaux d'appréhension de ces objets. On admettra cependant connues les notions classiques sur les graphes (définition, chemin,..., voir par exemple Berge [Be70]).
2) Au niveau modélisation, nous serons amenés à utiliser certains algorithmes de plongement automatique d'arbres planaires, à les modifier et à proposer de nouveaux algorithmes de plongement automatique de cartes planaires. Aussi étudions nous dans la suite de ce chapitre, en les classant en fonction de leurs capacités à prendre en compte des contraintes graphiques de plus en plus sophistiquées, quelques algorithmes de plongement automatique d'arborescences planaires ([WS79], [RT81]), et de cartes planaires (cf chapitre 5, partie 2).
2.2 Cartes
Les cartes topologiques ont été étudiées dans les années 60 du point de vue combinatoire par Tutte (voir [Tu68], [Tu84], par exemple) , Walsh ([WL72a,b]),.... Les problèmes posés sont alors l'énumération des familles de cartes en fonction de certains critères, par exemple: combien y a-t-il de cartes planaires à n sommets et m faces?, avec en arrière pensée la résolution du problème des quatre couleurs, pour lequel un algorithme a été proposé depuis par Appel et Haken en 1979, selon une toute autre méthode que celle purement combinatoire espérée par Tutte. Cette recherche se heurte rapidement a la complexité des calculs formels qu'elle nécessite (voir par exemple [Tu68]) et seules les cartes planaires conduisent à des résultats explicites, les cartes de genre 1 et plus résistant à toute énumération. Les travaux de Cori dans les années 70 (voir par exemple [Co75]) ont considérablement développé l'aspect théorie des langages de cette étude des cartes planaires. C'est la notion de carte combinatoire (introduite par Edmonds) qui est au départ de ces développements. Cori propose ainsi un codage des hypercartes combinatoires planaires par un langage sur un alphabet infini, codage qui lui permet de traduire les problèmes d'énumération de cartes en des problèmes de résolution d'équations intégro-différentielles dans l'algèbre large du monoïde libre. Cette approche lui permet aussi d'aborder certains problèmes informatiques liés aux graphes, comme celui du dessin automatique de cartes planaires (cf [CH75]). A la suite des travaux de Cori, de nouveaux résultats ont été obtenus (voir par exemple [Ar85a,b], [Ar87a,b], [AJa91], [AJO91], [BC87a], [BC87b], [BC88], [Ja91]) sur l'énumération des cartes de genre supérieur à 0.
La notion de carte combinatoire semble pouvoir être un outil puissant dans le choix de bonnes structures de données adaptées à nombre de problèmes de toute nature liés aux graphes: celui du dessin de graphes planaires, de circuits intégrés, mais aussi celui du dessin de végétaux et de la généralisation en dimensions supérieures des subdivisions de l'espace (cf par exemple [Li87], [LF87], [Li88], [Li89], [AK89]).
Nous présentons ici les définitions et les liens entre les notions de carte topologique et de carte combinatoire, et la structure de données informatique à la base des modélisations des chapitres suivants. Nous nous restreindrons au cas planaire dans la suite.
2.2.1 Carte topologique planaire
Définition
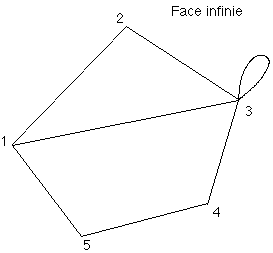
Figure 2A : Carte planaire c
On appelle carte planaire topologique c une partition de la sphère de R3 en trois ensembles finis de cellules (Figure 2A) :- l'ensemble des sommets de c qui est un ensemble fini de points,
- l'ensemble des arêtes de c qui est un ensemble fini d'arcs ouverts simples de Jordan, deux à deux disjoints, dont les extrémités (confondues ou non) sont des sommets,
- l'ensemble des faces de c qui sont des domaines simplement connexes, dont les frontières sont des réunions de sommets et d'arêtes.
On représentera dans la suite ces cartes dessinées sur la sphère par projection stéréographique sur le plan à partir d'un point intérieur à l'une des faces qui devient la face infinie de la carte dans sa représentation sur R2.
Une carte planaire topologique est donc une représentation topologique planaire d'un graphe non orienté connexe.
2.2.2 Carte combinatoire
La manipulation des cartes topologiques dans leur présentation purement géométrique n'est pas aisée pour certaines applications, comme par exemple le dessin automatique de cartes ou l'étude combinatoire des cartes. Nous présentons ici un autre mode de représentation des cartes dans lequel, à l'aspect topologique est substitué une représentation purement algébrique.
On appelle brin (ou arc) une arête orientée de la carte et on note B l'ensemble des brins. A tout brin est associé de manière évidente, son sommet initial, son sommet final, l'arête qui constitue son support et son brin opposé.
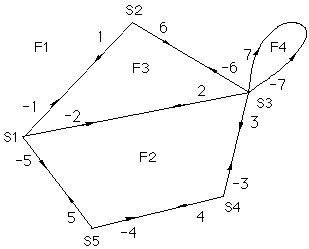
Figure 2B : Carte topologique
S
i la carte c contient n arêtes, on numérote ses brins au moyen des entiers de l'ensemble Zn = {-n, -(n-1), ..., -1, 1, 2, ..., n} de façon à ce que deux brins opposés aient des numéros opposés (Figure 2B). On confond alors les ensembles B et Zn.On définit la permutation a sur B qui à tout brin b associe son brin opposé. a est une involution sans point fixe dont les cycles sont bijectivement associés aux arêtes de la carte. Dans la carte de la figure 2B : a = (1,-1), (2,-2), (3,-3), ..., (7,-7).
On note s la permutation sur B qui à tout brin b associe le premier brin rencontré en tournant autour du sommet initial de b dans le sens positif choisi sur le plan (le sens contraire des aiguilles d'une montre dans la suite). Les cycles de s sont bijectivement associés aux sommets de la carte. Dans la carte de la figure 2B : S1 = (-5, -2, -1), S2 = (1, 6), S3 = (-6, 2, 3, -7, 7), S4 = (-3, 4) et S5 = (-4, 5).
On note ![]() la permutation s o a sur B. Les cycles de
la permutation s o a sur B. Les cycles de ![]() sont les circuits orientés
constituant les frontières des faces topologiques de la carte. Les cycles de
sont les circuits orientés
constituant les frontières des faces topologiques de la carte. Les cycles de ![]() sont
donc bijectivement associés aux faces de la carte. Dans la carte de la figure 2B : F1 = (-5,-4,-3,-7,1,-6), F2 =
(-2,3,4,5), F3 = (-1,6,2), F4
= (7).
sont
donc bijectivement associés aux faces de la carte. Dans la carte de la figure 2B : F1 = (-5,-4,-3,-7,1,-6), F2 =
(-2,3,4,5), F3 = (-1,6,2), F4
= (7).
Les permutations a et s ainsi définies possèdent la propriété P suivante, qui est conséquence de la connexité de c:
P : Le groupe <a,s> engendré par {a,s} (dans le groupe symétrique sB) opère transitivement sur B.
Définition
Le triplet C = (B,a,s) muni de la propriété P constitue la carte combinatoire de la carte topologique c dont il est issu.
2.2.3 Genre d'une carte combinatoire
Si t est une permutation sur B, on note z(t) le nombre de cycles de t.
Définition
C = (B,a,s) étant une carte combinatoire connexe, g(C) = 1 + ![]() est appelé le genre de la carte
combinatoire C.
est appelé le genre de la carte
combinatoire C.
Dans l'exemple de la figure 2B, g(C) = 1 +
Le genre g(c) d'une carte combinatoire est un entier naturel (voir [Co75] pour la démonstration).
Nous avons associé une carte combinatoire C à toute carte topologique planaire
c. Réciproquement, on doit à Edmonds [Ed60] le :Théorème
Pour toute carte combinatoire C de genre 0, il existe une carte topologique planaire c de carte combinatoire associée C.
On a ainsi une identité complète entre les deux notions de carte planaire topologique et de carte combinatoire de genre 0.
2.2.4 Carte planaire pointée
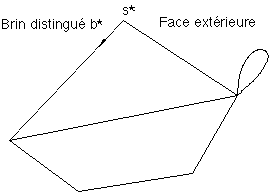
Figure 2C : Carte pointée
Une carte planaire est dite pointée si un de ses brins b* est choisi. Le brin b* est appelé brin distingué de la carte (marqué d'une flèche dans les représentations topologiques de la carte, voir figure 2C). Son sommet initial s* est appelé sommet distingué de la carte. Dans la représentation combinatoire d'une carte, le brin distingué est habituellement le brin 1 de Zn.On appelle alors face extérieure de la carte la face qui est incidente au brin distingué b* et est située à droite de b* dans le sens de son parcours. Dans la représentation usuelle d'une carte planaire pointée dans le plan, le dessin (la projection stéréographique) est réalisé de sorte que la face extérieure de la carte soit la face infinie dans le plan.
Structure de données de codage des cartes
La structure de données utilisée doit répondre à un certain nombre d'impératifs :
- Elle doit permettre le codage d'une carte très importante (plusieurs milliers de nœuds, d'arêtes et de facettes).
- Elle doit rendre facilement implantables les opérations de base s et a et par composition de celles-ci, des opérations telles que l'ajout d'un nœud ou d'une arête dans une carte.
- Elle doit rendre possible et efficace la suppression de sommets et d'arêtes.
Une représentation par pointeurs de type liste des nœuds avec une liste bouclée des brins pour chaque nœud a été choisie pour ces raisons. Ce qui donne avec un codage du type de celui du langage C :
STRUCT SOMMET {
STRUCT SOMMET *SOMMET_SUIVANT ;
STRUCT BRIN *PREMIER_BRIN ; }
STRUCT BRIN {
STRUCT SOMMET *SOMMET_ARETE ;
STRUCT BRIN *BRIN_SUIVANT ;
STRUCT BRIN *BRIN_PRECEDENT ;
STRUCT BRIN *BRIN_OPPOSE ;}
L'accès à la structure de données s'effectue par l'intermédiaire d'un pointeur sur un sommet qui, dans la pratique, indique le sommet distingué. Le PREMIER_BRIN du sommet distingué sera le brin distingué de la carte. Tout au long des manipulations effectuées sur la carte, on imposera de plus que le premier brin de tous les sommets du bord de la face extérieure pointe sur le sommet suivant du bord de la face extérieure dans le sens positif choisi sur la surface de manière à simplifier des opérations telles que celle de décomposition récursive de la carte en sous-cartes (les brins pointés, premiers brins d'entrée dans les sous-cartes issues de la décomposition devant rester des brins extérieurs, voir chapitre 5.
La permutation a s'implante de manière simple en utilisant le champ BRIN_OPPOSE associé à tout pointeur sur un brin. De la même manière la permutation s s'implante en utilisant le champ BRIN_SUIVANT. Le champ BRIN_PRECEDENT sera utilisé pour rendre plus aisées un certain nombre de manipulations et conserver la linéarité de certains algorithmes.
2.3 Arbres
2.3.1 Arborescence
Définition
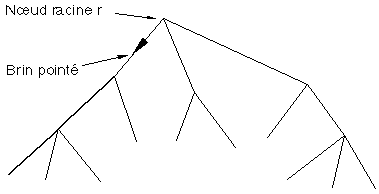
Figure 2D : Une arborescence
On appelle arborescence (appelé arbre dans la suite) toute carte planaire pointée à une seule face (la face infinie extérieure) (Figure 2D). Le sommet distingué est appelé la racine de l'arborescence. Le brin distingué de l'arborescence pointe sur le fils à gauche de la racine. A partir de l'orientation donnée par ce brin on peut retrouver le fils à gauche de n'importe quel nœud. Pour tout sommet x d'une arborescence G de racine r, il existe un chemin unique de r à x.
Les sommets de l'arborescence sont souvent appelés nœuds. Le nœud père de tout nœud x est le premier nœud, s'il existe, à partir de x sur le chemin de x à la racine de l'arborescence. Le seul nœud de l'arborescence qui n'a pas de père est donc la racine. Tous les nœuds connectés à un nœud x à l'exception du père de x sont les fils de x. Deux nœuds fils d'un même nœud père sont dits frères. Un nœud qui n'a pas de fils est appelé une feuille ou un nœud terminal. Un nœud qui a au moins un fils est un nœud interne.
Une arborescence binaire (arbre binaire dans la suite) est définie comme étant une arborescence telle que tout nœud a soit deux fils (un gauche et un droit), soit aucun.
Par la suite, la dénomination usuelle "arbre" désignera systématiquement une arborescence.
2.3.2 Structures de données usuelles de représentation des arbres
2.3.2.1 Arbres
Un arbre peut être représenté par une structure de données mettant en œuvre une gestion de la liste des fils de chaque nœud. On utilisera à cette fin la structure de données suivante utilisant des pointeurs pour chaîner le fils gauche de tout nœud et la liste des frères droits de ce fils gauche s'ils existent :
STRUCT NŒUD{
STRUCT NŒUD *FILS_GAUCHE ;
STRUCT NŒUD *FRERE_DROIT ; }
L'arbre T est alors désignée par un pointeur sur le nœud racine.
Un troisième champ contenant un pointeur sur le père du nœud considéré peut être inclus dans la structure si des retours à la racine doivent être effectués pour travailler sur la structure de données.
2.3.2.2 Arbres binaires
Dans le cas particulier des arbres binaires une simplification évidente peut être apportée à la structure de données :
STRUCT NŒUD{
STRUCT NŒUD *FILS_GAUCHE ;
STRUCT NŒUD *FILS_DROIT ; }
2.3.3 Algorithmes de dessins d'arbres
Le choix des algorithmes de dessin d'arbres et de cartes présentés ici et au chapitre 5 a été guidé par la volonté de mettre en évidence une évolution dans les contraintes de toutes natures qu'ils satisfont afin d'étudier les solutions utilisées pour la prise en compte de ces contraintes.
Les arbres sont des structures de données très communes en informatique. Ils modélisent en effet de nombreux problèmes réels. Un nombre considérable d'algorithmes fondés sur une structure d'arbre ont été conçus. Une bonne technique de dessin d'arbre est en effet souvent un guide intuitif très puissant dans la résolution d'un problème : de fait, la résolution de certains problèmes se réduit essentiellement à la découverte de l'arbre sous-jacent au problème. On constate pourtant assez peu de d'algorithmes de dessin automatique d'arbres dans la littérature.
Les algorithmes de dessin automatique d'arbres qui vont être développés ci-après présentent les contraintes esthétiques minimales suivantes :
- Les arêtes seront linéaires.
- Tout arbre est un graphe planaire : les arêtes ne doivent pas se couper en dehors de leurs nœuds extrémités.
- La notion d'arbre contient naturellement la notion de distance d'un nœud à la racine, appelée profondeur du nœud. Il est naturel d'imposer qu'un nœud ne soit pas dessiné plus près de la racine que son père.
- Le frère gauche d'un nœud n quelconque doit être dessiné physiquement plus à gauche que n par rapport à leur nœud père.
Le dessin d'un arbre revient à affecter un couple de coordonnées (x,y) à chacun de ses nœuds. Ces coordonnées entières seront calculées dans un repère orthonormé (cf figure 2E).
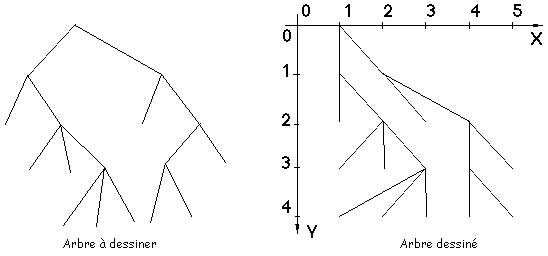
Figure 2E : Dessin simple
Tous ces algorithmes peuvent être implantés de manière à obtenir des temps d'affichage linéaires en le nombre de sommets contenus dans l'arbre dessiné.
2.3.3.1 Un algorithme simple pour le dessin d'arbres quelconques
Aucune surface de dessin n'est infinie. Les organes de sortie des systèmes informatiques sont bornés en l'une des dimensions ou même pour les deux dimensions. Deux contraintes simples sont imposées pour ce premier algorithme, permettant de tenir compte de ces limitations structurelles :
Contraintes esthétiques 1 et 2
- Tous les nœuds de profondeur identique sont dessinés sur une même ligne. Les lignes associées aux différents niveaux de l'arbre sont parallèles.
- Le dessin d'un arbre doit occuper la plus petite largeur possible.
Idée de l'algorithme
Un simple parcours en préordre (parcours prioritairement en profondeur avec traitement de tout sommet à la première visite c'est à dire avant ses propres fils) permet de calculer facilement la profondeur de chaque nœud de l'arbre (et donc son ordonnée y, cf figure 2E). Pour satisfaire la seconde contrainte, il suffit de placer chaque nœud traité le plus à gauche possible sur la ligne associée à son niveau. Pour cela, une solution simple consiste à gérer un tableau FPL des "futures positions libres", donnant pour chaque niveau la future position libre où placer le prochain nœud de ce niveau. Ce tableau sera géré au cours du parcours en préordre de l'arbre.
Algorithme
Il se résume essentiellement à la procédure PLACEMENT qui permet de calculer les deux tableaux de coordonnées X et Y (indicés sur les nœuds, initialisés à 0). FILS_GAUCHE (resp. FRERE_DROIT) est une fonction qui admet comme paramètre un nœud et qui rend en résultat son nœud fils gauche (resp. son nœud frère droit) s'ils existe ou nil s'il n'existe pas. Le tableau FPL est initialisé à 1.
Procedure PLACEMENT(N : nœud)
C : nœud
début
X[N] = FPL[Y[N]]
FLP[Y[N]] = FLP[Y[N]] +1
C = FILS_GAUCHE(N)
tant que C ? nil
Y[C] = Y[N] + 1
PLACEMENT(C)
C = FRERE_DROIT(C)
fin_tant que
fin_procedure
Les limites esthétiques de cet algorithme de dessin automatique sont clairement visibles sur la figure 2E.
2.3.3.2 Algorithme de Knuth pour le dessin d'arbres binaires
Dans l'algorithme précédent aucune contrainte n'est imposée pour la position d'un père par rapport à ses fils conduisant inévitablement à des nœuds pères situés plus à gauche que leur nœud fils gauche. L'algorithme de Knuth [Kn73] réalise le placement en x des nœuds de telle manière que tout nœud père ait une abscisse supérieure (resp. inférieure) à l'abscisse de tout nœud de son sous-arbre gauche (resp. droit), ce qui est beaucoup plus naturel.
Idée de l'algorithme
Cette contrainte est résolue en numérotant les nœuds lors d'un parcours en ordre de l'arbre binaire, parcours prioritairement en profondeur avec traitement de tout sommet après son sous-arbre gauche, mais avant son sous-arbre droit. Le parcours étant réalisé en ordre, chaque sommet a un numéro supérieur à ceux des sommets de son sous-arbre gauche et inférieur à ceux des sommets de son sous-arbre droit. Il ne reste qu'à attribuer à chaque sommet une abscisse proportionnelle à ce numéro. Un arbre binaire ainsi représenté aura la propriété visuelle intéressante de fournir par projection orthogonale de ses nœuds sur l'axe des x la suite de leurs numéros en ordre croissant (Figure 2F).
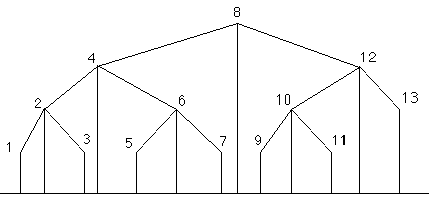
Figure 2F : Numérotation des sommets
Algorithme
Cet algorithme est implantable, comme dans le paragraphe précédent, au moyen de la seule procédure PLACEMENT permettant de remplir les tableaux de coordonnées X et Y (initialisés à 0). On utilise deux variables externes HAUTEUR et X_SUIVANT (initialisées à 0 et 1) pour gérer la coordonnée y du nœud courant dans l'arbre et son numéro d'ordre dans l'arbre.
Procedure PLACEMENT(N : nœud)
début
Y[N] = HAUTEUR
HAUTEUR = HAUTEUR + 1
si FILS_GAUCHE(N) ? nil
alors PLACEMENT(FILS_GAUCHE(N))
fin_si
X[N] = X_SUIVANT
X_SUIVANT = X_SUIVANT + 1
si FILS_DROIT(N) ? nil
alors PLACEMENT(FILS_DROIT(N))
fin_si
HAUTEUR = HAUTEUR - 1
fin_procedure
Les résultats obtenus par cet algorithme (Figure 2F) sont plus "agréables" que ceux du paragraphe précédent. La décomposition visuelle d'un arbre en ses différents sous-arbres est facile une fois le dessin effectué. L'inconvénient principal de l'algorithme de Knuth est que l'arbre dessiné est aussi large qu'il possède de nœuds.
La contrainte définie dans l'algorithme de Knuth conduit au problème que l'arbre dessiné est de largeur maximale ce qui contredit la contrainte 2. Une contrainte moins forte que celle de l'algorithme Knuth sera appliquée par la suite :
Contrainte esthétique 3
Dans l'arbre binaire dessiné, chaque fils gauche (respectivement fils droit) doit être positionné à gauche (respectivement à droite) par rapport à son père.
2.3.3.3 Algorithme de Wetherell et Shannon pour le dessin d'arbres binaires
Une nouvelle contrainte esthétique plus fine que la contrainte 3 a été introduite par Wetherell et Shannon [WS79] :
Contrainte esthétique 4
Un nœud père doit être centré par rapport à ses fils.
Idée de l'algorithme
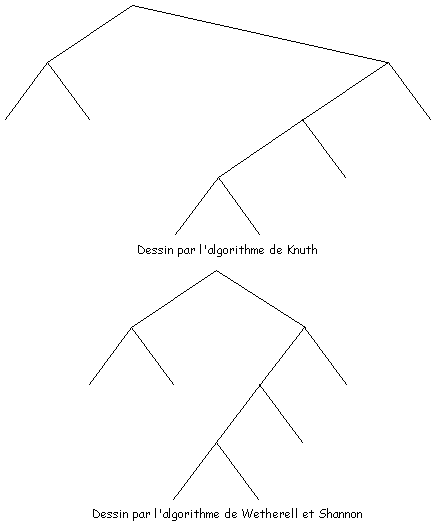
Figure 2G : Amélioration du dessin apportée par Wetherell et Shannon
Comme dans le premier algorithme un tableau PLACE_SUIVANTE fournit la prochaine position libre pour chaque niveau de l'arbre. Si ce nœud est une feuille, il est correctement placé car la nouvelle contrainte ne joue pas (ce nœud n'a pas de fils). En revanche, placer automatiquement un nœud interne au niveau h à l'abscisse PLACE_SUIVANTE[H] peut violer la contrainte définie ci-dessus. Une place (place_candidate) pour ce nœud interne satisfaisant cette contrainte, serait l'abscisse moyenne de celle de ses deux fils (ceci entraîne que le parcours prioritairement en profondeur utilisé pour affecter les coordonnées aux nœuds traitera chaque nœud en postordre, c'est à dire après les appels récursifs pour ses deux fils. Mais cette place présente l'inconvénient qu'un fils gauche déjà placé peut tendre à tirer son père trop loin vers la gauche, provoquant ainsi une collision avec le sommet de même niveau à gauche du père. La place qui sera attribuée au sommet à placer sera donc la plus grande des deux abscisses PLACE_SUIVANTE[H] et PLACE_CANDIDATE. Si l'abscisse ainsi obtenue est supérieure à la place candidate, le sous-arbre du nœud sera décalé vers la droite d'une quantité PLACE_SUIVANTE[H]-PLACE_CANDIDATE de façon à centrer le nœud par rapport à ses fils.
Pour conserver la linéarité de l'algorithme, cette opération ne peut pas être effectuée directement. Un enregistrement DECALAGE associé à chacun des nœuds doit être géré (un tableau de valeurs indicé sur les nœuds peut aussi être utilisé), dans lequel on retiendra la valeur du décalage à droite sur le sous-arbre du nœud. Un deuxième parcours de l'arbre est donc nécessaire pour placer définitivement tous les nœuds en tenant compte des décalages cumulés. Les champs DECALAGE des sommets d'un même niveau doivent être de valeurs non décroissantes de la gauche vers la droite pour que les sous-arbres leur correspondant ne se chevauchent pas. Un nouveau tableau MODIF donnera au cours du premier parcours la valeur courante de décalage pour chaque niveau afin de tenir compte de cette contrainte.
Algorithme
L'implantation de cet algorithme est réalisé au moyen de deux procédures PLACEMENT_PROVISOIRE et PLACEMENT_DEFINITIF, qui seront appelées successivement sur le nœud racine de l'arbre à dessiner avec des valeurs H et DECALAGE_CUMULE égales à 0.
Procedure PLACEMENT_PROVISOIRE(N : nœud, H : entier)
début
si FILS_GAUCHE(N) ? nil alors
PLACEMENT_PROVISOIRE(FILS_GAUCHE(N),H+1)
PLACEMENT_PROVISOIRE(FILS_DROIT(N),H+1)
fin_si
Y[N] = H
si N est une feuille alors
X[N] = PLACE_SUIVANTE[H]
sinon
PLACE_CANDIDATE = (X[FILS_GAUCHE(N)] + X[FILS_DROIT(N)])/2
MODIF[H] = MAX(MODIF[H],PLACE_SUIVANTE[H]-PLACE_CANDIDATE)
X[N] = PLACE_CANDIDATE + MODIF[H]
fin_si
PLACE_SUIVANTE[H] = X[N] + 2
DECALAGE[N] = MODIF[H)
fin_procedure
Procedure PLACEMENT_DEFINITIF(N : nœud, DECALAGE_CUMULE : entier)
début
X[N] = X[N] + DECALAGE_CUMULE
si FILS_GAUCHE(N) ? nil alors
PLACEMENT_DEFINITIF(FILS_GAUCHE(N),DECALAGE_CUMULE+DECALAGE[N])
PLACEMENT_DEFINITIF(FILS_DROIT(N),DECALAGE_CUMULE+DECALAGE[N])
fin_si
fin_procedure
Les tableaux X, Y, MODIF et DECALAGE sont initialisés à 0, le tableau PLACE_SUIVANTE est initialisé à 1.
L'amélioration apportée par le nouvel algorithme tient au fait que les différents sous-arbres n'ont plus à évoluer dans des zones "distinctes". Ces zones pouvant se recouvrir d'un niveau de l'arbre par rapport à un autre, on peut espérer une meilleure répartition des nœuds dans le plan (Figure 2G).
2.3.3.4 Algorithme de Reingold et Tilford pour le dessin d'arbres binaires
L'algorithme du paragraphe précédent donne de bon résultats dans de nombreux cas. Mais, dans certains exemples, il fournit un dessin inesthétique (Figure 2H).
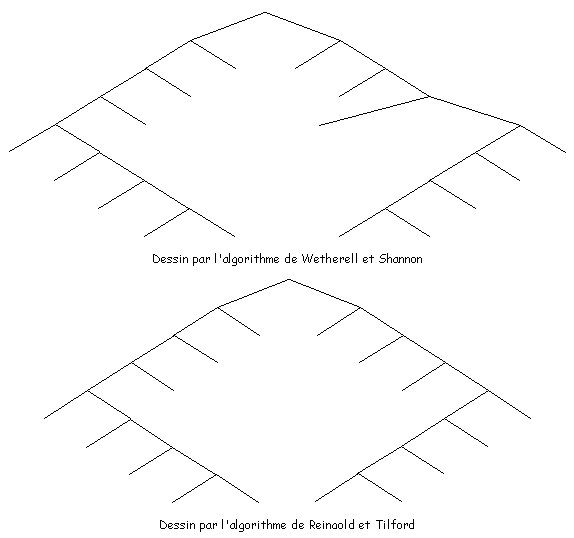
Figure 2H : Dessin par les algorithmes de Wetherell & Shannon et Reingold & Tilford
Le problème provient du choix a priori d'une marge gauche fixe (tableau PLACE_SUIVANTE initialisé à 1). Un tel choix ne respecte pas les symétries éventuelles présentes dans l'arbre à dessiner. On constate que le dessin d'un sous-arbre est influencé par le positionnement a priori des nœuds situés à l'extérieur de ce sous-arbre, ce qui impose de fortes contraintes à résoudre.
Reingold et Tilford en ont déduit la nouvelle contrainte esthétique [RT81] :
Contrainte esthétique 5
Un arbre et son symétrique (par rapport à l'axe des y) doivent être dessinés symétriquement. De plus, un sous-arbre doit être dessiné de la même façon quelle que soit la place où il apparaît dans l'arbre.
Idée de l'algorithme
L'idée de base de l'algorithme de dessin satisfaisant l'esthétique 5 repose sur la construction indépendante des deux sous-arbres fils d'un sommet donné, puis ensuite sur le placement aussi près que possible l'un de l'autre de ces deux sous-arbres. L'algorithme consiste donc dans un parcours de l'arbre en postordre. Lorsque l'on traite le sous-arbre dépendant du nœud n, ses deux sous-arbres fils sont déjà dessinés.
Pour réaliser le placement de ces deux sous-arbres l'un par rapport à l'autre, on les superpose à leur racine puis on les décale de part et d'autre jusqu'à ce qu'ils ne se touchent plus. Cette opération est réalisée niveau après niveau. Etant donnée une séparation minimum SEP_MIN, on commence par décaler symétriquement les deux arbres de manière à séparer leurs racines de SEP_MIN. On passe au niveau suivant : si le fils droit de la racine du sous-arbre gauche et le fils gauche de la racine du sous-arbre droit ne sont pas séparés par au moins SEP_MIN, on décale les deux sous-arbre de la quantité nécessaire à l'obtention de cette séparation (Figure 2I), et ainsi de suite. Une fois les deux sous-arbres séparé par SEP_MIN, le nœud père est alors placé à équidistance de ses deux nœuds fils et les deux sous-arbres fils sont placés définitivement (c'est à dire les coordonnées finales sont affectées aux nœuds) au cours d'un second parcours en préordre où l'on répercute les décalages successifs.
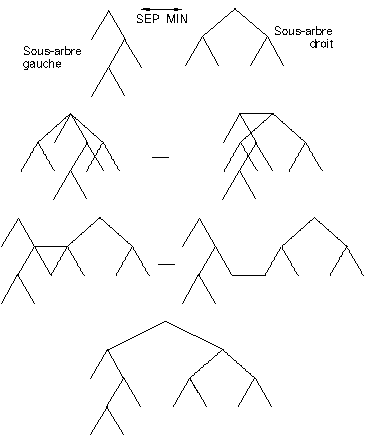
Figure 2I : Etapes du positionnement relatif de deux sous-arbres
Un tel traitement exige de pouvoir parcourir de façon efficace (conservation de la linéarité de l'algorithme) le "contour" droit de l'arbre dépendant du fils gauche et le "contour" gauche de l'arbre dépendant du fils droit, or la seule connaissance des fils droit et gauche de chaque nœud n'est pas suffisante.
Pour résoudre ce problème on va gérer pour chaque sous-arbre deux listes chaînées de nœuds qui vont matérialiser les contours droit et gauche de l'arbre. La gestion de ces listes nécessite suivant les implantations l'adjonction de différents champs à chacun des nœuds de l'arbre et à la racine. Les contours droit et gauche d'un arbre sont établis à partir des contours droit et gauche de ses sous-arbres droit et gauche (Figure 2J).
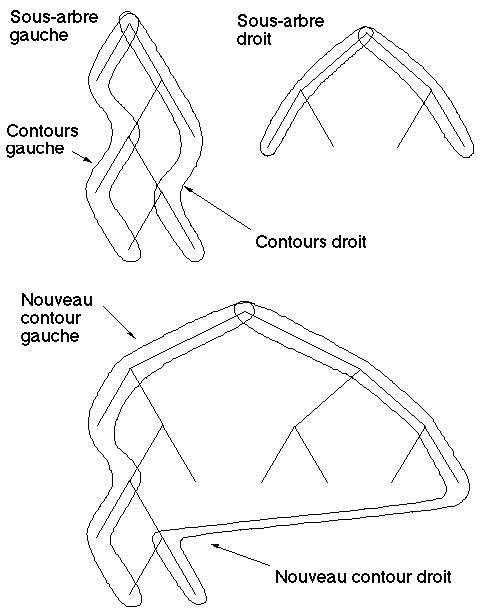
Figure 2J : Calcul des contours droit et gauche d'un arbre à partir de ceux de ses sous-arbres
Algorithme
Deux procédures sont nécessaires à l'implantation. Ces deux algorithmes ne décrivent pas l'extraction des contours droit et gauche. Le dessin d'un arbre est obtenu par appel successif de ces deux procédures sur le nœud racine avec des valeurs de HAUTEUR et de XPOS égales à 0.
Procedure PLACEMENT_RELATIF(N : nœud, HAUTEUR : entier)
debut
si N existe alors
PLACEMENT_RELATIF(FILS_GAUCHE(N),HAUTEUR+1)
PLACEMENT_RELATIF(FILS_DROIT(N),HAUTEUR+1)
Y[N] = HAUTEUR
si N n'est pas une feuille alors
placer les sous-arbres droit et gauche de N
l'un par rapport à l'autre par décalage au
cours du parcours de leurs contours respectifs
gauche et droit
placer N au milieu de ces deux sous-arbres droit et gauche
DECALAGE[N] = distance de N par rapport à ces deux fils
Définir les contours gauche et droit de l'arbre
ainsi construit
fin_si
fin_si
fin_procedure
Procedure PLACEMENT_DEFINITIF(N : nœud, XPOS : entier)
début
si N existe alors
X[N] = XPOS
PLACEMENT_DEFINITIF(FILS_GAUCHE(N),XPOS-DECALAGE[N])
PLACEMENT_DEFINITIF(FILS_DROIT(N),XPOS+DECALAGE[N])
fin_si
fin_procedure
2.4 Conclusion
Un certain nombre d'algorithmes de représentation d'arbres planaires binaires ou quelconques ont été abordés dans les paragraphes précédents. Ces algorithmes permettent d'obtenir des représentations graphiques qui dans la grande majorité des cas seront acceptables et qui sont obtenus dans des temps linéaires du nombre de sommets de l'arbre à représenter.
Dans le chapitre suivant nous verrons d'autres types de modélisations géométriques qui cette fois permettront d'obtenir des représentations planaires d'arbres binaires. Dans la deuxième partie de ce mémoire, une implantation de l'algorithme de Knuth ci-dessus en coordonnées polaires sera mise en œuvre pour obtenir un algorithme automatique de dessin de cartes planaires admettant un arbre binaire donné comme arbre recouvrant. On en déduira alors une nouvelle technique de modélisation et de dessin automatique de bassins montagneux se fondant sur la représentation de leurs bassins fluviaux. On mettra ainsi en évidence un lien entre dessin automatique d'arbres et de cartes planaires.
Ce lien est en fait beaucoup plus profond. Si l'on analyse les algorithmes de dessin d'arbres présentés dans ce chapitre, on constate qu'ils sont caractérisés par une double évolution dans le but de satisfaire des contraintes de plus en plus fines:
1) passage du préordre au postordre dans le traitement des nœuds,
2) abandon de la prise en compte de la marge gauche comme axe de référence initiant le dessin (tableaux "future place libre" du premier algorithme et "place suivante" de l'algorithme de Wetherell et Shannon).
La première évolution s'explique facilement. Affecter les coordonnées en postordre permet de tenir compte de bien plus d'informations : on connaît toutes les coordonnées des nœuds du sous-arbre. On peut donc utiliser cette information dans le but de satisfaire des contraintes géométriques plus fortes. La seconde évolution est également inéluctable. La prise en compte d'une marge gauche a priori, détruit une symétrie éventuelle dans l'arbre.
Ces deux évolutions seront intéressantes à étudier dans le cadre des algorithmes de dessin automatique de cartes planaires. Ont-elles un équivalent? Induisent-elles de nouveaux algorithmes?