Chapitre 3
Synthèse d'images d'arbres
par les matrices de ramification
3 Synthèse d'images d'arbres par les matrices de ramification
3.1 Introduction
La présentation de l'état de l'art en synthèse d'images de paysages a été faite au chapitre 2. Dans ce chapitre, nous proposons une modélisation combinatoire d'un arbre séparant sa forme de son développement. Les travaux présentés dans ce chapitre et les techniques de rendu associées présentées au chapitre 7, ont été publiés dans [Ey86], [VE89a,b], [VJ90] et [AJ90a,b].
Dans le but d'obtenir un meilleur contrôle de la forme finale de l'arbre modélisé, nous insistons d'abord sur la nécessité de définir des paramètres numériques permettant une certaine caractérisation de cette forme, c'est à dire permettant par exemple d'évaluer numériquement des caractéristiques telles que le caractère épineux ou touffu ou encore effilé, bien charpenté ou broussailleux de l'arbre.
La forme de l'arbre est mesurée par l'introduction de la notion de matrice de ramification. Cette matrice est triangulaire stochastique, associée à chaque arbre ou structure ramifiée binaire. Elle dépend seulement de l'arbre topologique sous-jacent. Cette matrice est définie à partir des notions combinatoires d'ordre d'une branche et de biordre d'un nœud interne.
Ces notions apportent une extension de concepts introduits par les hydrogéologistes Horton [Ho45] et Strahler [St52]. L'utilisation de l'analyse d'Horton-Strahler pour la synthèse d'images d'arbres a été suggérée mais non développée dans [EF86]. Ici nous développons cette approche en introduisant le concept de matrice de ramification permettant de séparer la forme de l'arbre de son histoire, et en montrant que beaucoup d'aspects visuels liés à l'aspect de l'arbre combinatoire, sont présents dans la matrice associée. Récemment, cette notion a été utilisée pour l'étude physique de structures ramifiées fractales, Vannimenus, Viennot [Va87], [VV89].
Notre méthode consiste à choisir une matrice de ramification et ensuite à effectuer la génération aléatoire d'un arbre combinatoire binaire dont la matrice de ramification est identique (ou très proche) de la matrice choisie. Enfin, la géométrie est définie. L'idée principale est de contrôler l'épaisseur et la longueur des arêtes et des angles d'embranchement par des lois linéaires, polynomiales ou exponentielles des ordres et biordres.
La méthode est simple et rapide, tout en préservant une grande variété de formes possibles. Bien que ce modèle soit différent des modèles botaniques, un rendu réaliste peut être obtenu. Dans ce but, nous introduirons au chapitre 7 un algorithme rapide de dessin de feuilles. L'aspect réaliste est également développé dans [VE89a].
3.2 Les nombres de Strahler et les matrices de ramification
3.2.1 Arbre topologique, arbre géométrique et arbre botanique
Afin d’éviter toute confusion entre arbre botanique, topologique ou géométrique nous rappelons les quelques notions suivantes (voir par exemple Knuth [Kn73]).
Un arbre binaire topologique ou mathématique est défini par un ensemble de nœuds (ou sommets) joints par des arêtes. Il existe deux types de nœuds, les nœuds internes (ou nœuds de branchement) et les nœuds externes (ou nœuds terminaux ou feuilles). Chaque nœud interne est caractérisé par le fait qu’il possède deux fils : un fils droit et un fils gauche. En revanche, les nœuds externes n’ont pas de fils. Un nœud interne est appelé le "père de ses fils". Une arête joint chaque nœud père à chacun de ses deux fils. Le nœud racine de l’arbre est le seul nœud qui ne possède pas de père. Il est intéressant d’ajouter à partir de la racine de l'arbre une arête virtuelle appelée arête racine pour matérialiser un tronc (Figure 3A). La taille d'un arbre binaire est par définition égale à son nombre de nœuds internes.
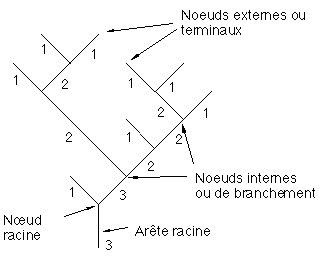
Figure 3A : Un arbre
Un arbre topologique peut être associé à toute structure ramifiée naturelle. Il sera selon les cas binaire, ternaire ou d'arité quelconque. Nous considérerons que cet arbre est binaire dans le cas des arbres botaniques (ce qui représente une large majorité des cas pour les espèces feuillues). En botanique chaque arête de l’arbre binaire topologique est appelée segment de branche. Nous verrons plus loin que cette définition est différente de celle que nous utiliserons.
L'arbre géométrique est indissociable de l'arbre topologique qui a permis de le calculer. Il regroupe toutes les informations à caractère géométrique. Celles-ci seront calculées au moyen de modèles géométriques appliqués à l'arbre topologique. Dans sa forme minimale l'arbre géométrique comprend seulement les positions de tous les nœuds de l’arbre, celles-ci pouvant être données en deux ou en trois dimensions. Cette seule information est suffisante pour obtenir un aperçu de la forme de l'arbre (représentation en fil de fer). Pour pouvoir effectuer des dessins réalistes, d'autres informations doivent être apportées. Elles n'entrent toutefois pas toutes dans le cadre d'un modèle géométrique. On citera par exemple l'épaisseur des branches, la méthode de modélisation de ces branches en 2D ou en 3D (prismes, cylindres, branches droites ou courbes), le type de texture à appliquer si elle existe, l’utilisation de feuilles, ... Le modèle géométrique minimal de représentation réaliste inclura la position de tous les nœuds ainsi que l'épaisseur de toutes les arêtes.
3.2.2 Ordres et segments
Les sommets d’un arbre binaire quelconque sont étiquetés au moyen de la fonction récursive suivante (FILS_DROIT et FILS_GAUCHE sont deux fonctions qui admettent comme paramètre un nœud interne et qui rendent en résultat respectivement son nœud fils droit et son nœud fils gauche) :
Fonction ETIQUETTE(NŒUD : nœud) : entier
STD,STG : entier
début
si NŒUD est un nœud terminal alors
ETIQUETTE = 1
sinon
STD = ETIQUETTE(FILS_DROIT(NŒUD))
STG = ETIQUETTE(FILS_GAUCHE(NŒUD))
si STD = STG alors
ETIQUETTE = STD+1
sinon
ETIQUETTE = MAX(STD,STG)
fin_si
fin_si
fin_fonction
On voit donc que les nœuds terminaux sont tous étiquetés 1, les étiquettes des nœuds d'un arbre quelconque vont en décroissant de la racine où ils sont maximum, vers les feuilles.
On appelle étiquette etiquette(a) d’une arête a allant d’un sommet n à l’un de ses fils f, l’étiquette du nœud f. L’étiquette d’un nœud (respectivement arête) est appelée ordre de ce nœud (respectivement arête) (Figure 3A). Cette méthodologie d'étiquetage des arêtes et des nœuds d’un arbre binaire a été développée par les hydrogéologistes Horton [Ho45] (sous une forme légèrement différente) et Strahler [St52] pour l'étude morphologique des bassins fluviaux. Ils ont établi que ces ordres tels qu'ils sont calculés, sont assez représentatifs de l'importance relative des différentes composantes d'un fleuve (débit, largeur, ...).
L’ordre de l’arête racine (l’ordre du sommet racine) est appelé nombre de Strahler de l’arbre. Un segment d’ordre k est une séquence maximale d’arêtes consécutives d’ordre k. Notons enfin que le concept d’ordre est différent de celui utilisé en botanique ([RE88] ou [PL88]), où l’ordre n’est pas définissable pour un arbre binaire figé dans le temps mais dépend de l’histoire de l’arbre.
3.2.3 L’analyse d’Horton-Strahler en hydrogéologie et autres sciences
Beaucoup d’études ont été entreprises en hydrogéologie pour examiner la morphologie des réseaux fluviaux. En particulier, chez Horton et Strahler ([Ho45], [St52]) la notion de rapport de bifurcation ßk d’ordre k a été élaborée. Un réseau fluvial est supposé sans île ni point de jonction triple ou multiple (cette hypothèse simplificatrice représente en fait une très large majorité des cas). Ces conditions étant vérifiées, l’arbre topologique sous-jacent est un arbre binaire. Si bk est le nombre de segments d’ordre k contenus dans l'arbre topologique alors ßk est le rapport bk-1/bk. Par exemple l’arbre de la figure 3A possède des rapports de bifurcation ß2 = 8/2 = 4 et ß3 = 2/1 = 2.
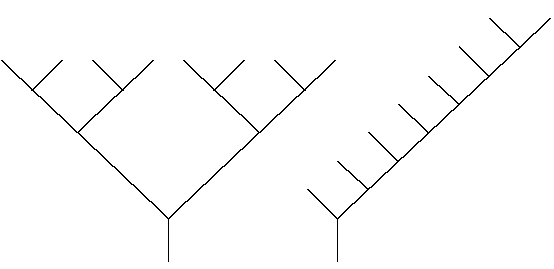
Figures 3B et 3C : Arbre parfait et arbre très fin
Ces rapports donnent une information très partielle sur la forme de l’arbre binaire topologique: les arbres des figures 3B et 3C montrent des cas extrêmes. L’arbre parfait de profondeur 3 (chaque nœud terminal a la même profondeur) (Figure 3B) a tous ses segments réduits à des arêtes uniques : chaque rapport de bifurcation est égal à 2 (valeur minimale possible quelque soit l'arbre). Pour l’arbre très fin (Figure 3C), il n'y a qu'un seul segment d’ordre 2, et chaque arête terminale est un segment d’ordre 1. Le rapport de bifurcation d’ordre 2 est égal au nombre de nœuds terminaux, il n'est donc pas limité car l'arbre peut être de profondeur tendant vers l'infini.
Les géologistes ont établi que les rapports de bifurcation sont habituellement compris entre 3 et 5 dans la nature. Nous définissons un arbre binaire aléatoire comme étant un arbre binaire choisi aléatoirement avec équi-probabilité parmi les Cn = (2n)! / n! / (n+1)! arbres binaires à n nœuds internes. Il est connu que tous les rapports de bifurcation d'un arbre binaire aléatoire approchent 4 quand le nombre de nœuds devient grand (cf Meier et Moon [MM80]). Des études similaires ont été effectuées pour d'autres structures ramifiées, comme en botanique par MacMahon [Ma75] ou en anatomie par Woldenberg [Wo70] et neurophysiologie par Percheron [Pe82]. Prud'homme et Vigneaux [PV70] ont prouvé qu'il existe une certaine corrélation entre l'analyse de Horton-Strahler et la structure tectonique du sous-sol. Cette analyse a aussi été faite sur les réseaux de vallées des montagnes sous-marines (Naudin et Prud'homme [NP71]). Curieusement, le nombre de Strahler d'un arbre est aussi apparu en informatique pour évaluer le nombre minimum de registres nécessaires au calcul d'une expression arithmétique, (Flajolet, Raoult et Vuillemin [FR79], Kemp [Ke79]), et en biologie moléculaire pour l'étude de la "complexité" de la forme et pour le calcul de l'énergie des structures secondaires d'acides nucléiques (ARN) (Vauchaussade de Chaumont et Viennot [VV85]).
3.2.4 Un modèle de topologie des arbres : les matrices de ramification
3.2.4.1 Biordre d’un nœud interne
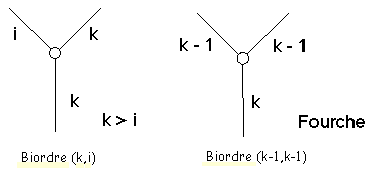
Figure 3D : Biordres
Considérons dans un arbre topologique binaire quelconque un nœud interne n d’ordre k ayant deux nœuds fils d’ordres i et j avec j=i. Si j>i alors j = k et le biordre du nœud n est définit comme la paire (k,i). Si j = i (et donc = k-1), le biordre du nœud n est (k-1,k-1) (Figure 3D).
3.2.4.2 Matrice de ramification extraite d’un arbre binaire
Pour un arbre binaire T on définit :
- pour k = 2, ak est le nombre de nœuds internes d’ordre k,
- pour 1 = i < k, bk,i est le nombre de nœuds de biordre (k,i),
- pour k = 2, bk,k est le nombre de nœuds de biordre (k-1,k-1),
- pour 1 = i = k, pk,i = bk,j
/ ak.Le nombre pk,i est la probabilité pour un nœud interne d’ordre k d’avoir le biordre (k,i) ou (k-1,k-1) si k = i. La matrice de ramification Ram(T) de l’arbre binaire T avec le nombre de Strahler s est la matrice stochastique (la somme des composantes de chaque ligne est égale à 1) de dimension (s-1) x s dont les composantes (k,i) (1=i=k=s,2=k=s) sont les pk,i.
![]()
Table 3A : Matrice de ramification de l'arbre de la figure 3A
La table 3A donne la matrice de ramification de l’arbre binaire de la figure 3A.
3.2.4.3 Extraction de la matrice de ramification associée à une classe d'arbres
Supposons que l'on dispose d'une méthode de génération d'arborescences binaires topologiques. Le but est de définir, si c'est possible, la matrice de ramification associée à cette classe d'arborescences.
Une méthode simple consiste à calculer la matrice moyenne d'un ensemble de matrices extraites à partir d'arbres de cette classe de même taille T et de même nombre de Strahler S. On obtient ainsi une matrice moyenne représentative des arbres de taille T et de nombre de Strahler S appartenant à cette classe.
On peut ensuite vouloir mettre en évidence un phénomène de convergence de la matrice moyenne calculée vers une matrice limite quand la taille des arbres et, par voie de conséquence, le nombre de Strahler de l'arbre deviennent très grands.
Un problème se pose sur les dernières lignes des matrices moyennes calculées, car pour deux arbres de taille T1 et T2 différentes mais possédant deux nombres de Strahler identiques (et donc une matrice de ramification possédant le même nombre de lignes), la répartition des probabilités sur les dernières lignes des matrices peut être différente (voir les trois dernières lignes des tables 3B et 3C). En effet, la différence de taille entre deux arbres d'une même classe ayant des nombres de Strahler identiques s'explique souvent par des différences de longueurs sur les segments d'ordres égaux (ou très peu inférieurs) à l'ordre de l'arbre, ce qui se traduit par des valeurs différentes sur les dernières lignes de leurs matrices de ramification extraites (voir également le paragraphe 3.5.6 qui décrit l'influence de la matrice de ramification sur la taille de l'arbre généré).
Une autre raison est que les biordres associés à ces lignes sont peu nombreux dans l'arbre et conduisent donc à des calculs statistiquement peu significatifs.
On ne peut donc prendre en compte que les lignes qui restent quasiment identiques quelle que soit la taille de l'arbre. Une conséquence importante est que des arbres de très grande taille (plusieurs dizaines de milliers de nœuds internes, voire plus) auront généralement à être analysés statistiquement pour obtenir une réponse fiable et précise sur un nombre important de lignes de la matrice limite extraite.

Table 3B : Matrice statistique extraite sur les arbres binaires aléatoires croissants de taille 10000 et de nombre de Strahler 10

Table 3C : Matrice statistique extraite sur les arbres binaires aléatoires croissants de taille 32000 et de nombre de Strahler 10
3.2.4.4 Exemples de matrices de ramification
3.2.4.4.1 Arbre parfait
La matrice de ramification calculée pour les arbres binaires parfaits (arbres dont tous les nœuds terminaux sont de la même profondeur, Photographie 3A) est donnée à la table 3D. Toute arête d'ordre k doit se ramifier en deux arêtes d'ordres k-1. On a donc obligatoirement une diagonale composée uniquement de 1 et les coefficients de la partie inférieure de la matrice égaux à 0.
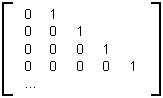
Table 3D : Matrice de ramification des arbres parfaits.

Photographie 3A : Arbre binaire parfait (taille égale à 511, nombre de Strahler égal à 10)
3.2.4.4.2 Arbre binaire aléatoire
On appelle arbre binaire aléatoire de taille n un arbre binaire de n nœuds internes tiré au hasard parmi les Cn =
Comme il a été précisé au paragraphe 3.2.4.3, les deux dernières lignes de la table 3E ne sont pas représentatives de la convergence vers une matrice limite. Toutefois les six premières lignes mettent bien en évidence l'évolution des lignes ce qui permet d'établir la table 3F, matrice limite pour les arbres binaires aléatoires.

Photographie 3B : Arbre binaire aléatoire (taille égale à 500, nombre de Strahler égal à 5)
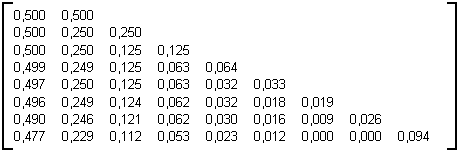
Table 3E : Matrice statistique des arbres binaires aléatoires de taille 10000
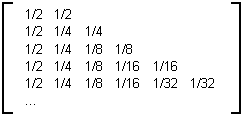
Table 3F : Matrice limite des arbres binaires aléatoires
On remarque sur cette matrice une première ligne de valeur assez importante égale à 0.5, ainsi que des valeurs sur la diagonale qui s'affaiblissent d'un facteur deux à partir d'une valeur de 0.5 à chaque fois que l'on descend une ligne à l'intérieur de la matrice.
3.2.4.4.3 Arbre binaire aléatoire croissant
Un arbre binaire aléatoire croissant de taille n peut être généré au moyen de l'algorithme suivant :
générer un arbre T1 n'ayant qu'un nœud interne
Pour i de 2 à n
choisir avec équiprobabilité
un nœud terminal de l'arbre Ti-1
créer un nœud fils droit et un nœud fils gauche
au nœud choisi de manière à générer l'arbre Ti
Fin_pour
En cours d'exécution de cet algorithme, chaque arbre intermédiaire Tn a n nœuds internes mais n'est pas un arbre binaire aléatoire au sens de la définition du paragraphe précédent. Si les nœuds internes sont numérotés de 1 à n dans l'ordre de leurs créations, les nœuds fils ont toujours une étiquette supérieure à celle de leur père. Remarquons qu'un arbre binaire aléatoire croissant n'est autre qu'un arbre binaire de recherche associé à une permutation aléatoire.
Un exemple d'arbre binaire aléatoire croissant est donné à la photographie 3C (voir aussi les planches 2B, 2C, 7, …).
Si la taille des arbres créés varie (augmente), la convergence vers une matrice limite apparaît. Le calcul de la matrice moyenne table 3G d'un grand nombre de matrices de ramifications d'arbres binaires aléatoires croissants de grande taille (1000 arbres de 30000 nœuds internes) nous permet d'établir que cette matrice limite est proche de celle donnée à la table 3G'.
Sur la table 3G' ne sont indiquées que les lignes certaines, dans la pratique on extrait trois lignes supplémentaires pour les arbres de taille 30000 (table 3G) mais les variations fonctions de la taille de l'arbre généré sont très importantes sur ces lignes.
On constate sur cette matrice que les valeurs sur les diagonales se stabilisent très vite. Ainsi, par extrapolation à partir de la table 3G', il serait possible d'établir les lignes suivantes de cette matrice en introduisant des lignes supplémentaires identiques à la dernière avec un décalage à chaque niveau.

Photographie 3C : Arbre binaire aléatoire croissant (taille égale à 500, nombre de Strahler égal à 7)
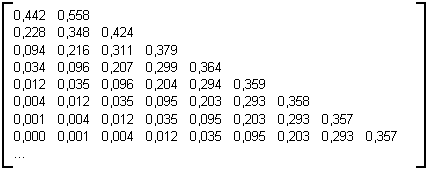
Table 3G' : Matrice limite des arbres binaires aléatoires croissants
Sur cette matrice on constate la présence de valeurs assez fortes sur la diagonale, tandis que les valeurs vont en décroissant depuis la diagonale en descendant les colonnes et en parcourant les lignes de droite à gauche.

Table 3G : Matrice moyenne des arbres binaires aléatoires croissants de taille 30000
3.2.4.4.4 Tries

Photographie 3D : Trie généré avec s = 12 et card(
w) = 1000Une des structures les plus connues pour stocker un ensemble de mots binaires est celle de "Trie" (Photographie 3D). On rappelle ci-après l'algorithme de construction des Tries proposé dans Flajolet, Regnier et Sotteau [FR85].
Bs = {0,1}s étant l'ensemble des mots binaires de taille s, on associe à tout sous-ensemble
w de Bs un arbre binaire noté Trie (w) selon l'algorithme :- Si card(
w) = 0, alors Trie(w) est l'arbre vide.- Si card(
w) = 1, alors Trie(w) est formé d'une unique feuille étiquetée w.- Si card(
w) = 2, alors Trie(w) est constitué d'une racine dont les sous-arbres gauche et droit sont respectivement les Tries associés aux sous-ensembles w0 et w1 de Bs-1 définis par : wi = {v Œ Bs-1 / iv Œ w}.On contrôle la taille des Tries générés en jouant sur les deux paramètres numériques s et card(
w) (= 2s), il n'est pas possible de fixer a priori cette taille. Plus card(w) est grand avec une valeur s fixe, plus la taille de l'arbre créé est grande (tableau 3H).s \ card( w) |
25 |
50 |
100 |
200 |
400 |
800 |
1600 |
3200 |
6400 |
9 |
32,6 |
63,9 |
121 |
223.6 |
406.8 |
x |
x |
x |
x |
10 |
33,5 |
66,5 |
129.1 |
243 |
448.6 |
814.8 |
x |
x |
x |
11 |
34,15 |
68,4 |
134.7 |
257.7 |
487 |
896.8 |
1630.1 |
x |
x |
12 |
34,49 |
69,5 |
137.8 |
267.9 |
516.9 |
973.5 |
1794.1 |
3261.5 |
x |
13 |
34,72 |
70,4 |
140.1 |
275.8 |
537.9 |
1033.3 |
1948.9 |
3593.6 |
6522.6 |
14 |
34,80 |
70,9 |
141.7 |
280.1 |
552.5 |
1077.1 |
2068.3 |
3902.1 |
7183.3 |
Tableau 3H : Taille moyenne d'un Trie en fonction de s et de card(
w)En effectuant un calcul de moyenne sur 2500 tries avec s = 13 et card(
w) = 8000, on trouve la matrice de ramification de la table 3I. Il est à signaler que tous les arbres obtenus ont eu pour nombre de Strahler la valeur 12. Quels que soient s et card(w), la dispersion des nombres de Strahler est toujours très faible, ce qui se traduit bien dans la forme très équilibrée des arbres.
Table 3I : Matrice de ramification statistique des tries avec s = 13 et card(
w) = 8000
Table 3J : Matrice de ramification statistique des tries avec s = 18 et card(
w) = 500On remarque que cette matrice est concentrée sur la diagonale et sa sous-diagonale, ce qui, du point de vue de la répartition des probabilités sur les lignes, la place entre la matrice des arbres parfaits et celle des arbres binaires aléatoires. La forme de la matrice varie en fonction des valeurs card(
w) et s. Si s augmente avec une même valeur de card(w), ou si card(w) diminue avec une même valeur de s, les sous-diagonales suivantes (la 3ème et éventuellement la 4ème) peuvent adopter des valeurs qui ne seront pas toutes nulles (comparer les tables 3I et 3J). Même avec des valeurs de s très grande et de card(w) très petite, toutes les sous-diagonales à partir de la 5ème si elles existent sont nulles.3.2.4.4.5 Le modèle d'Eden
Le modèle d'Eden de génération d'une structure arborescente est défini de la manière suivante [VV89] :
A partir d'un point de diffusion unique (la racine de l'arbre binaire topologique en construction) composé d'une seule particule, une nouvelle particule vient s'agglutiner à chaque étape de la génération de telle manière que celle-ci (la particule) ne touche en tout et pour tout qu'une seule autre particule (Photographie 3E). L'emplacement d'implantation est choisi au hasard parmi toutes les positions ayant une seule particule adjacente.

Photographie 3E : Représentation écran d’un arbre généré par le modèle d’Eden 2D.

Photographie 3F : Arbre de la photographie 3E dessiné avec notre modèle géométrique
Les hypothèses utilisées pour une génération en 2D sont les suivantes :
- Chacune des particules est considérée comme étant carrée, il y a donc quatre positions adjacentes à toute particule (en haut, en bas, à droite et à gauche).
- Pour pouvoir générer un arbre topologique, l'adjonction d'une particule à une place quelconque ne devra pas créer de cycle.
- Pour obtenir un arbre binaire mathématique, l'adjonction d'une particule ne devra pas créer de nœud d'arité trois (une particule possède une autre particule dans toutes ses positions adjacentes).
Nombre de particules |
Taille |
100 |
25 |
200 |
50.4 |
500 |
125.9 |
1000 |
251.9 |
2000 |
502 |
5000 |
1262 |
10000 |
2497 |
20000 |
4981 |
Tableau 3K : Taille des arbres générés par modèle d'Eden 2D
Il est bien entendu possible de travailler en dimension quelconque, les particules seront alors des hypercubes. Le nombre de positions adjacentes est égal à 2*n, où n est le nombre de dimensions de l'espace de travail. On doit toujours ne pas créer de cycle ou de nœud d'arité 3 ou plus.
La taille de l'arbre topologique obtenu dépend du nombre de particules utilisées comme le montre le tableau 3K. Dans le modèle d'Eden 2D, on note un facteur approximatif de 4 entre le nombre de particules générées et la taille de l'arbre obtenu.
Le calcul de la matrice de ramification moyenne pour un grand nombre d’arbres générés au moyen du modèle d'Eden en 2D (Photographie 3F) donne la matrice 3L (arbres de 10000 particules et donc de d'environ 2500 nœuds internes, 82% d'arbres de nombre de Strahler 7 et 18% de nombre de Strahler 8).
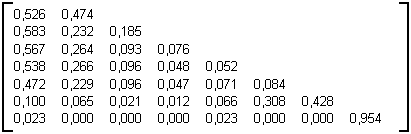
Table 3L : Matrice statistiques des arbres générés par modèle d'Eden 2D avec 10000 particules
On constate immédiatement que cette matrice de ramification est très semblable à celle des arbres binaires aléatoires (Paragraphe 3.2.4.4.2) à l'exception des deux dernières lignes qui ne sont toutefois pas représentatives. Cette méthode physique de génération d’arbres binaires rend compte d’un phénomène topologique quasiment aléatoire.
3.2.4.5 Auto-similarité
Un certain nombre des matrices de ramification présentées aux paragraphes précédents présentent la particularité d'être auto-similaires. Par cela, nous entendons que les variations des probabilités des biordre sur chacune des lignes sont du même type. En d'autres termes, si nous visualisons cette variation par une courbe extrapolant les points (j,pk,j) pour 1=j=k, toutes les courbes associées à chaque ligne sont analogues.
Lorsque cette propriété est vérifiée, nous dirons que l'arbre binaire est (statistiquement) auto-similaire (pour la matrice de ramification). Notons que cette notion est différente, quoique liée, de celle introduite par Mandelbrot [Ma82]. La matrice de ramification d'un tel arbre auto-similaire peut être visualisée par une courbe. Ces courbes sont dessinées sur la figure 3E pour les types d'arbres qui ont été introduits dans les paragraphes précédents.
3.2.4.6 Matrices de ramification en physique
Des travaux ont récemment été entrepris en physique sur des structures ramifiées arborescentes rencontrées dans la nature. Citons par exemple les éclairs électriques, Niemeyer, Pietronero, Wiesman [NP84], la "digitation visqueuse", Nittmann, Daccord, Stanley [ND85], VanDamme et al. [VO86], les précipités de métal électrolytique, Sawada, Dougherty, Gollub [SD86] ou les bien connus "Diffusion Aggregation Process (DLA)" de Witten et Sanders [WS81] et Ball [Ba86].
Ces modèles sont considérés ou approximés par des structures ramifiées fractales. Leur aspect visuel est usuellement mesuré par les physiciens avec un nombre unique : la dimension fractale (voir Mandelbrot [Ma82]).
Récemment, ces structures ramifiées ont été étudiées par application du modèle des matrices de ramification, Vannimenus, Viennot [VV89], Vannimenus [Va87]. Le Modèle d'Eden arborescent, la "digitation visqueuse" et le "2D DLA model" ont aussi été étudiés. Les matrices de ramification sont encore auto-similaires. Les courbes correspondantes sont proches de celle associée aux arbres binaires aléatoires (Figure 3E). La construction des arbres binaires aléatoires croissants est analogue à celle du modèle d'Eden en dimension infinie (Evident). La grande différence entre les deux courbes de la figure 3E (modèle d'Eden 2D et arbres binaires aléatoires croissants) montre la forte influence de la contrainte de planarité.
3.3 Génération d'un arbre topologique au moyen d'une matrice de ramification
Soient une matrice R, stochastique triangulaire de dimension (s-1) x s, ainsi qu’un nombre entier S (S = s). L’algorithme proposé ci-dessous permet la génération d’un arbre T qui aura pour nombre de Strahler S et dont la matrice de ramification extraite sera statistiquement voisine de celle obtenue en considérant les lignes 2 à S de R.
La génération débute à partir d’un arbre T1 réduit à une seule arête (l’arête racine de l’arbre généré) étiquetée S. Une séquence Tn d’arbres binaires étiquetés va être construite. L’arbre Tn+1 de taille n+1 est obtenu à partir de l'arbre Tn en choisissant une arête terminale de Tn étiquetée k (k ? 1) et en créant sur cette arête deux arêtes filles étiquetées respectivement k et i (i < k) ou k-1 et k-1. Le choix (k,i) ou (k-1,k-1) est effectué par sélection aléatoire en accord avec la distribution des probabilités des biordres donnée sur la kième
ligne de la matrice R. L’algorithme prend fin quand toutes les arêtes terminales sont étiquetées 1.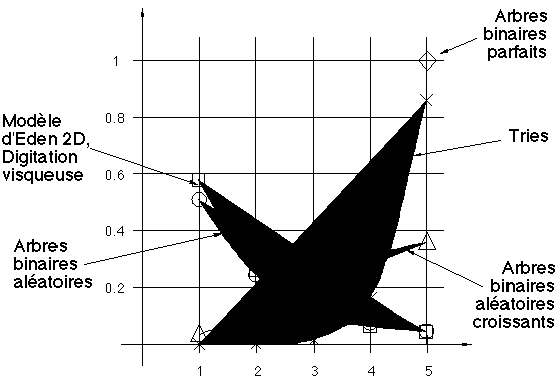
Figure 3E : Matrices de ramifications auto-similaires
Cet algorithme peut être implanté sous la forme de la fonction récursive GENERATION suivante qui rend un nœud correspondant à la racine de l'arbre généré (ST est le nombre de Strahler de l'arbre binaire à générer, MAT est la matrice de ramification devant guider la génération) :
Fonction GENERATION(ST : Entier,
MAT : Matrice_ramification) : nœud ;
I,J : Entier
N : nœud
Début
Créer un nœud N ;
Si ST ? 1 alors
Choisir un biordre (I,J) sur la ligne ST
de la matrice Mat en accord avec la distribution
des probabilités ;
Le fils droit de N <- GENERATION(I,MAT) ;
Le fils gauche de N <- GENERATION(J,MAT) ;
Sinon
n est terminal et n'a ni fils droit ni fils gauche
Fin_si
GENERATION <- N ;
Fin_fonction
L’expérimentation montre que, comme il est attendu, la matrice de ramification extraite à partir de l’arbre final T de nombre de Strahler S est proche de la matrice initiale R, en particulier en ce qui concerne les premières lignes (celles correspondant aux petits ordres) et quand la taille de l’arbre est suffisamment grande (plus de quelques centaines de nœuds). Le contrôle de la taille finale n de l’arbre s’opère en choisissant son nombre de Strahler S, il n'est pas possible de fixer n a priori (Figure 3F).
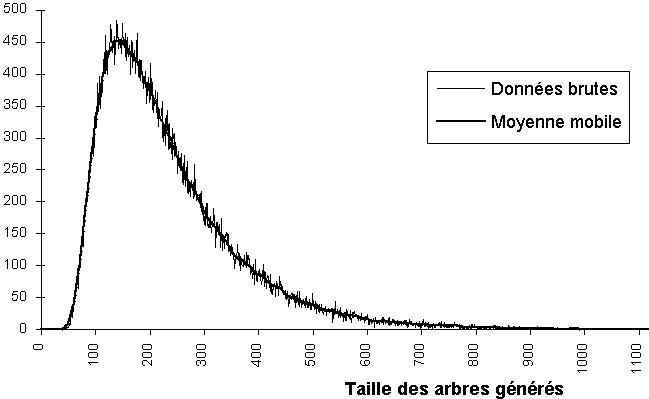
Figure 3F : Variation de la taille d’un arbre de nombre de Strahler 7 généré à partir de la table 3G
Les photographies jointes (Planches 1, 2, …) représentent des arbres générés au moyen de matrices de ramification, de nombre de Strahler compris entre 5 et 10, et des tailles obtenues variant de quelques centaines à quelques milliers de nœuds.
Orientation de la structure
Dans l’algorithme précédent, pour le cas de l’évolution d'un nœud en un biordre (k,i) avec i < k, nous n’avons pas précisé quelle arête (la droite ou la gauche) reçoit l'étiquette k (cette arête sera l'arête principale du branchement). Ce choix permet d’influer sur la forme de l’arbre.
Une première possibilité est d’effectuer ce choix aléatoirement (équiprobabilité pour chaque côté). Une seconde option est d’alterner les arêtes principales tantôt à droite, tantôt à gauche sur chaque segment de l’arbre. Il est aussi possible de fixer le choix de telle manière que l’arête principale soit toujours du même côté. Une dernière option consiste à choisir l’orientation de la branche principale de telle manière qu'elle tende à se rapprocher d'une direction prédéterminée. Il est ainsi possible de simuler un tropisme qui pourra matérialiser par exemple l'action du vent dans une direction donnée ou du soleil (phototropisme) (voir planche 7B). Ce choix ne peut être fait avant que les coordonnées des nœuds pour une modélisation 2D ou 3D n’aient été calculées. Pour cette dernière option, il y a donc obligation d'effectuer le calcul simultané de la topologie et de la géométrie.
3.4 Les modèles géométriques
3.4.1 Introduction
Il est maintenant nécessaire de définir les modèles géométriques employés car si le modèle topologique laisse supposer des possibilités importantes dans le paramètrage des formes pouvant être générées, il est quasiment impossible de bien se représenter ces formes sans une représentation graphique. L'étude du modèle topologique peut très bien s’effectuer au moyen d'algorithmes de plongement géométrique travaillant en deux dimensions, mais un rendu vraiment réaliste (ce qui est notre but final, ne l'oublions pas) ne pourra être obtenu qu'en modélisant la géométrie et en dessinant en trois dimensions. La limitation au 2D permet d'envisager un calcul de la géométrie ainsi qu'un dessin relativement rapide (Chapitre 7, annexe 1). Tandis que le passage au 3D réaliste, s'il ne change rien du point de vue topologique, va entraîner un surcoût temporel important pour la modélisation géométrique, ainsi que pour la phase de dessin (Chapitre 7, annexe 1).
3.4.2 Le modèle 2D
Une géométrie élémentaire est plaquée sur l’arbre topologique en déterminant les positions dans le plan de chacun des nœuds, ainsi qu’en attribuant une épaisseur à chacune des arêtes.
Dans la pratique, le modèle géométrique nous donne (Figure 3G) :
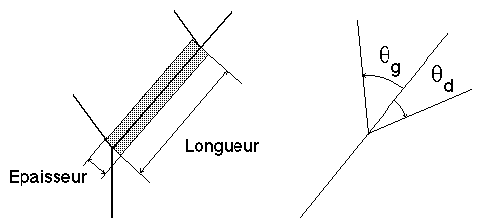
Figure 3G : Epaisseur, longueur, 2 angles de branchement
- Pour chaque arête a, une épaisseur E(a) et une longueur L(a).
- Pour chaque nœud interne n, deux angles
qg(n) et qd(n), le premier en valeur positive, le second en valeur négative, définissant la déviation des arêtes filles gauche et droite associées à n par rapport à leur arête mère.L’idée directrice de notre démarche est de faire dépendre les lois de longueur et d'épaisseur d'une arête uniquement de son ordre k, et les deux angles de déviation
qg et qd relatifs à un nœud interne uniquement du biordre de ce nœud.Pour ces quatre paramètres nous avons choisi des lois en correspondance avec les effets esthétiques que l’on est en droit d’attendre de l’image de l’arbre vis à vis de la réalité. Pour une étude plus précise voir Honda [Hon71], Leopold [Le71], Mendes-France [Me81], Stevens [St74],.... Pour les arbres, comme pour beaucoup d’autres structures ramifiées naturelles, l’épaisseur des arêtes décroît assez régulièrement de la racine aux nœuds terminaux. En général il en est de même pour la longueur des arêtes. Il est naturel de choisir les lois d’épaisseur et de longueur comme des fonctions croissantes E(k) et L(k) de l’ordre k de l’arête concernée.

Loi quadratique Loi linéaire Loi constante
Photographie 3G : Influence du type de lois de longueur sur l'aspect de l'arbre

Loi exponentielle Loi constante
Photographies 3H : Influence du type de lois d'épaisseur sur l'aspect de l'arbre
Sur les photographies 3G et 3H les lois sont constante, linéaire ou quadratique pour L(k) et polynomiale ou exponentielle pour E(k) :
L(k) = cl1 + cl2 * k + cl3 * k2
E(k) = ce * k
a ou E(k) = ce * ßkavec cl1, cl2, cl3, ce,
a et ß des constantes numériques.Des lois présentant des effets esthétiques analogues à la nature ont été choisies pour les angles
qg et qd. Ces lois vérifient la propriété suivante :Propriété (1)
A un embranchement donné, une branche fille subit une déviation d'autant plus petite que cette branche est importante.
Cette règle peut être modulée en faisant une distinction dans les lois appliquées entre la branche fille principale et la branche fille secondaire (Constantes cp et cs ci-dessous).
Dans notre modèle l’importance d’une branche est mesurée par son ordre. Plus il est grand, plus la branche est importante. Les lois suivantes ont donc été utilisées (Figure 3H ) :
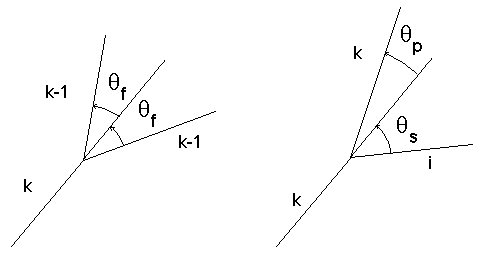
Figure 3H : Angles
qf,qp et qs- Pour un embranchement de biordre (k-1, k-1) que nous appellerons fourche, les deux branches filles sont d’égale importance, leurs déviations sont égales en valeur absolue et
qg = -qd = qf, qf est une constante réelle positive.- Pour un nœud avec un biordre (k,i) i<k, les angles de déviation respectifs
qp et qs de la branche principale et de la branche secondaire vis à vis de leur branche mère sont donnés par :q
p(k,i) =où cp et cs sont des constantes réelles positives. Dans le cas où la branche fille gauche est la branche principale du biordre alors
qg = qp, sinon qg = qs. Si la branche fille droite est la branche principale alors qd = -qp, sinon qd = -qs.De bons résultats visuels sont obtenus avec cs et
qf égaux à 30° et cp égal à 10°. Bien sûr il est possible d’adopter toute autre paramètrisation en fonction de l’image voulue (Photographie 3I). Il est important de signaler que ces formules vérifient obligatoirement la propriété (1), toutefois pour certaines valeurs des coefficients cp et cs et du biordre (i,k) la déviation de la branche principale peut être plus importante que celle de l'autre branche (en valeur absolue). Si l'on veut obtenir une stricte observation de (1) et une déviation toujours moins importante pour la branche principale que pour la branche secondaire, on peut choisir :q
p(k,i) =où c est un coefficient réel positif.
Ces lois sont plus simples dans leur formulation, mais elles permettent des variations géométriques moins importantes. L'angle entre les deux branches filles d'un nœud interne est constant égal au coefficient c quel que soit le nœud considéré.

q
p = 6, qs = 10 et qf = 10 qp = 6, qs = 20 et qf = 20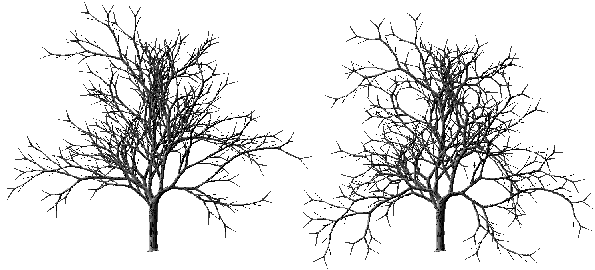
qp = 10, qs = 30 et qf = 30 qp = 15, qs = 40 et qf = 40
Photographie 3I : Influence des coefficients angulaires sur l'aspect de l'arbre
Pour le dessin 2D, ces formules sont suffisantes pour définir totalement un modèle minimum de géométrie de l’arbre. Les coordonnées de chaque sommet peuvent être calculées récursivement en utilisant les longueurs et les paramètres d’angle. L’épaisseur n’entrera réellement en compte qu'au cours de la phase de dessin.
Le modèle géométrique 2D n'interdit pas aux différentes arêtes de l'arbre de se recouper, ce qui peut, même seulement en 2D, simuler avantageusement un dessin trois dimensions (Planches 1 et 2). On notera aussi qu'une bonne qualité de représentation n'est pas tributaire d'un choix plus ou moins aléatoire de ces angles. Des valeurs déterministes peuvent même être d'un grand avantage dans la cas où l'on désire analyser la forme d'un arbre, ou si l'on veut modéliser l'évolution comme on le verra au chapitre suivant.
3.4.3 Le modèle 3D
Le modèle de calcul des angles d'orientation dans le cas d'un modèle en deux dimensions est bien adapté à l'étude visuelle des propriétés caractéristiques d'arbres topologiques binaires. L'obtention d'un dessin réaliste est toutefois tributaire de la définition d'un modèle géométrique 3D. Un angle de phyllotaxie (angle de déviation en projection dans le plan orthogonal à l'axe de la branche mère) doit être défini à chaque embranchement pour l'orientation de chacune des branches filles. Il apparaît possible de modifier notre modèle 2D pour en conserver les principales caractéristiques géométriques (propriété (1)).
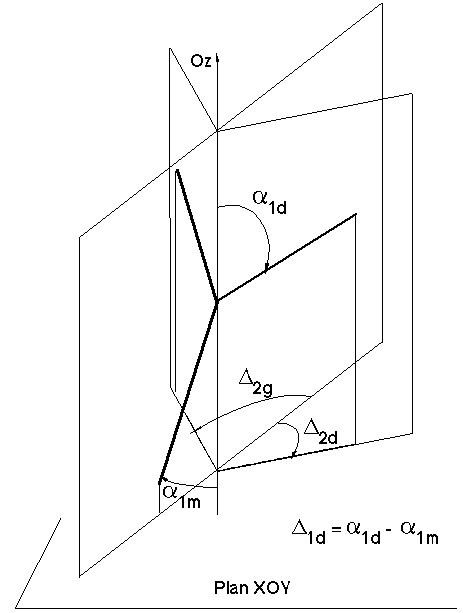
Figure 3I : Définition des angles d'orientation 3D
Par rapport au modèle 2D, la modélisation géométrique en 3D nécessite l'utilisation de deux angles au lieu d'un seul pour définir la déviation que subit une arête fille par rapport à son arête mère. Le modèle 3D comprend les formules de calcul permettant d'évaluer ces deux angles de déviation à chacun des embranchements.
- Les angles D1d et D1g des filles droite et gauche représenteront les angles de déviation par rapport à la mère dans le plan de la verticale. Plus précisément, pour la branche fille droite par exemple, si a1m (resp a1d) est l'angle de la mère (resp. fille droite) avec la verticale, alors D1d = a1d - a1m.
- Les angles D2d et D2g des filles droite et gauche donneront les angles de déviation en projection dans le plan xOy (Figure 3I).
Le calcul des épaisseurs et des longueurs des branches s'effectuera d'une manière identique au modèle 2D. Les formules de calcul des deux angles de déviation ainsi que de l'épaisseur et de la grosseur d'une arête permettent de définir la position dans l'espace de n'importe quelle branche fille à partir de la position de sa branche mère.
3.4.3.1 Angle de déviation par rapport à la verticale
L'angle ?1 nous donne une déviation par rapport à la branche mère par rapport à la verticale. Intuitivement cette déviation suit les mêmes lois que celles adoptées pour les déviations des branches dans le modèle 2D, qui nous permettaient d'obtenir de bons résultats visuels. C'est à dire qu'une branche fille sera d'autant moins déviée qu'elle est importante. Les formules données pour les déviations du modèle 2D restent donc valables pour l'angle de déviation ?1 du modèle 3D. A partir de la branche racine verticale, on définit récursivement les déviations ?1 des branches filles vis à vis de leurs branches mères.
Les formules utilisées sont fonction des biordres (les indices p, s et f signifiant "principale", "secondaire" et "fourche", voir paragraphe 3.4.2):
D1p(k,i) =ou bien, comme il a été signalé précédemment :
D1p(k,i) =3.4.3.2 Angle de déviation en projection dans le plan xOy
En revanche, pour l'angle de déviation en projection sur le plan xOy, les lois de calcul du modèle 2D ne peuvent pas être appliquées directement. En effet quelques constatations simples les réfutent (on parle ici d'angles en projection dans le plan xOy):
- Il est possible de trouver dans un arbre botanique des branches filles droites et gauches adoptant des directions diamétralement opposées comme il est possible de trouver des branches filles droites et gauches suivant des directions quasiment identiques (Figure 3J).
- L'importance respective des branches filles ne nous apporte pas toujours d'informations pertinentes sur leurs déviations respectives.
Un paramètre important pour le calcul de l'angle de déviation en projection sur le plan xOy d'une branche fille apparaît être l'angle a1m par rapport à la verticale adoptée par sa branche mère. En effet, plus la branche mère est verticale plus l'orientation des branches filles dans le plan xOy semble être prise au hasard (Figure 3J). Il est relativement logique de penser que si une branche mère est quasiment verticale (son angle dans le plan xOy n'a alors guère d'influence sur son orientation globale dans l'espace), il sera difficile de calculer l'angle de déviation ?2 pour une de ses branches filles. On en prendra pour exemple toutes les espèces d'arbres qui possèdent un axe de croissance vertical (croissance apicale orthotropique) (sapin, épicéa, peuplier, ...), où sur la branche principale quasi verticale (le tronc) viennent se fixer toutes les autres qui partent dans toutes les directions (la répartition de toutes ces branches est globalement équilibrée pour que l'arbre ne tombe pas sur le coté). En revanche, si la branche mère est quasi-horizontale les branches filles suivent la direction initiée par la branche mère dans le plan xOy (Figure 3J). On considérera alors que, dans ce cas là, la déviation suit le même type de lois que celles du modèle géométrique 2D.
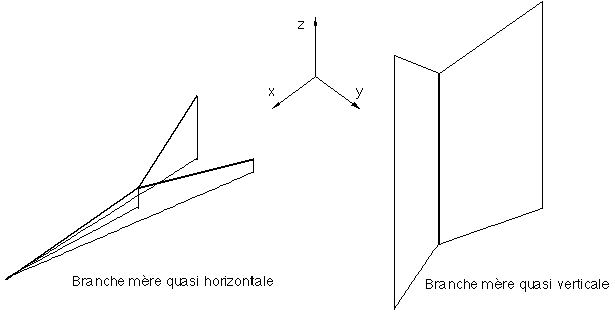
Figure 3J: angles de déviations dans le plan xOy.
A partir de ces constatations, il est possible de modifier les lois de calcul des déviations pour les réadapter au calcul des angles
D2. Ces angles sont toujours calculés avec les mêmes lois fonction de la valeur du biordre du nœud considéré, mais ils sont entachés d'une incertitude qui est d'autant plus importante que la branche mère est verticale. Cette incertitude est donc maximale (en fait l'angle D2 est totalement pris au hasard) si l'angle de la branche mère par rapport à la verticale est égal à 0 ou 180°, elle est minimale (égale à 0) si cet angle est égal à 90°. On a donc : D2p(k,i) =La fonction INCERTITUDE permet de calculer un angle matérialisant l'incertitude entachant la valeur de
D2. Cette fonction possède comme paramètre l'angle a1m par rapport à la verticale de la branche mère de l'arête dont on cherche la déviation en projection dans le plan xOy. Cette fonction pourra être par exemple :Incertitude (a1m) = ![]() * RAND()
* RAND()
où RAND() est une fonction qui rend un entier positif pris au hasard entre 0 et 359.

Géométrie 2D Géométrie 3D
Photographie 3J : Une même structure topologique avec les modèles géométriques 2D et 3D
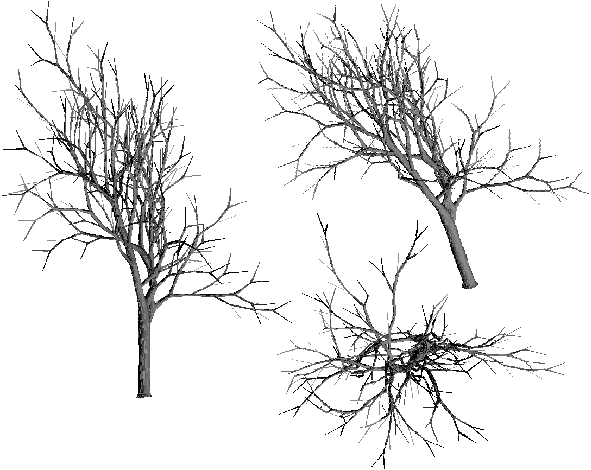
Photographie 3K : Un arbre sous différents points de vue
3.4.4 Conclusion
L'utilisation d'une géométrie 3D n'apporte pas d'avantage déterminant pour l'étude des aspects purement topologiques concernant les arbres, elle serait même éventuellement pénalisante car les branches se recoupent beaucoup plus et les angles d'orientation sont beaucoup moins réguliers qu'avec une géométrie 2D (Photographie 3J). En revanche, en utilisant une géométrie 3D il devient possible d'obtenir un aperçu d'un même arbre de différents points de vue (Photographie 3K, planches 6, 8 et 10), ce qui peut être intéressant dans le cadre d'un dessin réaliste.3.5 Relation entre forme et taille d'un arbre et la matrice ramification
3.5.1 Préliminaires
La matrice de ramification est liée à l’arbre topologique sous-jacent à un arbre géométrique binaire. La "forme" de cet arbre topologique est manifestement un concept purement abstrait, l’étude des relations entre les matrices de ramification et la forme de l’arbre ne pouvant être effectuée qu’à partir d'une représentation géométrique. Cependant quelle que soit la géométrie ajoutée sur les arbres des figures 3B et 3C, celui de gauche restera toujours bien équilibré et celui de droite aura toujours l'aspect d'une liane. Il semble donc possible de parler de "forme" de l'arbre topologique, indépendamment de toute géométrie. A cette fin, les images présentées dans la suite seront toutes réalisées avec les mêmes paramètres géométriques, en géométrie 2D avec rendu 3D. En se détachant ainsi au maximum de l'influence de la géométrie, on pourra mettre en évidence plus facilement les relations entre matrice de ramification et forme de l'arbre topologique.
3.5.2 Exemples caractéristiques
Deux matrices typiques conduisant à des résultats visuels manifestement très différents sont celles données aux tables 3M et 3N, c’est à dire les matrices de ramification des arbres binaires aléatoires et binaires aléatoires croissants.

Table 3M : Matrice limite des arbres binaires aléatoires

Table 3N : Matrice limite des arbres binaires aléatoires croissants
Dans le premier cas (Table 3M), nous obtenons des arbres assez aérés avec une forme élancée, chevelue où l'on note la présence de quelques longs segments sur lesquels beaucoup d’épines (nœuds de biordre (k,1)) sont implantées (dans la réalité ces épines sont trop petites pour être bien vues sur la photographie 3L). Ces arbres ressemblent beaucoup à des lierres ou aux essences que l'on peut rencontrer dans les sous-bois et qui sont caractérisées par le fait qu'elles poussent tout droit vers le ciel sans générer beaucoup de feuilles du fait du manque de soleil. Les épines et les petits rameaux respectivement associés aux biordres (k,1) et (k,2) concentrent 75% des probabilités d'apparition des biordres, ce qui est important. La caractéristique fondamentale de ce type d'arbres est donc l'apparition de très longs segments quels que soient leurs ordres, segments sur lesquels se greffent une multitude de petits arbres (d'ordres très petits) (Planche 1A).
La seconde matrice (Table 3N) donne naissance à une classe d’arbres qui contiennent beaucoup plus de branches importantes et qui sont beaucoup mieux équilibrés (Photographie 3L), ils ressemblent d'ailleurs beaucoup plus aux arbres tels qu'on se les représente intuitivement. Dans cette matrice 60 à 70% des probabilités des biordres sont concentrées sur les deux dernières valeurs de chaque ligne (diagonale et première sous-diagonale). L’aspect "bien équilibré" est dû aux fortes probabilités des biordres (k-1,k-1) donnant ainsi naissance à un grand nombre de fourches comparativement au nombre total de nœuds internes (sans toutefois arriver à un rapport égal à 1 qui donne un aspect totalement bien équilibré dans le cas des arbres binaires parfaits). Très peu d’épines ou de petits rameaux apparaissent sur les branches d’ordres élevés. Les segments sont relativement courts.

Photographie 3L : Influence de la matrice de ramification sur la forme de l'arbre
3.5.3 Influence des coefficients sur la diagonale
Les valeurs présentes sur la diagonale d'une matrice de ramification ont
une influence directe sur la longueur moyenne des segments de l'arbre généré au moyen
de cette matrice. En effet, ces coefficients représentent la probabilité, pour un
nœud d'ordre k quelconque d'évoluer en deux nœuds d'ordres k-1, ce qui
représente la probabilité qu'un segment se finisse à chaque fois qu'on avance d'un
nœud en le parcourant. La longueur moyenne d'un segment d'ordre k sera donc obtenue
en calculant ![]() (paragraphe 3.5.6). Plus les valeurs sur la diagonale sont
petites, plus les segments créés seront longs, et plus l'arbre semblera élancé et
tourmenté (s'éloignant de la forme caractéristique de l'arbre binaire parfait). Pour
les arbres binaires aléatoires croissants, la longueur moyenne des segments tend vers une
limite voisine de 2,78 pour les grands ordres, pourtant l'arbre reste encore assez bien
équilibré (Photographies 3C et 3L, planches). En revanche pour la matrice des arbres
binaires aléatoires, la longueur moyenne de ces segments d'ordre k est égale à 2(k-1).
Elle croit donc très vite quand k augmente. Ces arbres présentent des segments qui
deviennent rapidement très longs, la forme générale de l'arbre est assez
caractéristique (Photographies 3B et 3L, planches).
(paragraphe 3.5.6). Plus les valeurs sur la diagonale sont
petites, plus les segments créés seront longs, et plus l'arbre semblera élancé et
tourmenté (s'éloignant de la forme caractéristique de l'arbre binaire parfait). Pour
les arbres binaires aléatoires croissants, la longueur moyenne des segments tend vers une
limite voisine de 2,78 pour les grands ordres, pourtant l'arbre reste encore assez bien
équilibré (Photographies 3C et 3L, planches). En revanche pour la matrice des arbres
binaires aléatoires, la longueur moyenne de ces segments d'ordre k est égale à 2(k-1).
Elle croit donc très vite quand k augmente. Ces arbres présentent des segments qui
deviennent rapidement très longs, la forme générale de l'arbre est assez
caractéristique (Photographies 3B et 3L, planches).
Contrainte par segment
Lors de la création d'un arbre au moyen une matrice de ramification, pour
obtenir des arbres plus réguliers, on peut imposer une contrainte supplémentaire
appelée "contrainte par segment" qui implique que la longueur de tous
les segments d'ordre k soit égale à leur longueur moyenne c'est à dire : ![]() .
.

Photographie 3M : Arbres de même matrice de ramification avec et sans contrainte par segments.
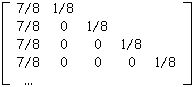
Table 3O : Matrice à forte première ligne
La photographie 3M montre les différences pouvant apparaître entre un arbre subissant une contrainte par segment lors de sa création et un arbre n'en subissant pas, la matrice de ramification utilisée au cours de la génération étant identique pour les deux arbres. La matrice employée est celle donnée à la table 3O. Avec cette matrice la longueur moyenne des segments est égale à 8. On constate que l'arbre avec contrainte par segment est beaucoup plus régulier que l'arbre sans contrainte. On tiendra compte du fait que sur l'arbre gauche, chaque branche entre deux fourches est en fait un segment de longueur 8, les épines dues aux biordres (k,1) inférieures à la taille du pixel, n'apparaissant pas. Un autre exemple est présenté à la planche 1A.
3.5.4 Influence de la répartition des coefficients sur les lignes
La répartition en valeur des coefficients sur chacune des lignes influence aussi la forme de l'arbre généré (à valeurs identiques sur la diagonale bien entendu). Plus les probabilités situées immédiatement sous la diagonale sont grandes plus les branches s'implantant sur les segments auront un ordre important. Deux conséquences sont directement issues de cette constatation.
- Il est évident que plus un arbre a un nombre de Strahler important, plus sa taille sera statistiquement grande. Avec des sous-diagonales fortes, pour un même segment d'ordre k, les ordres des branches implantées seront donc grands (ordres k-1, k-2, ...), et les tailles de ces sous-arbres seront grandes. Donc plus les coefficients sous les diagonales seront grands, plus la taille des arbres générés sera grande.
- D'un point de vue visuel, la génération d'arbres plus ou moins touffus est ainsi possible. En effet, en augmentant l'importance des sous-diagonales immédiates, on réduit le nombre d'épines ou d'arbres d'ordre 2, 3,... pouvant être générés sur chaque segment et donc l'arbre semblera d'autant plus touffu (Planche 1B).
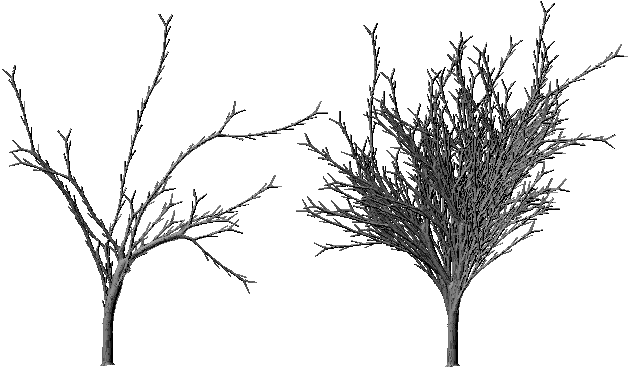
Photographie 3N: Arbres générés avec des matrices à sous-diagonales faibles et fortes.
La photographie 3N montre la comparaison entre deux arbres de même nombre de Strahler générés avec les matrices table 3P et table 3Q. Celles-ci présentent les mêmes valeurs sur la diagonale, on a simplement choisi de grandes valeurs pour les biordres (k,k-2) dans la table 3P tandis que ces valeurs apparaissent sur les biordres (k,k-1) dans la table 3Q.
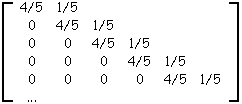
Table 3P : Matrice à 1
ère sous-diagonale nulle et 2ème sous-diagonale forte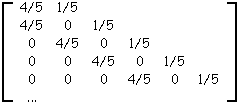
Table 3Q : Matrice à 1
ère sous-diagonale forte et 2ème sous-diagonale nulleOn voit que l'arbre avec sous-diagonale forte est beaucoup plus touffu que l'autre. L'arbre de droite possède en fait 1283 nœuds internes tandis que celui de gauche n'en possède que 160.
3.5.5 Mélange de lignes de matrices différentes
La paramètrisation des coefficients sur les lignes des matrices permet d'obtenir la génération d'arbres possédant des caractéristiques précises (voir paragraphes précédents). Une autre possibilité permettant de faire varier les formes obtenues consiste à mélanger les lignes de diverses matrices pour générer des arbres qui posséderont les caractéristiques de ces matrices sur leurs branches. Par exemple, on peut construire une matrice de ramification qui regroupera les lignes 2 à 4 de la matrice des arbres parfaits, puis les lignes 5 et 6 de la matrice des arbres aléatoires, et enfi
n les lignes 7 à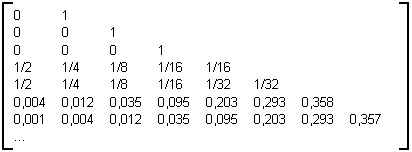
Table 3R : Matrice obtenue par mélange de lignes
Un arbre généré au moyen de cette matrice de ramification possédera (Photographie 3O) des segments d'ordres 2 à 4 identiques aux segments 2 à 4 des arbres parfaits, des segments d'ordres 5 et 6 de même forme que les segments d'ordres 5 et 6 des arbres binaires aléatoires (de longs segments) et enfin des segments d'ordres 7 à
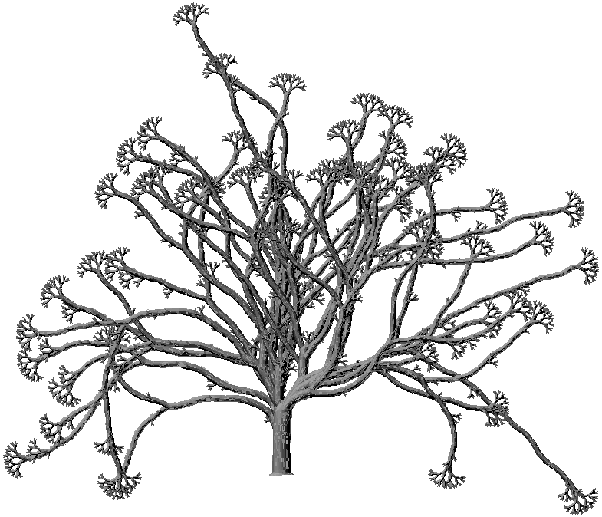
Photographie 3O : Influence de la matrice de ramification sur la forme de l'arbre : mélange de lignes de matrice d'arbres parfaits, d'arbres aléatoires et d'arbres aléatoires croissants
3.5.6 Taille moyenne d'un arbre généré par une matrice de ramification
Un problème théorique intéressant consiste à évaluer a priori la taille moyenne d'un arbre généré par une matrice de ramification. Cette information peut être utilisée à titre indicatif avant le lancement de l'algorithme de génération.
Soit une matrice de ramification M (triangulaire inférieure) de dimension D dont les lignes sont numérotées de 2 à D. Cette matrice contient les probabilités d'apparition Pj,i
des biordres (j,i) lors de la génération (Pj,j est associée aux biordres (j-1,j-1)). Soit S (S £ D) le nombre de Strahler de l'arbre binaire T que l'on désire générer au moyen de la matrice M. Le calcul de la taille de T consiste à trouver les nombres moyens nj,i ( 1 £ i < j) de nœuds internes de biordres (j,i), nj,j de nœuds internes de biordres (j-1,j-1) (de façon à respecter les notations de la définition de la matrice de ramification), générés par utilisation de cette matrice, et par somme de ces nombres moyens, le nombre moyen de nœuds internes contenus dans l'arbre.Longueur moyenne d'un segment d'ordre j
La longueur moyenne d'un segment d'ordre j est notée Lj. C'est la moyenne de la variable
lj qui à un segment d'ordre j associe sa longueur. lj prend ses valeurs dans N*. lj sera égal à n avec la probabilité (1 - Pj,j)n-1 * Pj,j. En effet, pour qu'un segment d'ordre j soit de longueur n, il faut :1) que les n-1 premiers biordres générés à partir de l'origine de ce segment soient du type (j,i) avec i < j (ils sont générés avec la probabilité qj = 1 - Pj,j)
2) que le dernier sommet soit fourche (j-1,j-1), c'est à dire généré avec la probabilité Pj,j.
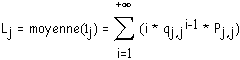
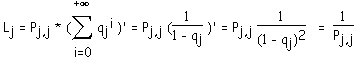 (1)
(1)
Nombre moyen de nœuds de biordre (j,i) sur un segment d'ordre j (1
£ i < j)Sur un segment d'ordre j (de longueur moyenne Lj), les nombres moyens de nœuds de biordres (j,i) (1
£ i < j) sont distribués proportionnellement aux probabilités Pj,i :![]() (2)
(2)
Cette formule reste vraie avec i = j :
hj,j = 1Nombre moyen de segments d'ordre j
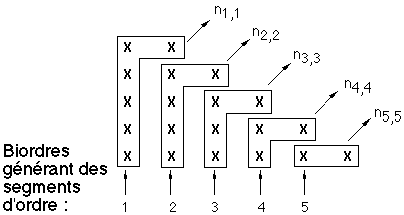
Figure 3K : Calcul des nombres de segments d'ordre j
Le nombre moyen de segments d'ordre j est d'une part égal au nombre nj,j de biordres (j-1,j-1) (qui sont les biordres terminaux de ces segments) et est d'autre part égal à la somme des nombres d'apparition des biordres (k,i) tels que j = k ou j = i, biordres qui donnent naissance aux segments d'ordre j (On comptera double un biordre (j,j) donnant naissance à deux segments d'ordre j). On comptabilise ainsi le nombre de nœuds d'ordre j qui sont les premiers nœuds d'un segment d'ordre j. Les nombres recherchés sont donc nj+1,j+1 correspondant au biordre (j,j) (ce nombre est compté deux fois car le biordre contient deux j et donne naissance à deux segments d'ordre j), nj+1,j, nj+2,j, ..., nS,j (voir figure 3K).
Cette double façon d'exprimer le nombre moyen de segments d'ordre j conduit à la formule :
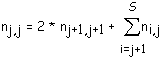 (3)
(3)
La valeur nS,S n'est pas calculable par cette formule. Elle est égale à 1 car nS,S représente le nombre de segments d'ordre S.
Nombre moyen de nœuds de biordre (j,i) (1
£ i < j)Le nombre moyen de nœuds de biordres (j,i) (1
£ i < j) est alors le nombre moyen de nœuds de biordre (j,i) par segment d'ordre j multiplié par le nombre moyen de segment d'ordre j :![]() (4)
(4)
Nombre total moyen de nœuds internes
Le nombre moyen de nœuds internes de T est égal à la somme des nombres de biordres calculés par utilisation des formules ci-dessus jusqu'à la ligne S :
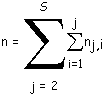 (5)
(5)
L'évaluation des nombres moyens de biordres nj,i est effectuée ligne après ligne, de la ligne S à la ligne 2 de manière à n'utiliser dans la formule (3) que des valeurs déjà déterminées. En effet, la combinaison de (3) et (4) nous permet d'établir :
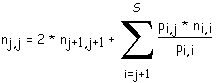
nj,j dépend donc de nj+1,j+1, nj+2,j+2, ..., nS,S. Toutes ces valeurs doivent être connues avant le calcul de nj,j.
Dans la pratique, on constate une grande variabilité de la taille des arbres générés (voir figure 3E) qui peut fluctuer de manière importante autour de la valeur théorique, mais la valeur moyenne est bonne (voir tableau 3S). Ce phénomène s'explique par les tirages stochastiques au cours de l'algorithme de génération.
Matrice |
Nombre de Strahler |
Nombre d'arbres générés |
Temps de calcul |
Taille moyenne calculée |
Taille moyenne observée |
Table 3D |
6 |
40000 |
2 heures 30 |
235,29 |
235,14 |
Table 3D |
7 |
100000 |
20 heures |
716,76 |
716,38 |
Table 3C Bis |
6 |
43000 |
8 heures |
682,82 |
684,24 |
Table 3M |
4 |
30000 |
2 heures |
215 |
215,2 |
Tableau 3S : Comparaison entre tailles calculées et tailles observées
A titre indicatif, les arbres présentés dans les exemples de cette thèse possèdent des nombres de Strahler variant de 5 à 10 suivant le type de matrice de ramification, le nombre de nœuds obtenus varie de quelques centaines à quelques milliers.
Remarque
Si l'on a extrait la matrice de ramification d'un arbre donné quelconque, les formules précédentes donnent exactement (les calculs sont à résultats entiers) les nombres nj,i de nœuds internes de biordre (j,i) de l'arbre de départ. Il est donc possible de retrouver à partir de cette matrice de ramification la taille exacte de l'arbre pour lequel elle a été déterminée.
Exemple

Soit la matrice de ramification suivante extraite d'un arbre quelconque, nous allons retrouver de nombre de nœuds de l'arbre initial à partir des probabilités d'apparition calculées des biordres contenus dans la matrice. Par application de (3) et (4) en remontant les lignes à partir de nS,S = 1, on reconstruit la suite suivante des matrices dont la dernière donne les nombres de nœuds internes répartis par biordres :
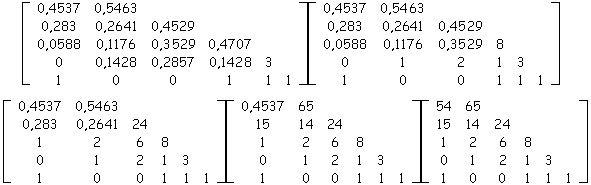
Par simple somme des nombres de biordres on retrouve le nombre de nœuds internes contenus dans l'arbre qui était 200.
3.6 Conclusion
La topologie est essentielle dans la méthode présentée qui autorise l'analyse d'une structure ramifiée indépendamment de son histoire. Ceci conduit aux matrices de ramification qui sont l' expression des caractéristiques principales de la forme d'une structure ramifiée. Comme nous l'avons vu, ces matrices permettent un fort contrôle de la forme finale et sont un outil pour la synthèse d'images de structures arborescentes présentant de telles caractéristiques. A partir d'une méthode de génération d'une classe d'arbres, il est possible d'extraire de façon simple la matrice de ramification représentant cette classe d'arbres. Cette association entre l'analyse de l'image et la synthèse d'image est l'un des points intéressants de cette méthode.
L'association d'une géométrie dépendant seulement des paramètres combinatoires ordre et biordre, avec un algorithme rapide de dessin de feuilles (cf chapitre 7 et annexe 1) est un bon compromis entre la vitesse et le rendu final, tout en conservant une grande diversité de formes possibles. Une telle méthode simple et rapide est d'un intérêt pratique pour l'implémentation d'un environnement interactif de génération et d'animation d'arbres dans des domaines variés (botanique, arts graphiques, architecture, …). On en donnera un exemple en synthèse d'images de paysages au chapitre 8 : Des milliers d'arbres synthétisés par les techniques décrites dans ce chapitre seront implantés dans un bassin montagneux de façon à générer des images réalistes de montagnes. L'efficacité de ces méthodes permet alors (cf chapitre 8 pour les détails) la création de plusieurs centaines d'images d'un tel bassin montagneux muni de milliers d'arbres pour la réalisation d'un survol animé du paysage (voir logiciel "Survol" en annexe d'animation sur Macintosh). Ce résultat est intéressant puisque réalisé sur un micro-ordinateur IBM PS/2 8580, cf chapitre 8 et annexe 1 pour les détails.
L'intérêt scientifique se rencontre alors dans l'analyse et la synthèse de structures ramifiées qui ne sont pas nécessairement botaniques, par exemple en physique (éclairs électriques, "digitation visqueuse", DLA, …) et en biologie moléculaire (structures secondaires d'ARN). En particulier, le modèle des matrices de ramification a été appliqué récemment en physique aux structures fractales ramifiées [Va87] [VV89].
Cette méthode des matrices de ramification, si elle permet la génération d'arbres topologiques présentant des caractéristiques de forme précises en fonction d'un petit nombre de valeurs numériques, présente cependant des arbres figés à un instant donné dans le temps sans possibilité d'évolution. Le but du chapitre 4 suivant est de présenter une nouvelle technique combinatoire, dans le même esprit que la précédente mais permettant de simuler l'évolution des végétaux modélisés.