Chapitre 4 : Les matrices d'évolution : une méthode de modélisation de la croissance de structures ramifiées binaires

Chapitre 4

Les matrices d'évolution:

une méthode de modélisation de la croissance

de structures ramifiées binaires

4 Les matrices d'évolution : une méthode de modélisation de la croissance de structures ramifiées binaires

4.1 Introduction

La génération d'arbres binaires par la méthode des matrices de ramification est, nous l'avons vu au chapitre précédent, bien adaptée à l'obtention d'arbres binaires de caractéristiques de forme précises. Toutefois, cette méthode ne permet pas de simuler simplement un phénomène de croissance. Le but de ce chapitre est de montrer le moyen de générer des arbres avec les mêmes facilités qu'au moyen les matrices de ramification (caractérisation facile de la forme de l'arbre généré en fonction d'un petit nombre de coefficients), mais en permettant de simuler un phénomène de croissance de la structure.

Associant une technique combinatoire de modélisation de l'arbre topologique et la croissance de cet arbre, la méthode présentée ici, dite "méthode par matrice d'évolution", permet la représentation d'un arbre à différentes étapes de sa croissance. Cette matrice d'évolution est stochastique, triangulaire supérieure, infinie dans les deux directions. Elle permet de quantifier la forme et l'aspect visuel de l'arbre, mais pilote de plus la croissance de l'arbre génération après génération, permettant de contrôler l'aspect visuel de cet arbre à chacune de ces générations. On verra ainsi sur les photographies ci-jointes un arbre être bien équilibré pendant les premières étapes de sa croissance, puis devenir chevelu avec de longs segments dans les étapes suivantes de son évolution et enfin achever sa croissance par l'apparition de petits arbres parfaits. Cette notion de matrice d'évolution permet de piloter la croissance des branches de l'arbre binaire topologique.

Dans cette méthode l'arbre topologique sous-jacent joue un rôle essentiel, en particulier pour quantifier la forme de l'arbre finalement représenté. Les liens entre matrice d'évolution et matrice de ramification sont présentés en fin du chapitre.

4.2 Matrice d'évolution : Outil pour la synthèse et l'analyse de la croissance d'une structure arborescente

4.2.1 Paramètres combinatoires associés à la synthèse de la croissance d'une structure arborescente

La croissance d'une arborescence topologique binaire va être modélisée comme une suite de n générations successives. La génération i permet de passer d'un arbre d'âge i à un arbre d'âge i+1 (arbre âgé de i années par exemple). Nous allons modéliser ici un phénomène de croissance par les bords. C'est à dire qu'au cours de la génération i certaines arêtes terminales de l'arbre seront actives et évolueront en segments (voir définition plus loin). L'algorithme 1 ci-dessous, décrivant cette génération courante I, utilise les paramètres combinatoires suivants:

4.2.1.1 Ordre d'évolution d'un noeud

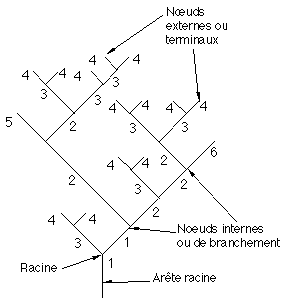
Image001.gif (3406 octets)

Figure 4A : Exemple de répartition d'ordres dans un arbre

On associe à chaque noeud s de l'arbre un ordre Ordre(s) dit ordre d'évolution représentant le numéro de la génération à laquelle ce noeud se ramifiera en deux noeuds fils. Cet ordre est ainsi un entier, l'ordre d'évolution de la racine étant donné égal à 1.

On impose de plus aux ordres d'évolution associés aux noeuds de satisfaire à la règle suivante : Les deux noeuds fils d'un noeud étiqueté i sont étiquetés i et j > i, ou i+1 tous les deux (cas d'une fourche), (Figure 4A).

On définit l'ordre Ordre(e) d'une arête e allant d'un sommet v à l'un de ses fils s comme étant l'étiquette Ordre(s) de s.

4.2.1.1.1 Remarques

La règle d'attribution des ordres d'évolution implique bien évidemment que l'ordre d'évolution d'un nœud fils est supérieur ou égal à l'ordre de son père. Plus une arête quelconque aura un ordre d'évolution de petite valeur plus cette arête sera importante dans l'arbre et donc plus proche de la racine.

L'égalité des ordres d'évolution de plusieurs nœuds successifs sur un chemin allant de la racine à une feuille de l'arbre traduit l'apparition de ces nœuds en cascade au cours d'une même génération lors de la création d'un segment. On appellera segment d'ordre d'évolution k une telle séquence maximale d'arêtes consécutives d'ordre k créées au cours de la génération k.

Notons enfin que le concept d'ordre d'évolution est totalement différent de celui usuellement introduit en botanique ([RE88] ou [PL88]), où l'ordre n'est pas défini pour un arbre binaire mais dépend de l'histoire du développement de l'arbre.

4.2.1.1.2 Ordre d'évolution et ordre de Strahler

La notion d'ordre d'évolution ainsi définie est à l'opposée de celle introduite en hydrogéologie par Horton et par Strahler ([Ho45], [St52]). Les ordres d'évolution croissent de la valeur 1, pour le tronc, aux ordres d'évolution des feuilles qui sont maximum dans l'arbre (il n'y a aucun nœud interne possédant un ordre supérieur à l'ordre minimum de toutes les feuilles). A l'opposée, les ordres de Strahler pour ce même arbre décroîtront du nombre de Strahler du tronc (du nœud racine), qui est maximum dans l'arbre, à la valeur 1 attribuée à toutes les feuilles. La notion de segment d'ordre d'évolution k est en revanche tout à fait similaire à la notion de segment définie pour les ordres de Strahler.

Nous verrons que les deux notions d'ordre sont très liées bien qu'ayant des possibilités différentes. Le paragraphe 4.7 décrira plus précisément les relations numériques existant entre les ordres de Strahler et les ordres d'évolution pour un même arbre.

4.2.1.2 Biordre d'évolution

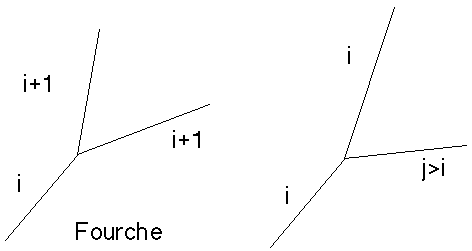
Image002.gif (2567 octets)

Biordre (i+1,i+1) Biordre (i,j)

Figures 4B et 4C : Biordres

Considérons l'évolution au cours du temps d'une arête quelconque d'ordre i. Cette arête doit donner naissance au cours de la génération ("année") i à deux arêtes qui adopteront comme couple d'ordres, appelé "biordre d'évolution" la valeur (d,g). Comme défini au paragraphe 4.2.1.1, on aura obligatoirement d = i et g = i. Plus précisément le choix de ce biordre devra s'effectuer parmi les couples d'entiers suivants ou leurs symétriques: (i+1,i+1), (i,i+1), (i,i+2), ..., (i,+8) (Figures 4B et 4C).

4.2.2 Matrice d'évolution pour la génération d'un arbre binaire

On associe à chacun de ces biordres d'évolution une probabilité d'apparition dans l'arbre dont on désire modéliser la croissance, probabilité notée pi,j, pour les biordres (i,j) avec j>i, et pi,i pour les biordres (i+1,i+1). On définit ainsi une matrice d'évolution (pi,j)i³1,j³1 dont la ligne i donne les probabilités d'apparition des biordres issues des arêtes mères d'ordre d'évolution i .Cette matrice est triangulaire supérieure (table 4A), infinie dans les deux directions et évidemment stochastique (la somme des valeurs comprises sur chaque ligne est égale à 1).

Image003.gif (3249 octets)

Table 4A : Un exemple de matrice d'évolution

4.2.3. Algorithme de synthèse de la croissance par matrice d'évolution

L'intérêt de cette modélisation topologique est d'autoriser un phénomène discret de croissance. A chacune des étapes de la croissance, l'arbre obtenu pourra être représenté, pour obtenir une prévisualisation d'un instant donné. Les planches 3, 4 et 9 donnent des exemples d'application de l'algorithme 1 de croissance d'une arborescence.

L'algorithme 1 de génération est le suivant:

Algorithme 1 (de génération) :

Au départ, l'arbre est constitué d'une seule arête (son arête racine) d'ordre d'évolution 1 et est dit d'âge 1.

A la "génération" I (³1), qui permet de passer d'un arbre d'âge I à un arbre d'âge I+1, on détermine toutes les branches de l'arbre d'ordre d'évolution I, et on les fait évoluer à l'aide de la ligne I de la matrice d'évolution en des arêtes d'ordre ³ I+1 : quand on a trouvé, une arête d'ordre I que l'on sait devoir modifier, on utilise la matrice d'évolution pour choisir en respectant les probabilités de la ligne I un biordre (J,I) avec J>I ou le biordre (J=I+1,I+1), et générer ainsi deux nouvelles arêtes d'ordres J et I ou I+1 et I+1. La génération I est terminée lorsqu'il n'existe plus d'arête terminale d'ordre d'évolution I dans l'arbre. Ceci implique que les arêtes d'ordre d'évolution I apparues au cours de la génération I soient également traitées au cours de cette génération : on constate donc que l'arête d'ordre I de départ a conduit à la génération I à la création d'un segment d'ordre I qui se termine sur un biordre (I+1,I+1).

Implantation

La croissance aboutissant à un arbre de N+1 "années", sera donc réalisée par une itération pour I de 1 à N de la génération I. A chaque génération I, on devra trouver toutes les arêtes d'ordre I pour les faire ramifier en arêtes d'ordre supérieur ou égal à I+1. Une première solution consiste à reparcourir l'arbre en entier à chacune des itérations afin de trouver toutes les arêtes concernées, une meilleure solution consiste à chaîner au cours de l'évolution toutes les arêtes ayant un même ordre J, pour tout J. A la génération I, il suffira alors de traiter les arêtes du chaînage liant les arêtes d'ordre I, ainsi que les nouvelles arêtes d'ordre I qui apparaîtront au cours de ce traitement par la création de biordres (J>I,I). Cette seconde méthode à l'avantage d'éviter un parcours multiple de l'arbre, mais en revanche il devient nécessaire de gérer les listes chaînées correspondant à chacun des ordres.

4.2.4 Sous-matrice d'évolution d'ordre N d'une matrice d'évolution

Dans la pratique, on ne peut pas stocker une matrice d'évolution M infinie. Si l'on connaît le nombre maximum N de générations à réaliser, il suffira de stocker la sous-matrice carrée d'ordre N de la matrice d'évolution en y adjoignant une N+1ème colonne (de hauteur n) constituée de la somme des colonnes N+1 à de la matrice d'évolution. L'élément sur la ligne i (1£i£N) de cette N+1ème colonne, noté pi,³N+1 représente pour i fixé, la probabilité d'apparition d'un biordre (i,j) avec j³N+1.

On déduit facilement de l'algorithme 1 que cette sous-matrice (toujours stochastique), appelée sous-matrice d'évolution d'ordre N de M et notée M_£N dans la suite, contient toutes les informations nécessaires aux N premières générations d'un arbre binaire selon la matrice M. En effet, les nœuds d'ordre d'évolution strictement supérieur à N générés au moyen de la N+1ème colonne au cours de la croissance n'évolueront pas au cours des générations d'indices inférieurs ou égaux à N. Leurs ordres nous importent peu pourvu qu'ils soient strictement supérieurs à N.

D'autres solutions de stockage économique sont possibles:

- dans le cas particulier où le terme courant pij de la matrice est la valeur f(i,j) en i et j d'une fonction discrète f, seule la programmation de cette fonction est alors nécessaire,

- dans le cas de l'autosimilarité, c'est à dire dans le cas où toutes les lignes de la matrice source sont identiques à un décalage près, on ne stocke alors qu'une seule ligne au lieu de toute la matrice.

4.3. Problèmes liés à l'analyse inverse de la croissance d'une structure arborescente donnée

Les modèles de physique concernant les structures ramifiées arborescentes rencontrées dans la nature (Par exemple les éclairs électriques, Niemeyer, Pietronero, Wiesman [NP84], la "digitation visqueuse", Nittmann, Daccord, Stanley [ND85], VanDamme et al. [VO86], les précipités de métal électrolytique, Sawada, Dougherty, Gollub [SD86] ou les bien connus "Diffusion Aggregation Process (DLA)" de Witten & Sanders [WS81], et Ball [Ba86]) sont considérés ou approximés par des structures ramifiées fractales. Leur aspect visuel est mesuré par les physiciens avec un nombre unique : la dimension fractale (voir Mandelbrot [Ma82]), et dans Vannimenus, Viennot [VV89], Vannimenus [Va87], par un tableau de nombres : la matrice de ramification associée (cf chapitre 3).

Un problème plus complexe, incluant le précédent de la mesure de la forme, est celui de la caractérisation de la croissance d'une structure arborescente : le fait que la forme est implicitement contenue dans l'historique de l'arbre est un concept bien connu en botanique, D'Arcy Thompson [Ar52], Hallé, Oldeman et Tomlinson [HO78]. Il se décompose en deux aspects que nous abordons aux deux paragraphes suivants :

Soit T une arborescence binaire topologique donnée :

Problème 1

En supposant que la croissance de T ait eu lieu dans notre modèle, peut-on alors retrouver cette croissance passée de T?

Précisément :

(1) Peut-on déterminer, l'âge inconnu a = a(T) de T (et donc le nombre de générations g(T) = a-1) ainsi que tous les arbres des générations précédentes ayant conduit à T dans notre modèle?

(2) Peut-on trouver la sous-matrice d'évolution M_£g(T) d'ordre g(T) ayant piloté la croissance de T?

Problème 2

La croissance de l'arborescence binaire T étant due à un processus physique ou mathématique (cf ci-dessus et paragraphe 4.4), existe-t-il une matrice d'évolution M permettant de modéliser la croissance réelle passée de T (Hypothèse préliminaire au problème 1) et de prévoir sa croissance future?

4.3.1. Algorithme de reconstruction de la croissance passée d'une arborescence

La réponse au problème 1 est positive et est donnée par l'algorithme 2 :

Algorithme 2

Comme conséquence de l'algorithme 1 de génération, on affecte aux feuilles de T dont le noeud frère est une feuille, l'ordre a (=a(T)); on sait que les autres feuilles ont un ordre ³a (cf figure 4D).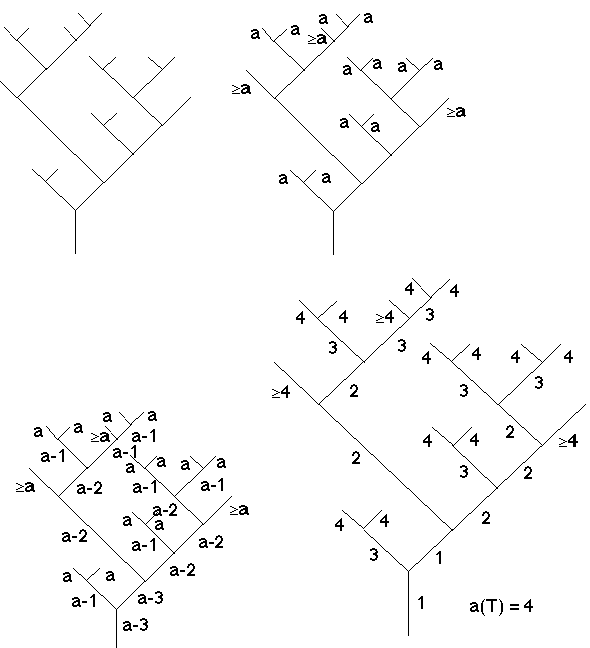

Image005.gif (8813 octets)

Figure 4D: Reconstruction des ordres d'évolution en fonction de l'âge a = a(T) de l'arbre T.

On déduit de cette reconstruction que a(T) = 4 et g(T) = 3.

Par ailleurs, l'algorithme 1 nous indique alors que l'ordre d'un noeud interne est le plus petit des ordres de ses fils lorsque ceux-ci sont différents, ou leur ordre commun diminué d'une unité sinon. C'est ce qu'exprime la fonction récursive Ordre ci-dessous (en tenant compte du fait que si un seul des deux fils est une feuille, donc d'ordre = a, son frère (noeud interne) est d'ordre =a-1 et a donc nécessairement le même ordre que son père).

Fonction Ordre (n : noeud interne);
  Si un seul des fils de n, noté f, est interne alors
    Ordre(n) := Ordre(f)
    sinon
    Si Ordre(fils_gauche) = Ordre(fils_droit) alors
      Ordre(n) := Ordre(fils_gauche) - 1
      sinon
      Ordre(n) := min(Ordre(fils_gauche),Ordre(fils_droit))
      fsi
    fsi
  fin

Dès lors, par l'appel de la fonction récursive Ordre (racine), on détermine en fonction de a (sous la forme a-k : voir figure 4D), les ordres de tous les noeuds internes de l'arbre T. Sachant que l'ordre d'évolution de la racine est 1, on en déduit a(T), g(T) puis tous les ordres des noeuds de T, à l'exception des ordres des nœuds terminaux dont le nœud frère n'est pas terminal pour lesquels on ne connaît que la borne minimale a(T). Il est alors facile par l'algorithme 1 de déterminer toutes les étapes de la croissance de T (Figure 4E).

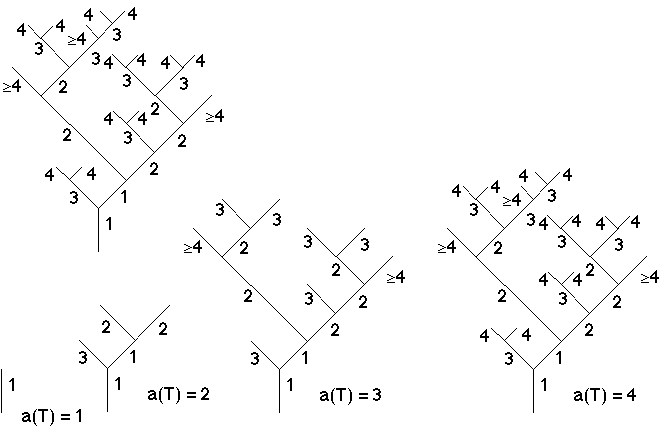
Image006.gif (6769 octets)

Figure 4E: Exemple de la reconstruction de la croissance passée de l'arbre binaire de la figure 4A (dont on aurait oublié les ordres: comparer les ordres reconstruits à ceux donnés figure 4A).

4.3.2 Estimation de la sous-matrice d'évolution M£g(T) de T

On obtient alors une estimation statistique de la sous-matrice d'évolution M_£g(T) d'ordre g(T) de T (Figure 3) en remplaçant chaque quantité inconnue pi,j (j³i) par la valeur estimée constituée par la proportion des biordres (i,j) ou (biordres (i+1,i+1) dans le cas j=i) parmi ceux d'arête mère d'ordre i dans l'arbre T. Précisément :

- pour 1£i£g(T) : ai est le nombre de nœuds internes d'ordre d'évolution i

- pour i<j£g(T) : bij est le nombre de biordres d'évolution (i,j)

- pour 1£i£g(T) : bii est le nombre de biordres d'évolution (i+1,i+1)

bi,a est le nombre de biordres d'évolution (i,=a(T)) (Figure 4F)

- pour i£j£a(T) : pij = bij / ai.

Pour que cette estimation statistique soit significative, il faut disposer pour chaque ligne i d'un nombre important de biordres (loi des grands nombres). Ce sera le cas pour tous les termes de la matrice (voir paragraphe 4.4 pour des exemples) si l'on dispose d'un nombre important d'arbres T générés aléatoirement dans les mêmes conditions. Alors qu'il peut y avoir un problème pour la première ligne de la matrice (biordres(1,j)) dans le cas où l'on ne dispose que d'un seul arbre T (insuffisance du nombre de biordres).

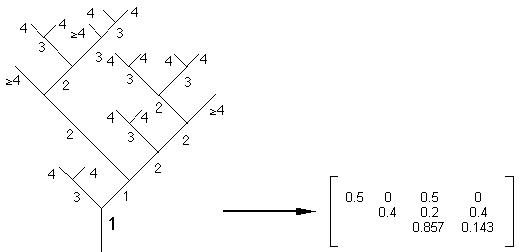
Image007.gif (3281 octets)

Figure 4F: Extraction de la sous-matrice d'évolution M=3 de l'arbre T de la figure 4E.

4.3.3 Lien entre une technique de croissance et ce modèle d'évolution

Ce problème se pose lorsque l'on dispose d'une technique (physique ou mathématique par exemple) de génération d'arbres binaires d'une certaine classe. Pour y répondre, on génère un nombre important d'arbres de taille (nombre de nœuds internes par exemple) donnée n. Si l'on suppose qu'il existe une matrice d'évolution M permettant de guider cette croissance, on peut déterminer par l'algorithme 2 d'extraction et le paragraphe 4.3.2, la sous-matrice d'évolution estimée M_£g (n) (où g est le minimum des nombres de générations associés aux arbres de taille n générés).

Lorsque, pour n tendant vers l'infini, toutes les sous-matrices d'évolution M_£g (n) apparaissent comme sous-matrices d'une même matrice d'évolution M limite, on considérera avoir répondu positivement au problème 2 pour la technique de génération étudiée.

En l'état, il n'est pas possible d'effectuer de prévisions sur les générations futures de l'arborescence car les lignes suivantes de la matrice ne sont pas connues. Mais, si l'évolution des lignes de la matrice limite trouvée laisse entrevoir la possibilité d'extrapoler de nouvelles lignes à partir de celles déjà établies, le cas le plus simple étant celui où il y a manifestement auto-similarité, il est possible de prévoir l'évolution future des arbres générés par le modèle mathématique ou physique considéré.

Nous donnons quelques exemples de matrices d'évolution extraites à partir de techniques de génération mathématiques d'arbres topologiques binaires aux paragraphes suivants.

4.4 Exemples de matrices d'évolution

4.4.1 Arbre parfait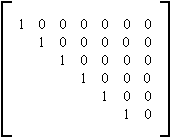

Image008.gif (1772 octets)

Table 4C : Matrice d'évolution des arbres binaires parfaits

La matrice d'évolution générant la croissance des arbres parfaits est la matrice identité infinie. En effet, lors de la génération I de la croissance, toute arête feuille a pour ordre d'évolution I et se ramifie avec probabilité 1 en deux arêtes d'ordre I+1. A chaque génération, la profondeur de l'arbre parfait augmente d'une unité. La taille de l'arbre est ainsi multipliée par deux à chaque itération. La table 4C montre la matrice ainsi obtenue. Un exemple d'évolution obtenue au moyen de cette matrice est fourni à la photographie 4A.

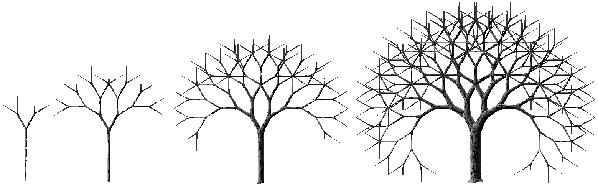
Photographie 4A: Evolution d'un arbre parfait

4.4.2 Arbre binaire aléatoire

L'arbre binaire aléatoire a été défini au paragraphe 3.2.4.4.2. La table 4D donne la sous-matrice d'évolution M=8 calculée statistiquement sur des arbres de taille 30000 et d'âge 9, construits en utilisant l'algorithme de génération proposé dans Remy [Re84].

Age 3 Age 5 Age 6

Photographie 4B: Evolution d'un arbre binaire aléatoire

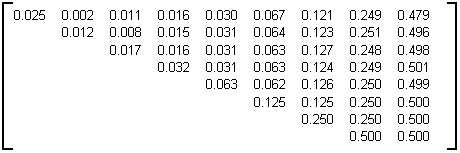
Image009.gif (3677 octets)

Table 4D: Matrice d'évolution statistique des arbres binaires aléatoire de taille 30000 et d'âge 9

Il est à noter que dans cet exemple, lorsque la taille fixée n des arbres varie, la sous-matrice d'évolution obtenue n'est pas stable et il n'y a pas convergence vers une matrice limite M lorsque n croît. En particulier, lorsque la taille n des arbres binaires aléatoires générés augmente, les éléments sur la diagonale tendent vers 0 (sauf pour la première ligne). Aussi la matrice donnée table 4D n'est adaptée que dans le cadre où elle a été obtenue, c'est à dire pour la génération d'arbres binaires aléatoires de taille 30000 noeuds internes et d'âge 9. Des exemples de générations d'arbres binaires aléatoires par cette matrice sont présentés à la photographie 4B et à la planche 3.

4.4.3 Arbre binaire aléatoire croissant

La sous-matrice d'évolution M=9 moyenne calculée statistiquement à partir d'un échantillon de 1000 arbres binaires aléatoires croissants (voir algorithme de construction donné au paragraphe 3.2.4.4.3) de 32000 nœuds internes d'âge 10 est donnée en table 4E.

Différents autres tests avec 1000, 3000, 5000, 9000 et 11000 noeuds ont montré une remarquable compatibilité des sous-matrices d'évolution obtenues. On déduit de ce résultat que la croissance des arbres binaires aléatoires croissants telle que définie au paragraphe 3.2.4.4.3, est proche de celle définie dans note modèle par la matrice d'évolution de la table 4F. Les lignes retenues pour le calcul de la matrice limite table 4F sont les lignes intermédiaires de la matrice moyenne extraite, c'est à dire les lignes qui ne sont pas modifiées si on fait varier la taille des arbres générés.

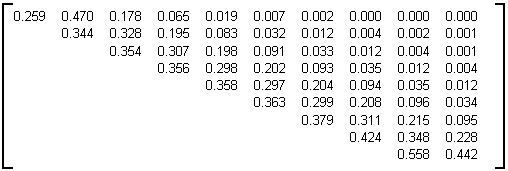
Image010.gif (4174 octets)

Table 4E: Matrice d'évolution statistique des arbres binaires aléatoire croissants de 32000 nœuds

Les premières lignes ne sont pas représentatives en raison de fluctuations dues à la taille des arbres générés. Ce sont ces lignes qui varient progressivement quand on fait varier le nombre de nœuds de l'arbre généré. Si la taille augmente, les coefficients sur la diagonale diminuent tandis que les autres valeurs augmentent en proportion. Les dernières lignes sont elles aussi modifiées si on génère des arbres plus gros, mais pour une raison différente: à force d'augmenter la taille des arbres générés, les arbres créés ne sont plus d'âge 10 mais des arbres d'âge 11. Il y a alors décalage global de la matrice d'une ligne vers le bas et création d'une nouvelle première ligne (Il est à signaler que si l'on génère des arbres binaires aléatoires croissants de taille 32000 on obtient 56% d'arbres d'âge 10 et 44% d'arbres d'âge 11).

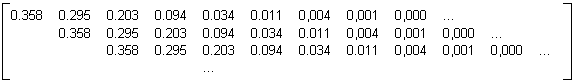
Image011.gif (2663 octets)

Table 4F : Matrice d'évolution limite des arbres binaires aléatoires croissants

Des exemples d'évolutions d'arbres binaires aléatoires croissants générés au moyen de cette matrice d'évolution sont fournis à la photographie 4C et à la planche 4. Ces arbres présentent le port caractéristique des arbres binaires aléatoires croissants.

La planche 9 montre également la croissance d'arbres binaires aléatoires croissants, mais avec une géométrie permettant de prendre en compte des effets de phototropisme ou d'attraction dans une direction donnée (cf paragraphe 4.2.4).

Age 2 Age 3 Age 4 Age 5 Age 6 Age 7

Age 8 Age 9

Photographie 4C: Evolution d'un arbre binaire aléatoire croissant

4.4.4 Tries

La table 4G a été extraite à partir d’un échantillon de 1000 Tries (définition au paragraphe 3.2.4.4.4) d’âge 11 tels que card(w) = 8000, s = 14. La photographie 4D montre l’évolution de cette classe d’arbres aux générations 2, 4, 6 et 8. De toute évidence de tels arbres restent extrêmement réguliers tout au long de leur croissance. Il est difficile d'établir la convergence ou la non-convergence de la matrice extraite car la taille des arbres générés est fonction des deux paramètres card(w) et s. En fait la forme des arbres générés varie suivant les valeurs de ces deux paramètres : plus card(w) augmente ou plus s diminue plus la sous-matrice d'évolution extraite se rapproche de la matrice identité.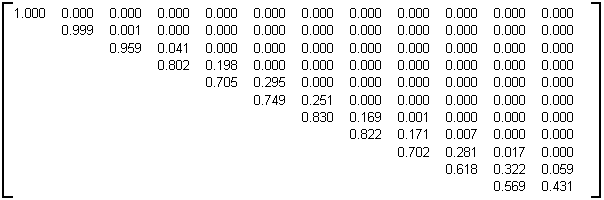

Image013.gif (4847 octets)

Table 4G : Sous-matrice d'évolution statistique M=11 des tries de card(w) = 8000 et s = 14.

Photographie 4D: Evolution d'un trie (Ages 3, 5, 7 et 9).

4.4.5 Auto-similarité

La matrice d'évolution présentée table 4A ou 4F est auto-similaire. Par cela, nous entendons que les variations des probabilités de biordre sur chacune des lignes sont identiques a un décalage près (elles commencent toutes sur la diagonale). En d'autres termes, si nous visualisons cette variation par une courbe extrapolant les points (j-i,pi,j) pour j³i, toutes les courbes associées à chaque ligne sont identiques. Une telle matrice sera donnée dans la suite par sa première ligne.

4.5 Modèles géométriques

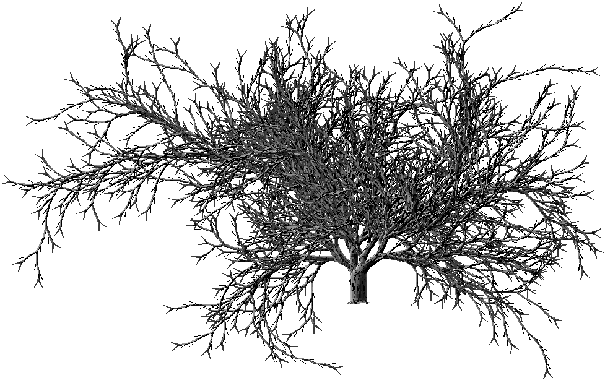
Photographie 4E: Propriétés des lois géométriques au cours de l'évolution d'un nouvel arbre binaire aléatoire croissant

On suppose disposer d'un arbre topologique binaire T dont chaque arête possède un ordre d'évolution entier.

La géométrie de l'arbre est parfaitement définie si on connaît la position de tous les nœuds et l'épaisseur de toutes les arêtes. Dans la pratique une arête est géométriquement définie :

- en 2D par la position 2D du point figurant sa racine et par la donnée d'un angle: son angle d'orientation dans le plan de représentation.

- en 3D par la position du point figurant sa racine et par la donnée de deux angles : un premier angle déterminant la projection p de l'arête donnée sur le plan xOy (figurant le "sol") et un second angle par rapport à la verticale Oz permettant de déterminer la direction de l'arête donnée dans le plan (p,Oz).

Le calcul des longueurs et des angles de déviation de chacune des deux arêtes filles (deux fois un angle en 2D, deux fois deux angles en 3D) est réalisé selon les règles dépendant des ordres d'évolution, données aux paragraphes suivants. Cependant, les ordres d’évolution étant fixés une fois pour toutes, les longueurs, épaisseurs et angles de déviations seront toujours identiques, quelque soit l'âge de l'arbre, alors que dans la réalité, la croissance d'un arbre présente certaines caractéristiques fonctions de son âge :

- Les épaisseurs des branches augmentent années après années (Photographie 4E).

- Les longueurs des branches d'un arbre augmentent (assez peu) d'une année par rapport à la précédente (la croissance d'un arbre botanique s'effectuant surtout par génération de nouvelles branches à chaque printemps).

Pour tenir compte de ces phénomènes, on utilise l'âge de l'arbre comme paramètre supplémentaire pour l'établissement de la formule de calcul définissant l'épaisseur et la longueur.

4.5.1 Calcul des épaisseurs et des longueurs

Les formules de calcul des épaisseurs et des longueurs pour les modèles 2D et 3D doivent impérativement être positives décroissantes de l'ordre d'évolution (éventuellement constante pour la loi de longueur). On utilise des fonctions linéaires, quadratiques, polynomiales ou exponentielles de l’ordre d'évolution k de l’arête considérée, du type :

L(k) = c1 + c2 * k’ + c3 * k’²

E(k) = ce * k’^a ou E(k) = ce * ß^k’

avec :

k’ = max(1,âge(T) - k + 1), L(k) et E(k) longueur et épaisseur de l'arête considérée, c1, c2, c3, ce, a et ß des coefficients numériques constants.

Ces fonctions sont bien positives, décroissantes de l'ordre d'évolution k d'une arête. Elles sont de plus croissantes de l'âge de l'arbre.

4.5.2 Géométrie 2D

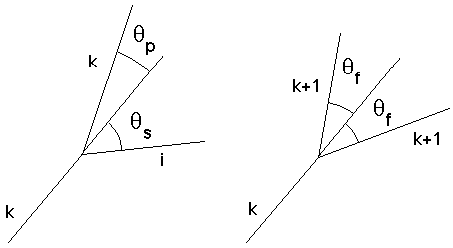
Image014.gif (2820 octets)

Figure 4G: Angles qf, qp et qs en fonction du biordre d'évolution

Pour chacune des branches filles, nous avons à définir un angle de déviation par rapport à la branche mère. Ces angles dépendent des valeurs des ordres d'évolution k et k+i, i=1, (ou dans le cas d'une fourche: k+1 et k+1) de chacune des branches filles, lorsque la branche mère est d'ordre k. Il est en effet logique de penser qu'à un embranchement donné, la branche la plus importante (celle d'ordre k minimum) sera moins déviée que la branche secondaire (celle d'ordre k+i ). Ce qui nous conduit à des formules pour un biordre d'évolution (k,i), k<i, du type suivant :

qp(k,i) = qs(k,i) = qf =

où qm, qs et qf sont les angles de déviation des branches principales, secondaires et des fourches, cp, cs, cf des coefficients numériques.

4.5.3 Géométrie 3D

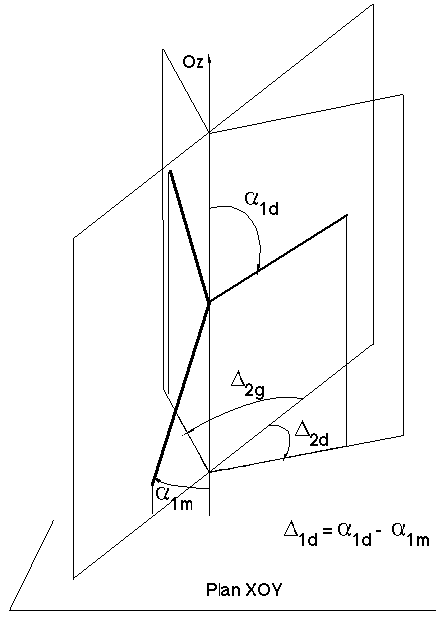
Image018.gif (7461 octets)

Figure 4H : Définition des angles 3D

Le modèle géométrique 3D est, de la même manière qu'au paragraphe précédent, directement issu du modèle 3D développé dans le cadre des matrices de ramification (voir paragraphe 3.4.3). Les angles ?1 de déviation par rapport à la verticale et les angles ?2 de déviation en projection dans le plan xOy répondent aux mêmes formules que celles du paragraphe précédent (Figure 4H) :

D1p(k,i) =

D1s(k,i) =

D1f(k,i) = Cf

D2p(k,i) = + Inc(a1(mère))

D2s(k,i) = + Inc(a1(mère))

D2f(k) = Cf + Inc(a1(mère))

La fonction incertitude Inc n'a pas a être modifiée car elle ne fait pas intervenir les ordres ou les biordres des nœuds mais seulement un angle.

Le modèle 3D incluant une composante aléatoire dans le calcul des déviations angulaires en projection dans le plan xOy, il est nécessaire d’effectuer un certain nombre de manipulations (en particulier des sauvegardes intermédiaires des angles) pour retrouver strictement les mêmes angles pour les mêmes branches pour toutes les générations de la croissance.

4.5.4 Orientation de la structure et effets spéciaux

Dans le cas d'un biordre (k,k+i) avec i³1, il faut préciser pour chaque choix d'angle de déviation (un choix en 2D et deux choix en 3D) laquelle des deux arêtes (principale ou secondaire) part à droite par rapport à la branche mère.

Il y a essentiellement quatre options possibles. La première possibilité est d'effectuer ce choix aléatoirement (équi-probabilité pour chaque coté). La seconde option est d'alterner les arêtes principales tantôt à droite, tantôt à gauche sur chaque segment de l'arbre. La troisième option est de fixer le choix de telle manière que l'arête principale soit toujours du même coté, cela pourra donner une simulation de l'effet du vent ou de la gravité sur l'image finale de l'arbre. La dernière option consiste à choisir l'orientation pour que l'arête principale soit plus proche que l'autre arête d'une direction prédéfinie (attraction dans une direction donnée, voir planche 4) comme par exemple la verticale (effet de phototropisme, voir planche 9).

La modélisation 3D et le rendu des images seront développés au chapitre 7, partie 3.

4.6 Influence de la matrice d'évolution sur la topologie, la géométrie et la croissance

La matrice d'évolution permet de contrôler la synthèse de la croissance d'un arbre sur de nombreux plans:

4.6.1 Calcul de la taille d'un arbre à partir de sa sous-matrice d'évolution

Le problème proposé est identique dans sa formulation à celui du paragraphe 3.5.6 : à partir d'une matrice d'évolution M (infinie dans les deux directions), est-il possible de déterminer les tailles moyennes des arbres binaires de la suite d'arbres TAGE (AGE ³ 2) générés au moyen de cette matrice? La réponse est positive, la méthode de calcul est voisine de celle du paragraphe 3.5.6.

Soit une matrice d'évolution M (triangulaire supérieure). Cette matrice contient les probabilités d'apparition pj,j des biordres (i,j) lors de la génération (pj,j est associée aux biordres (j+1,j+1)).

Le calcul consiste à trouver les nombres moyens nj,i (1£j£i) de biordres générés par utilisation de cette matrice, et par somme de ces nombres moyens, le nombre moyen de nœuds internes contenus dans l'arbre. Comme dans le paragraphe 3.5.6, on obtient les résultats suivants :

Longueur moyenne d'un segment d'ordre j

La longueur moyenne d'un segment d'un segment d'ordre j est notée Lj.

Lj = (1) (voir paragraphe 3.5.6)

Nombre moyen de nœuds de biordre (j,i) sur un segment d'ordre j (j < i)

i > j (2)

Nombre moyen de segments d'ordre j

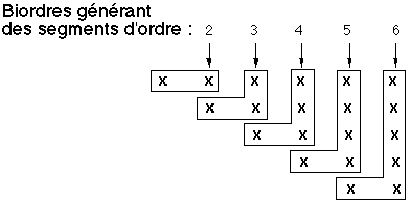
Image021.gif (3486 octets)

Figure 4I: Calcul des nombres de segments d'ordre

Le nombre moyen nj,j de segments d'ordre j (égal au nombre de biordres (j+1,j+1) qui sont les biordres terminaux de ces segment) est égal à la somme des nombres d'apparition des biordres (k,i) tels que j = k ou j = i (les biordres (j,j) étant comptés doubles). On comptabilise ainsi le nombre de nœuds d'ordre j qui sont les premiers nœuds d'un segment d'ordre j. Les nombres recherchés sont donc nj-1,j-1 correspondant au biordre (j,j) et comptés doubles, n1,j, n2,j, ..., nj-1,j (voir figure 4I). Ce qui conduit à la formule:

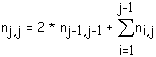Image022.gif (1227 octets) (3)

La valeur n1,1 n'est pas calculable par cette formule. Elle est égale à 1, car n1,1 représente le nombre de segments d'ordre 1.

Nombre moyen de nœuds de biordre (j,i) (1 £ i < j)

nj,i = hj,i * nj,j = i > j (4)

Nombre total moyen de nœuds internes

Le nombre moyen de nœuds internes de T_AGE est égal à la somme des nombres moyens de biordres calculés par les formules ci-dessus :

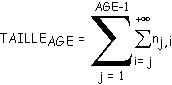Image022.gif (1227 octets) (5)

Comme dans le cas des matrices de ramification, on constate une grande fluctuation de la taille des arbres obtenus en raison du caractère stochastique du tirage des probabilités sur les lignes de la matrice d'évolution source pendant la croissance de l'arbre. Mais les moyennes déterminées par calcul correspondent bien aux moyennes expérimentales (Tableaux 4H et 4I).

Matrice	Age	Nombre d'arbres	Taille moyenne calculée	Taille moyenne observée
Table 4D	4	46000	565,49	561,06
Table 4E	6	86000	463,98	463,88
Table 4F	9	120000	506,05	505,84

Tableau 4H : Tailles moyennes calculées et observées.

Age	Taille moyenne calculée	Taille moyenne observée
2	2,793	2,789
3	10,68	10,69
4	34,54	34,59
5	107,13	107,33
6	327,99	327,41
7	999,97	1000,22

Tableau 4I : Tailles moyennes calculées et observées sur 150000 arbres générés par la matrice 4F.

Remarque

A partir de la sous-matrice d'évolution M (de dimension (A,A+1) avec A = âge(T)-1) extraite d'une arborescence binaire T quelconque, il est possible de retrouver la taille de l'arbre T tout au long de sa croissance, les calculs des formules précédentes étant alors entiers.

Exemple

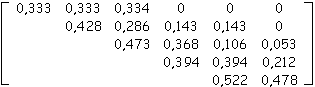
Image025.gif (2192 octets)

Soit la sous-matrice d'évolution extraite à partir d'un arbre topologique binaire quelconque généré par matrice d’évolution et dont on suppose ne pas connaître la taille :

De proche en proche, nous allons calculer tous les nombres de biordres.

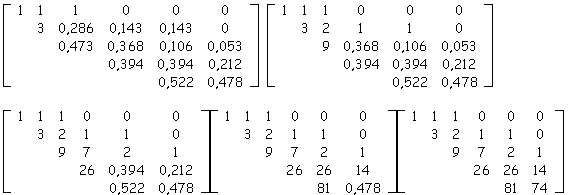
Image026.gif (4805 octets)

La somme des nombres de biordres nous permet de conclure que la taille de l'arbre aux âges 2, 3, ..., 6 était de 3, 10, 29, 95 et 250 nœuds internes (sommes respectives des entiers sur la première, les 2,..., 5 premières lignes de la matrice d'entiers reconstruite).

4.6.2 Au niveau topologique

4.6.2.1 Influence des valeurs contenues sur la diagonale

Une diagonale forte (voir la table 4C associée à la photographie 4A pour les arbres parfaits ou encore la table 4E avec la photographie 4C correspondant aux arbres binaires aléatoires croissants) permet de générer des arbres bien équilibrés, de formes d'autant plus proches de celle de l'arbre parfait que le poids de la diagonale est élevé (c'est ce que l'on constate en comparant un Trie de la photographie 4D obtenu avec la matrice de la table 4G et un arbre binaire aléatoire croissant de la photographie 4C). L'explication vient du fait que la longueur moyenne des segments d'ordre d'évolution k est égale au rapport : moyenne de la variable aléatoire discrète de loi: (i, pk,k(1-pk,k)^i-1)iŒN* (Paragraphe 3.5.6). Dès lors, plus le coefficient pk,k est proche de 1, plus la longueur du segment d'ordre k est également proche de 1, limite qui caractérise les arbres parfaits.

Au contraire, par le même raisonnement, une valeur faible sur la diagonale de la ligne k (table 4D avec la photographie 4B pour les arbres binaires aléatoires) conduit à l'apparition de longs segments d'ordre k. Ainsi une matrice avec une diagonale uniformément faible conduira à un arbre décharné, contenant de longs segments de tous ordres: c'est le cas des arbres binaires aléatoires de la photographie 4B.

Ces cas extrêmes permettent ainsi de préciser les rôles relatifs de la diagonale et du reste de la matrice d'évolution dans la forme de l'arbre topologique obtenu. Un choix approprié de ces probabilités permet de jouer sur la longueur des segments, permettant ainsi d'obtenir une grande variété de formes synthétisées.

4.6.2.2 Influence de la répartition des valeurs sur les lignes (hors diagonale)

La présence de valeurs importantes sur les premières sur-diagonales entraîne la génération d'arêtes latérales d'ordres légèrement plus grands que celui du segment sur lequel elles sont placées. Ces arêtes évoluent très peu de générations après la création du segment (immédiatement après pour celles d'ordre k+1 si k était l'ordre du segment créé). En conséquence l'arbre généré au cours de l'évolution sera beaucoup plus touffu si les valeurs sur les premières sur-diagonales sont grandes car les sous-arbres introduits croissent alors très vite.

4.6.3 Au niveau de la vitesse de croissance

4.6.3.1 Influence des valeurs sur la diagonale

Plus les valeurs sur la diagonale sont grandes (proches de 1), moins la taille de l'arbre généré grandira vite. Si on prend par exemple deux matrices autosimilaires M1 et M2 de lignes caractéristiques respectives L1 = (0.2,0.8,0,0...) et L2 = (0.33,0.67,0,0,..), le tableau 4J donne les tailles moyennes (calculées au moyen des formules théoriques ci-dessus) des arbres générés au moyen de ces deux matrices pour les générations 1 à 7. On constate une très grande différence entre les vitesses de croissance même si les valeurs sur les diagonales semblent assez voisines.

La raison de cette différence de vitesse de croissance est simple: plus la diagonale est forte, plus la longueur moyenne des segments est proche de 1, en conséquence de quoi plus ils sont petits et plus le nombre de segments latéraux auxquels ils donnent naissance est petit, donc plus la taille de l'arbre résultant est petite. Ce phénomène se produit à chaque génération.

	Matrice M1	Matrice M2
Age 1	1	1
Age 2	5	3
Age 3	35	15
Age 4	215	63
Age 5	1295	255
Age 6	7775	1023
Age 7	46655	4095
Age 8	279935	16385

Tableau 4J: Evolution de la taille des arbres en fonction de matrices d'évolution

L'explication mathématique est que dans les formules du paragraphe 4.5.6, les probabilités pi,i sont placées au dénominateur. Donc, plus elles sont faibles, plus la taille théorique de l'arbre généré sera grande, entraînant une vitesse de croissance elle même plus grande.

4.6.3.2 Influence des valeurs sur les sur-diagonales

Considérons les deux matrices d'évolution auto-similaires M1 et M2 qui ont pour lignes de probabilités caractéristiques respectives L1 = (0.25,0.75,0,0,...) et L2 = (0.25,0,0,0.75,0,0,..). Les arbres topologiques obtenus (Photographie 4F, lois géométriques identiques) à partir de ces deux matrices d'évolution après 4 générations pour M1 et 7 générations pour M2 se ressemblent: ils présentent tous deux d'assez longs segments (longueur moyenne 4) dus à une valeur de diagonale faible identique et ont a peu près le même développement. Ils possèdent respectivement 843 et 1122 nœuds internes sur notre exemple, la taille théorique calculée au vu des matrices étant de 624 pour M1 et 1132 pour M2 comme le montre le tableau 4K. Ceci implique que l'arbre associé à la matrice M2 a une croissance beaucoup moins rapide que celui associé à la matrice M1.

Photographie 4F: Influence du contenu des lignes sur la vitesse de croissance

	M1 Taille théorique	Arbre gauche Figure 4F, matrice M1	M2 Taille théorique	Arbre droit Figure 4F, matrice M2
Age 1	1	1	1	1
Age 2	4	5	4	4
Age 3	24	32	12	12
Age 4	124	165	28	26
Age 5	624	843	72	68
Age 6	3124		184	183
Age 7	15624		456	441
Age 8	78124		1132	1122
Age 9	390624		2820

Tableau 4K : Evolution de la taille des arbres en fonction de matrices d'évolution

Ce différentiel de vitesse de croissance s'explique par le fait que dans la matrice M2 les biordres autres que diagonaux sont du type (k,k+3). Toute branche fille latérale d'ordre k+3 apparaissant à la génération k attend trois nouvelles générations pour se développer. Ce n'est pas le cas dans le cas de la matrice M1 où tous les biordres autres que diagonaux sont du type (k,k+1), ce qui implique l'évolution de toute branche nouvellement créée, soit immédiatement, soit à la génération suivante. La longueur moyenne des segments étant identique, l'arbre de la matrice M1 doit obligatoirement évoluer plus vite que celui de la matrice M2, ses nœuds évoluant plus vite.

On voit ainsi qu'apparaît naturellement dans ce modèle un phénomène bien connu en botanique : la dormance. La durée de dormance d'une feuille d'ordre J dont le père est d'ordre I (=J) sera définie égale à J-I (nombre de générations pendant laquelle cette feuille n'évoluera pas).

4.6.4 Au niveau géométrique

La partie au dessus de la diagonale de la matrice d'évolution a également une influence sur la géométrie de l'arbre (manière avec laquelle l'arbre est dessiné): les deux arbres de la photographie 4F, sont topologiquement proches mais se distinguent au niveau géométrique par l'épaisseur des branches secondaires (dans les branchements autres que fourches). Cette épaisseur est beaucoup plus faible que l'épaisseur de la branche mère dans le cas de la matrice M2 (à droite) alors qu'elle en est très voisine dans le cas de la matrice M1 (à gauche).

Cela s'explique par le fait que l'épaisseur est une fonction décroissante de la variable ordre (voir paragraphe 4.5.1). Aussi, dans le cas de la matrice M2, les branches secondaires étant d'ordre k+3 par rapport à la branche mère d'ordre k, leur épaisseur dans le cas du choix d'une fonction du type: épaisseur = C(Age-k), sera C3 fois plus petite que la branche mère (dans le cas de la photographie 4F, 1.6³ = 4.0), alors que dans le cas de la matrice M1, ce facteur de réduction sera C. La même type de remarque à caractère purement géométrique est valable en ce qui concerne les longueurs des branches si la loi adoptée pour leur calcul n'est pas constante (ce qui est le cas sur la photographie 4F).

La géométrie de l'arbre est donc non seulement influencée par le choix des lois géométriques et de l'orientation de la structure, mais également par la matrice d'évolution qui est un objet combinatoire.

4.6.5 Mélange de matrices et croissance non auto-similaire

Le mélange de matrices d'évolution consiste à former une nouvelle matrice à partir de lignes d'autres matrices. Les i1 premières lignes proviennent d'une matrice M1, les i2 lignes suivantes sont les lignes i1+1, …, i1+i2 d'une autre matrice M2 et ainsi de suite avec les matrices M3 à Mk. Généralement, pour des raisons de simplification, les différentes matrices d'évolution Mi sont choisies auto-similaires. Le mélange permet la croissance d'arbres non statistiquement auto-similaires.

Considérons par exemple la matrice obtenue par le mélange suivant : les lignes 1 à 4 sont issues de la matrice d'évolution limite des arbres binaires aléatoires croissants (Table 4F), les lignes 5 et 6 sont celles de la matrice des arbres binaires aléatoires de taille 30000 et d'âge 9 (table 4D), toutes les lignes suivantes sont celles de la matrice identité, qui est la matrice d'évolution des arbres binaires parfaits. Cette matrice est donnée à la table 4L.

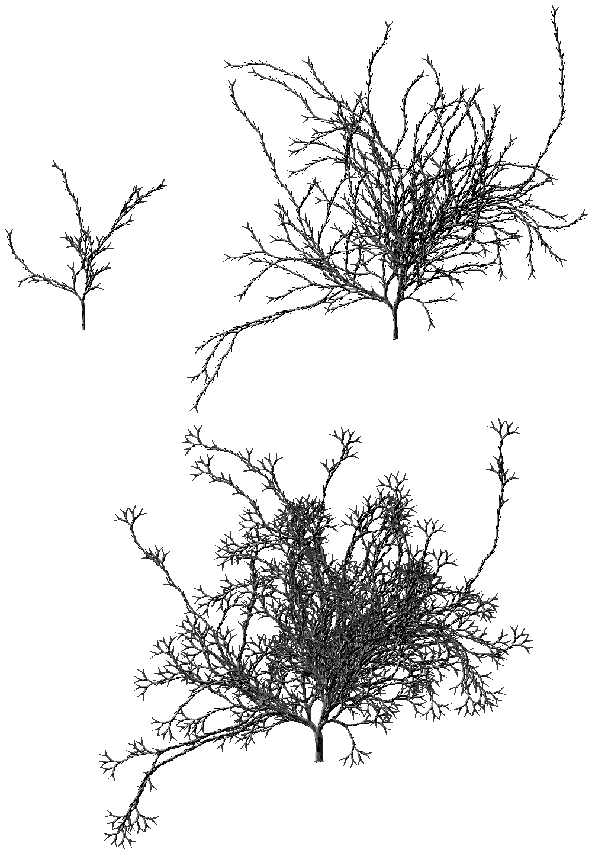
Photographies 4G: Evolution d'un arbre issu d'une matrice construite par mélange de lignes (Ages 5, 7 et 10)

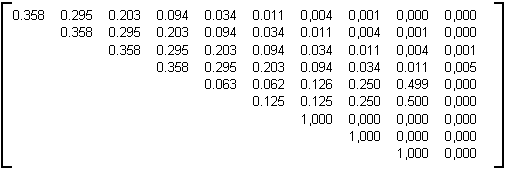
Image028.gif (4185 octets)

Table 4L : matrice issue d'un mélange de lignes.

La croissance d'un arbre pilotée par cette matrice d'évolution présentera trois étapes bien différenciées (Photographie 4G): Les quatre premières générations donneront un arbre bien équilibré présentant les caractéristiques d'un arbre binaire aléatoire croissant (Age 5), puis les deux générations suivantes feront pousser de longs segments décharnés comme sur un arbre binaire aléatoire (Age 7), enfin les générations suivantes feront apparaître de petits arbres parfaits (Age 10) permettant d'obtenir un effet de bouquet aux extrémités des segments d'ordre 5 et 6.

On constate ainsi que l'outil matrice d'évolution permet un fort contrôle de la forme d'un arbre à chacune des étapes de la croissance.

4.7 Liens entre nombres de Strahler et ordres d'évolution

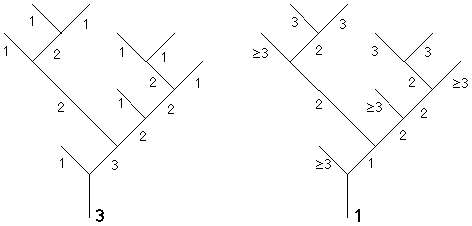
Image029.gif (3048 octets)

Figure 4J: Ordres de Strahler et ordres d'évolution extraits sur un même arbre

Intuitivement il est évident qu'il existe des corrélations importantes entre les notions d'ordre de Strahler et d'ordre d'évolution. La figure 4J décrit les ordres de Strahler et d'évolution extraits sur un même arbre. Nous allons établir précisément la loi de correspondance entre les deux notions d'ordres ainsi que la relation entre matrice de ramification et sous-matrice d'évolution extraites d'un même arbre.

Théorème

Soit un arbre binaire T quelconque donné dont chaque nœud n est muni d'un ordre de ramification et d'un ordre d'évolution :

(1) Age(T) = Ordre_Strahler(T)

(2) n étant un nœud interne ou une feuille dont le nœud frère est une feuille (fourche):

Ordre_Evolution(n) + Ordre_Strahler(n) = Age(T) + 1,

(3) n étant une feuille dont le frère n'est pas une feuille :

Ordre_Evolution(n) = Age(T)

Démonstration

Démontrons l'égalité (1) par récurrence. On note Ti l'arbre obtenu après i-1 générations à partir de T1 réduit à une seule arête.

- Le résultat est évident pour l'arbre T1 : Age(T1) = Ordre_Strahler(T1) = 1.

- Supposons le résultat vrai pour l'arbre Ti : Age(Ti) = Ordre_Strahler(Ti) = i.

- Réalisons une génération de plus.

Dans l'arbre Ti+1, les segments d'ordre d'évolution j, 1 £ j £ i, s'achèvent par une fourche (j+1,j+1). Ainsi, si l'on passe aux ordres de Strahler, les fourches terminales (i+1,i+1) constituées de feuilles de Ti+1 sont étiquetées (1,1). Par suite, les arêtes étiquetées i des segments d'ordre d'évolution i créés au cours de la génération i sont étiquetés 2 (En effet les autres feuilles issues de ces segments et créées au cours de la génération i sont d'ordre de Strahler 1 et ne modifient pas les ordres de Strahler (=2) des arêtes des segments d'ordre d'évolution i). Par suite les arêtes des segments d'ordre d'évolution i-1 qui s'achèvent dans Ti et Ti+1 par des fourches de biordre d'évolution (i,i) et donc de biordre de Strahler (2,2) seront d'ordre de Strahler 3. Ainsi de suite, les ordres de Strahler des arêtes des segments de Ti+1 d'ordre d'évolution = i, sont toutes augmentées d'une unité. On a ainsi montré le (1).

Le (2) s'ensuit à l'évidence, également par récurrence (dont l'initialisation est évidente), puisque quand j passe de i à i+1, Ordre_Strahler(Tj) et Ordre_Strahler(n) augmentent simultanément d'une unité pour tous les nœuds internes n de Ti également internes de Ti+1. Le résultat étant évident pour les nœuds de Ti+1 dans des segments d'ordre d'évolution i (i = 1 + Ordre_Strahler(Ti+1) - 2) et pour les nœuds feuilles des fourches de Ti+1 (i+1 = 1 + Ordre_Strahler(Ti+1) -1).

Le (3) est alors évident par la définition de la méthode de génération

Corollaire : Liens entre la matrice de ramification et la sous-matrice d'évolution extraites d'un arbre donné

On obtient la sous-matrice d'évolution d'ordre age(T)-1 extraite d'un arbre binaire T quelconque en fonction de sa matrice de ramification extraite (et réciproquement) en inversant l'ordre des lignes de la matrice source et sur chaque ligne en inversant l'ordre des probabilités d'apparition (Figure 4K).

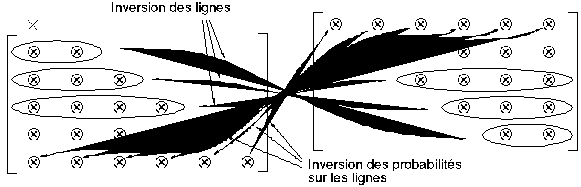
Image030.gif (5357 octets)

Figure 4K: Correspondance entre matrice de ramification et sous-matrice d'évolution

Démonstration

Conséquence du théorème précédent (formules (1) et (2)).

4.8 Conclusion

La dimension supplémentaire apportée par les matrices d'évolution par rapport aux matrices de ramification est qu'elles permettent intrinsèquement la simulation de la croissance d'arborescences topologiques binaires. La modélisation de l'évolution s'effectue par la génération d'une suite discrète d'arbres. Par la paramétrisation des valeurs numériques contenues sur les lignes, il est possible de contrôler la forme adoptée par l'arbre topologique tout au long de sa croissance ainsi que la vitesse de croissance de la structure.

Ces matrices apportent aussi un outil autorisant l'analyse de la croissance d'arbres topologiques binaires issus de processus divers. Elles s'adaptent bien à l'étude des processus évolutifs mettant en œuvre une croissance par les bords.

La synthèse d'images d'arbres botaniques par des méthodes combinatoires peut maintenant s'effectuer en tenant compte du processus évolutif de manière à simuler la croissance des arbres au cours du temps.