Chapitre 5
Algorithmes de plongement automatique
de cartes planaires
5 Algorithmes de plongement automatique de cartes planaires
Comme nous le verrons dans cette partie, la modélisation et le dessin de reliefs va requérir l'écriture d'un algorithme de dessin de carte planaire par segments de droites liant, au moins en partie, le nombre de sommets dessinés et l'aire de la zone qui les contient. Les algorithmes de dessin automatique de cartes planaires proposés dans la littérature sont généralement implantables en temps linéaire du nombre de sommets et d'arêtes de la carte dessinée, ce qui est une condition importante d'utilisation, au prix toutefois de manipulations assez compliquées sur la structure de données.
Nous présentons dans ce chapitre certains des algorithmes classiques de plongement automatique de cartes planaires. La présentation suit un parallèle avec celle du chapitre 2 sur le dessin d'arbres binaires. Ce chapitre s'achèvera par un parallèle fait entre ces deux types de dessins, parallèle fructueux puisque le dessin d'arbres est beaucoup plus avancé que celui des cartes planaires, conduisant à de nouvelles idées de plongement automatique de cartes planaires (travaux en cours). Ce chapitre servira également d'introduction au chapitre suivant qui propose un nouvel algorithme de plongement d'une carte planaire munie d'un arbre binaire recouvrant, algorithme qui sert de base à une nouvelle technique de synthèse d'images de reliefs montagneux (cf chapitre 6).
5.1 Définitions et théorème
Carte planaire simple
Figure 5A : Carte planaire non simple
Une carte planaire est dite simple si elle ne possède ni boucle (arête dont les sommets sont identiques) ni arête multiple (arêtes joignant le même couple de sommets) (Figure 5A).
Ensemble d'articulation et cartes 2 et 3-connexes
Un ensemble d'articulation est un ensemble de sommets d'une carte dont le retrait déconnecte la carte. Si cet ensemble est réduit à un (respectivement deux) sommet(s), il est appelé sommet (respectivement paire) d'articulation.
Une carte est dite 2-connexe si elle n'a pas de point d'articulation. Une carte 2-connexe qui n'a pas de paire d'articulation sera dite 3-connexe.
Nous considérerons dans la suite le problème du dessin de cartes planaires 2-connexes. Le cas des cartes planaires connexes, mais non 2-connexes, s'y ramène facilement.
Cartes planaires triangulaires et quasi-triangulaires
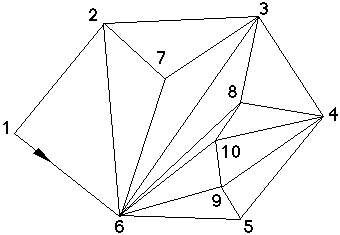
Figure 5B : Carte planaire pointée quasi-triangulaire
On appelle carte planaire pointée triangulaire une carte planaire pointée simple dont toutes les faces sont de degré trois (sont des triangles). Une carte planaire pointée simple est dite quasi-triangulaire si toutes ses faces sauf éventuellement sa face extérieure sont de degré trois (Figure 5B).
Dessin "convexe" dans le plan
Une carte planaire sera dite dessinée dans le plan, si l'on a déterminé pour chacun de ses sommets un couple de coordonnées dans un repère donné, de façon que les arêtes de la carte soient dessinées par segments de droite et ne se coupent pas en dehors de leurs sommets extrémités.
Le dessin de cette carte sera dit convexe, si de plus, sa face extérieure est un polygone convexe.
Théorème
Les paires d'articulation d'une carte planaire 2-connexe quasi-triangulaire sont les ensembles de sommets {s1,s2} incidents à la face extérieure, tels que {s1,s2} soit une arête de la carte sans être une arête bordant la face extérieure.
Démonstration : cf [La84]
5.2 Algorithme de Fary-Laumond pour le dessin de cartes planaires quasi-triangulaires
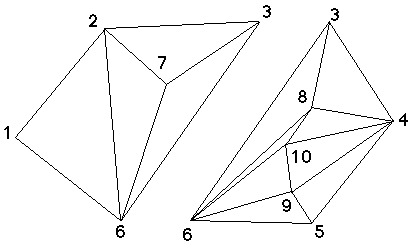
Figure 5C : Décomposition de la carte de la figure 5B selon la paire d'articulation (3,6) : Si le polygone (1,2,3,4,5,6) est convexe, il en est encore de même pour les deux polygones (1,2,3,6) et (3,4,5,6)
Laumond a proposé un algorithme automatique de dessin convexe de cartes planaires quasi-triangulaires 2-connexes ou 3-connexes [La84]. Il se base sur les deux propositions suivantes :
Proposition 1
La décomposition d'une carte planaire 2-connexe dessinée de façon convexe dans le plan, suivant l'arête associée à une paire d'articulation, crée deux cartes planaires 2-connexes ou 3-connexes dessinées de façon convexe.
Preuve : Evident, cf figure 5C.
Proposition 2
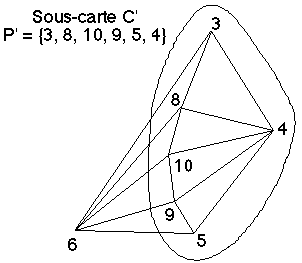
Figure 5D : Suppression du sommet 6 dans la carte de la partie droite de la figure 5C
Soit C une carte planaire 3-connexe et s un sommet de sa face extérieure. Soit C' la carte 2-connexe ou 3-connexe obtenue en supprimant le sommet s et les arêtes issues de s. Pour dessiner C de façon convexe, sa face extérieure étant un polygone convexe P donné, il suffit de dessiner C' de façon convexe, sa face extérieure étant le polygone convexe P' construit à partir de P en ôtant de P son secteur angulaire de sommet s et en lui substituant la suite ordonnée des sommets adjacents à s, positionnée de manière convexe à l'intérieur de ce secteur angulaire (Figure 5D).
Preuve : Evident
Idée de l'algorithme
L'algorithme de Laumond se base sur la stratégie de décomposition topologique suivante utilisant les deux propositions précédentes (il n'est applicable que sur les cartes planaires quasi-triangulaires 2-connexes ou 3-connexes) :
Soit C la carte 2-connexe ou 3-connexe que l'on cherche à dessiner de façon convexe, sa face extérieure est fixée a priori comme étant un polygone convexe P donné.
- Si C a trois sommets, C est un triangle et son dessin convexe est celui de P.
- Si C n'est pas réduite à un triangle et n'est pas 3-connexe, le dessin de C est ramené récursivement au dessin convexe des deux nouvelles cartes obtenues à partir de C par décomposition suivant l'une des paires d'articulation présente dans C (proposition 1 et théorème du paragraphe 5.1).
- Si C est 3-connexe alors le dessin convexe de C est ramené au dessin convexe de la carte C' par suppression de l'un des sommets de sa face extérieure (proposition 2).
Exemple
L'exemple décrit par la figure 5E montre les différentes étapes de la décomposition. Le choix de la paire d'articulation provoquant le partage de la carte en deux sous-cartes ou du sommet supprimé est arbitraire.
Cette décomposition ne décrit pas la manière avec laquelle les positions des sommets sont choisies lors du dessin de la liste d'adjacence d'un sommet supprimé. Toute méthode assurant la convexité du bord construit est acceptable. Il est toutefois souhaitable que le placement soit assez régulier.
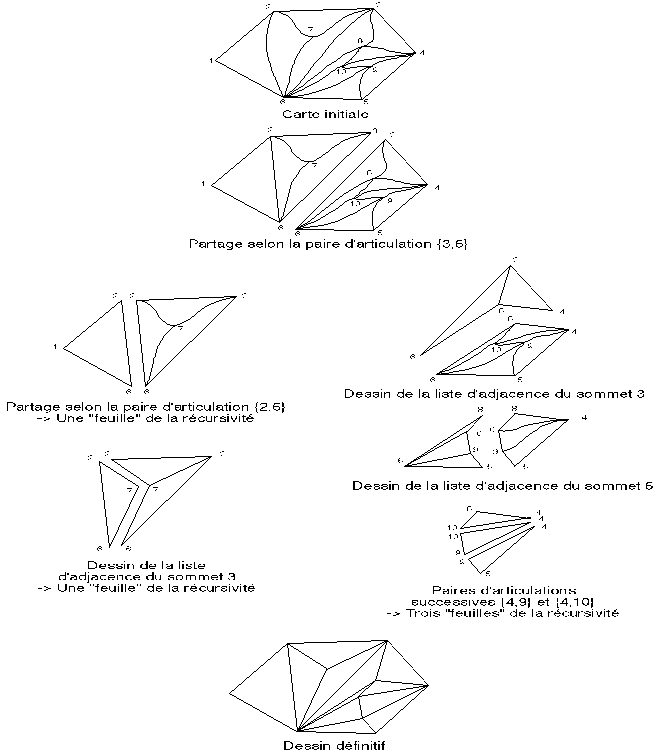
Figure 5E: Décomposition et dessin d'une carte quasi-triangulaire par l'algorithme de Laumond. Dans cette figure, les arêtes droites sont définitivement positionnées et les arêtes courbes ne le sont pas encore (un ou deux de leurs sommets extrémités ne sont pas encore fixés).
Algorithme
L'algorithme de dessin est essentiellement composé de la procédure récursive DESSIN. Le programme appelant devra dessiner le polygone convexe représentant le bord de la carte avant de lancer cette procédure.
Procedure DESSIN (C : carte)
sommet : S
paire d'articulation : P
carte : C1, C2, C'
début
si C n'est pas réduite à un triangle alors
si ilexiste une paire d'articulation P dans C alors
dessiner la paire d'articulation P
Partager C en deux sous-cartes C1 et C2
DESSIN(C1)
DESSIN(C2)
sinon
choisir un sommet S de la face extérieure de C
Positionner et dessiner la liste d'adjacence de S dans C
Construire C' par suppression de S dans C
DESSIN(C')
fin_si
fin_si
fin_procedure
L'implantation de cet algorithme en temps linéaire du nombre de sommets de la carte à dessiner demande un certain nombre de précautions. En particulier, la recherche des paires d'articulation, si elle est mal effectuée, peut conduire à l'obtention d'un algorithme en n2. En effet, une méthode simple de recherche des paires d'articulation dans une carte C consiste à parcourir les nœuds s du bord extérieur de C et pour chaque s, à parcourir la liste de ses sommets successeurs, à l'exception du suivant et du précédent sur le bord extérieur de C, de manière à trouver les sommets se trouvant sur le bord de C.
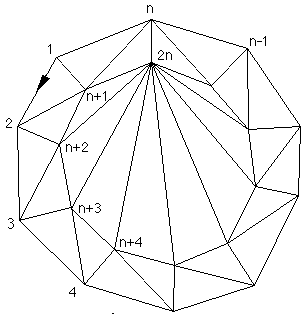
Figure 5F : Exemple
Cette méthode permet de déterminer très facilement les paires d'articulation, mais dans le cadre d'une implantation de la décomposition de Laumond, elle n'est pas linéaire du nombre n de sommets de la carte. En effet, si l'on considère la carte à 2n sommets de la figure 5F, la recherche d'une paire d'articulation n'aboutit pas après 2n tests (un pour chacun des deux successeurs des n sommets du bord extérieur). On supprime alors le sommet 1, pour obtenir une nouvelle carte à 2n-1 sommets dans laquelle on doit de nouveau chercher les paires d'articulation, ce qui demande 2n-1 tests et n'aboutit pas. Se processus de suppression d'un nœud et de recherche des paires d'articulation de la carte ainsi obtenue se reproduit jusqu'à la suppression du sommet n (suppression dans l'ordre de numérotation des nœuds sur le bord extérieur de la carte de la figure 5F). Le nombre de tests ainsi effectués est de l'ordre du carré de n.
Afin d'éviter ce problème, il faut implanter l'algorithme de façon à ce que la liste des successeurs de chaque sommet soit testée une fois et une seule au cours de la décomposition. On s'assure ainsi de la linéarité en fonction du nombre d'arêtes et donc du nombre de sommets.
L'idée de l'algorithme consiste à ajouter un champ "visité" de type booléen à la structure de données de stockage d'un nœud. Tous ces champs seront initialisés à faux au début de l'algorit
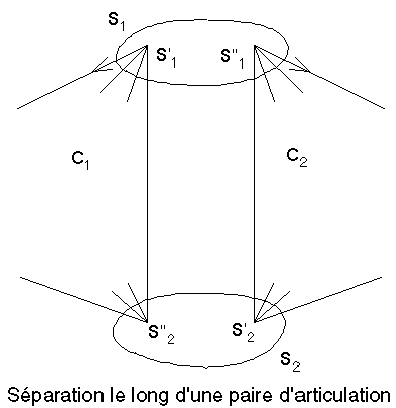
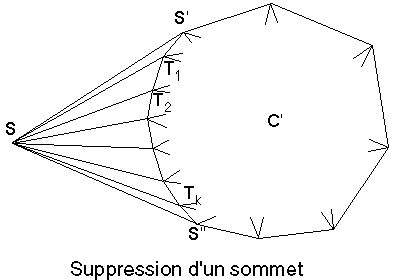
hme.Figure 5G : Opérations de décomposition topologique
Pour la carte C de départ, on commence la recherche à partir du sommet pointé 1 jusqu'à trouver un sommet s1 de la face extérieure qui avec un de ses successeurs s2 forme une paire d'articulation. Les sommets testés à partir de 1 jusqu'au prédécesseur de s1 sur ce bord et pour lesquels la recherche a échoué ont leurs champs "visité" mis à vrai. On partage la carte C en deux cartes C1 et C2 en dédoublant les sommets s1 et s2 respectivement en s'1, s"1 et s'2, s"2 (Figure 5G haut). Le champ visité du sommet s"1 est également mis à vrai. On relance la procédure récursive DESSIN sur C1 et C2. On constate alors que pour C2, la recherche d'une paire d'articulation se fait à partir de s'2 mais devra s'arrêter au sommet 1, c'est à dire au premier sommet que l'on rencontre et qui a déjà été visité. En effet, les sommets du bord de C2 sont également du bord de C et toute paire d'articulation de C2 est paire d'articulation de C. On ne peut donc pas trouver une telle paire dans C2, incluant un sommet précédemment visité et pour lequel la recherche a échoué. Cette remarque s'applique à l'évidence récursivement à toutes les cartes issues de l'opération de séparation le long d'une paire d'articulation.
Lorsque la recherche d'une paire d'articulation pour une carte C échoue, c'est à dire que tous les sommets du bord extérieur de C ont été marqués, la carte C est 3-connexe. L'opération appliquée est la suppression d'un sommet de la face extérieure de C, ce qui revient à définir une nouvelle carte C' (Figure 5G bas). Le bord extérieur de C' est constitué du bord de C auquel on a retranché s, remplacé par les nouveaux sommets T1, ..., Tk. L'appel de la procédure DESSIN sur C' conduit à la recherche d'une paire d'articulation. Si cette paire existe, l'un de ses deux sommets est nécessairement l'un des nouveaux Ti, sinon cette paire aurait aussi été paire de C, et aurait donc déjà été détectée. Ainsi pour trouver toutes les paires d'articulation de C', il suffit de visiter les sommets T1, ..., Tk.
On voit donc que la règle générale d'obtention des paires d'articulations de la carte courante C, est de tester les successeurs des sommets de sa face extérieure qui n'ont pas encore été visités. On est ainsi certain de ne tester qu'une seule fois chaque arête.
Conclusion
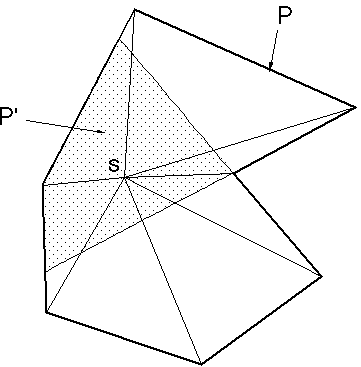
Figure 5H : Replacement barycentrique
La décomposition de Laumond fournit des dessins de cartes planaires dont on ne peut pas contrôler les caractéristiques géométriques internes. On constate par exemple dans certains cas particuliers des accumulations de sommets sur de petites surfaces, rendant les dessins assez peu esthétiques. Pour améliorer le placement des points, Laumond définit une méthode barycentrique de déplacement des sommets du graphe dessiné. Chaque sommet s est ainsi replacé au centre du polygone convexe maximum P' inscrit dans le polygone P union des facettes incidentes à s (prise en compte des contraintes de planarité liées à la non convexité éventuelle de P) (Figure 5H).
5.3 Notion de dessin esthétique d'une carte
Si l'algorithme de Laumond est simple, il n'intègre que peu de contraintes esthétiques (uniquement le dessin des arêtes par segments de droite). Comme on le constate dans les dessins obtenus (cf [La84] et Figure 5N, paragraphe 5.4), cette contrainte est aussi insuffisante pour le dessin automatique de cartes planaires que la contrainte analogue pour le dessin automatique d'arbres (Chapitre 2). On est donc amené à poser le problème d'un dessin "agréable" d'une carte planaire et donc à définir la notion d'esthétique dans le dessin d'une carte
Une contrainte esthétique de dessin de cartes planaires quelconques souvent rencontrée est la suivante :
Contrainte 1
Toutes les arêtes doivent être dessinées par segments de droite sans autre point d'intersection que leurs extrémités.
Figure 5I : Amélioration du dessin convexe (à gauche) par le dessin totalement convexe (contrainte esthétique 2, à droite)
Cette simple règle a été mise en œuvre au paragraphe précédent dans le cas particulier du dessin de cartes planaires quasi-triangulaires mais elle est applicable à toutes les cartes planaires. Cette contrainte fournit généralement d'assez bons résultats.
Une autre contrainte esthétique relativement naturelle fournissant aussi de bons résultats (Figure 5I) et permettant d'obtenir un dessin appelé par définition dessin totalement convexe est :
Contrainte 2
Les arêtes de la carte doivent être représentées par des segments de droites et la frontière de chacune des faces doit être dessinée selon un polygone convexe.
Il faut remarquer que si toute carte planaire simple peut être dessinée en respectant la règle esthétique 1, il n'en est pas de même pour la contrainte esthétique 2. On démontre toutefois que toute carte planaire simple 3-connexe peut être dessinée en respectant la contrainte esthétique 2 (voir ci-après Lemme de Thomassen).
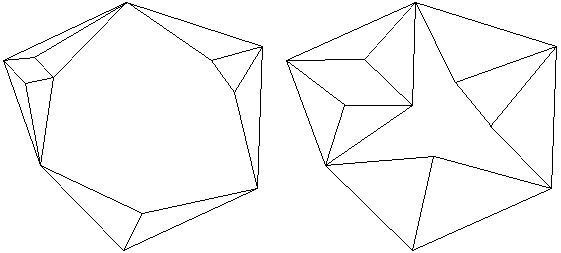
Figure 5J : Amélioration du dessin totalement convexe par application de la contrainte esthétique 3.
Remarque
Le dessin présenté dans l'exemple de la figure 5J à gauche montre que le respect de la contrainte esthétique 2 ne fournit pas nécessairement des résultats très esthétiques (Comparer à la partie droite de la Figure 5J qui semble "plus lisible").
Une troisième contrainte esthétique issue de cette remarque reprend le meilleur des 2 premières contraintes dans le sens où elle permet de bien mettre en vue les composantes 3-connexes d'une carte planaire quelconque qui seraient probablement peu lisibles car dessinées dans des régions exiguës si la contrainte 2 était strictement appliquée (Figure 5J gauche) :
Contrainte 3
- Les arêtes sont représentées par des segments de droite.
- Les frontières extérieures de toute les composantes 3-connexes présentes dans la carte doivent être représentées par des polygones convexes.
- Représenter aussi souvent que possible les faces par des polygones convexes.
Le paragraphe 5.4 suivant propose un algorithme dû à Chiba et al (cf [CO85]) de dessin automatique de cartes planaires satisfaisant la contrainte esthétique 2 de totale convexité. Une amélioration de cet algorithme pour la satisfaction de la contrainte esthétique 3 peut être également trouvée dans [CO85] et ne sera détaillée ici. Quelques définitions et résultats préliminaires sont nécessaires avant de présenter cet algorithme :
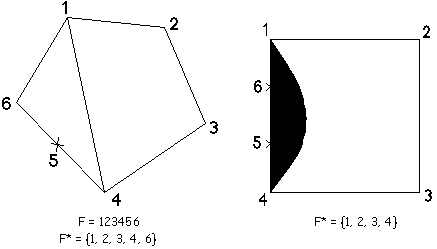
Figure 5K : Face
extérieure et dessin
Figure 5L : Dessin
polygonal convexe de cette face
polygonal convexe
Dessin polygonal convexe F* prolongeable non prolongeable
Définition
Soit F, la face extérieure de la carte pointée C, et soit F* un "dessin polygonal convexe" (on dira polygone convexe) de F. Remarquer que les sommets géométriques du polygone F* forment un sous-ensemble des sommets de F, et que chaque coté du polygone F* est un chemin qui fait partie de la frontière de F (Figure 5K). On appellera g-sommets les sommets de F qui sont des sommets géométriques de F*.
On dira F* prolongeable s'il existe un dessin totalement convexe de la carte C admettant F* pour frontière extérieure (Figure 5K et 5L).
L'idée intuitive sous-jacente au lemme de Thomassen ci-dessous est que si une carte planaire peut être dessinée de façon totalement convexe, alors ses paires d'articulation sont formées de sommets situés sur sa face extérieure (propriété généralisant celle admise dans les paragraphes précédents pour les cartes planaires quasi-triangulaires).
Lemme de Thomassen [Th80]
Soit C une carte planaire pointée, de face extérieure F et soit F* un dessin polygonal convexe de F à k cotés. On note P1, P2, .., Pk les chemins de F, correspondant aux k cotés successifs de F*. F* est prolongeable si et seulement si les trois conditions suivantes sont réalisées :
- Pour tout sommet V de C qui ne soit pas sur F et qui soit de degré au moins trois, il existe trois chemins ayant deux à deux pour seul point commun le sommet V, chacun joignant V à un sommet de F.
- Le graphe issu de C en supprimant tous les sommets de F (et les arêtes qui leur sont incidentes) n'a pas de composante connexe C telle que tous les sommets de F adjacents aux sommets de C soient sur un même chemin Pi. De plus une arête de C joint deux sommets de Pi si et seulement si elle appartient à Pi.
- Tout circuit de C qui n'a aucune arête en commun avec F possède au moins trois sommets de degré = 3 dans C.
Démonstration : cf [Th80] ou [Ar88].
Ce lemme possède deux corollaires importants (admis) de par leurs implications dans le dessin automatique de cartes planaires :
Corollaire 1 :
Si pour une carte planaire pointée C, il existe un dessin polygonal convexe F* prolongeable de sa face extérieure F, alors le polygone convexe obtenu en positionnant les sommets de F sur un cercle est également prolongeable.
On a ainsi dans cette situation toute liberté pour le placement des sommets de F.
Corollaire 2 :
Toute carte planaire pointée 3-connexe est dessinable de façon totalement convexe.
5.4 Algorithme de Chiba, Onoguchi et Nishizeki pour le dessin totalement convexe d'une carte planaire 2-connexe quelconque
Une résolution du problème lié à la contrainte esthétique 2 de dessin totalement convexe a été apportée par Chiba, Onoguchi et Nishizeki [CO85].
Idée de l'algorithme
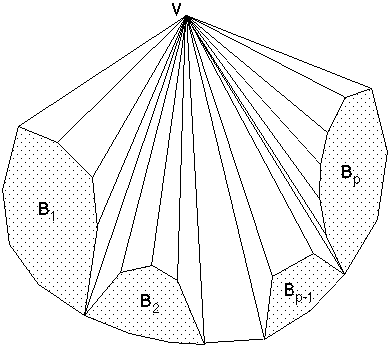
Figure 5M : Décomposition d'une carte par Chiba, Onoguchi et Nishizeki
La démonstration constructive (non donnée ici) du lemme de Thomassen conduit à la décomposition algorithmique suivante de la carte dont on réalise le dessin :
C étant une carte munie d'un dessin polygonal convexe F* de sa face extérieure F, on réduit le dessin de C à ceux de sous-cartes de C de la façon suivante (Figure 5M):
- Supprimer de C un g-sommet V quelconque, ainsi que toutes les arêtes issues de V.
- Décomposer la carte C' ainsi obtenue en les blocs B1, B2, ..., Bp, p = 1.
- Déterminer un polygone convexe Fi* de la face extérieur Fi de chaque Bi telle que (Bi, Fi, Fi*) satisfasse les conditions du lemme de Thomassen.
- Appliquer alors récursivement l'algorithme à chaque Bi muni de Fi* afin de déterminer la position des sommets qui ne sont pas sur Fi.
Algorithme
L'implantation de l'algorithme repose sur les deux procédures suivantes :
Procedure DESSIN_TOTALEMENT_CONVEXE (C, F, F*)
/* C est une carte planaire 2-connexe, F sa face extérieure,
F* un dessin polygonal convexe de F prolongeable */
sommet : V
carte : C'
début
/* Le dessin de C est réduit à celui de la carte C',
par suppression de tous les sommets de C
qui sont de degré 2 et qui ne sont pas sur F */
pour chaque sommet V de degré 2 non sur F faire
Remplacer V et les deux arêtes incidente de V
par une seule arête joignant les sommets
adjacents à V pour créer une nouvelle carte C' à partir de C
fin_pour
PROLONGEMENT(C', F, F*)
pour chaque sommet de degré 2 supprimé faire
Déterminer une position pour ce sommet
sur le segment de droite joignant
les deux sommets qui lui sont adjacents
fin_pour
fin_procedure
Procedure PROLONGEMENT(C,F,F*)
sommet : V
carte : C'
tableau de sommets : Vi
face extérieure : FI
dessin polygonale convexe : FI*
début
si C a au moins quatre sommets alors
/* Sinon un dessin totalement convexe est déjà obtenu */
Choisir arbitrairement un g-sommet V de F*
C' = C \ {V}
Diviser la carte C' en les blocs Bi (1=i=p), et déterminer p
Déterminer les sommets Vi
/* p est égal à 1 + le nombre de sommets d'articulation de C'.
V1 et Vp+1 sont les deux sommets adjacents à V sur F. Vi,
2=i=p sont les sommets d'articulation de C' */
pour chaque bloc Bi faire
/* Détermination d'un polygone convexe FI* de la face extérieure FI de Bi
en déterminant les positions des sommets de FI\F puisque ceux de FI9F
sont déjà placés */
Placer les sommets de FB\F à l'intérieur du triangle ViVVi+1
de telle façon que les sommets adjacents à V soient
des g-sommets du polygone FI* et que les autres
soient sur les segments de droite de FI
PROLONGEMENT(Bi,FI,FI*)
fin_pour
fin_si
fin_procedure
Exemple
La figure 5N suivante décrit les dessins obtenus par les algorithmes de Laumond et Chiba sur une même carte planaire quasi-triangulaire.
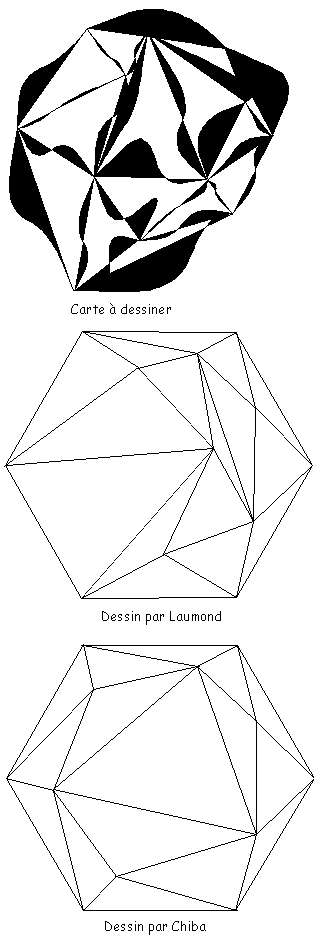
Figure 5N : Exemples de dessins
Conclusion
Cet algorithme permet d'obtenir un dessin totalement convexe de toute carte planaire 2-connexe dont la face extérieure F possède un polygone convexe F* prolongeable. En reprenant une partie des implantations proposées pour l'algorithme de Fary-Laumond, on montre facilement que cet algorithme donne un dessin convexe de la carte en temps linéaire du nombre de ses sommets.
Il n'en reste pas moins que dans certains cas particuliers le dessin reste inesthétique par accumulation de sommets dans certaines zones. Dans [CO85], un second algorithme est proposé améliorant les résultats par satisfaction de la contrainte esthétique 3 (Non détaillé ici).
Un problème ouvert reste dans ce contexte l'écriture d'un algorithme vérifiant des contraintes physiques comme par exemple :
- une densité de sommets relativement uniforme dans toute la carte,
- une fluctuation des longueurs d'arêtes la moins grande possible,
ou bien encore esthétiques comme par exemple :
- conservation des symétries caractéristiques d'une carte,
- dessin identique ou homothétique des motifs se répétant à différents endroits d'une même carte.
Ces problèmes sont exprimés de la façon suivante à la fin de [C085] :
"It remains open to improve the drawing algorithm so that it gives more favorable drawings with respect to another criterion, for example in a way that the areas of faces are balanced."
5.5 Quelques idées sur un algorithme de dessin de cartes planaires respectant des contraintes physiques
Dans [Ar88] et [AJ92b], sont proposés un certain nombre d'idées qui pourraient conduire à un algorithme de dessin automatique de cartes planaires avec respect de contraintes physiques ou esthétiques telles que celles citées à la fin du paragraphe précédent.
Analysons l'enchaînement des algorithmes du chapitre 2 (cf fin du chapitre 2), débutant par un algorithme qui dessine sans respecter aucune contrainte esthétique pour aboutir au quatrième algorithme qui respecte des contraintes esthétiques relativement fines: Ce qui différentie le quatrième algorithme de dessin en postordre de Reingold et Tilford des trois précédents est que le dessin d'un sous arbre est fait a priori, sans aucune influence des sommets de l'arbre extérieurs à ce sous-arbre. Ceci explique que deux sous-arbres identiques soient dessinés identiquement et que les symétries soient préservées. Au contraire dans les trois autres algorithmes, et en particulier dans le troisième de Wetherell et Shannon, ce sont les sommets qui sont positionnés (et non les sous-arbres), et le positionnement d'un sommet dépend de la future place libre sur son niveau, donc des sommets situés a sa gauche (ce qui se traduit dans l'algorithme par la mise à jour d'un tableau "place suivante"). Le choix a priori d'une marge gauche fixe (dans le dessin) ne permet pas de respecter les symétries éventuelles dans le dessin et influe sur le positionnement des sommets.
Si on transpose cette analyse au cas des cartes planaires, on constate que le parallèle est complet entre le dessin des arbres binaires et le dessin des cartes planaires :
Dans les deux algorithmes des paragraphes précédents le positionnement des points sur la frontière extérieure de la carte est fait au départ de l'algorithme, selon un polygone convexe arbitraire: Ce polygone convexe joue dans le cas du dessin de cartes planaires le rôle que la marge gauche joue dans le dessin des arbres binaires. Une fois ce polygone fixé, le choix pour positionner les autres sommets devient pratiquement nul; en effet la nécessité de garder la convexité impose alors de positionner les sommets restant à l'intérieur des secteurs angulaires de sommets dessinés dans un appel récursif précédent (se référer aux algorithmes). Dès lors, le positionnement des sommets extérieurs est essentiel car il contient en lui le dessin final de la carte! Or n'ayant aucune information nous permettant de gérer ce lien entre polygone externe de départ et dessin final de la carte, les algorithmes proposés choisissent arbitrairement ce polygone de départ, et le plus souvent sous forme d'un polygone régulier, se reporter aux résultats des chapitres précédents: ceci explique les dessins déséquilibrés que l'on obtient alors.
Une autre raison de l'impossibilité de tenir compte dans les algorithmes précédents de contraintes plus fines est "l'esprit local" qui préside à la conception de ces algorithmes (analogue du traitement en préordre dans le cas des arbres). A aucun moment, en effet, les paramètres globaux de la carte ne sont pris en compte dans le positionnement des points: Un tel paramètre de nature globale est par exemple le nombre de points à placer dans une partie donnée de la carte: Dans la figure 5O, par exemple, les deux paires d'articulation séparent la carte initiale en trois parties dont la partie centrale contient beaucoup plus de sommets internes que les deux autres (qui n'en contiennent pas). La connaissance de ce fait impose lors du choix du polygone externe, de ne pas positionner les sommets externes sur un polygone régulier comme dans la partie gauche de la figure mais plutôt selon la répartition de la partie droite de la figure 5O. Là encore le choix arbitraire du polygone fait dans les algorithmes actuellement existants a toute chance d'aboutir à un dessin mal équilibré.
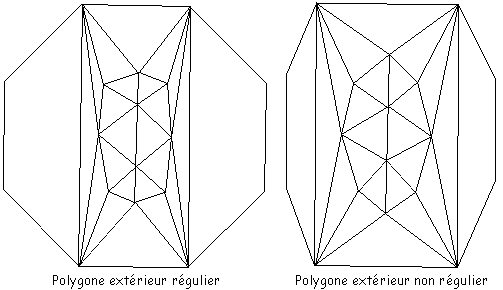
Figure 5O : Influence de la forme du polygone extérieur sur le dessin
Pour pouvoir tenir compte des différences entre les trois sous-cartes déterminées par les deux paires d'articulation dans la figure 5O, il aurait fallu les dessiner (ou pour le moins connaître certaines de leurs caractéristiques comme le nombre de leurs sommets) avant de les positionner les unes par rapport aux autres et en particulier avant de décider arbitrairement la position de leurs sommets extérieurs. C'est le contraire qui est fait dans les deux algorithmes de Laumond et Chiba. Par contre, l'idée de dessiner les trois cartes avant de les recoller est en fait l'idée de traitement en postordre utilisée par Reingold et Tilford dans le quatrième algorithme du chapitre 2: Pour dessiner un sous-arbre, ils dessinent d'abord le sous-arbre gauche de la racine, puis le sous-arbre droit, ces deux sous-arbres devenus "rigides" sont alors positionnés l'un par rapport à l'autre et la racine est alors centrée par rapport à ses deux fils, racines de ces deux sous-arbres. De même une première solution à notre problème serait d'avoir une stratégie de décomposition d'une carte en sous-cartes, de dessiner ces sous-cartes, de les considérer si possible (en fait ce n'est pas si simple) comme rigides, de les positionner ensuite les unes par rapport aux autres (c'est à ce niveau du positionnement qu'il est alors possible de tenir compte de contraintes comme la densité de sommets) de façon à construire récursivement la carte de départ. On voit que dans cet algorithme, ce qui est dessiné en dernier, c'est la frontière extérieure! Elle est reconstruite à partir des frontières extérieures des sous-cartes rigides et de leur positionnement relatif. A noter qu'une telle stratégie de "traitement en postordre" permet d'introduire une vision "globale" de la carte que l'on dessine par opposition à la vision locale que l'on avait de la carte dans les précédents algorithmes (par exemple en positionnant les listes de successeurs du sommet ôté, on n'avait pour seule information que le nombre de ces successeurs mais en aucun cas "l'aspect" de la carte au delà de cette liste de successeurs): En effet en repositionnant des sous-cartes que l'on a déjà dessinées, on connaît (puisqu'on vient de les dessiner) toutes leurs caractéristiques comme par exemple le nombre de leurs sommets. Ceci permet en les positionnant les unes par rapport aux autres, de donner à chacune, par exemple, une place proportionnelle au nombre de ses sommets. C'est ce que l'on peut appeler avoir une "vision globale" de la carte que l'on dessine par rapport à une "vision locale" qui positionne des points sans connaître leur contexte. C'est aussi une autre différence entre ce nouvel algorithme et ceux des paragraphes précédents: Dans les algorithmes précédents, ce sont des points que l'on positionne, positionnement fortement influencé par ceux des frontières extérieures successives déjà positionnées, alors que l'on se propose de positionner des cartes rigides (dans un sens à préciser).
Cette stratégie laisse supposer d'importants problèmes sur deux points particuliers :
- contraintes géométriques (les contraintes géométriques de placement de deux sous-cartes l'une par rapport à l'autre sont importantes et imposent de façon quasiment obligatoire la convexité de leurs bords extérieurs),
- linéarité de l'algorithme (d'une manière encore plus sévère que pour le dessin d'arbres, la conservation de la linéarité de l'algorithme est un problème).
5.6 Conclusion
Les méthodes proposées dans ce chapitre, sauf la dernière, imposent le placement a priori des sommets de la face extérieure de la carte à dessiner (généralement sur des polygones réguliers) sans connaissance de l'intérieur de la carte. Cette contrainte est très forte, elle entraîne souvent des problèmes dans la répartition des nœuds à l'intérieure de la carte dessinée (trop forte densité sur certaines zones). Les algorithmes intuitifs qui permettraient de résoudre le problème du dessin de cartes planaires respectant des contraintes physiques de cette catégorie se heurtent à de graves problèmes de complexité et de linéarité.
Au chapitre 6 suivant, on propose un algorithme linéaire de plongement automatique qui apporte une solution à ce problème dans le cas d'une carte planaire quasi-triangulaire possédant un arbre binaire recouvrant. Ce type de carte est tout particulièrement adapté à la modélisation d'un relief montagneux (modélisé par la carte planaire) drainé par un réseau fluvial (modélisé par l'arbre binaire recouvrant). Avoir un algorithme qui gère la densité de sommets en fonction de la surface est essentielle dans ce cadre car comme on le verra au chapitre suivant, le dessin de cartes dont le nombre de nœuds peut être supérieur à plusieurs centaines est susceptible d'avoir à être réalisé dans la modélisation d'un bassin fluvial. Ceci implique d'obtenir une répartition harmonieuse des sommets pour réaliser des images de synthèse avec un bon rendu.