Chapitre 6
Plongement de cartes planaires
et synthèse d'images de bassins fluviaux montagneux
6 Plongement de cartes planaires
et synthèse d'images de bassins fluviaux montagneux6.1 Introduction
Dans les chapitres précédents, nous avons vu comment utiliser des arborescences binaires topologiques pour modéliser des arbres botaniques. L'analogie était alors tout à fait évidente. Le même type de démarche est possible en ce qui concerne la modélisation et le dessin de reliefs. La structure topologique binaire est alors le support du réseau fluvial sous-jacent à toute montagne ou chaîne de montagnes. Nous effectuons ici un "retour aux sources" car l'analyse effectuée par Horton et Strahler en hydrogéologie ([Ho45], [St52]) avait pour but de mettre en valeur un certain nombre de caractéristiques morphologiques des réseaux fluviaux (importance relative des rivières les composant : largeur, débit, étude de l'importance de la ramification du réseau binaire).
La démarche adoptée dans ce chapitre entre dans le cadre des méthodes statiques générant un relief à partir d'un modèle permettant de simuler les conséquences de l'érosion (cf paragraphe 1.3.3.1). La modélisation se décompose classiquement en deux parties séparant clairement les aspects topologiques et géométriques dans la conception du bassin fluvial et du relief correspondant.
La première partie, topologique, est constituée des étapes suivantes :
- Construction d'une arborescence binaire topologique à partir d'une matrice de ramification ou d'une matrice d'évolution (Paragraphe 6.2.1 et chapitres 3 et 4), nous permettant d'utiliser ainsi des ordres combinatoires entiers pour caractériser l'importance des différentes composantes de l'arbre binaire sous-jacent au réseau fluvial.
- Construction d'une carte topologique planaire quasi-triangulaire admettant cette arborescence binaire comme arborescence recouvrante (Paragraphe 6.2.2).
- Construction d'une carte planaire quasi-triangulaire raffinant la précédente par l'ajout de lignes de crêtes (Paragraphe 6.2.4).
- Cette modélisation est-elle suffisante au niveau topologique? Quelles opérations est-il possible d'effectuer pour l'améliorer (Paragraphe 6.2.5)?
La seconde partie, géométrique, est constituée des deux étapes :
- Conception d'un algorithme de plongement dans le plan de la carte planaire quasi-triangulaire dessinée par segments de droites en respectant des contraintes liant la surface occupée par une partie de la carte et l'importance du réseau fluvial (arborescence recouvrante) occupant cette surface (Paragraphe 6.3.2).
- Conception d'un algorithme de "remontée" des nœuds de la carte en une surface (relief) en respectant des contraintes issues de la géomorphologie de manière à créer un relief compatible avec le réseau fluvial (Paragraphe 6.3.4).
Il reste enfin à définir des méthodes permettant le dessin photoréaliste du relief modélisé en autorisant par exemple le dessin des montagnes avec leurs fleuves ou bien encore avec une végétation conçue au moyen des algorithmes qui ont été décrits dans les chapitres 3, 4 et 7.
Le premier point topologique a déjà été traité dans les chapitres 3 et 4. Les autres problèmes topologiques ainsi que les aspects purement géométriques seront en revanche abordés successivement dans ce chapitre. Enfin la dernière question concernant le dessin sera traitée dans le chapitre 8 qui aborde plus particulièrement les problèmes de dessin et de rendu réaliste des reliefs.
Ces travaux se distinguent des précédents dans leurs aspects topologiques :
- L'algorithme de construction automatique d'une carte planaire quasi-triangulaire par segments de droite admettant une arborescence planaire donnée comme arborescence recouvrante est nouveau.
- Le problème du dessin d'arborescences planaires et de cartes planaires respectant des contraintes de densité de points est reconnu comme difficile. Nous avons présenté certains de ces travaux, Wetherell, Shannon [WS79], Reingold, Tilford [RT81], Laumond [La84], Chiba, Onoguchi, Nishizeki [CO85], de Fraissex, Rosenstiehl [FR83,84], et analysé leurs caractéristiques comparées pour les arbres planaires et les cartes planaires aux chapitres 2 et 5. Nous proposons ici dans le cas d'une carte planaire quasi-triangulaire munie d'une arborescence binaire recouvrante, un nouvel algorithme, particulièrement bien adapté au problème infographique posé et permettant de respecter de tels types de contraintes.
Enfin, une autre caractéristique de ce travail est de réaliser une grande unité dans les algorithmes de synthèse de paysages naturels : ce sont en effet les mêmes algorithmes qui sont utilisés dans les photographies présentées pour construire l'arborescence sous-jacente au bassin fluvial et aux arbres botaniques portés par le bassin fluvial.
6.2 Définition et algorithme de construction d'une carte topologique planaire quasi-triangulaire sous-jacente à un bassin fluvial
6.2.1 Définition et construction d'un arbre binaire sous-jacent à un réseau fluvial
Un arbre binaire peut être associé à tout réseau fluvial (si on omet îles et points de jonction triple ou multiple) en oubliant sa géométrie et en ne gardant que sa topologie (avec les notions de droite et de gauche naturellement liées au fait que ce réseau fluvial est dessiné sur une surface).
L'arbre binaire sous-jacent au relief modélisé est considéré comme déjà créé.
On peut imaginer plusieurs techniques pour générer un tel arbre binaire. Mandelbrot utilise des arborescences fractales (cf [BD88]). Nous utilisons les techniques précédemment développées dans les chapitres 3 et 4 générant stochastiquement une arborescence binaire à partir d'une matrice de ramification ( respectivement une matrice d'évolution) traduisant la répartition des ordres de Strahler (respectivement les ordres d'évolution) dans l'arbre, ordres qui nous servirons pour l'établissement de la géométrie et l'imposition de contraintes géométriques.
Un tel arbre binaire est d'office planaire en ce sens qu'il peut être dessiné dans le plan en respectant les notions de droite et de gauche pour ses fils, deux arêtes ne se coupant pas en dehors de leurs extrémités : les algorithmes de dessin automatique d'arbres binaires dans le plan sont nombreux ([WS79], [RT81] ou [Ar88]).
La racine de l'arbre est le seul nœud qui ne possède pas de père. Il est intéressant d'ajouter une arête appelée arête racine à partir de la racine pour matérialiser l'embouchure d'un fleuve, cf figure 6B.
6.2.2 Algorithme de construction d'une carte topologique planaire quasi-triangulaire admettant un arbre binaire donné comme arbre recouvrant
La définition d'une carte topologique (cf chapitre 2 auquel nous renvoyons pour les principales définitions et notations) nécessite la définition pour chaque sommet du cycle des arêtes qui en sont issues. On retrouve là la définition combinatoire d'une carte donnée par Cori [Co75] et la classique implantation d'une carte par listes chaînées de successeurs. De façon à éviter un trop grand formalisme qui nuirait à l'intuition, nous avons préféré dans les algorithmes suivants qui concernent la construction de cartes topologiques planaires, présenter l'insertion d'une nouvelle arête dans un cycle à l'aide d'une figure (voir par exemple la figure 6A) présentant sur le plan le cycle considéré et la nouvelle arête insérée à sa place.
Nous présentons dans ce paragraphe une modélisation topologique complète d'un bassin fluvial. L'intérêt de disposer d'une telle modélisation sera de pouvoir ensuite y adjoindre différentes modélisations géométriques. La modélisation topologique d'un bassin fluvial étant une carte topologique planaire, l'adjonction d'un modèle géométrique est alors un problème de dessin automatique de cartes planaires avec contraintes (naturellement liées à la réalité de l'objet). Nous proposons dans ce chapitre, un algorithme automatique de dessin par segment de droite, des cartes planaires définies dans les paragraphes suivants.
Disposant d'une modélisation topologique d'un réseau fluvial par un arbre binaire, le bassin fluvial ou de drainage, c'est à dire la portion de surface drainée par ce réseau fluvial, peut être modélisé en première approximation (Figure 6B) par une carte planaire que nous allons choisir quasi-triangulaire et admettant cet arbre planaire comme arbre recouvrant (i.e. les sommets de l'arbre sont ceux de la carte et l'ensemble des arêtes de l'arbre est inclus dans l'ensemble des arêtes de la carte) :
Principe de l'algorithme
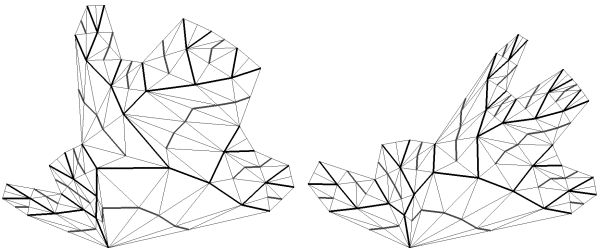
Le principe de construction de la carte topologique planaire quasi-triangulaire admettant un arbre binaire sous-jacent donné comme arbre recouvrant (Figure 6B, photographie 6A, planche 13A haut) consiste à faire croître le bord extérieur de cette carte par ajouts successifs de sommets et d'arêtes au cours du parcours en largeur de l'arbre binaire topologique initial. A chaque fois qu'un nœud interne de l'arborescence est traité (le nœud correspondant dans la carte est obligatoirement situé sur le bord extérieur de la carte courante), on ajoute à la carte courante les deux fils de ce nœud ainsi que cinq arêtes de manière à rendre la carte connexe et reconstituer un nouveau bord extérieur.
Ordre de traitement des nœuds
Les nœuds internes de l'arbre sont parcourus au cours d'une descente en largeur, c'est à dire niveau de profondeur après niveau de profondeur à partir du nœud racine et de droite à gauche pour les nœuds d'un même niveau (Figure 6B). Ainsi un nœud interne est toujours parcouru avant ses deux nœuds fils.
On vérifiera facilement que cet ordre de traitement associé au type de traitement décrit ci-après impliquent que le nœud courant n traité est automatiquement sur le bord extérieur de la carte planaire en cours de création.
Traitement d'un nœud interne
Soit un arbre possédant N nœuds internes. Chaque nœud n (numéroté de 1 à N) interne à l'arbre binaire et sur le bord extérieur de la carte planaire quasi-triangulaire en cours de construction est traité de la façon suivante :
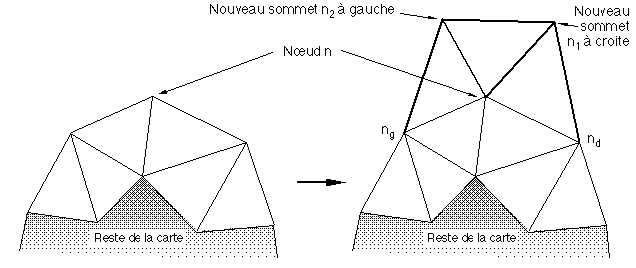
Figure 6A : Agrandissement de la carte planaire courante par insertion de nouveaux nœuds et arêtes : traitement du nœud interne n.
On ajoute à la carte, à l'intérieur de sa face extérieure (Figure 6A), deux nœuds, n1 à droite et n2 à gauche, qui matérialiseront dans la carte les nœuds fils droit et gauche de n dans l'arbre. On crée ensuite dans la face extérieure deux arêtes entre n1 et n, et n2 et n (arêtes qui correspondent à celles de l'arbre et qui à ce titre matérialiseront le parcours réel de la rivière) ainsi qu'une arête entre n1 et n2. Enfin, de manière à reconstituer un nouveau bord extérieur, on crée une arête entre n1 et le nœud nd situé à droite de n sur l'ancien bord extérieur de la carte, et une arête entre n2 et le nœud ng situé à gauche de n sur l'ancien bord de la carte (Figure 6A). A chaque itération de la génération de la carte 2 sommets et 5 arêtes sont donc ajoutés. Le nœud traité étant sur le bord extérieur de la carte, l'ajout des 2 sommets et des 5 arêtes dans la face extérieure de la carte de départ crée bien (évident) une nouvelle carte planaire.
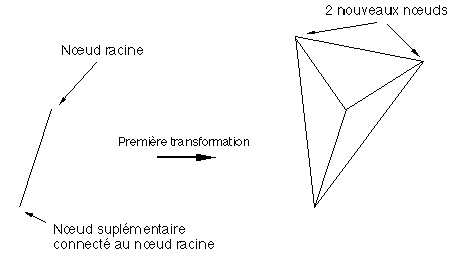
Figure 6C : carte initiale et son évolution.
Après le traitement successif de tous les nœuds internes contenus dans l'arbre, la carte est créée comme le montre la figure 6B (voir planche 13A bas).
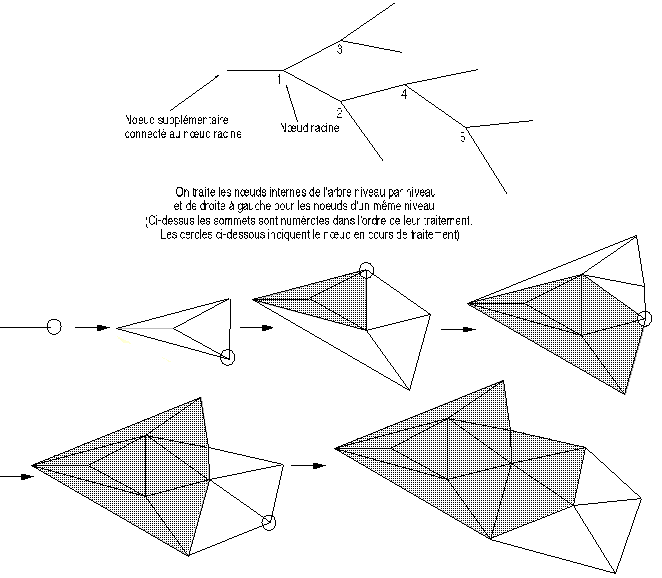
Figure 6B : Création d'une carte planaire quasi-triangulaire admettant un arbre binaire donné comme arbre recouvrant de la carte à partir de l'arbre initial.
Remarque
Au départ la carte initiale est composée de 2 nœuds, le nœud racine lié à un nœud supplémentaire par une arête (Figure 6C). L'opération de traitement d'un nœud interne est donc possible dès le nœud racine.
6.2.3 Caractérisation globale de la carte topologique quasi-triangulaire précédente
Nous donnons ici une autre caractérisation globale de la carte planaire construite admettant un arbre binaire recouvrant donné (Figure 6D). Cette caractérisation sera utilisée pour prouver la planarité géométrique de l'algorithme de dessin du paragraphe 6.3.1.
L'arbre binaire peut être décomposé en un ensemble de "zones interfluviales" délimitées par deux sous-branches issues d'un nœud interne de la façon suivante :
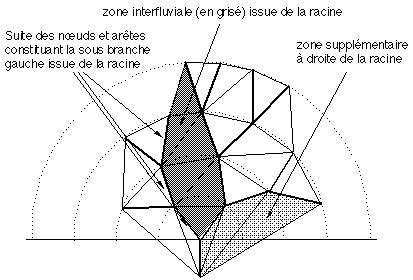
Figure 6D : Caractérisation globale de la création de la carte topologique (Les cercles représentent les niveaux dans l'arbre).
(1) A tout nœud interne on associe l'unique zone délimitée par la sous-branche gauche (resp. droite) issue de ce nœud et constituée de son fils gauche (resp. droit) suivis de tous ses descendants à droite (resp. gauche) jusqu'à une feuille de l'arbre.
(2) On adjoint à la racine deux zones supplémentaires à gauche et à droite : la zone à gauche (resp. à droite) est délimitée par la suite des nœuds descendants à gauche (resp. droite) issue de la racine et par la sous-branche constituée de l'arête supplémentaire joignant la racine au sommet supplémentaire ajouté.
Théorème
La carte quasi-triangulaire planaire construite par l'algorithme du paragraphe 6.2.2 est obtenue en triangularisant toutes les zones interfluviales de la façon suivante (Figure 6D) :
Considérons les deux sous-branches délimitant la zone interfluviale considérée. On insère des arêtes entre :
- les nœuds de même niveau sur les deux sous-branches,
- tout couple de nœuds de niveau n de la sous-branche gauche et de niveau n+1 de la sous-branche droite,
- le nœud terminal de la plus courte des deux sous-branches et les nœuds de niveau supérieur de l'autre sous-branche.
Preuve : Evident.
Remarque
Ces insertions d'arêtes s'effectuent au niveau topologique (c'est à dire qu'elles sont insérées dans un ordre précis dans les cycles d'arêtes issus des sommets de la carte en cours de construction). La figure 6D montre sur un exemple dans quel ordre les arêtes sont insérées dans les cycles des sommets.
Cette modélisation se révélera insuffisante au niveau géométrique et la carte planaire quasi-triangulaire modélisant le bassin fluvial nécessite deux types de raffinement :
(1) Introduction des lignes de crêtes sous formes d'arêtes de la carte, associée à une retriangularisation de la carte planaire quasi-triangulaire.
(2) Subdivision récursive locale de la carte courante (chaque triangle subdivisé étant remplacé par quatre triangles), cf [FF82], de façon à rendre compte de la complexité fractale de la surface montagneuse dans certaines régions (loin des vallées).
6.2.4 Création de lignes de crêtes
La modélisation topologique présentée ci-dessus n'est pas suffisante.
Dans la réalité géographique une rivière suit le chemin de gradient (de pente) maximum d'un relief. Les deux facettes adjacentes à chacune des arêtes matérialisant une rivière devront donc être inclinées de manière à recréer cette pente. La triangularisation topologique proposée aux paragraphes précédents ne permet pas de créer cette condition nécessaire. Dans la carte générée toutes les arêtes joignent des sommets faisant partie des fleuves, toutefois, certaines de ces arêtes ne matérialisent pas un fleuve car elles joignent deux nœuds de deux bras de rivières parallèles. Si une arête de ce type est dessinée par segment de droite, il est impossible de créer un point d'altitude maximum entre ses deux sommets extrémités et donc de constituer la pente générant les deux bras de rivière. Ceci est dû à l'absence dans notre modèle de la notion de ligne de crête, séparant dans la réalité deux bras de rivière issus de leur point de confluence.
La solution adoptée consiste à créer dans la carte ces lignes de crêtes de manière à générer réellement au niveau topologique des vallées dans lesquelles s'écouleront les rivières modélisées par l'arbre topologique. Une ligne de crête séparera chaque couple de bras de rivière issus d'un point de confluence n (un nœud interne) et sera placée à l'intérieur de la zone interfluviale associé à n. Elle sera modélisée par une ligne polygonale associée de manière unique au nœud n qui lui donne naissance et séparera les sous-arbres gauche et droit de ce nœud. Cette modélisation topologique permettra de faire apparaître lors du plaquage de la géométrie, l'alternance à tous les niveaux de la carte de points hauts (crêtes) et de points bas (rivières et vallées) qui existe dans la réalité.
Il est facilement vérifiable que pour générer ces lignes de crête topologiques, il suffit de créer sur chacune des arêtes de la carte n'appartenant pas à l'arbre binaire initial (réseau fluvial) un sommet supplémentaire dit sommet de crête (Figures 6E-6F, photographie 6A, planche 13B haut). Une fois tous ces sommets ajoutés il reste à triangulariser la carte qui contient alors des facettes à quatre ou à cinq cotés. On distingue deux traitements suivant le type de facette à retriangulariser :
- Soit il y a seulement un sommet supplémentaire sur la facette qui comportait donc deux arêtes rivières pour côtés. Les facettes de ce type forment les jonctions entre rivières.
- Soit il y a deux sommets supplémentaires sur la facette qui ne comportait alors qu'une seule arête rivière.
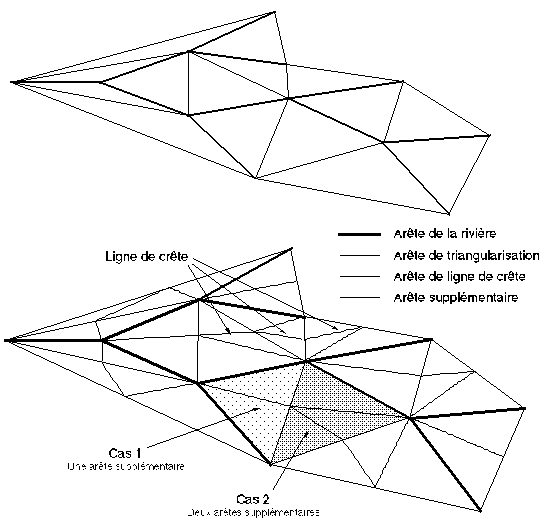
Figures 6E et 6F : Carte sans et avec lignes de crêtes.
Dans le premier cas la triangularisation est évidente, on crée à l'intérieur de la facette une nouvelle arête entre le nœud n formant la jonction entre les deux rivières et le sommet supplémentaire (qui sera le sommet de départ de la ligne de crête séparant les deux bras du réseau fluvial attenant au nœud n).
Dans le second cas, on crée à l'intérieur de la facette, une arête entre les deux sommets ajoutés (arête qui appartiendra à une ligne de crête) et une autre arête pour achever la triangularisation de la facette à quatre côtés restante (position choisie avec équi-probabilité parmi les 2 positions possibles) (Figures 6E-6F, Photographie 6A, planche 13B haut).
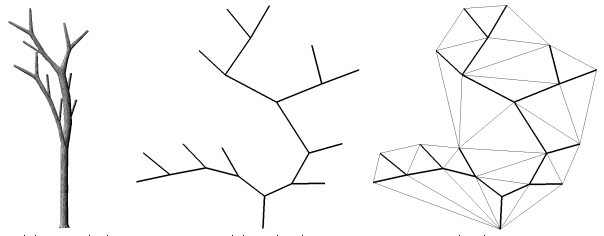
Arbre topologique Arbre planaire Carte planaire
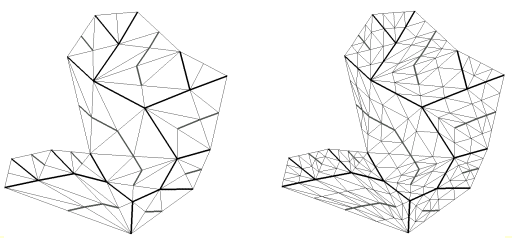
Carte
planaire avec lignes de crête
Carte planaire avec lignes de crête
après une fractalisation globale
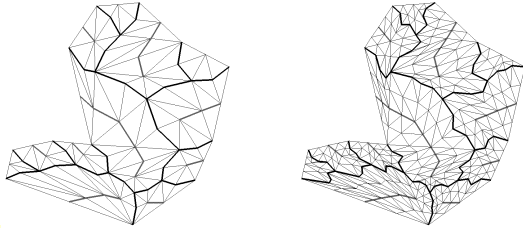
Carte planaire avec lignes de crête
Carte planaire avec lignes de crête
après une fractalisation sur les rivières (Coef. 0,5)
après une fractalisation globale
et une fractalisation sur les rivières (Coef. 0,5)
Photographies 6A : Algorithme de dessin d'arbre et de carte planaire
Remarques
(1) Les insertions de sommets et d'arêtes effectuées dans l'ordre cyclique tel que montré figure 6E définissent bien une nouvelle carte planaire (évident)
(2) Cette modélisation des lignes de crête a pour conséquence évidente que le sous-arbre de tout nœud interne est encadré et séparé du reste de l'arbre par deux lignes de crêtes (celles respectivement à gauche et à droite des branches gauche et droite de ce sous-arbre). Cette remarque importante est le point de départ de l'algorithme de plongement dans le plan de l'arbre binaire (Paragraphe 6.3.1), algorithme dans lequel à tout nœud interne est associé un secteur angulaire de développement de son sous-arbre (Paragraphe 6.3.1.2), secteur angulaire qui est une première approximation au niveau géométrique du bassin fluvial associé au sous-arbre issu du nœud interne et limité par les deux lignes de crêtes sus-mentionnées.
(3) En donnant aux nœuds des lignes de crête créées des altitudes calculées selon les lois du paragraphe 6.3.4, un relief impliquant l'écoulement du fleuve tel qu'il est voulu par le dessin de l'arbre en projection dans le plan xOy (position des rivières et sens d'écoulement) pourra être obtenu.
6.2.5 Opérations topologiques supplémentaires
Un certain nombre d'opérations topologiques supplémentaires peuvent être effectuées pour augmenter le nombre de facettes et donc disposer d'un modèle plus précis, pouvant être fractal dans certaines zones élevées de la montagne. La conservation de la planarité de la carte topologique par ces opérations est évidente.
Fractalisations
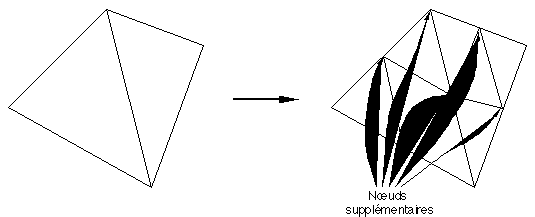
Figure 6G : Fractalisation globale
Il est possible d'effectuer une ou plusieurs fractalisations globale ou partielle pour augmenter le nombre de facettes de la carte. Toute facette dans une zone prédéfinie est alors décomposée en quatre nouvelles facettes par création d'un nouveau nœud sur chacun de ses cotés et liaison de ces nœuds au moyen de trois nouvelles arêtes (Figure 6G), voir [FF82]. A chaque fractalisation globale de la carte, le nombre de facettes est multiplié par quatre, avec création d'un nombre de sommets supplémentaires égal au nombre d'arêtes avant l'opération.
Cette triangularisation a été choisie plutôt que celle consistant à créer seulement un nouveau nœud à l'intérieur de la facette considérée et à le relier avec les trois sommets. En effet, le parcours géométrique d'une rivière entre deux confluents n'est que rarement rectiligne. En introduisant des nœuds sur les arêtes des facettes on pourra rendre plus chaotique l'écoulement de la rivière en projection dans le plan en créant par exemple des méandres (voir planches 13B bas et 13C bas).
Fractalisation sur les arêtes rivières
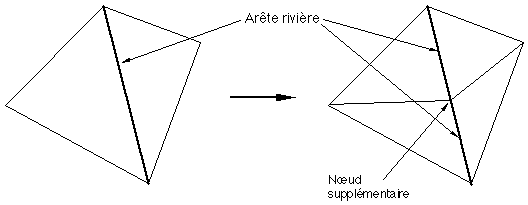
Figure 6H : Fractalisation sur les rivières
Le problème ci-dessus peut être résolu d'une manière différente si on ne désire pas multiplier le nombre de facettes par 4 à chaque fractalisation. Par l'opération de fractalisation sur les rivières, on ne crée des nœuds supplémentaires que sur les arêtes rivières. Pour conserver une carte quasi-triangulaire, lors de la création d'un nœud sur une arête rivière R, deux nouvelles arêtes devront lier ce nœud aux deux sommets opposés à R des deux facettes adjacentes (Figure 6H, planche 13C).
6.3 Modélisation géométrique d'un bassin fluvial
Dans ce paragraphe, nous proposons un algorithme linéaire de dessin automatique dans le plan par segments de droite de la carte planaire quasi-triangulaire précédente modélisant un bassin fluvial. Cet algorithme de plongement reprend les trois étapes de la génération topologique par :
- traitement des nœuds de l'arbre sous-jacent,
- traitement des nœuds des lignes de crête,
- traitement des sommets surajoutés.
Il restera dans un second temps à attribuer une altitude à tous les sommets de cette carte pour en avoir une représentation filaire 3D (Photographie 6C, planche 13D haut).
6.3.1 Algorithme de dessin d'un arbre binaire dans le plan respectant des contraintes de densité de nœuds
6.3.1.1 Positionnement général de la méthode
La méthode de placement des nœuds dans le plan consiste à mettre tous les sommets de l'arbre de même niveau de profondeur sur un même demi-cercle. Tous ces demi-cercles du demi-plan y>0 sont concentriques, centrés sur le nœud racine de position (0,0) (Figure 6I). Le nœud supplémentaire introduit dans l'arbre à l'initialisation de l'algorithme (connecté à la racine) adopte une position d'ordonnée négative qui sera précisée ultérieurement.
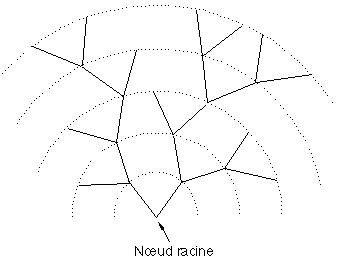
Figure 6I: Positionnement des nœuds sur des arcs concentriques
Une constatation importante est que même en s'enfonçant en profondeur dans l'arbre, les sommets de niveau identique n'auront pas trop tendance à se regrouper, le rayon des arcs allant croissant. La densité de nœuds sur les différents arcs de cercles peut toutefois varier de façon assez importante dans la mesure où le nombre de nœuds sur les différents niveaux peut être multiplié par deux à chaque niveau, alors qu'il n'est pas possible d'adopter une loi quadratique fonction du niveau pour le rayon des différents arcs (la longueur des segments de rivière ne doit pas trop varier).
6.3.1.2 Secteur angulaire de développement d'un sous-arbre
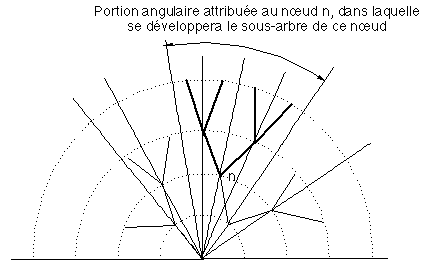
Figure 6J : Secteurs angulaires associés aux nœuds
Pour tout nœud n de l'arbre, on définit (Figure 6J)
- un secteur angulaire (d'origine la racine de l'arbre) dans lequel le sous-arbre issu de n sera dessiné,
- la position de n sur la portion d'arc découpée par ce secteur angulaire sur le demi-cercle correspondant à son niveau, position fixée selon une règle présentée ci-dessous.
L'algorithme de définition de ces secteurs angulaires est récursif respectant la règle de partage suivante qui assure la planarité de l'arbre binaire dessiné :
Définition : Règle de partage
Les secteurs associés aux deux fils droit et gauche d'un nœud n seront respectivement les deux sous-secteurs à droite et à gauche obtenus en partageant le secteur du nœud père n par la demi-droite issue de la racine et passant par n (dite demi-droite de partage associée à n).
Seul le cas de la racine pose problème puisque la demi-droite de partage de son secteur (secteur d'angle
p dans lequel se développe l'arbre entier) n'est pas définie : la définition de cette demi-droite et ses conséquences seront abordées ci-dessous. Dès lors, une fois connue la règle de positionnement d'un nœud sur son arc, l'algorithme d'attribution d'un secteur à chaque nœud n et de positionnement de n dans son secteur s'effectue récursivement niveau par niveau de droite à gauche pour les nœuds de même niveau, par l'opération de partage décrite ci-dessus. Cet algorithme "de partage récursif" assure la planarité de l'arbre binaire dessiné.6.3.1.3 Position des nœuds et intégration de contraintes de densité de sommets
Pour intégrer des contraintes du type "densité de nœuds dessinés dans une région", on utilise la taille du secteur angulaire attribué à tout nœud n de façon à l'adapter à l'importance du sous-arbre dépendant de n.
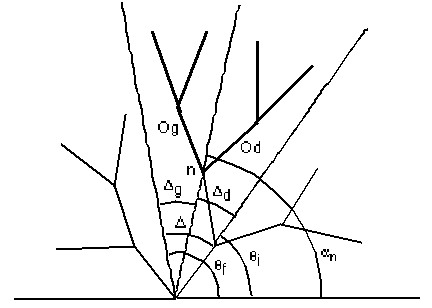
Figure 6K : Utilisation des ordres
Les tailles relatives des deux secteurs angulaires attribués aux deux nœuds fils d'un nœud père étant fonction de la demi-droite de partage et donc de la position du nœud père sur son arc, il suffit pour intégrer ce type de contrainte, de positionner le nœud père sur son arc par une formule barycentrique (voir paragraphe suivant) fonction de l'importance relative des deux sous-arbres de ses fils. L'importance du sous-arbre d'un nœud n sera mesurée par un ordre On (cf paragraphe 6.3.3 pour le choix de ces ordres qui apparaissent sur la figure 6K près des extrémités finales des arêtes) attribué à n.
Pour pouvoir appliquer l'algorithme du 6.3.1.2, il nous reste à définir la demi-droite de partage pour la racine et à donner la formule définissant la position d'un nœud dans son secteur angulaire.
6.3.1.4 Positionnement d'un nœud dans son secteur, de la demi-droite de partage associée à la racine et du sommet supplémentaire lié à la racine
Soit le nœud interne n, auquel est attribué par l'algorithme de partage récursif ci-dessus, le secteur angulaire situé entre les angles
qi et qf du référentiel global. Ce secteur est de taille angulaire qf - qi = D > 0. L'abscisse angulaire de n sur le demi-cercle de son niveau, à partir de l'axe horizontal de référence sera alors donnée par la formule barycentrique : an = qi+Cette formule a pour conséquence que les tailles angulaires
Dd =On choisit la demi-droite de partage associée à la racine de façon à séparer le demi-plan en deux secteurs de tailles proportionnelles aux deux sous-arbres de la racine. A cette fin, cette demi-droite de partage fera avec le demi-axe Ox horizontal de référence l'angle
Dd donné par la formule ci-dessus (avec D égal à p, Od et Og étant les ordres respectifs des fils droit et gauche de la racine).Il est alors naturel de situer le nœud supplémentaire sous la racine, sur le prolongement de cette demi-droite de partage.
Une condition supplémentaire, très naturelle dans le cadre du réalisme des images obtenues, doit être ajoutée au positionnement des nœuds dans leurs secteurs respectifs :
L'angle en tout nœud interne entre la demi-droite de partage issue de ce nœud et l'arête droite ou gauche issue de ce nœud dans l'arbre doit être inférieur à 90°.
Cette condition peut facilement être implantée : il suffit lorsqu'on positionne un nœud (par la formule ci-dessus) de déterminer l'angle obtenu au niveau de son père entre la demi-droite de partage qui en est issue et l'arête le joignant à son nœud fils. Si cet angle est supérieur à 90°, il faut alors rapprocher le nœud fils de la demi-droite de partage jusqu'à obtenir un angle inférieur à 90°. Cette éventualité est en fait très rare, elle n'a jamais eu à être appliquée dans toutes les simulations réalisées. Elle est cependant importante à imposer pour la correction de la preuve (ci-dessous) de la planarité de la carte quasi-triangulaire.
Connaissant l'angle de placement d'un nœud, on peut le positionner définitivement dans le plan si on connaît le rayon de l'arc de cercle sur lequel il sera placé. Ce rayon pourra être par exemple une fonction linéaire croissante du niveau de profondeur du sommet considéré.
Remarques
- Un nœud fils droit a toujours un angle de placement plus petit que celui de son père. Un nœud fils gauche a toujours un angle de placement supérieur à celui de son père. La démonstration est triviale car la position angulaire d'un nœud correspond à la limite entre les deux portions angulaires auxquelles il peut donner naissance, donc le sous-arbre droit évoluera obligatoirement à droite (en coordonnées angulaires), le sous-arbre gauche évoluera obligatoirement à gauche. Cette contrainte est l'analogue au niveau angulaire de la contrainte réalisée au niveau de l'abscisse par l'algorithme de Knuth (cf chapitre 2).
- La planarité de l'arbre est évidente car tous les sous-arbres issus de nœuds de même niveau évoluent dans des portions angulaires disjointes.
6.3.2 Algorithme de dessin par segments de droite de la carte planaire quasi-triangulaire modélisant le bassin fluvial
Le dessin dans le plan et par segments de droite de la carte finale avant relèvement de ses sommets se fait selon les deux étapes décrites du point de vue topologique au paragraphe 6.2 :
(1) La première étape, correspondant à l'opération topologique du paragraphe 6.2.1 (Photographie 6A) consiste à triangulariser l'arbre à présent dessiné dans le plan (par ajout d'arêtes segments de droite joignant des sommets de l'arbre) de façon à définir une carte planaire quasi-triangulaire admettant cet arbre comme arbre recouvrant. Il nous faut prouver que l'ajout des 5 arêtes (segments de droite) correspondant au traitement d'un nœud est possible sans intersection non désirée avec d'autres arêtes de la carte.
(2) La seconde étape (Paragraphes 6.2.4 et 6.2.5, Photographies 6A) consiste à ajouter des sommets à chaque facette triangulaire de la carte quasi-triangulaire précédente dessinée par segments de droite et à retriangulariser ces facettes par l'ajout de nœuds et d'arêtes (segments de droite) : cette étape est possible de façon évidente et retourne une nouvelle carte quasi-triangulaire planaire dessinée par segments de droite.
6.3.2.1 Dessin par segments de droite de la première étape
A cette étape tous les sommets de la carte sont positionnés puisque ce sont les sommets de l'arbre binaire plongé dans le plan au paragraphe 6.3.1. Pour prouver que la carte est planaire, il nous suffit donc de prouver que les arêtes ajoutées (sous forme de segments de droite joignant des couples de sommets) selon l'algorithme du paragraphe 6.2 n'ont aucune intersection entre elles ou avec les arêtes de l'arbre, en dehors de leurs extrémités. Cette propriété découle de la règle de partage des secteurs angulaires de développement donnée au paragraphe 6.3.1.2 et du théorème de caractérisation globale de la triangulation donnée au paragraphe 6.2.3. On a en effet les propositions :
Proposition :
(1) On considère un nœud interne n de l'arbre, la demi-droite de partage Dn et la zone interfluviale Zn qui en sont issues (Figure 6L).
a) La demi-droite de partage issue du nœud interne n sépare les deux sous-branches délimitant la zone interfluviale issue de n et coupe toutes les arêtes de triangulation joignant des nœuds appartenant à ces deux sous-branches, en un point unique ("point de crête").
b) On note ng(k) et nd(k) les deux nœuds de même niveau k sur les deux sous-branches gauche et droite de Zn. Alors pour h et l tels que h > l = k (resp. h < l = k) les segments ng(l)nd(l), ng(l)nd(h), ng(h)nd(l) sont situés dans le demi-plan supérieur (resp. inférieur) délimité par la droite ng(k)nd(k).
c) Quels que soient ng(k) et nd(l), le segment ng(k)nd(l) est inclus dans le polygone de la zone interfluviale Zn.
(2) Toutes les propriétés du (1) restent vraies pour les deux zones supplémentaires ajoutées à droite et à gauche de la racine (paragraphe 6.2).
(3) Des points (1) et (2), on déduit que la carte topologique quasi-triangulaire C obtenue par ajout de segments de droites à partir de l'arbre binaire dessiné selon l'algorithme du paragraphe 6.3.1 est bien un dessin planaire par segments de droite de la carte topologique définie au paragraphe 6.2.
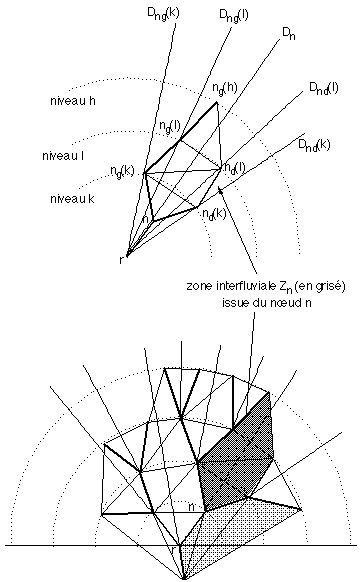
Figure 6L : Dessin planaire par segments de droites de la carte planaire quasi-triangulaire
Preuve
(1.a) Ce point est une conséquence directe de la définition de la demi-droite de partage issue de n. En effet, cette demi-droite partage le secteur de développement du sous-arbre dépendant de n en deux sous-secteurs gauche et droit de développement des sous-arbres gauche et droit de n.
(1.b) Soit r la racine et k=l<h.
Situations relatives de ng(l)nd(l) et ng(k)nd(k) :
Le cône C(k) de sommet r et constitué des deux demi-droites de partage Dn
g(k) = r ng(k) et Dnd(k) = r nd(k) est une réunion (règle de partage) de secteurs de développement contenant plus d'éléments que la réunion constituant le cône C(l) de sommet r limité par Dng(l)= r ng(l) et Dnd(l) = r nd(l). La corde ng(l)nd(l) découpée par C(l) sur le demi-cercle de niveau l (=k) est alors nécessairement (démonstration évidente) dans le demi plan supérieur délimité par la corde ng(k)nd(k) découpée par C(k) sur le demi-cercle de niveau k.Situations relatives de ng(h)nd(l) et ng(k)nd(k) :
En conséquence de la règle de partage, Dn
g(h) = rng(h) est une demi-droite strictement incluse dans le cône C(l). De plus le demi-cercle de niveau h est extérieur au demi-cercle de niveau l. Donc le point ng(h) est dans le demi-plan supérieur délimité par le segment ng(l)nd(l), est donc a fortiori dans le demi-plan supérieur délimité par le segment ng(k)nd(k). En conséquence le segment ng(h)nd(l) est situé dans le demi-plan supérieur délimité par ng(k)nd(k), puisque joignant deux points dans cette situation.Les autres situations relatives se prouvent par des arguments analogues.
(1.c) L'inclusion du triangle (n, ng(k), nd(l)) dans Zn est encore une conséquence de la règle de partage. En effet tout sommet s sur la sous-branche gauche entre n et ng(k) appartient à une demi-droite de partage rs extérieure au cône de sommet r et limité par Dn
g(k) = r ng(k) et Dnd(l) = r nd(l) et est donc extérieur au triangle (r, ng(k), nd(l)). Or l'angle au nœud n des deux arêtes filles de n étant inférieur à 180° (condition supplémentaire définie à la fin du paragraphe 6.3.1), le point n est intérieur au triangle (r, ng(k), nd(l)). Donc le sommet s est a fortiori extérieur au triangle (n, ng(k), nd(l)). Il en est de même pour les sommets de la sous-branche droite. En conséquence, le triangle (n, ng(k), nd(l)) est inclus dans Zn, d'où le résultat.(2) On vérifie facilement que les preuves des points (1.b) et (1.c) s'appliquent pour les deux zones supplémentaires issues de la racine et dont l'une des sous-branches est constituée de l'arête supplémentaire positionnée dans la suite de la demi-droite de partage issue de la racine. Le point (1.a) reste vrai pour chacune de ces deux zones supplémentaires si on leur donne pour lignes de partage respectives, les demi-axes horizontaux qu'elles contiennent.
(3) On déduit du théorème de caractérisation globale, du (1.b), du (1.c) et du (2) que les arêtes ajoutées dans une zone interfluviale sont deux à deux disjointes (en dehors de leurs extrémités) et sont incluses dans la zone, c'est à dire n'ont pas d'intersections non voulues avec d'autres arêtes ajoutées ou appartenant à l'arbre.
Par ailleurs, les situations relatives entre arêtes ajoutées dans une zone interfluviale, prouvées au (1.b) assurent que ces arêtes ont bien été insérées à la place prévue au paragraphe 6.2 dans les cycles des sommets : cette carte planaire dessinée par segments de droite est donc bien un plongement dans le plan de la carte topologique du paragraphe 6.2.
6.3.2.2 Dessin par segments de droite de la seconde étape
Pour modéliser des lignes de crêtes dans la carte quasi-triangulaire précédente, un sommet supplémentaire (Figure 6E, Photographie 6A) est créé sur chacune des arêtes n'appartenant pas à l'arbre binaire initial (réseau fluvial). Il existe différentes façons de choisir la position dans le plan de ce sommet. Par exemple, une conséquence des points (1.a) et (2) de la proposition précédente est que les demi-droites de partage définissent un tel point unique par intersection avec chaque arête ajoutée. Le choix de ce point conduit cependant à des lignes de crêtes rectilignes, ce qui nuit grandement au réalisme. Aussi avons nous préféré choisir la position de chacun des sommets ligne de crête à l'exact milieu de l'arête sur laquelle il est placé. La retriangularisation par ajout d'arêtes rectilignes supplémentaires dans les facettes ainsi créées à 4 ou 5 côtés ne pose aucun problème d'intersections non désirées car elles sont obligatoirement convexes (géométriquement triangulaires).
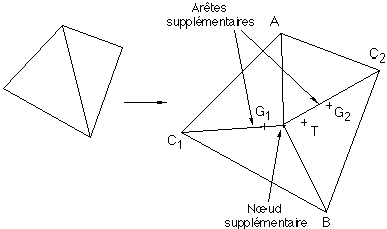
Figure 6M : Position d'un nouveau sommet
Le placement des sommets supplémentaires introduits au cours des différentes fractalisations permet de rendre la carte moins régulière. En ne plaçant pas les nœuds supplémentaires associés aux arêtes rivières exactement entre les deux anciennes extrémités de l'arête, on rend le cours de la rivière beaucoup moins linéaire. Pour cela, une méthode barycentrique a de nouveau été utilisée. Le nouveau sommet va être placé en une position intermédiaire entre les centres G1 et G2 des deux facettes adjacentes à l'arête considérée (Figure 6M). L'algorithme de placement est le suivant :
Choisir au hasard avec équi-probabilité l'une des facettes
adjacentes à l'arête
Affecter le poids 1 aux deux extrémités de l'arête
Affecter le poids C_PONDERAL au centre de la facette choisie
Affecter au nouveau sommet la position barycentrique
entre les 2 extrémités de l'arête et le centre
de la facette affectés de leurs coefficients respectifs
Plutôt que de choisir strictement au hasard la facette à l'intérieur de laquelle est déporté le nouveau sommet, il est possible de choisir systématiquement la plus grande, de manière à réduire les différences d'aire pouvant exister entre les facettes.
Une valeur du coefficient numérique C_PONDERAL égale à zéro placera le nouveau sommet entre les deux anciennes extrémités, plus C_PONDERAL sera grand plus la nouvelle position sera proche de l'un des centres des deux facettes adjacentes.
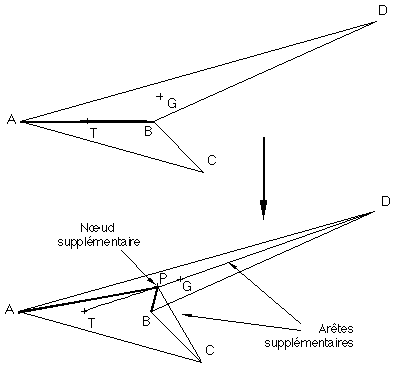
Figure 6N : Aberration de planarité lors du déplacement d'un nouveau nœud rivière
Il existe un cas particulier où cette méthode de placement n'est pas valable. Quand le quadrilatère formé des quatre sommets A, P, B et C n'est pas convexe (voir figure 6N où ABC et ABD sont les deux facettes ayant pour arête commune AB sur laquelle on désire créer un nœud supplémentaire P, T est le centre de l'arête AB et G le barycentre de la facette ABD dans laquelle on a choisi de placer le nouveau sommet P), le dessin de la carte topologique planaire n'est pas géométriquement planaire La valeur de C_PONDERAL sera alors fixée temporairement à 0.
6.3.3 Le choix de la fonction d'ordre
Un ordre doit être attribué à chacun des nœuds de l'arbre. Pour imposer des contraintes efficaces de densité de sommets, il est judicieux de choisir une fonction d'ordre permettant de quantifier l'importance du sous-arbre dont dépend le nœud concerné. Dans le cadre des lois données au paragraphe 6.3.1.4 l'ordre utilisé devra être positif, d'autant plus grand que le sous-arbre dépendant du nœud est important.
Un premier choix consiste à utiliser les ordres de Strahler [St52] qui, rappelons le, matérialisent assez bien l'importance des arêtes à l'intérieur de l'arbre. Plus le nombre de Strahler d'un nœud est important, plus le sous-arbre dépendant de ce nœud est topologiquement important, plus le sous-arbre est susceptible d'être large, et donc plus la portion angulaire de développement qui lui est attribuée est large de manière à ce qu'il puisse évoluer le plus librement possible. Les résultats obtenus sont corrects (Photographie 6B).
Ordres de Strahler r r r Largeur maximale du sous-arbre
Photographies 6B : Influence de la loi d'ordre sur la géométrie de la carte planaire
On peut bien entendu utiliser les ordres d'évolution, même s'ils perdent ici une grande part de leur intérêt (la croissance de la structure topologique). De la même manière que pour les modèles géométriques de dessin d'arbres (ordre d'évolution corrélé négativement avec l'importance des nœuds), on devra alors tenir compte de l'âge de l'arbre pour revenir à des valeurs voisines des nombres de Strahler par un changement de variable.
Une autre possibilité consiste à utiliser pour fonction d'ordre la largeur maximale de l'arbre dont le nœud considéré est la racine (Photographie 6B). L'ordre d'un nœud n sera donc le nombre maximum de nœuds rencontrés sur l'ensemble des niveaux du sous-arbre dont n est la racine.
Enfin, une dernière possibilité simple est de considérer que l'ordre d'un nœud est le nombre de nœuds du sous-arbre auquel il donne naissance. On a de nouveau ici un ordre dont le calcul est linéaire du nombre de nœuds de l'arborescence.
6.3.4 Remontée des points
Nous disposons actuellement d'un modèle topologique et de son dessin dans le plan par segments de droites. La définition entière de la géométrie de la carte requiert le calcul de la coordonnée en z de chacun de ses sommets (coordonnée en z qui représentera l'altitude du sommet) (Photographies 6C et 6D, planche 13D). Suivant le modèle topologique adopté (carte simple, carte avec lignes de crête, carte avec diverses triangularisations supplémentaires), la carte topologique est composée soit de sommets appartenant uniquement au réseau fluvial (premier cas), soit de ces mêmes nœuds auxquels viennent s'ajouter les sommets issus de la création des lignes de crête, et éventuellement les nœuds supplémentaires créés au cours de triangularisations.
Le calcul des coordonnées en z des sommets va s'effectuer dans le même ordre que la construction de la carte topologique, c'est à dire :
- un premier traitement pour les sommets de la rivière (arbre sous-jacent),
- puis le cas échéant, un second traitement pour les nœuds des lignes de crête (traitement simultané à leur création et utilisant l'altitude des points des rivières),
- enfin autant de traitements que de triangularisations successives en utilisant pour les sommets de triangularisation les coordonnées en z des nœuds déjà définis.
Cette décomposition en étapes à l'avantage de permettre de représenter le relief à différents niveaux de modélisation et donc de précision (Paragraphe 6.4.2).
6.3.4.1 Altitude des sommets de l'arbre sous-jacent
La seule condition à vérifier pour le calcul des coordonnées en z des sommets des rivières est que l'altitude d'un sommet quelconque de l'arbre soit supérieure à celle de son père (Figure 6O). Dans le cas contraire, au mieux on verra la création de lacs sur les rivières, au pire le réseau fluvial ne sera plus valide. Cette loi étant vérifiée, une grande liberté nous est laissée pour fixer l'altitude des sommets les uns par rapport aux autres.
On peut choisir par exemple :
- une loi totalement aléatoire,
- une loi dépendant des ordres des nœuds,
- une loi dépendant de la longueur des arêtes.
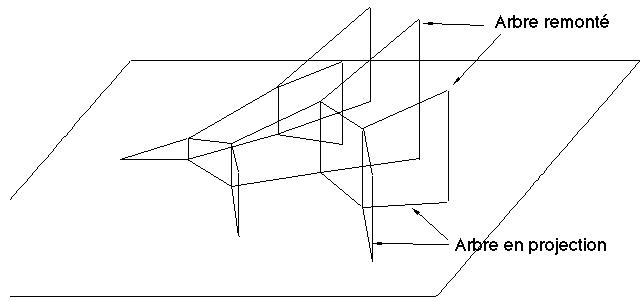
Figure 6O : Altitudes des sommets de l'arbre sous-jacent.
Toutefois, le relief d'un réseau fluvial est généralement plus tourmenté dans son cours supérieur que dans son cours inférieur. Ceci est dû à l'apparition progressive de bassins sédimentaires qui aplanissent le relief au cours du temps. Une loi de calcul de l'altitude permettant de rendre compte de ce phénomène sera telle que la différence d'altitude d'un nœud par rapport à son père soit d'autant plus élevée que ce nœud sera plus profond dans l'arbre.
L'utilisation de la fonction d'ordre de Strahler [St52] (croissant des feuilles, pour lesquelles il vaut un, à la racine de l'arbre, pour laquelle il est maximum) permet de programmer une loi rendant compte empiriquement de cette propriété géomorphologique. Une formule de calcul définissant la prise d'altitude d'un nœud par rapport à son père pourra être :
DALT(NRIV) = ![]()
où CRIV est un coefficient numérique, NRIV un nœud de la rivière et a un exposant réel positif.
Les ordres d'évolution (croissant de la racine vers les feuilles de l'arbre binaire) pourraient aussi être utilisés. La formule de calcul définissant la prise d'altitude d'un nœud par rapport à son père sera alors positive croissante de l'ordre d'évolution, par exemple :
DALT(NRIV) = Evolution(NRIV)a * CRIV
où CRIV est un coefficient numérique et a un exposant réel positif.
6.3.4.2 Altitude des sommets des lignes de crête
L'altitude de chacun des sommets des lignes de crête va être évaluée en fonction de l'altitude des sommets du réseau fluvial attenant. Une fois que les altitudes de tous les sommets de la carte auront été fixées, le sens d'écoulement de l'eau sur les facettes devra être tel que le réseau fluvial soit correctement constitué en position et en direction et que les lignes de crête soient bien des lignes de crête. Les facettes adjacentes à un nœud P situé sur une ligne de crête (n'importe quelle facette de la carte) peuvent être de deux types (paragraphe 6.2.3) (Figure 6P) :
- soit elles ne contiennent qu'un seul nœud de ligne de crête et donc l'arête opposée à ce nœud est une rivière (facette de type (1)),
- soit elles contiennent deux nœuds formant une ligne de crête et le sommet opposé à cette arête est situé sur une rivière (facette de type (2)).
Chaque facette du premier type devra posséder des coordonnées telles que la direction de sa ligne de pente maximale assure la formation d'une des rives de l'arête rivière en étant dirigée vers cette arête rivière. Chaque facette du second type devra être inclinée de telle manière que l'orientation de sa ligne de pente maximale assure la présence de la ligne de crête en s'éloignant de cette ligne de crête.
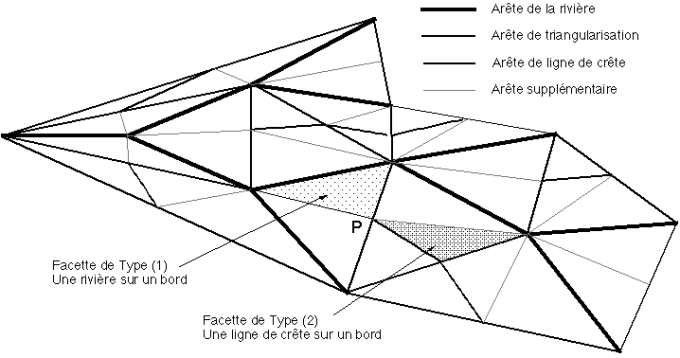
Figure 6P : Deux types de facettes pour le calcul de l'altitude du sommet de crête P.
6.3.4.2.1 Critères de validité de la pente des facettes
Dans la suite les nœuds constituant chaque ligne de crête issue d'un nœud interne n de l'arbre sont numérotés Pi(xi,yi,zi), i=1, dans l'ordre où on les rencontre à partir de n.
Etant donnée une ligne de crête, la condition de pente de chaque facette qui lui est incidente impose une contrainte sur l'ordonnée inconnue de chaque nœud de la ligne de crête appartenant à la facette. On obtient ainsi deux types de contraintes sur les ordonnées inconnues zi des Pi, en fonction des deux types de facettes.
Contrainte associée à une facette de type 1 (bordant une rivière)
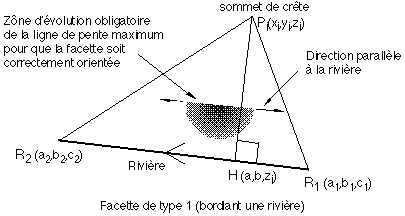
Figure 6Q : Altitude du sommet de crête pour une facette de type 1
Le cas limite de validité d'une telle facette est réalisé lorsque la ligne de pente maximale est parallèle à la rivière (Figure 6Q). Or cette ligne de pente est orthogonale à la direction de l'horizontale dans la facette. L'altitude zi minimale que peut donc adopter le sommet Pi est donc telle que la droite horizontale PiH passant par Pi soit perpendiculaire à la rivière, c'est à dire telle que les vecteurs PiH et R1R2 soient orthogonaux. Cette valeur minimale correspond à une direction de pente maximale parallèle à l'arête rivière et pour toute valeur de zi supérieure, la pente est dirigée vers l'arête rivière. Ainsi avec les notations de la figure 6Q, zi doit vérifier l'inégalité
Contrainte associée à une facette de type 2 (bordant une ligne de crête)
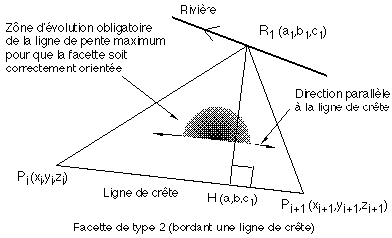
Figure 6R : Altitude du sommet de crête pour une facette de type 2
Dans une telle facette contenant deux sommets de crête Pi et Pi+1, les ordonnées zi et zi+1 de Pi et Pi+1 sont inconnues.
Le cas limite de validité d'une telle facette est également réalisé lorsque la ligne de pente maximale est parallèle à la ligne de crête (Figure 6R). Or cette ligne de pente est orthogonale à la direction de l'horizontale dans la facette. La situation limite est donc atteinte lorsque la droite horizontale R1H passant par R1 est perpendiculaire à la ligne de crête, c'est à dire lorsque les vecteurs R1H et PiPi+1 sont orthogonaux. La bonne inclinaison de la facette remplace cette égalité par l'inégalité linéaire (démonstration non donnée ici) impliquant zi et zi+1 (avec les notations de la figure 6R) :
![]()
On remarquera que les coefficients de
zi+1 et zi dans cette inéquation ne sont autres que les produits scalaires ![]() .
.![]() et
et
6.3.4.2.2 Calcul des altitudes
Déterminer les altitudes inconnues des nœuds constituant une ligne de crête revient donc à résoudre le système d'inéquations linéaires associées aux différentes facettes qui lui sont incidentes :
Pour f, facette du type 1 et Pi le nœud de crête sur f : zi
³ c(f)Pour f, facette du type 2 et Pi et Pi+1 ses nœuds de crête : a(f)zi + b(f)zi+1
³ c(f)où a(f), b(f), c(f) sont des constantes dépendant de f.
On montre facilement que ce système d'inéquations admet au moins une solution en remarquant que si l'on impose que tous les points Pi aient la même ordonnée inconnue z (pour tout i, zi
³ z), alors les inéquations précédentes associées aux faces f s'écrivent toutes z = c(f) (car a(f)+b(f)>0, voir formule ci-dessus du paragraphe 6.3.4.2.1), où c(f) est une constante dépendant de f. Ces inéquations étant en nombre fini, la solution est alors évidente.On peut alors à l'aide des techniques classiques de programmation linéaire (méthode du simplexe, par exemple, voir [Sa84]) chercher parmi toutes ces solutions celle qui rend minimum une fonction linéaire donnée des zi.
6.3.4.3 Création d'un bord à la carte
Lors de la phase de dessin, pour obtenir un rendu plus réaliste, il est nécessaire de munir la carte d'un bord vertical. Cette opération à pour but de renforcer l'impression de relief pour une vue éloignée.
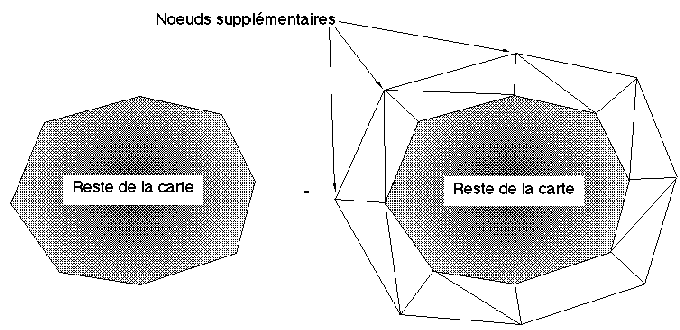
Figure 6S : Création d'un bord de facettes sur une carte
Ce bord sera composé d'un ensemble de facettes surajoutées. Ces facettes supplémentaires peuvent être gérées de deux manières, soit par création temporaire lors du dessin, soit, plus simplement, par modification de la carte topologique de manière à les inclure au cours de la modélisation. En effet, il peut être ajouté une épaisseur de facettes sur tout le pourtour de la carte topologique. La figure 6S montre la manière avec laquelle ces facettes sont créées par création d'un nouveau nœud pour chaque nœud de l'ancien bord, et liaison de ce nœud à la carte par trois nouvelles arêtes. Au moment du calcul de la géométrie de la carte, les coordonnées allouées aux nouveaux sommets assureront que ces facettes soient bien verticales (On ne les dessine pas lors du plongement planaire de la carte). Toutes les opérations de manipulation géométrique ayant à être effectuées pour le dessin pourront alors être réalisées globalement.
6.3.4.4 Altitude des sommets issus d'une triangularisation supplémentaire
Chacun des sommets supplémentaires est issu de deux sommets qui auparavant étaient liés par une arête. Une méthode simple de calcul de l'altitude de ce sommet consiste à adopter une valeur intermédiaire entre les altitudes des deux sommets initiaux (voir par exemple [Sm84]), ce qui amorce une fractalisation de l'arête traitée. Quatre nouvelles facettes d'orientations différentes sont générées à la place de chaque ancienne facette ce qui implique une amélioration de la qualité du dessin.
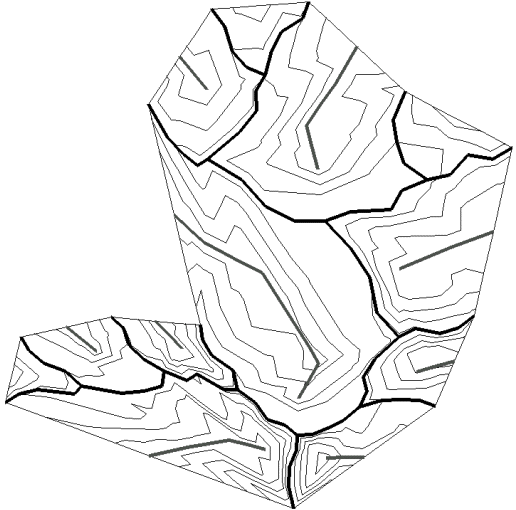
Photographie 6D : Lignes de niveau dans une carte
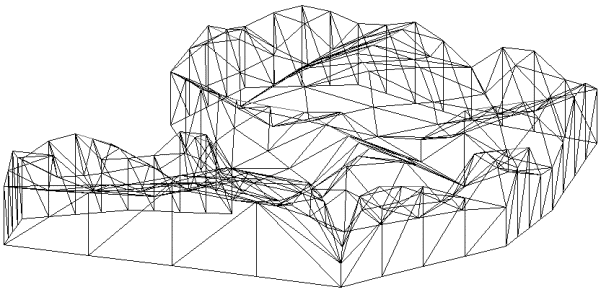
Photographie 6C : Vue filaire d'une carte remontée
6.4 Quelques résultats
Le rendu final des images sera détaillé au chapitre 8. Nous présentons ici l'influence des niveaux de modélisation topologique et géométrique sur l'image finale.
6.4.1 Influence de la forme de l'arbre topologique initial
La génération de l'arbre binaire topologique initial est prépondérante dans la forme globale du bassin fluvial généré. Les techniques de génération d'arbres binaires que nous avons décris aux chapitres 3 et 4 permettent à partir de matrices de ramification ou d'évolution particulières de générer des arbres binaires topologiques dont la "forme" est paramétrée par la matrice choisie. On constate par exemple sur les photographies 6E et 6F (modélisées avec des lois géométriques identiques de manière à rendre la comparaison possible) les différences morphologiques pouvant apparaître entre les bassins fluviaux générés à partir d'arbres topologiques binaires aléatoires et à partir d'arbres binaires aléatoires croissants.
Le premier bassin fluvial (Photographies 6E, planche 17A) issu d'un arbre binaire aléatoire est tout en longueur, avec un relief doux dans la partie inférieure du fleuve qui présente des méandres très prononcés et couvre une grande surface du relief. Ceci est dû à la forme particulière des arbres binaires aléatoires constitués essentiellement de très longs axes principaux de nombres de Strahler élevés (d'où une dénivellation faible par la loi fixant l'altitude des sommets du fleuve), sur lequel viennent se greffer de nombreuses petites rivières et sources de nombre de Strahler petit, provoquant une brusque montée du relief.
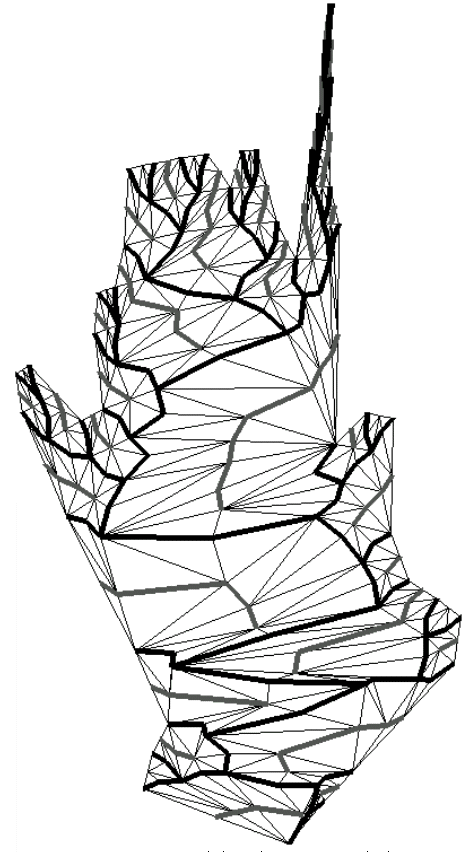
Carte 2D associée à un réseau fluvial modélisé par un arbre binaire aléatoire

Montagne et bassin fluvial associés à la carte de la photographie ci-dessus
Photographies 6E : Influence de la topologie de l'arbre binaire aléatoire sous-jacent.
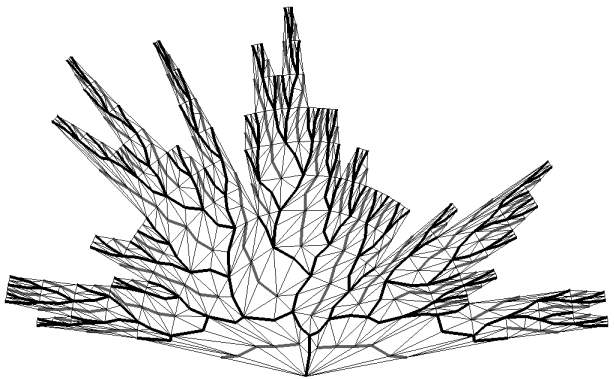
Carte 2D associée à un réseau fluvial modélisé par un arbre binaire aléatoire croissant

Vue du zénith du bassin fluvial associés à la carte de la photographie ci-dessus

Vue plongeante de la montagne et du bassin fluvial associés à la carte aux photographies ci-dessus
Photographies 6F : Influence de la topologie de l'arbre binaire aléatoire croissant sous-jacent.
Le second bassin (Photographies 6F) issu d'un arbre binaire aléatoire croissant est au contraire approximativement circulaire, présentant l'aspect d'un cirque dont le relief monte de façon beaucoup plus régulière que dans l'exemple précédent. Ceci est dû à la caractéristique propre aux arbres binaires aléatoires croissants qui sont bien équilibrés, c'est à dire qu'ils présentent à chaque niveau de profondeur de nombreuses branches de nombres de Strahler décroissant régulièrement vers les sources. On voit donc ainsi la génération d'un nombre important de confluents près de la racine de l'arbre. Il y a donc apparition de nombreuses vallées très profondes et très longues (ces vallées ressemblent presque à des gorges). Le cas extrême est atteint pour un arbre initial parfait (Photographies 6J et 6K, planche 17B).
6.4.2 Influence du niveau de modélisation topologique de la carte
A partir d'un même arbre binaire, les résultats graphiques seront d'autant plus réalistes que le niveau de modélisation topologique sera poussé (Photographies 6G). Il est en particulier impossible de ne pas générer de lignes de crête dans la modélisation du terrain (règle signalée au paragraphe 6.2.4). Par ailleurs les opérations supplémentaires de fractalisation permettent d'augmenter le réalisme d'un relief, tout particulièrement en évitant un aspect trop linéaire du fleuve. Signalons toutefois que ces retriangularisations éventuelles ne changent pas la forme globale du relief (forme de la rivière, importance du relief), les paramètres les plus importants restent la forme de l'arbre topologique initial pour la forme de la rivière en projection dans le plan et les paramétrisations géométriques pour le calcul des altitudes.
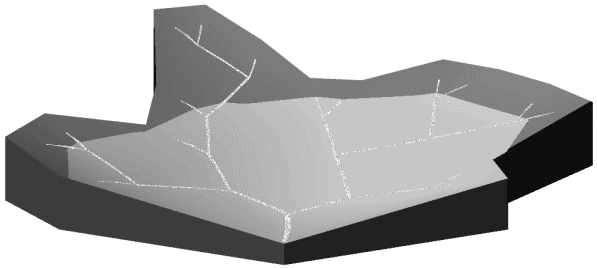
Triangularisation simple

Carte après création des lignes de crête

Carte après une fractalisation globale

Carte après une fractalisation globale et une fractalisation sur les rivières
Photographies 6G : Influence du niveau de modélisation topologique sur le réalisme du relief.
Ces sorties graphiques prouvent de manière évidente qu'il n'est pas possible d'utiliser la modélisation topologique sans lignes de crête. Cette étape ne peut être qu'intermédiaire au cours de la modélisation topologique d'un relief. On voit bien que les fractalisations améliorent le niveau de détail mais n'ont pas d'influence sur la constitution du bassin fluvial et l'importance du relief.
6.4.3 Influence des coefficients géométriques des lois d'altitude
Le paramètrage des coefficients numériques des lois géométriques permet de faire varier la prise d'altitude des sommets de la carte de manière à obtenir un relief possédant des caractéristiques spécifiques.
La photographie 6H montre par exemple un relief avec adoption d'une loi d'altitude constante des crêtes (paragraphe 6.3.4.2.2).
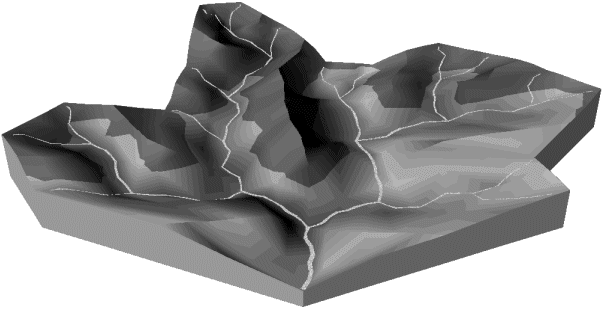
Photographie 6H : Application de la loi fixant une altitude constante à chaque ligne de crête
Il est aussi possible d'obtenir une variation globale de l'altitude affectant tous les sommets par résolution du système d'inéquations linéaires (cf ci-dessus) (Photographies 6I).

Loi par résolution du système d'équations, grande amplitude du relief

Loi par résolution du système d'équations, amplitude moyenne du relief
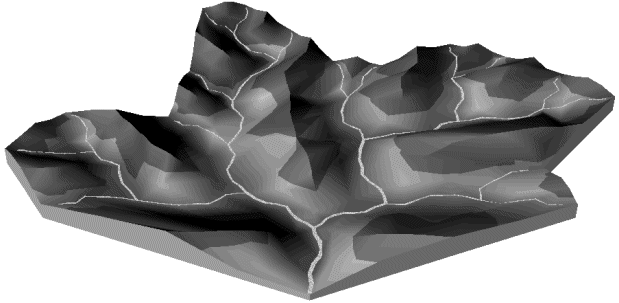
Loi par résolution du système d'équations, petite amplitude du relief
Photographies 6I : Paramètrage géométrique global sur l'amplitude du relief.
En jouant sur les coefficients géométriques des lois mathématiques pour le calcul de l'altitude des lignes de crête, on pourra obtenir des vallées plus ou moins profondes en induisant une plus ou moins grande différence d'altitude entre les rivières et les lignes de crête (Photographies 6J).

grande profondeur

profondeur moyenne

faible profondeur
Photographies 6J : Paramètrage géométrique de la profondeur des vallées. L'arbre binaire sous-jacent est un arbre binaire parfait.
Enfin, en jouant sur les lois de calcul de la prise d'altitude des rivières, on induira une croissance d'altitude du fleuve plus ou moins rapide (Photographies 6K).

Loi constante

Loi quadratique de l'ordre de Strahler
Photographies 6K : Paramètrage géométrique de la croissance d'altitude des fleuves.
6.5 Conclusion
Dans ce chapitre, un nouvel algorithme de plongement automatique dans le plan de cartes planaires quasi-triangulaires admettant un arbre binaire comme arbre recouvrant à été décrit. L’intérêt principal de cette méthode est qu’elle intègre la prise en compte de contraintes physiques du type "nombre de sommets en fonction de l'aire", problème connu comme difficile.
L'utilisation du concept d'arbre binaire modélisant le réseau fluvial sous-jacent à un relief est un outil puissant pour la synthèse d'images de montagnes. L'utilisation des ordres de Strahler ou des ordres d'évolution pour quantifier l'importance des différentes composantes d'un fleuve est naturelle dans la mesure où la structure de base est l'arbre binaire.
Les photographies présentées prouvent le haut degré de réalisme et la variété de formes qu'il est possible d'atteindre. Il faut signaler que les opérations requises par ce modèle, tant au niveau topologique que géométrique, ne nécessitent pas une puissance de calcul trop importante.
Après avoir prouvé la validité conceptuelle et la faisabilité matérielle de ce modèle, il reste à mieux intégrer la notion de matrice de ramification, mais surtout de matrice d'évolution dans le modèle. En effet, la topologie d'un fleuve peut être précisée à l'infinie. On pourra par exemple ne donner que le fleuve, ou bien que le fleuve et les rivières les plus importantes lui étant affluantes, ou bien le fleuve, ces mêmes rivières affluantes et les rivières affluantes de ces rivières,... On retrouve en fait ici les différentes générations de la croissance d'un arbre par matrice d'évolution. L'un des prochains aspects de la modélisation de relief sera de permettre ce raffinement progressif. Il est probable qu'il faudra définir de nouvelles opérations topologiques et géométriques.