Chapitre 7
Algorithmes et techniques
de rendu concernant les arbres
7 Algorithmes et techniques de rendu concernant les arbres
7.1 Introduction
Les problèmes concernant le rendu des nombreux modèles de végétaux ont été extensivement étudiés. Une présentation des principales techniques a été faite au chapitre 2. Nous présentons ici les solutions que nous avons développées. Leur caractéristique principale est de devoir s'exécuter sur un micro-ordinateur (un IBM PS/2 8580 avec possibilité de carte 8514A), ce qui impose des solutions algorithmiques efficaces pour obtenir des temps de calcul et d'affichage raisonnables.
Dans ce chapitre, on suppose présente en mémoire une arborescence topologique binaire quelconque plongée dans
R2 ou R3. De plus chacune des arêtes de cette arborescence est munie d’une épaisseur.Le problème est de dessiner cette arborescence avec les deux objectifs suivants:
- les caractéristiques topologiques de l’arbre binaire doivent être clairement visibles,
- le dessin doit être réaliste (y compris en gros plan).
La contrainte principale s’appliquant sur le dessin est que des arbres de plusieurs milliers d’arêtes, voir même plusieurs dizaines de milliers d’arêtes doivent pouvoir être représentés.
Ce chapitre présente deux techniques de dessin, l’une en 2D (dessin dans le plan), l’autre en 3D (3D projetée), permettant de remplir les deux objectifs fixés. La technique 2D est très simple et permet l'obtention rapide d’images suffisamment réalistes pour des arbres vus de loin. La technique 3D est considérablement plus évoluée de manière à pouvoir fonctionner correctement sur un ordinateur de faible puissance. Elle permet d’arriver à des dessins très réalistes (voir planches). Dans les deux cas, il sera possible d’adjoindre une texture à l’écorce, ainsi que des feuilles (description d’un modèle de conception et dessin de feuilles végétales).
7.2 Dessin 2D des arbres
Pour réaliser un dessin rapide, mais aussi pour obtenir une meilleure compréhension de l’influence des matrices de ramification ou d'évolution sur la forme de l'arbre généré, un algorithme de dessin en 2D (non volumique) est suffisant.
Une fois que les coordonnées dans
R2 de chaque nœud ont été calculées, chaque arête de l’arbre binaire géométrique n'est représentée que par un simple segment de droite (Photographie 7A). Chacune de ces arêtes apparaîtra à l’écran comme un rectangle de largeur calculée selon la loi d'épaisseur du modèle géométrique. Les jonctions entre les rectangles, correspondant aux nœuds de l'arbre, sont organisées comme on le voit sur la figure 7A. Le coin inférieur droit (respectivement gauche) du rectangle arête fils droit (respectivement gauche) vient se placer sur le coin supérieur droit (respectivement gauche) du rectangle arête père. Les deux triangles matérialisant explicitement le nœud à la jonction sont remplis.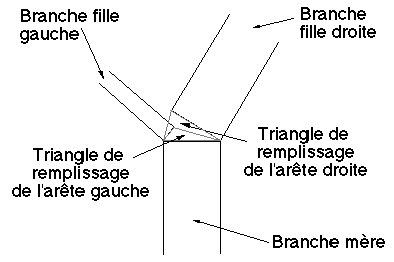
Figure 7A : Jonction par des triangles

Photographie 7A : un arbre en fil de fer Photographie 7A Bis: un arbre en 2D
Cette modélisation est manifestement très simple, il est à signaler qu'elle entraîne des erreurs minimes dans le placement des sommets mais l'aspect général de l'arbre n'en est que très légèrement changé, il n'y a en aucun cas modification de l'allure de l'arbre (Photographies 7A et 7A Bis).
Pour le dessin de la photographie 7B, les rectangles matérialisant les arêtes de l'arbre n’ont pas été remplis. On remarque que très peu de ces arêtes apparaissent réellement sous forme de rectangles. En effet, une conséquence du choix des lois géométriques est que si les arêtes de petits ordres ont une taille voisine ou inférieure au pixel, elles ne sont représentées que par un seul pixel. L’arbre dessiné peut avoir sensiblement plus de nœuds internes que ceux réellement visibles à l’écran (plus de 5000 nœuds internes pour l’arbre binaire de cette photographie).
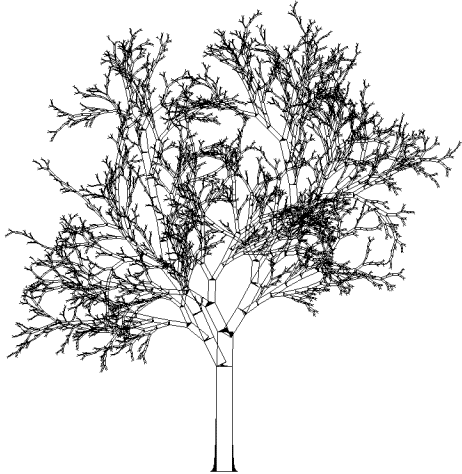
Photographie 7B : Un arbre en 2D sans remplissage
7.2.1 Un rendu réaliste même en 2D

Photographie 7C : Arbre avec texture 2D et sans texture 2D.
La visualisation en deux dimensions permet tout de même d'atteindre un certain degré de réalisme (Planches 1, 12A, B et C). Le modèle géométrique 2D comme le modèle 3D n'empêche aucunement les branches de se recouper les unes les autres ce qui remplace assez bien une vraie modélisation 3D (voir planches 1 et 2). Il faut toutefois pouvoir distinguer une branche d'une autre la recouvrant. Le plaquage d'une texture sur les branches est donc nécessaire. Celle-ci est obtenue en traçant des segments aléatoirement tiretés dans l’axe de chaque branche avec une couleur différente de celle du rectangle branche sous-jacent (voir photographie 7C et planches 1). Ce texturage ne fait pas apparaître chaque branche en volume (il n'y a pas d'ombrage), mais il est suffisant pour bien faire la distinction entre deux branches se recouvrant si elles sont orientées différemment.
7.3 Dessin 3D des arbres
7.3.1 Introduction

Photographie 7D : Dessin d'un arbre avec un éclairage
Comme lors du dessin en 2D, l'ensemble des coordonnées des nœuds de l'arbre est disponible mais cette fois dans
R3. On sait calculer les épaisseurs des branches au moyen de leurs ordres (par les formules données aux paragraphes 3.4.2 et 4.5.1). Le problème du dessin en trois dimensions est de modéliser l'arbre par un volume.Nous présentons dans la suite, un certain nombre de points importants concernant les buts à atteindre et la méthodologie de dessin. En particulier :
- Contrairement au modèle de dessin en deux dimensions, le modèle de dessin 3D devra autoriser un dessin identique pour un même arbre vu de points de vue différents. En particulier les positions des nœuds affichés devront correspondre parfaitement à celles données par le modèle géométrique.
- En première approximation les arêtes seront modélisées par des cônes (Paragraphe 7.3.2) et un modèle gérant les intersections de ces cônes au niveau des embranchements (Paragraphe 7.3.3) sera développé.
- La gestion des parties cachées au travers du dessin de chaque cône (Paragraphe 7.3.5) et au travers du placement des cônes les uns par rapport aux autres (Paragraphe 7.3.4) au cours du dessin va impliquer certaines approximations dans les recouvrements.
- Les aspects concernant à proprement parler le rendu des images seront enfin détaillés aux paragraphes 7.3.6, 7.3.7, 7.3.8 et 7.4. On y présente les modèles d'illumination et d'ombrage réalisés, les textures figurant l'écorce et un modèle de feuilles.
Dans tous ces aspects de la modélisation, il est important de minimiser le nombre d'objets à dessiner et le nombre de calculs à réaliser, tant en raison de la faible puissance d'un micro-ordinateur, que de la quantité limitée de mémoire disponible sur une telle machine. Ceci a présidé aux choix présentés ci-dessous et aux nouveaux algorithmes développés (modélisation d'un branchement par exemple) qui devront donc permettre ces minimisations.
7.3.2 Matérialisation des branches par des cônes : un premier modèle
Intuitivement les branches d'un arbre sont matérialisées dans l'espace par des cylindres. Dans la pratique ces cylindres apparaissent plutôt comme des cônes tronqués, en effet une arête matérialisant une branche aura deux extrémités d'épaisseurs non nulles et bien souvent différentes l'une de l'autre (Figure 7B).
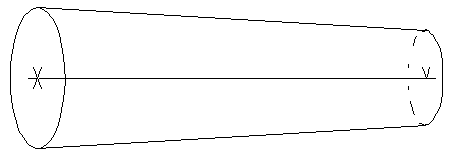
Figure 7B : Représentation d'une branche par un cône tronqué
Il est bien entendu que ces "cônes" ne pourront pas apparaître en tant que tels à l'écran, car il n'est pas possible de représenter directement des surfaces courbes. Chaque cône sera décomposé en un ensemble de facettes quadrangulaires planes ne se recoupant que sur leurs bords (Figure 7C) (Photographie 7E et planche 5A).
Le calcul de ces facettes s'effectue de la manière suivante :
On connaît l'axe du cône C à dessiner (donné par l'arête géométrique), sa longueur L ainsi que les épaisseurs à chacune de ses extrémités. On modélise ce cône à l'aide de facettes quadrangulaires définies de la façon suivante :
- On définit m demi-plans, bordés par l'axe du cône et
répartis également autour de cet axe (c'est à dire séparés par des angles de ![]() degrés).
degrés).
- On considère par ailleurs n+1 plans orthogonaux à l'axe du cône, équidistants, les deux extrêmes correspondant aux deux sections extrémités du cône (ils sont séparés par la distance L/n, où L est la longueur de l'axe du cône).
L'ensemble de ces m demi-plans et n plans transversaux coupent le cône selon des droites et des arcs de cercles constituant naturellement des facettes quadrangulaires courbes. Ces facettes définissent au total m*(n+1) points permettant de décomposer le cône tronqué en m*n facettes quadrangulaires planes (en substituant aux arcs de cercle des segments de droite, Figure 7C).
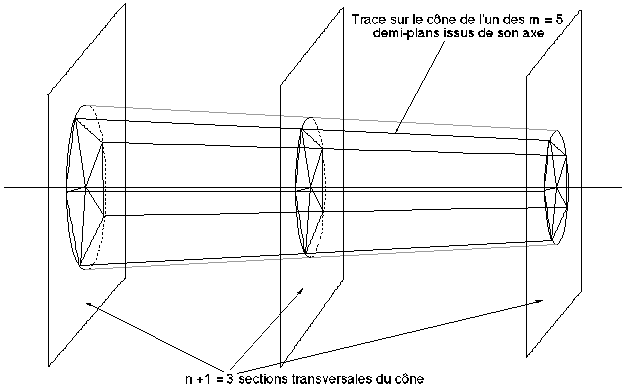
Le cône est partagé en n=2 sous-cônes successifs.
Figure 7C : Représentation d'une branche par facettes planes quadrangulaires.
Il est à remarquer que le fait de découper un cône en plusieurs sous-cônes (à l'aide des n+1 plans orthogonaux susmentionnés) peut ne pas paraître pertinent étant donné que les n facettes situées dans le même secteur d'espace situé entre 2 demi-plans successifs parmi les m issus de l'axe du cône, seront coplanaires et donc n'apporteront aucune qualité de dessin supplémentaire.
Aussi proposons nous dans le paragraphe suivant un modèle meilleur (introduisant une courbure des cônes) tant pour la représentation des branches que pour celle importante au niveau du rendu des embranchements.
7.3.3 Gestion des intersections entre les branches : un nouveau modèle.
7.3.3.1 Décomposition d'un arbre en branchements
Le problème consiste à joindre les trois cônes associés aux trois arêtes créant chaque nœud interne de l'arbre. La figure 7D montre que le raccordement de trois cylindres pose d'importants problèmes de recollement. Pour des raisons évidentes de réalisme du résultat, le collage doit être le plus parfait possible, et cela d'autant plus que nous avons la volonté de réaliser des vues en gros-plan sur les branches.
Contrairement à la méthode de dessin 2D, nous n'allons pas compléter les espaces laissés libres (comme réalisé par Kawaguchi [Ka82]) entre les bases des cônes modélisant les branches. Ceci est un problème simple en deux dimensions mais beaucoup plus compliqué en 3D car on devrait alors gérer de façon esthétique le remplissage de volumes. Chaque ensemble composé d'un nœud et des trois branches qui lui sont attenantes sera dessiné globalement. A cette fin, nous allons modifier la modélisation du dessin de l'arbre pour considérer qu'un nœud n'est plus créé par l'association de 3 cônes droits recollés (Figure 7D), mais seulement de 2 cônes qui seront courbés de manière à inclure la position géométrique du nœud (Figure 7E). Pour cette raison, dans la suite de ce chapitre, plutôt que de parler de dessin d'un nœud nous parlerons de dessin d'un branchement (branchement entre trois arêtes).
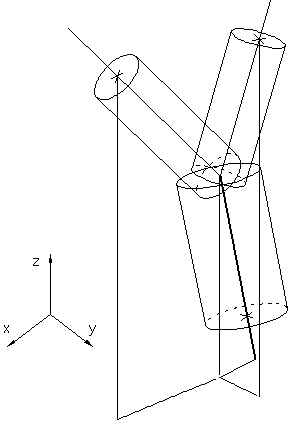
Figure 7D : Réalisation schématique d'un nœud
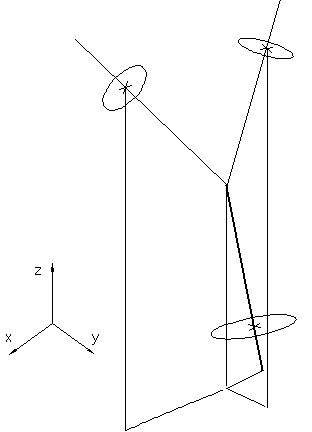
Figure 7E : Modélisation pour le dessin
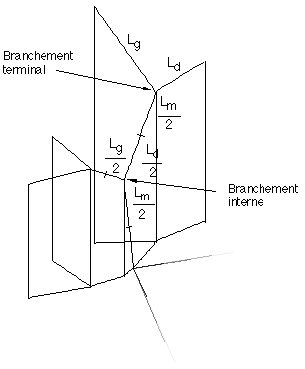
Figure 7F : Dessin orienté sur les branchements
Le dessin de l'arbre ne va plus consister à représenter à l'écran un assemblage de cylindres plus ou moins bien recollés au niveau des nœuds, mais à dessiner un assemblage de branchements. Chacun de ces branchements, associé à un nœud interne, inclura la moitié de l'arête mère de ce nœud et la moitié de chacune de ses arêtes filles s'il s'agit d'un branchement interne (les arêtes filles ne sont pas terminales). Dans le cas contraire, on a affaire soit à un branchement terminal (les arêtes filles sont terminales), auquel cas les longueurs prises en compte pour les arêtes filles sont les longueurs entières et non pas leurs moitiés, soit au branchement racine associé au nœud racine de l'arborescence, et alors la longueur donnée à l'arête mère racine est sa vraie longueur (Figure 7F).
Le raccordement entre les branchements s'effectue directement au milieu des arêtes sans aucune difficulté s'il y a correspondance entre les épaisseurs des sections en ce lieu.
7.3.3.2 Décomposition d'un branchement en deux cônes et sa facettisation
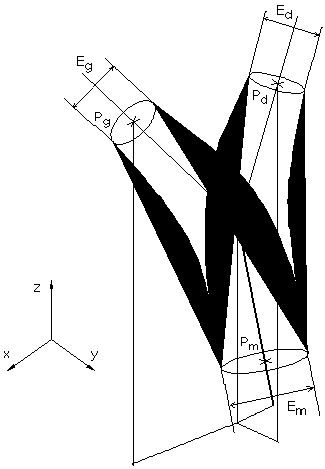
Figure 7G : Epaisseurs aux sections
Les informations nécessaires au dessin d'un branchement sont les positions 3D des quatre nœuds définissant le branchement (Pm, Pc, Pd et Pg) et les trois épaisseurs des trois demi-arêtes dessinées (Em, Ed et Eg) (voir figure 7G). La méthode de dessin consiste à modéliser séparément les deux couples d'arêtes (arête mère, arête fille droite) et (arête mère, arête fille gauche) comme deux cônes courbés. Les ensembles de facettes représentant ces deux couples d'arêtes sont seulement ensuite regroupés en un ensemble unique pour permettre ainsi le dessin du branchement.
La modélisation d'un cône rectiligne est, nous l'avons vu, relativement simple. Il faut maintenant le courber. Soit donc à dessiner le cône s'appuyant sur les points Pm, Pc et Pg. Les épaisseurs Em, Eg et Ec en Pm, Pg et Pc seront considérées comme connues (voir plus loin) pour les calculs suivants :
La première opération consiste à calculer les sections de notre cône au niveau des trois sommets. La section correspondant au point Pm est dans le plan orthogonal à l'axe PmPc passant par Pm. Celle au point Pg est dans le plan orthogonal à l'axe PcPg passant par Pg. Enfin, la section en Pc est incluse dans le plan bissecteur des deux précédents passant par Pc. Les sections dans ces trois plans seront circulaires (Figure 7H).
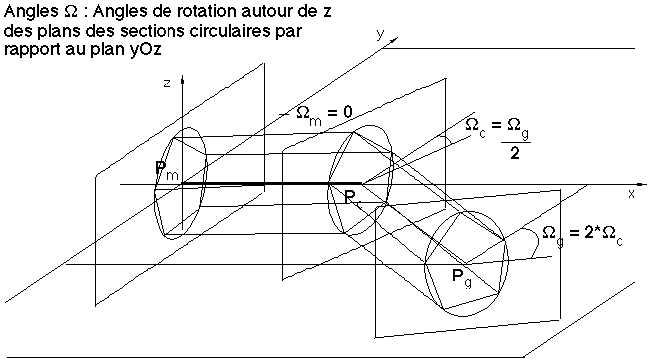
Figure 7H : Calcul des sections circulaires
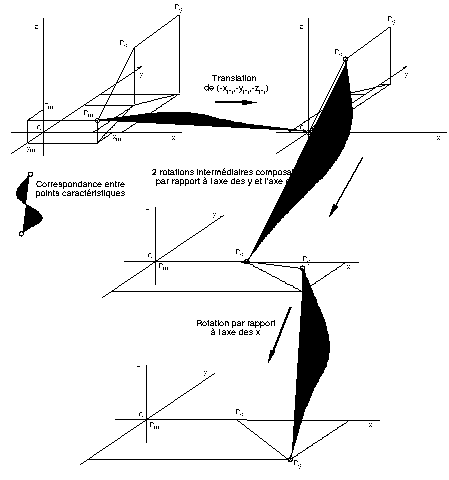
Figure 7I : Simplification par translation et rotations
Une simplification des calculs est obtenue en effectuant une translation suivie de trois rotations dans l'espace par rapport à y, z et x de telle manière que Pm devienne l'origine, PmPc l'axe des x et PcPg soit inclus dans le plan xOy (Figure 7I). Une fois cette transformation effectuée, il devient facile de calculer l'équation des trois plans contenant les sections. La section au point Pm est obligatoirement comprise dans le plan yOz. Les orientations des plans des deux autres sections sont obtenues par rotation du plan yOz autour de z d'un angle
Wg pour Pg et d'un angle Wm =Les 3 sections circulaires de centres respectifs Pm , Pc et Pg étant connues, On les discrétise en polygones réguliers constitués de m points (comme expliqué pour un cône seul, à l'aide de deux séries de m demi-plans régulièrement disposées respectivement autour des deux axes PmPc et PcPg et de façon à ce que ces deux séries fournissent la même discrétisation de la section centrale, selon la figure 7H).
Ainsi, cet ensemble de deux cônes (modélisant une arête mère et l'une de ses filles) est maintenant représenté par m séries de trois points naturellement en regard (Figure 7H).
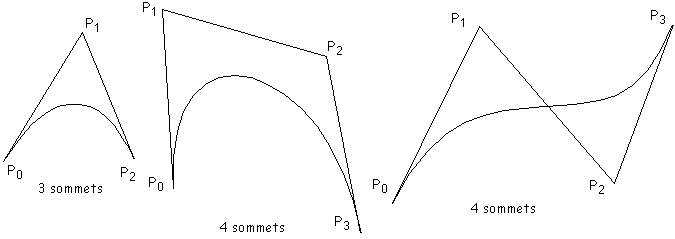
Figure 7J : Exemples de courbes de Bézier associées à des lignes brisées
Pour courber le cône de façon régulière nous allons utiliser des courbes de Bézier (Figure 7J). Celles ci permettent de réaliser le lissage d'une ligne brisée orientée. Si P0, P1, P2, P3, ..., Pn sont n+1 points formant une telle ligne brisée. La courbe de Bézier associée à cette suite de points est définie par l'équation suivante :
 avec t compris
entre 0 et 1.
avec t compris
entre 0 et 1.
L'utilisation des courbes de Bézier pour réaliser le lissage d'une ligne brisée répond à trois raisons principales:

Figure 7K : Répartition des points sur une courbe de Bézier
- La courbe de Bézier associée à un nuage de points ordonnés est tangente à la ligne brisée joignant ces points au niveau du premier et du dernier sommet (Figure 7K). Cette propriété est importante pour s'assurer que le recollement de deux branchements (au milieu d'une arête fille du premier et de l'arête mère du second) sera bien régulier.
- Les courbes de Bézier étant invariantes par transformations affines, les transformations géométriques (translations, rotations) qui vont être effectuées sur l'arbre ne modifieront pas son apparence. Il est important que le volume modélisé reste identique quel que soit le référentiel si on désire par exemple réaliser une animation.
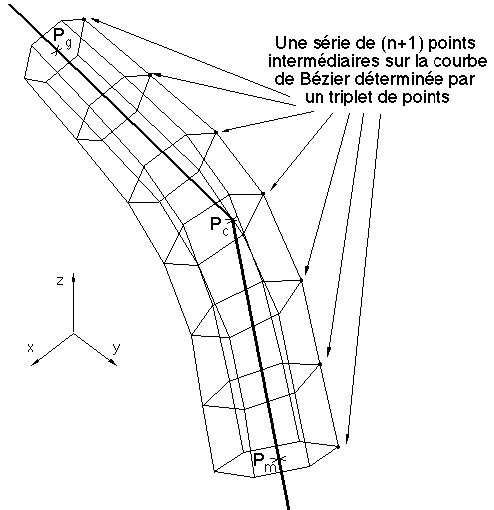
Figure 7L : Branche courbe dessinée par facettes
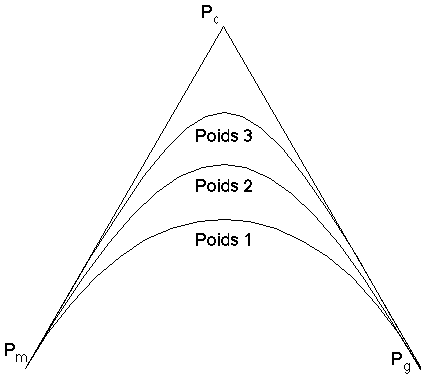
Figure 7M : Importance du poids du point central
- L'utilisation de ces courbes nous permet d'obtenir une approximation facile d'une suite de deux segments en une courbe lissée. Le calcul des points de la courbe s'effectue en faisant varier t de 0 à 1. Pour obtenir une courbe à n+1 points il suffira de faire varier t de 0 à 1 par incrément de 1/n. Les points obtenus ne seront pas régulièrement espacés, mais ils seront plus resserrés à l'endroit où l'on a besoin d'une plus grande précision, c'est à dire près du nœud central Pc au voisinage de la courbure maximum du cône (Figure 7K).
Chacun des triplets de points servira à calculer n+1 nouveaux points qui approximeront la courbe. A partir de ces (n+1)*m nouveaux points un ensemble de n*m facettes quadrangulaires matérialisant le cône tronqué est défini (Figure 7L).
Ce type de manipulation est possible pour chacun des deux cônes courbés (Pm,Pc,Pg) et (Pm,Pc,Pd). L'ensemble des facettes représentant un branchement pourra être constitué par regroupement des ensembles de facettes modélisant chacun de ses deux cônes courbés.
Utiliser une courbe de Bézier définie par seulement 3 points a pour inconvénient de ne pas accorder une assez grande importance au point intermédiaire : la courbe n'est pas assez incurvée, trop lissée. Dans ce cas, il peut même arriver que le branchement modélisé n'inclut pas le point P
c. Pour déporter la courbure dans la direction de Pc, il est possible de considérer que ce point est dédoublé, voir même triplé ou quadruplé. On lui affecte alors le poids 2, 3 ou 4 au lieu de 1 (Figure 7M).Remarque
Cette discrétisation au moyen de courbes de Bézier produit un écrasement de la section du cône courbé au voisinage du point Pc, toutefois cet écrasement peut être négligé dans la mesure où il ne devient réellement important que si les deux arêtes modélisées ont une très forte déviation l'une par rapport à l'autre (supérieure à 90°), ce qui ne se produit quasiment jamais avec nos modèles géométriques (écrasement non discernable sur la photographie 7E et la planche 5).
7.3.3.3 Une première réduction du nombre de facettes à gérer au niveau d'un branchement
Une méthode simple pour réduire le nombre de facettes à gérer consiste à supprimer toutes les facettes d'un cône qui pourraient se trouver à l'intérieur de l'autre cône. En effet, nous n'avons pas encore abordé le problème du choix des diamètres Em, Eg, Ed et Ec des sections. Un bon choix pour ces épaisseurs ne réduit en rien la qualité de la modélisation volumique et permet de réduire le nombre de facettes nécessaires au dessin. Les valeurs Em, Eg et Ed aux extrémités sont connues au moyen des fonctions d'épaisseur (voir paragraphes 3.4.2 et 4.5.1).
Deux possibilités et les choix associés pour Ec se présentent :
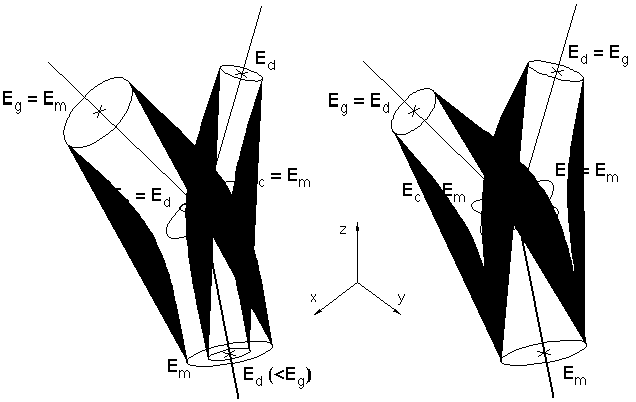
- soit on est en présence d'une fourche auquel cas Ed = Eg = épaisseur d'une des arêtes filles et Em = Ec = épaisseur de l'arête mère,
- soit une des branches filles est plus épaisse que l'autre ce qui implique que les épaisseurs du cône correspondant à la branche la plus importante sont toutes égales à Em et celle du cône de la branche la moins importante sont toutes égales à Min(Ed,Eg) (Figure 7N). Dans ce cas on ne dessine que deux cylindres courbes et non pas des cônes.
Embranchement non fourche fourche
Figure 7N : Diamètre des sections en fonction du type de biordre
Dans le premier cas (fourche) les cônes courbés ont une partie en commun. Dans le second cas le cône courbé de plus faible diamètre est en partie inclus à l'intérieur de l'autre. Les facettes "en double" dans le premier cas et incluse dans le gros cône dans le second cas peuvent être éliminées.
La connaissance des épaisseurs et des longueurs des segments de branches permet de paramétrer le nombre de facettes nécessaires à la modélisation de chacun des branchements. Il est possible d'obtenir des facettes d'une taille relativement constante quelle que soit la taille du cône modélisé. Le nombre (n-1) de points de Bézier intermédiaires est calculé proportionnellement à la longueur des cônes, le nombre m de sommets par section est proportionnel à l'épaisseur maximale du cône. Un minimum de 4 points de Bézier intermédiaires et de 6 sommets par section soit au total 30 facettes par cône est nécessaire pour une représentation précise et réaliste en gros-plan.

Photographie 7E : Représentation d'un embranchement (non fourche) par ses facettes et avec plaquage de texture.
On remarquera dans la photographie de gauche, le bon raccordement des facettes de la petite branche aux points d'entrée dans la grosse branche. Ceci est dû au fait que les points de Bézier sont moins espacés dans cette partie très courbée de la petite branche.
7.3.4 Affichage des facettes constituant un arbre
Le problème de la modélisation de l'ensemble des branches d'un arbre par un nuage de facettes est que le nombre total de facettes calculées devient très vite très grand. Par exemple, pour un petit arbre de 500 branchements (nœuds internes) qui seront chacun représentés au moyen d'un couple de cônes, chacun de ces cônes étant modélisé par un prisme courbe d'en moyenne 100 = 10*10 (m = 10 et n = 10) facettes, on calcule un nombre de 100000 facettes à afficher. Quel que soit l'algorithme de dessin utilisé (algorithme du peintre, Z-Buffer, ...), le temps de calcul risque d'être trop important pour rester réaliste (tout particulièrement sur micro-ordinateur). Au prix de certaines approximations, il est possible de simplifier le dessin, sans trop nuire au réalisme final tout en obtenant des temps de calcul et d'affichage beaucoup plus intéressants.
- Une première simplification a été décrite à la fin du paragraphe précédent: l'inclusion d'une partie du petit cône dans le grand cône associé à sa branche sœur (dans le cas d'embranchements non fourche) permet d'éliminer une partie des facettes à afficher. Dans le cas d'une fourche, les facettes constituant la partie des deux cônes associés à l'arête mère sont en double. Il suffit de n'afficher également que l'un des deux cônes au niveau de l'arête mère.
- Une autre simplification qui implique une approximation du dessin global consiste à représenter chacun des branchements indépendamment des autres. Si on reprend l'exemple précédent, ce n'est plus un ensemble unique de 100000 facettes qu'il faudra trier, mais 500 nuages de 200 facettes pour les 500 embranchements. Une fois réalisés ces 500 tris de 200 facettes, les 500 nuages indépendants seront bien entendu triés en z les uns par rapport aux autres pour conserver le réalisme du dessin.
Ce tri des embranchements est ainsi effectué de manière dynamique au cours de la phase de dessin par l'appel de la procédure récursive suivante sur le branchement racine :
Procedure DESSIN_ARBRE(BRANCHEMENT : branchement)
DESSINER_BRANCHEMENT(BRANCHEMENT) ;
si BRANCHEMENT n'est pas un branchement terminal alors
si Z_ECRAN(FILS_G(BRANCHEMENT))<Z_ECRAN(FILS_D(BRANCHEMENT) alors
DESSIN_ARBRE(FILS_G(BRANCHEMENT)) ;
DESSIN_ARBRE(FILS_D(BRANCHEMENT)) ;
sinon
DESSIN_ARBRE(FILS_D(BRANCHEMENT)) ;
DESSIN_ARBRE(FILS_G(BRANCHEMENT)) ;
fin_si
fin_si
fin_proc
Z_ECRAN est une fonction qui rend la coordonnée z à l'écran du nœud interne associé au branchement passé en paramètre (plus cette coordonnée est petite plus le point est situé à l'intérieur de l'écran), FILS_G (respectivement FILS_G) est une fonction qui rend le branchement fils gauche (respectivement droit) du branchement passé en paramètre, et DESSINER_BRANCHEMENT est la procédure réalisant le dessin d'un branchement.
Au moyen de cet algorithme le bon ordre de traçage des différentes branches est assuré de manière locale. La présence d'inversions de recouvrement entre branches ne peut pas être évité car le tri n'est pas complet. Ces inversions peuvent se produire car les branches filles d'un branchement interne quelconque sont dessinées dans leur intégralité l'une après l'autre. La première branche fille dessinée (celle dont le nœud racine a la profondeur écran la plus petite) sera donc intégralement dessinée derrière la seconde, alors que dans la réalité ces branches peuvent s'interpénétrer et se recouvrir mutuellement (cas de deux branches formant une double hélice par exemple).
Toutefois, ces inversions sont très difficiles à détecter sur un dessin unique car les branches sont, dans une très grande majorité des cas, dessinées de manière continue aux jonctions entre les branchements. Il n'existe qu'un seul cas particulier où certaines branches peuvent ne plus être continues à l'écran : on voit ainsi sur la figure 7O que si le dessin du premier sous-arbre fils A1 d'un branchement B vient recouvrir la zone de jonction entre B et son autre sous-arbre A2 (qui sera dessiné après que le sous-arbre complet A1 l'aura été) la branche fille initiant le sous-arbre A2 ne sera plus continue. Ce cas est relativement rare et impossible à détecter visuellement (voir photographies).
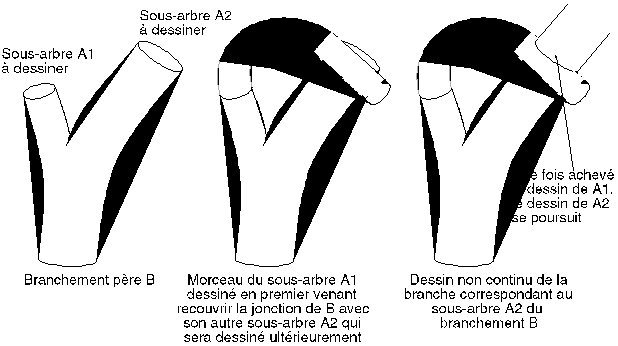
Fig 7O : Discontinuité dans le recollement des branchements
Dans la mesure où l'on ne désire réaliser que des images fixes, il est possible d'ignorer ces deux erreurs éventuelles, la continuité des branches obtenue quasi dans tous les cas étant un gage de qualité du rendu. Le problème posé par l'animation dans le cadre de cette méthode de dessin est que d'une image sur une autre il peut se produire des inversions d'ordre sur des branches, ce qui risque d'être visible.
7.3.5 Remarques sur la réalisation du tri des facettes sur un branchement et simplifications
7.3.5.1 Raisons du choix de l'algorithme du peintre dans la méthode de dessin des branchements
Une classification courante des algorithmes d'élimination des parties cachées en informatique graphique distingue deux types de méthodes :
- celles travaillant dans l'espace image (Z-Buffer,...),
- celles travaillant dans l'espace objet (Algorithme du peintre,...).
Dans la première classe, aucun traitement préalable sur les objets n'est effectué, car ils sont affichés les uns à la suite des autres par analyse séquentielle et comparaison par rapport à ce qui a déjà été affiché. On obtient donc des algorithmes linéaires du nombre d'objets (facettes) à dessiner (cf chapitre 8, paragraphe 2.1). Ces algorithmes sont les plus intéressants quand le nombre de facettes à afficher est important ou bien quand des traitements particuliers doivent être effectués sur les objets (plaquage d'une texture, lissage sur les couleurs ou bien encore si les facettes peuvent se couper ailleurs que sur leurs bords). Toutefois, il est important de souligner que la quantité de calcul à effectuer (en général décomposition point par point de chacun des objets), contribue à rendre ces méthodes assez peu efficaces dans le cas de petits ensembles d'objets.
La seconde classe regroupe des méthodes où les objets à représenter sont triés avec une relation du type "sera à dessiner avant". Ce type d'algorithme impliquant un tri, les temps de calcul pour l'affichage d'une image ne pourront pas être linéaire en le nombre de facettes à représenter. Si nous avions choisi de réaliser ce tri sur l'ensemble des facettes de l'arbre (N = 100 000 dans l'exemple précédent), les temps de calcul en N Log(N) auraient été prohibitifs sur un micro-ordinateur. Dans notre cas où il n'y a à représenter que des ensembles d'au plus quelques centaines de facettes (500 ensembles de 200 facettes), un simple tri en z des facettes sera plus rapide qu'une méthode de Z-Buffer, d'où notre choix de cette seconde méthode.
7.3.5.2 Traitement et dessin des facettes pour un branchement donné
Un premier problème est que le modèle de dessin des branchements avec union de deux sous-ensembles de facettes (un pour chacun des deux cônes courbés) pour chaque branchement n'empêche pas d'avoir des facettes se recoupant ailleurs que sur leurs bords. En effet, si B1 et B2 sont les ensembles de facettes associés aux sous-cônes courbés droits et gauche d'un branchement.
-
¢ (f1,f2) Œ B16B1, f1 et f2 ne se coupent pas ailleurs que sur leurs bords.-
¢ (f1,f2) Œ B26B2, f1 et f2 ne se coupent pas ailleurs que sur leurs bords.- Mais il peut exister certains couples de facettes (f1,f2) de B1
6B2 tels que f1 et f2 se coupent ailleurs qu'en leurs bords (au niveau de l'intersection des deux cônes courbés).La réalisation d'un tri des facettes pour le dessin s'en trouve compliquée car la gestion de la possibilité d'avoir des facettes se coupant entraîne l'écriture d'algorithmes élaborés. Il n'est donc pas possible de simplement calculer les deux nuages de facettes associés à chacun des deux couples (branche mère, branche fille), de réunir ces deux ensembles et ensuite de trier en Z les facettes pour les dessiner dans l'ordre. Il convient de dessiner (et donc de trier) d'abord l'un des deux ensembles de facettes (celui qui correspond à la branche la plus profonde à l'écran) et seulement ensuite l'autre : le tri des facettes d'un branchement est ainsi à nouveau décomposé en deux sous-tris indépendants. On dessine d'abord la branche la plus profonde à l'écran puis ensuite l'autre.
L'algorithme réalisant cette opération pour un branchement quelconque est décrit par la procédure DESSINER_BRANCHEMENT ci-après.
"cône" et "ensemble de facettes" sont des structures de données permettant le stockage mémoire de toutes les informations décrivant respectivement un cône courbé et un ensemble de facettes quadrangulaires. La fonction CONE_AVANT (respectivement CONE_ARRIERE) rend le cône de z maximum (respectivement minimum) du branchement passé en paramètre. CALCULER_FACETTES est la fonction qui calcule l'ensemble des facettes de modélisation d'un cône courbé. SUPPRIMER_FACETTES_INCLUSES est une procédure à deux paramètres, un ensemble de facettes E et un cône courbé C, qui supprime de l'ensemble de facettes E toutes celles dont les quatre sommets sont à l'intérieur du cône C. SUPPRIMER_FACETTES_COMMUNES est une procédure à deux paramètres, un ensemble de facettes E et un cône courbé C, qui supprime de l'ensemble de facettes E toutes celles qui sont communes (très proches) du cône C (appliqué dans le cas d'une fourche). Enfin, DESSINER_ENSEMBLE_FACETTE est la procédure qui prend en charge le dessin d'un ensemble de facettes quadrangulaires planes ne se recoupant que sur leurs bords.
Procedure DESSINER_BRANCHEMENT(BRANCHEMENT : branchement)
CONE_AVANT, CONE_ARRIERE : cône ;
ENSEMBLE_DROIT, ENSEMBLE_GAUCHE : ensemble de facettes ;
Debut
CONE_AVANT <- CONE_AVANT(BRANCHEMENT) ;
CONE_ARRIERE <- CONE_ARRIERE(BRANCHEMENT) ;
ENSEMBLE_AVANT <- CALCULER_FACETTES(CONE_AVANT) ;
ENSEMBLE_ARRIERE <- CALCULER_FACETTES(CONE_ARRIERE) ;
Si BRANCHEMENT n'est pas une fourche alors
si EPAISSEUR(CONE_AVANT) > EPAISSEUR(CONE_ARRIERE) alors
SUPPRIMER_FACETTES_INCLUSES(ENSEMBLE_ARRIERE,CONE_AVANT) ;
sinon
SUPPRIMER_FACETTES_INCLUSES(ENSEMBLE_AVANT,CONE_ARRIERE) ;
fin_si
sinon
SUPPRIMER_FACETTES_COMMUNES(ENSEMBLE_ARRIERE,CONE_AVANT) ;
fin_si
DESSINER_ENSEMBLE_FACETTE(ENSEMBLE_ARRIERE) ;
DESSINER_ENSEMBLE_FACETTE(ENSEMBLE_AVANT) ;
fin_proc
Une dernière simplification possible consiste à supprimer toutes les facettes qui ont une normale extérieure à l'objet en z négatif en coordonnées écran (voir photographie 7E et planche 5). En effet, toutes ces facettes seront obligatoirement recouvertes par d'autres qui auront une normale en z positive. Par cette simplification le nombre de facettes à dessiner est approximativement divisé par 2.
Toutes les facettes supprimées en cours de modélisation d'un branchement le seront avant le tri en z de manière à accélérer au maximum cette phase critique.
Ces transformations de la technique de dessin apportent un triple avantage :
- elles diminuent le nombre de facettes réellement dessinées (elles sont calculées, mais pas triées et affichées).
- les ensembles de facettes à trier sont toujours plus petits. Même s'il sont plus nombreux, le temps de calcul global est diminué.
- Le problème du recoupement des facettes n'existe plus. Les erreurs commises sont suffisamment peu marquées pour être masquées. Après la phase de calcul des éclairages elles deviennent alors virtuellement invisibles. On peut d'en rendre compte sur la photographie 7E et la planche 5 qui présentent un branchement en gros plan.
7.3.6 Calcul d'un éclairage pour chacune des facettes
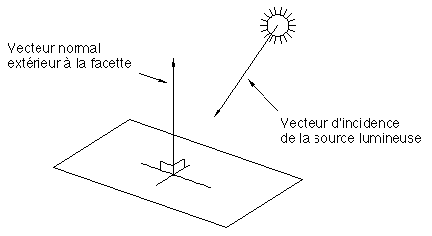
Figure 7P : Paramètres de calcul d'un éclairage
La réalisation d'un éclairage sur une facette plane est un problème classique de l'informatique graphique. Connaissant le vecteur normal à la facette, extérieur à l'objet modélisé (vecteur déjà calculé par ailleurs) ainsi que le vecteur normé donnant la direction d'incidence des rayons solaires (une seule source d'éclairage dans ce cas), il est possible de calculer la réflexion diffuse par la facette par la classique formule de Lambert (en fonction du cosinus de l'angle de ces deux vecteurs, Figure 7P). Un terme d'illumination ambiante est alors ajouté. En tenant compte de la teinte propre de la facette on calcule la couleur réelle d'affichage.
7.3.7 Calcul des ombres portées à l'intérieur d'un arbre
Une des caractéristiques visuelles permettant de bien appréhender la géométrie d'un arbre est le jeu de la lumière et des ombres qui apparaissent en son sein sous l'action d'un éclairage. Dans ce paragraphe, nous décrivons une méthode permettant de calculer les ombres portées des branches les unes sur les autres.
Le calcul de l'ombre du feuillage (voir paragraphe 7.4) est effectué statistiquement en dessinant sur chaque branche matérialisant une arête de l'arbre un certain nombre de polygones matérialisant des feuilles selon les mêmes lois de placement que celles décrites au paragraphe 7.4.2. A ce niveau l'arbre est donc modélisé par un ensemble de facettes pour les branches et de polygones pour les feuilles.
L'opération de dessin de l'arborescence va être précédée d'un traitement préalable consistant à réaliser un Z-Buffer de calcul des ombres portées. C'est à dire :
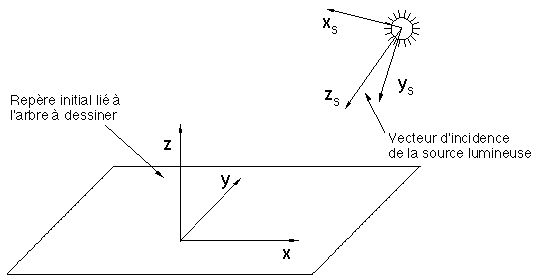
Figure 7Q : Changement de repère pour le Z-Buffer de calcul des ombres portées
1) On opère sur l'arborescence un changement de repère de telle manière que l'axe des z deviennent la direction d'incidence du soleil (les orientations de l'axe des x et de l'axe des y peuvent être quelconques pourvu que le repère reste orthonormé) et que tout point de l'arbre puisse être dessiné dans un plan image de dimension finie appelé zone de mémoire du Z-Buffer (Figure 7Q).
2) On dessine l'arbre dans ce repère au moyen d'un algorithme du Z-Buffer mettant en œuvre une décomposition de l'arborescence en facettes géométriques triangulaires et rectangulaires similaire à celle du paragraphe 7.2 (affichage 2D d'un arbre) pour les coordonnées x et y, mais incluant en plus la coordonnée z pour obtenir des triangles et des rectangles dans
R3. Par calcul de ces facettes au cours du parcours de l'arbre, par leur décomposition en pixels, et par comparaison d'altitude vis à vis de l'altitude de ce qui a déjà été traité, on établit dans la zone mémoire du Z-Buffer une carte de l'altitude des points effectivement éclairés par le soleil dans l'arbre.
Photographie 7F : Ombres portées à l'intérieur d'un arbre avec feuillage, le soleil est bas sur l'horizon à gauche (contraste renforcé de l'image).
3) Lors du dessin effectif de l'arborescence, il sera possible, au moyen du même changement de repère que dans 1), de calculer un triplet de coordonnées (x,y,z) dans le repère lié au soleil pour chaque point affiché. Si la coordonnée z dans ce repère de ce point est plus grande celle du point PZB de la zone de mémoire du Z-buffer, alors on est certain que ce point est à l'ombre d'un autre point.
Remarques:
- L'utilisation d'un tel algorithme sur un micro-ordinateur n'est possible que si la zone de mémoire du Z-Buffer n'est pas trop volumineuse. Dans notre implantation, les résultats sont satisfaisants avec une zone de 256 x 256 points. Plus la mémoire Z-Buffer est grande, meilleure est la précision du calcul de l'ombre.
- Les feuilles réelles de l'arbre ont été remplacées lors du calcul des ombres par des polygones (rectangles) afin de simplifier les calculs. L'ombre obtenue l'est ainsi de façon "statistique". Comme toute méthode statistique, elle ne devient réellement valable que si elle porte sur un nombre important d'éléments, on devra donc afficher des arbres avec beaucoup de feuilles (Photographie 7F, planche 7B).
7.3.8 Plaquage d'une texture
L'obtention d'un rendu réaliste requiert un plaquage de texture sur les branches (Photographie 7G). Cette contrainte devient particulièrement importante pour un dessin en gros plan (Photographies 7E et 7L, planches 5 et 10). Chaque facette dessinée devra être traitée de manière à casser l'uniformité de sa teinte.

Photographie 7G : Arbre 3D avec texture et sans texture.
Le but n'est pas ici de décrire des algorithmes d'ordres généraux sur le plaquage de texture. La technique employée permet de dessiner des lignes aléatoirement tiretées dans l'axe de la facette à traiter (axe de la branche connu implicitement au cours de la modélisation pour le dessin). Les divers paramètres définissables sont la longueur moyenne des tirets, leur épaisseur, leur intensité lumineuse vis à vis de celle de la facette. Le choix des extrémités de ces lignes est grandement facilité par le fait qu'on peut considérer que toutes les facettes sont des parallélogrammes, un simple algorithme de Bresenham permet le parcours simultané des deux bords opposés d'une facette pour calculer les extrémités des segments (qui joignent les deux bords opposés de la facette) aléatoirement tiretés à tracer (Figure 7R). Une évolution du même algorithme de Bresenham permet par ailleurs de réaliser le segment tireté.
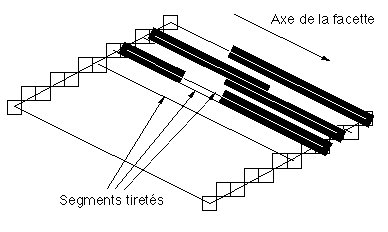
Figure 7R : Plaquage d'une texture
7.4 Les feuilles
Un aspect essentiel manque au dessin des arbres tel qu'il a été décrit jusqu'à présent : les feuilles. Nous définissons ci-après un modèle de dessin de feuilles permettant d'obtenir un dessin réaliste d'arbres munis d'un feuillage (Planches 2A, 2B, 7, 8, 9,…). Un algorithme efficace et rapide est nécessaire pour dessiner des arbres avec des centaines ou des milliers de branches et donc un feuillage de plusieurs milliers de feuilles.
Une méthode pour créer des feuilles à travers un phénomène de croissance a été donnée par Prusinkiewicz et al. [PL88]. Notre modèle se distingue de celui de Lienhardt et Françon [Li87], [LF87] par l'utilisation de structures combinatoires arborescentes au lieu de cartes planaires. La méthode proposée par Bloomenthal [Bl85] autorise la visualisation et le positionnement d'une feuille digitalisée (une feuille d'érable) avec l'aide d'une structure polygonale pour la simulation 3D. La méthode est différente de la notre : son but n'est pas de proposer un modèle général. D'autres approches fractales apparaissent, comme chez Oppenheimer [Op86] où la limite extérieure de la forme de la feuille est la limite d'une croissance fractale récursive des nervures internes, et chez Demko et al. [DH85] qui génèrent des feuilles considérées comme des structures fractales, en utilisant des "systèmes de fonctions itérées".
7.4.1 Modèle de dessin des feuilles
Comme le montre la figure 7S, une feuille est composée d’une arborescence de nervures plongée dans le limbe (corps de la feuille quand les nervures ont été retirées). En première approximation cette arborescence est un arbre ternaire à l’exception de la queue de la feuille (ou pétiole) où l’arité peut prendre toute valeur impaire. Par la suite, nous appellerons nervure principale une séquence d’arêtes centrales issue du pétiole, et nervure secondaire une arête issue d’une nervure principale. Nous considérerons qu’il n’existe pas de nervure plus profonde que secondaire à l'intérieur d'une feuille. Un lobe est constitué d’une nervure principale, de toutes les nervures secondaires qui s’y rattachent et du bord délimitant la part de limbe associé à cette nervure (bord dont la géométrie n’est pas spécifiée à ce niveau).
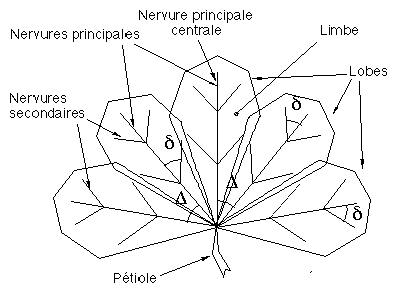
Figure 7S : Géométrie de la feuille
La structure topologique de la feuille est alors définie par :
- le nombre de lobes,
- la "taille" de la feuille, donnée par le nombre n de nœuds sur la nervure principale centrale. Le nombre de nœuds des autres nervures principales est une fonction discrète (usuellement décroissante) de n et de la "distance" (nombre de lobes) entre cette nervure principale et la nervure principale centrale.
La structure géométrique est obtenue en définissant :
- la position des nœuds à l’aide de 3 paramètres (Figure 7S) : deux angles
d et ? et une loi de longueur L pour les arêtes de l’arborescence. ? est l’angle entre deux nervures principales successives, et d est l’angle entre une nervure secondaire et la nervure principale qui lui donne naissance. La longueur L(d) d’une arête est une fonction croissante de la "profondeur" d de l’arête (d est la distance comptée en nombre d’arêtes entre l’arête considérée et l'arête terminale du lobe). Trois lois ont été testées :(1) L(d) = Cte, (2) L(d) = A * d + B, (3) L(d) = A * Log(1 + d)+ B.
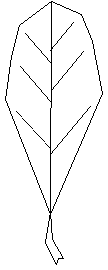
Figure 7T : Décrochement géométrique des nervures secondaires
Une incertitude paramétrable peut être appliquée à ces lois de longueur de manière à ne jamais généré de feuilles strictement identiques.
- le bord de chaque lobe comme un polygone joignant la racine et les points déterminés par les extrémités des nervures secondaires dépendant de ce lobe.
- L'importance du décrochement entre la nervure droite et la nervure gauche à chaque nœud de nervure principale (Figure 7T). Ce décrochement est purement géométrique, un double jeu de coordonnées est conservé pour chaque nœud de nervure principale.
Le bord du limbe est le polygone joignant les morceaux du bord de chaque lobe qui appartiennent au bord du limbe (Figures 7S et 7T). Cette représentation polygonale est suffisante quand les feuilles sont tracées avec une petite taille (vue de loin), elle permet le dessin rapide d’un arbre avec son feuillage même s'il est composé de plusieurs milliers de feuilles. Par paramètrage des trois coefficients
D, d et L, du nombre de lobes et de leur taille on obtient une grande variété de formes (Photographie 7H, planche 11A).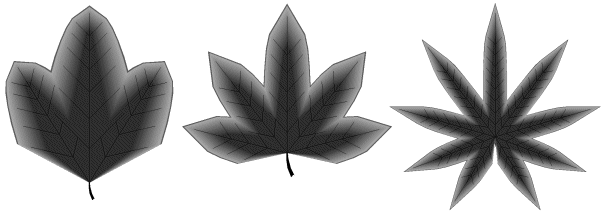
Photographie 7H : Influence de la topologie et de la géométrie sur la forme d'une feuille

Photographie 7I : Dégradé sur le limbe d'une feuille
Dans le feuillage d’un arbre, les feuilles se recouvrent les unes les autres. Pour obtenir un feuillage contrasté, il est nécessaire de distinguer les feuilles par des teintes différentes. Un aspect très réaliste est obtenu en générant un dégradé de couleurs sur le limbe (Photographie 7I et planches 11). Dans ce but, chaque zone d'un dégradé de couleurs de lobe est obtenue par combinaison de deux transformations géométriques:
- une homothétie dont le centre est la racine de la feuille.
- une affinité d’axe la nervure principale, de direction les nervures secondaires à droite pour la partie droite du lobe, à gauche pour la partie gauche du lobe et de rapport compris entre 0 et 1.
Quand une feuille réaliste est nécessaire, en particulier pour un gros plan, le bord du limbe doit être lissé (Photographie 7J, planches 11). Cette opération est réalisée par interpolation au moyen de morceaux de fonctions cubiques remplaçant chacun des segments du bord polygonal. Chaque morceau de cubique est défini par les deux extrémités du segment associé et par deux tangentes en ces points.
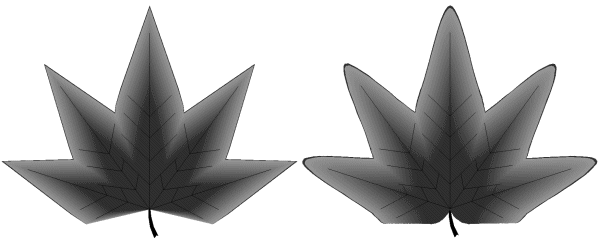
Photographie 7J : Feuille non lissée (à gauche) et feuille lissée (à droite).
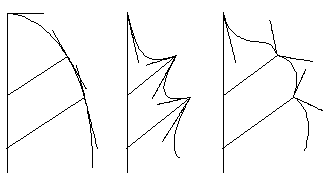
Figure 7U : Différents types de bords de limbe
L'orientation de ces tangentes permet d'obtenir un bord rigoureusement lisse si elles sont colinéaires de chaque côté d'un sommet du limbe (Photographie 7J et planche 11B bas). Il est aussi possible de générer des dentelures ou des boursouflures sur le limbe en créant un angle entre ces tangentes (Figure 7U, Photographie 7K).

Photographie 7K : Feuille sans (à gauche) et avec (à droite) Indentation de son bord.
7.4.2 Placement des feuilles
Il n’est pas possible de générer une feuille totalement différente à chaque fois qu’on en dessine une dans l’arbre. La représentation géométrique d'une seule feuille est conservée comme référence en mémoire. Une nouvelle représentation est calculée à chaque fois qu'on veut dessiner une feuille sur une branche en effectuant une rotation par rapport au trois axes ainsi qu'une homothétie (Photographie 7L). Un choix aléatoire dans un ensemble fini de palettes prédéfinies pour le dégradé de la feuille est également opéré. Par ces rotations et homothéties de valeurs aléatoires, par ce choix de palette aléatoire, la feuille réellement dessinée est à chaque fois différente tout en représentant le même objet. Le paramètrage de la rotation de la feuille suivant les trois axes permet l'obtention éventuelle d'effets spéciaux tels que le vent ou la gravité. Le paramètrage de la taille de la feuille permet la simulation de différentes étapes de croissance au cours d'une même année (Photographie 7M).

Photographie 7L : Une branche en gros plan
Le nombre de feuilles placées sur l’arbre est calculé au moyen d'une loi dépendant de l’ordre (Strahler ou évolution) de la branche traitée. Les feuilles sont par exemple implantées stochastiquement avec une grande densité sur les branches de petits ordres de Strahler et une densité nulle pour les branches d’ordres de Strahler importants (Photographie 7M).
7.4.3 Conclusion
Comme dans la méthode de génération des arbres binaires par matrice de ramification, cet algorithme de dessin de feuilles sépare la croissance historique de la feuille et la topologie, celle-ci étant le caractère principal dont est issue la géométrie. La simplicité de la structure sous-jacente (un arbre) et des calculs géométriques autorise un algorithme de génération et de dessin très rapide issu d’une modélisation facile de la topologie, tout en obtenant une grande diversité de formes (Photographies 7H, 7I et 7J). Des feuillages variés et touffus peuvent donc être générés.
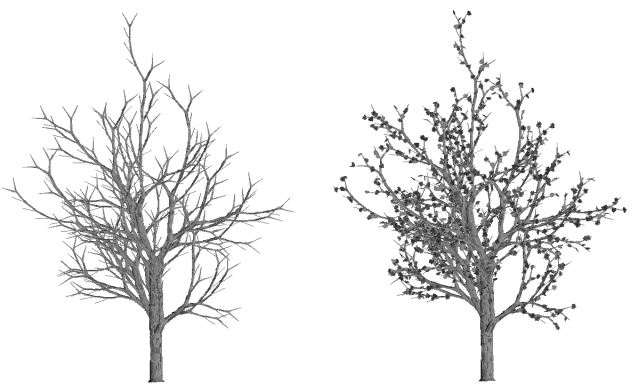

Photographie 7L : Un arbre à différentes étapes de développement de son feuillage.
7.5 Conclusion
La technique de dessin 2D décrite en début de chapitre possède l’avantage d’être particulièrement rapide. Elle permettra généralement d’obtenir un "aperçu avant dessin définitif" d’un arbre de taille importante ou bien un dessin définitif d’un arbre vu de très loin. Une autre raison d’être de cet algorithme est qu’il permet très bien l’analyse topologique d’une arborescence.
Le modèle de dessin 3D développé dans la deuxième partie de ce chapitre permet l'obtention d'images très réalistes par l'utilisation d'une représentation volumique des branches, la définition d’une texture et l'introduction d'un modèle de dessin de feuilles végétales. Ces algorithmes ont été conçus de manière à être suffisamment rapides pour permettre la réalisation de dessins dans des temps assez courts (voir annexe A1) sur micro-ordinateur. Une grande part des techniques qui sont utilisées pour accélérer le dessin peuvent être adaptées dans le cas d'un dessin sur station de travail graphique de manière à obtenir des dessins encore plus rapides et réalistes. En particulier la technique de décomposition en branchements peut être conservée (et probablement améliorée). Les approximations de calcul et d'affichage qui ont été consenties en contre-partie de l’obtention de bonnes performances ne nuisent qu'assez peu à la qualité finale dans la mesure où l'on ne désire réaliser que des images fixes. Dans le cas où une animation doit être construite (pour tourner autour d'un arbre ou montrer une croissance régulière sur plusieurs années par exemple), on préférera alors un dessin global de l'arbre sans décomposition en branchements, dessin qui ne pourra alors être effectué que sur une station graphique performante.