Chapitre 8
Algorithmes et techniques de rendu
des reliefs et bassins fluviaux
8 Algorithmes et techniques de rendu des reliefs et bassins fluviaux
8.1 Introduction
On suppose disposer d’une carte planaire quasi-triangulaire plongée dans
R3 modélisant un relief (cf chapitre 6). Ce chapitre décrit les algorithmes utilisés pour dessiner cette carte de manière à obtenir un dessin réaliste. Une technique de base classique (le Z-buffer) est développée de manière à être adaptée au cas particulier de notre modèle de relief, de façon à rendre possible et rapide (quelques minutes, voir annexe 1) sur un ordinateur de faible puissance (quelques MIPS et MFlops) le dessin réaliste de cartes comportant plusieurs milliers de facettes.Différents effets visuels comme une stratification des couleurs fonction de l’altitude, l’apparition de la rivière sous-jacente ou une visualisation prononcée des lignes de crêtes sont possibles. On verra aussi comment réaliser de manière rapide l’affichage d’un relief avec éventuellement plusieurs milliers d’arbres (modèle des chapitres 3, 4 et 7) à l’intérieur.
8.2 Dessin des montagnes
8.2.1 Choix d'une méthode d'élimination des parties cachées
Contrairement au dessin des branchements où le nombre de facettes à traiter simultanément n'était pas très important, le dessin de la carte matérialisant une montagne peut nécessiter la gestion de plusieurs milliers, voir plusieurs dizaines de milliers de facettes triangulaires. L'utilisation d'un algorithme de tri n'est plus envisageable dans ce cas.
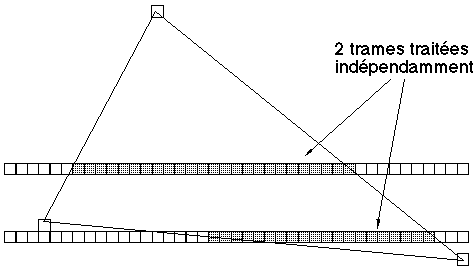
Figure 8A : Z-Buffer par trame
La technique adoptée est un algorithme du Z-Buffer par trame (Figure 8A). En effet cette méthode est relativement bien adaptée à une utilisation sur micro-ordinateur car elle minimise la quantité de mémoire utilisée, au prix toutefois d'un surcoût en terme de calculs. La technique classique du Z-Buffer consiste à parcourir séquentiellement l'ensemble de facettes à afficher, à décomposer chacune de ces facettes en un ensemble de points positionnés dans
N3 et, par utilisation de deux tableaux ALTI (donnant la coordonnée z des pixels) et COUL (donnant la couleur des pixels) dimensionnés au nombre de pixels de l'écran, construire l'image finale par comparaison des ALTI des points des facettes déjà affichées et des points de la facette en cours de traitement.La différence entre un Z-Buffer classique et un Z-Buffer par trame est que l'image n'est plus traitée globalement, mais décomposée en un ensemble de lignes horizontales (ou verticales) pouvant être traitées indépendamment les unes des autres (ici séquentiellement). Chaque facette sera donc analysée pour chaque ligne. Un prétraitement permet de déterminer les lignes minimum et maximum intersectant la facette et de tenir ainsi dynamiquement à jour au cours de l'algorithme, la liste des facettes actives pour la ligne courante.
Cet algorithme peut être décrit comme suit :
Réserver deux tableaux d'entiers ALTI et COUL de dimension la résolution en x de l'écran
/* ALTI pour l'altitude courante maximale,
COUL pour la couleur courante de dessin */
Calculer les coordonnées écran de chacun des polygones
Pour chaque LIGNE de l'écran
Initialiser ALTI à -8 et COUL à la couleur de fond
Pour chaque FACETTE intersectant la LIGNE
Pour chaque POINT de l'intersection
Si Z(FACETTE,LIGNE,POINT) > ALTI[POINT] alors
ALTI[POINT] = Z(FACETTE,LIGNE,POINT)
COUL[POINT] = COULEUR(FACETTE)
Fin_si
Fin_pour
Fin_pour
afficher tous les POINTs de la LIGNE avec la couleur COUL[POINT]
Fin_pour
Z(FACETTE,ligne,point) est une fonction qui calcule la coordonnée en z (profondeur écran) du point de coordonnées écran (POINT,LIGNE) du polygone FACETTE. COULEUR est une fonction qui permet de calculer la couleur d'affichage d'un polygone quelconque (voir paragraphes suivants).
Cette méthode est très économe en mémoire, en effet seuls deux tableaux de quelques milliers d'octets sont nécessaires. En revanche, la quantité de calcul à effectuer est assez importante (en particulier pour déterminer les points d'intersection d'un polygone et d'une ligne et leurs altitudes). Par rapport à un Z-buffer classique, un certain nombre de calculs (pour la décomposition des facettes en lignes) sont effectués plusieurs fois, pour toutes les trames intersectant un polygone quelconque. Il s'ensuit une perte de temps largement compensée par le fait que la quantité de mémoire nécessaire à l'implémentation d'un tel Z-Buffer aurait été réellement trop importante pour un micro-ordinateur (gestion globale de l'écran et non plus seulement ligne par ligne).
8.2.3 Rendu réaliste
L'algorithme du Z-buffer ne permet que le masquage des faces cachées, il ne permet en aucun cas de réaliser un rendu réaliste (Photographie 8A). Un certain nombre de techniques supplémentaires doivent être mises en œuvre. C'est à dire de manière non exhaustive :
- la gestion d'un éclairage (Paragraphe 8.2.3.1),
- la gestion d'un lissage (Paragraphe 8.2.3.2),
- la gestion d'un plaquage de texture (Paragraphe 8.2.3.3), voire d'une végétation (Chapitres 3, 4, 7 et paragraphe 8.3),
- la gestion de l'affichage des rivières (Paragraphe 8.2.3.4).
8.2.3.1 La gestion d'un éclairage sur les facettes
La technique de calcul de l'éclairage des facettes est la même que celle abordée au paragraphe 7.3.6. A partir de la carte pointée topologique et de son plongement géométrique, on peut déterminer le vecteur normal, extérieur au relief, à chacune des facettes et par produit scalaire avec le vecteur normé éclairage obtenir la composante lumineuse de la couleur de la facette (Photographie 8A, planche 14A).
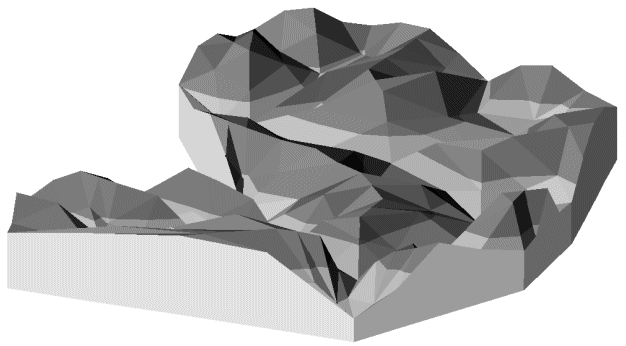
Photographie 8A : Z-Buffer d'affichage avec éclairage des facettes
8.2.3.2 La gestion d'un lissage
La modélisation par facette plane se heurte à un gros problème de réalisme si les facettes affichées à l'écran sont de surfaces importantes. La réalisation d'un lissage est impérative pour obtenir un haut degré de réalisme. Ce lissage est déjà amorcé par les différentes retriangularisations successives qui permettent, en multipliant le nombre de facettes, de rendre la carte de plus en plus précise, la taille moyenne des facettes étant de plus en plus petite. Cette technique est toutefois vouée à l'échec si un certain nombre de facettes doivent être représentées à l'écran en gros plan.
Plutôt que de réaliser un lissage par multiplication des facettes de la carte - opération qui alourdirait considérablement la gestion de la structure de données topologique et donc la quantité de calcul à effectuer - nous proposons d'implanter un lissage sur les couleurs du type de celui initié par Gouraud (cf [Go71]).
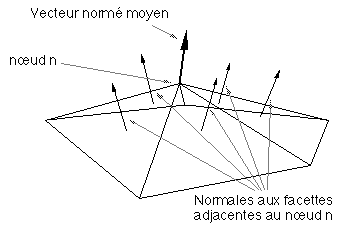
Figure 8B : Normales pour un ombrage de Gouraud
La technique consiste à calculer la composante lumineuse à attribuer à chacun des pixels de la facette à représenter. Pour Gouraud cette composante est obtenue par interpolation linéaire entre les trois valeurs des composantes lumineuses attribuées aux sommets de la facette. Cette composante - attribuée à chacun des sommets de la carte - est calculée par produit scalaire du vecteur moyenne de tous les vecteurs unitaires normaux aux facettes adjacentes au nœud considéré, avec le vecteur normé éclairage (Figure 8B, photographie 8B, planche 14B).

Photographie 8B : Ombrage de Gouraud sur un relief
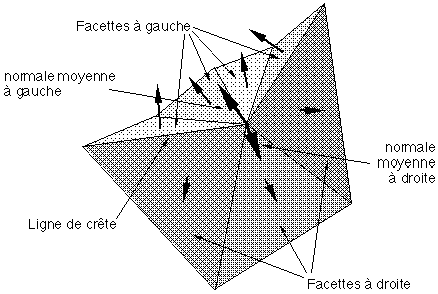
Figure 8C : Matérialisation des lignes de crête
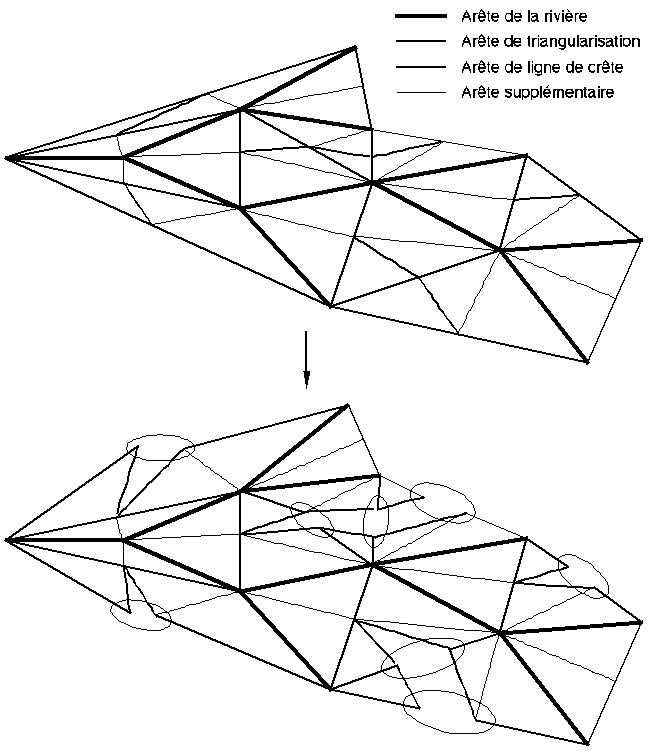
Figure 8D : Séparation de la carte selon les lignes de crête
Un autre type de lissage sur les couleurs à été imaginé par Phong (cf [Ph75]) où l'interpolation linéaire est effectuée sur des vecteurs normés moyens associés aux sommets plutôt que sur des luminosités en valeur numérique. Cette technique n'a pas été implantée car elle est considérablement plus gourmande en temps CPU que celle de Gouraud, le gain de qualité attendu ne se justifie pas dans le cas particulier du dessin de relief.
L'intérêt du lissage de Gouraud est qu'il permet de rendre invisible la limite entre les facettes adjacentes en jouant sur les couleurs des points affichés. Il réalise ainsi un lissage sans avoir à gérer de facettes supplémentaires.
Le relief, s'il reste apparent par un "moutonnement" de la luminosité intrinsèque des facettes, est très atténué, donnant l'impression de voir des collines plutôt que des montagnes. Si l'on considère l'atténuation du relief provoquée par le lissage de Gouraud trop importante, une solution intermédiaire consiste à affecter deux composantes lumineuses à chacun des sommets des lignes de crêtes, une valeur pour un côté de la ligne de crête et une autre valeur pour l'autre côté (Figure 8C). Ces deux couleurs sont calculées à partir des deux ensembles de normales correspondant aux deux ensembles de facettes situés de chaque côté de la ligne de crête (Photographie 8C, planche 15 et 16).
Au niveau topologique cette opération est équivalente à celle consistant à séparer la carte selon chaque arête ligne de crête par dédoublement de cette arête (Figure 8D).
8.2.3.3 Le texturage
Pour obtenir un rendu plus réaliste un plaquage de texture sur les facettes doit encore être réalisé. L'attribution d'une teinte de base fonction de l'altitude du point dessiné et éventuellement de l'orientation de la facette permet la simulation des différentes strates de végétation ou de couleur susceptibles d'apparaître dans un relief. L'altitude de chacun des points affichés est aisément calculable au cours de la phase de réalisation du Z-Buffer. La teinte de tout point peut donc être paramétrée si l'altitude maximale du relief est connue (voir toutes les photographies présentées jusqu'à présent et les planches 15 et suivantes).

Photographie 8C : Matérialisation des lignes de crête à partir du lissage des couleurs
La réalisation d'un plaquage de texture au sens communément entendu en informatique graphique ne sera pas abordée ici car le réalisme obtenu est suffisant à ce niveau de rendu.
De plus, l'utilisation de ces reliefs a pour but la réalisation de paysages incluant une végétation et plus particulièrement des arbres, un texturage fin du sol risque fort d'être masqué par la végétation qui doit venir se placer par dessus (Paragraphe 8.3).
8.2.3.4 Les rivières
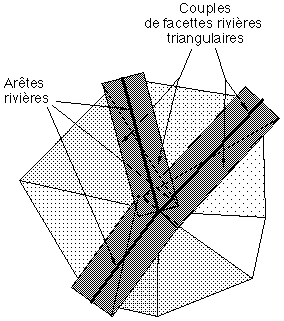
Figure 8E : Création des facettes rivière
Le problème de l'affichage des rivières n'a pas été abordé jusqu'à présent. Pour conserver l'unité de la méthode d'affichage choisie (Z-buffer), les fleuves devront être gérés comme des facettes. L'ensemble de ces facettes sera calculé à partir de la carte topologique plongée dans
R3. Chaque arête rivière sera modélisée par 2 facettes triangulaires situées géométriquement légèrement au dessus du relief (Figure 8E). Les problèmes de recollement au niveau des nœuds sont ignorés car ils sont négligeables. Le fait que des facettes rivières puissent couper des facettes de la carte n'est pas non plus problématique car l'algorithme du Z-buffer ne génère pas d'erreurs dans ce cas, les rivières n'en apparaîtront que plus réalistes car moins linéaires (Photographie 8D, planche 16).On paramètre facilement la largeur des rivières en fonction des ordres attribués aux arêtes au cours du calcul de la géométrie de la carte.
La gestion des rivières par modification directe de la carte pour introduire ces facettes au niveau topologique aurait pu être effectuée, toutefois, elle conduit à d'importants problèmes de recollement aux nœuds, problèmes tant topologiques que géométriques.

Relief sans rivière

Relief avec rivières
Photographies 8D : Matérialisation des rivières
8.3 Réalisation de paysage par introduction d'arbres dans un relief
La création d'un paysage réaliste et a fortiori l'affichage de son évolution au cours du temps nécessite l'introduction d'arbres dans un relief. Comme il a été précisé au chapitre 7, il n'y a pas modélisation globale d'un arbre au moyen d'un nuage de facettes. Il n'est donc pas possible de construire l'ensemble de facettes représentant un relief muni de ses arbres. Il apparaît de toute façon que la taille d'un tel ensemble serait irréaliste vis à vis des capacités d'un micro-ordinateur (plusieurs dizaines de millions de facettes pour un paysage avec plusieurs centaines d'arbres). La méthode proposée ci-après est satisfaisante dans une majorité des cas (Planches 18 à 21). Les temps d'affichage restent inférieurs à l'heure pour une image compliquée (plusieurs centaines d'arbres).
Le principe de la méthode consiste à gérer des images rectangulaires d'arbres comme des facettes rectangulaires au cours du Z-Buffer d'affichage (Figure 8G). La taille de ces images devra être adaptée pour correspondre à la taille réelle voulue à l'écran, c'est à dire subir un zoom pour adapter la taille de l'arbre à la taille du relief et un écrasement suivant l'axe y pour tenir compte de l'inclinaison relative entre le repère local au relief et le repère de l'observateur (Figure 8F).
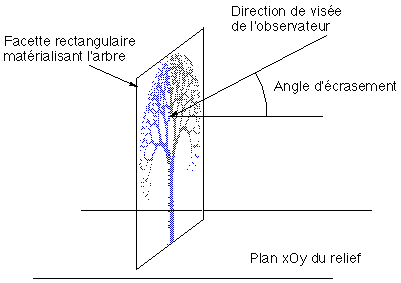
Figure 8F : Opération sur une facette arbre
La méthode employée pour effectuer ces opérations pourra être :
- le dessin direct à la bonne taille d'un arbre dont la topologie et la géométrie sont préalablement stockées en mémoire,
- le zoom sur une image conçue auparavant.
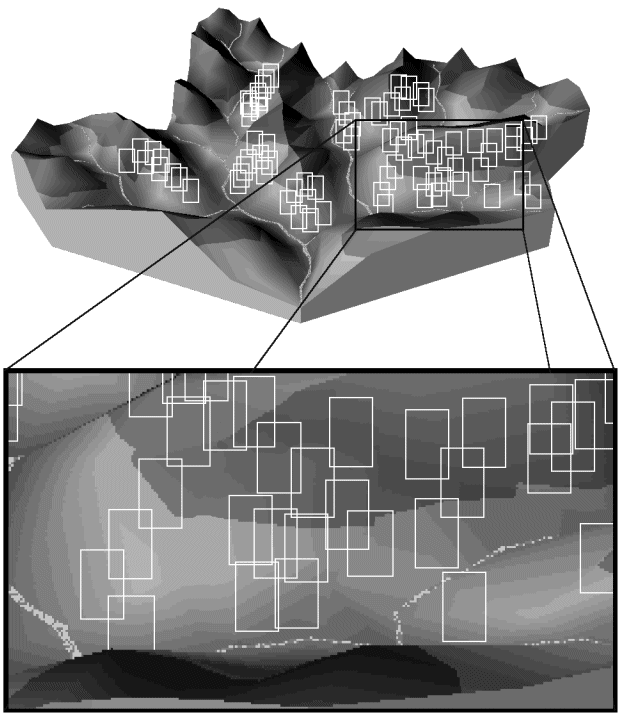
Figure 8G : Introduction d'arbres dans un relief
Une image (rectangulaire avec fond) d'arbre affichée devra bien entendu voir sa couleur de fond supprimée de manière à laisser apparaître les arbres ou le relief en arrière-plan.
Cette méthode de dessin permet l'obtention de résultats réalistes avec éventuellement la présence d'arbres en gros-plan à l'écran suivant la position de l'observateur (planches 18 à 21). Une limitation d'utilisation de cette technique est que l'inclinaison relative entre le relief et l'observateur ne doit pas être trop importante. Elle ne permet donc pas la réalisation de dessins de la végétation vue du zénith.
Pour automatiser le travail de conception et d'affichage d'une scène, une bonne méthode consiste à construire un fichier scène contenant toutes les informations nécessaires à la réalisation du paysage (voir paragraphe A1.6), c'est à dire :
- le fichier contenant le relief
- les informations nécessaires au dessin de ce relief (teintes de base, position du soleil, position de l'observateur, direction de visée de l'observateur, ...)
- pour chacun des arbres à afficher dans le relief :
¡
sa position dans le plan, ce qui permet de calculer son altitude en utilisant la carte et donc de fixer parfaitement la position de la facette image à prendre en compte,¡
le type d'image à reconstruire et les informations nécessaires à sa construction éventuelle (un fichier arbre si l'image utilisée est à dessiner à la bonne taille ou un fichier image à zoomer).
Relief vu de loin (les arbres affichés sont ceux dont la place est définie à la figure 8G).

Relief avec fleuve et petits arbres en arrière-plan, nuage fractal dans le ciel (cf chapitre 1), arbre et branches d'arbres en avant-plan
Photographies 8E : Reliefs avec arbres
8.4 Conclusion
Les algorithmes utilisés dans ce chapitre pour la représentation des reliefs sont très classiques en informatique graphique. Leur adaptation à notre problème particulier permet d'obtenir des résultats de bonne qualité. La réalisation d'images de reliefs sans arbre est tout à fait possible sur un micro-ordinateur dans des temps acceptables (Quelques minutes, voir annexe A1).
L'incorporation d'arbres devient en revanche une lourde tâche en raison de la quantité de calcul supplémentaire assurée par la machine pour la gestion des facettes images d'arbres. Les temps de calcul peuvent être considérablement allongés si l'on désire constituer de véritables forêts (Quelques dizaines de minutes, voir annexe A1), mais il n'y a pas de réelle limitation dans le nombre d'arbres qu'il est possible d'inclure (plusieurs milliers). La constitution de fichiers scènes permet de réaliser très facilement des animations comme par exemple des déplacements à l'intérieur d'un relief (cf animation "Survol" et la planche 19), ou plus simplement l'obtention d'images d'un relief vues de positions différentes (planches 18, 20 et 21).