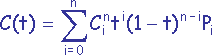Examen de TD n°2 2005-2006
![]()
On n'oubliera pas de fournir quelques explications sur les techniques employées.
Question 1: Caméras en OpenGL
| On
considère les lignes de code OpenGL ci-contre :
a) Décrire ce que réalisent ces lignes de code. b) Cela semble-t-il cohérent (réponse à justifier) ? |
glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluPerspective(20.0F,2.0F, 140.0F,160.0F); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); gluLookAt(100.0F,50.0F,100.0F, 0.0F,0.0F,0.0F, 1.0F,0.0F,0.0F); glutWireSphere(30.0F,72,72); |
Décrire une technique de calcul permettant de tester si ce polygone est plan ou non (ne pas implanter).
b) On considère un polygone plan défini dans un espace à trois dimensions.
Décrire une technique de calcul permettant de tester si ce polygone est de bord convexe ou non (ne pas implanter).
Question 3: Courbes lissées
On considère n+1 points Pi (0 <= i <= n) d’un espace à trois dimensions.| Soit l’équation C(t) de calcul des courbes de
Bézier : t compris entre 0 et 1, |
Rappels:
|
Ecrire une fonction de calcul d’une courbe de Bézier sur une ligne polygonale de n+1 points avec m sommets de discrétisation uniformément répartis sur l’intervalle [0,1].
Question 4: Algorithmique
| On
considère l’algorithme ci-contre :
Il s’agit de l’algorithme de Bresenham pour le dessin de segments de droite ((xi,yi)-(xf,yf)) en 8-connexité (chaque pixel possède 8 voisins : en haut, en bas, à droite, à gauche, en haut à droite, en haut à gauche, en bas à droite, en bas à gauche) .
|
void ligne(int xi,int yi, int xf,int yf) { int dx,dy,cumul,x,y ; x = xi ; y = yi ; dx = xf - xi ; dy = yf - yi ; allume_pixel(x,y) ; cumul = dx / 2 ; for ( x = xi+1 ; x <= xf ; x++ ) { cumul += dy ; if (cumul >= dx) { cumul -= dx ; y += 1 ; } allume_pixel(x,y) ; } } |
||
| Décrire et implanter la technique que vous utiliseriez pour modifier cet algorithme pour qu’il réalise le dessin en 4-connexité (chaque pixel possède seulement 4 voisins : en haut, en bas, à droite, à gauche) par ajout des pixels supplémentaires nécessaires. | |||
On s ‘attachera à choisir ces pixels pour qu’ils soient les plus proches du segment continu. Ci-contre, le segment originel est dessiné en haut, tandis que le segment avec pixels supplémentaires est dessiné en bas |
|
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr