Correction
examen
de TD n°1 2007-2008
![]()
Correction
examen |
|
| 26 octobre 2007 - 1h30 | |
|
|
Question 1: VRML
a) Le champ position définit la position de la caméra. Le champ orientation définit la rotation (direction de l'axe puis angle) appliquée sur l'axe (0.0, 0.0, -1.0) pour obtenir la direction de visualisation de la caméra. Le champ focalDistance définit la distance sur l'axe de visualisation entre la caméra et un point visualisé nettement directement visé par la caméra. Le champ heightAngle définit l'angle d'ouverture verticale (en radian) mappé sur la hauteur de la fenêtre du viewer utilisé.
b) Le champ position est configuré avec les valeurs 100.0 0.0 100.0.
Le champ orientation définit la rotation qui, appliquée à l'axe de référence (0.0,
0.0, -1.0), le transforme en l'axe (-0.707, 0.0, -0.707) orienté de la position (100.0,
0.0, 100.0) vers la position (0.0, 0.0, 0.0). La rotation étant effectuée dans le plan
xz, elle est réalisée autour de l'axe (0.0, 1.0, 0.0). L'angle de rotation est de p/4 radians (45 degrés). L'angle de rotation est à valeur positive
car elle envoie l'axe -z vers l'axe -x.
Le champ focalDistance est configuré à la valeur de distance entre (100.0, 0.0, 100.0)
et (0.0, 0.0, 0.0) qui est égal à environ 141.4 (100*sqrt(2.0)).
c) On souhaite visualiser en gros plan un objet de taille 10.0 (2*5.0) situé à une distance de 141.4 dans le cadre d'une visualisation en perspective. Une estimation de l'angle d'ouverture verticale est donc atan(10.0/141.4) = atan(0,0707). Pour les petites valeurs d'angle données en radians, on peut considéré que atan(angle) = angle. -> Une valeur de 0.07 est utilisée.
#VRML V1.0 ascii
Separator {
PerspectiveCamera {
position 100 0 100
orientation 0 1 0 0.7854
focalDistance 141.4
heightAngle 0.07 }
Sphere {
radius 5 }
}
Question 2: Mathématiques pour l’Infographie
a) La modélisation par "coordonnées homogènes" est une technique
mathématique permettant de représenter des positions et des directions ainsi que
d'appliquer des transformations géométriques à ces positions et ces directions. En
coordonnées homogènes, les positions 3D sont représentées par les trois coordonnées
usuelles x, y et z ainsi qu'une 4ème coordonnée égale à 1.0 formant ainsi un vecteur
colonne de 4 composantes réelles. Les directions 3D sont représentées par les trois
coordonnées usuelles x, y et z ainsi qu'une 4ème coordonnée égale à 0.0 formant ainsi
un vecteur colonne de 4 composantes réelles. Les transformations géométriques sont
supportées par des matrices de 4x4 valeurs numériques réelles. La transformation d'une
position ou une direction par une transformation géométrique consiste à calculer le
produit matrice.vecteur de la matrice 4x4 support de la transformation et du vecteur 4x1
support de la position ou de la direction. Le résultat obtenu est une position pour une
position ou une direction pour une direction.
Des matrices existent pour toutes les transformations géométriques canoniques
(identité, translation, rotation, scale, ...). La composition de ces matrices canoniques
par produit matrice.matrice permet de concevoir des transformations élaborées.
b) Outre le fait d'autoriser la réalisation de transformations géométriques, l'utilisation des coordonnées homogènes possède les avantages suivants:
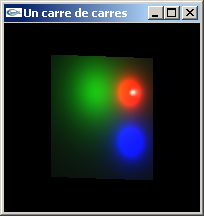
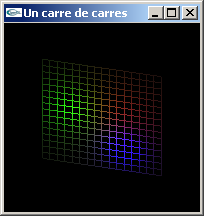
Question 3: Modélisation par facettes en OpenGL
La fonction développée prend l'entier n et le réel c en paramètres. La normale affectée aux sommets créés est toujours la même: (0.0, 0.0, 1.0). Les sommets sont créés au moyen de la fonction glVertex2f. La coordonnée z des sommets est alors implicitement fixée à 0.0. Les n*n facettes modélisant le carré peuvent être créées au moyen de deux techniques alternatives:
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Novembre 2007 */
/* Un carre de carres */
#include <GL/glut.h>
#include <GL/gl.h>
#include <GL/glu.h>
/* Dessin d'un carre au moyen d'une primitive */
/* de type GL_QUADS (n x n quads) */
void solution1(int n,float c) {
float ct = c / n;
c *= 0.5F;
glBegin(GL_QUADS);
glNormal3f(0.0F,0.0F,1.0F);
for ( int i = 0 ; i < n ; i++ )
for ( int j = 0 ; j < n ; j++ ) {
float xi = c-i*ct;
float yi = c-j*ct;
glVertex2f(xi,yi);
glVertex2f(xi-ct,yi);
glVertex2f(xi-ct,yi-ct);
glVertex2f(xi,yi-ct); }
glEnd();
}
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Novembre 2007 */
/* Un carre de carres */
#include <GL/glut.h>
#include <GL/gl.h>
#include <GL/glu.h>
/* Dessin d'un carre au moyen de plusieurs */
/* primitives de type GL_QUAD_STRIP */
/* (n quad_strips) */
void solution2(int n,float c) {
float ct = c / n;
c *= 0.5F;
glNormal3f(0.0F,0.0F,1.0F);
float yi;
float yf = -c;
for ( int j = 0 ; j < n ; j++ ) {
yi = yf;
yf += ct;
glBegin(GL_QUAD_STRIP);
float x = c;
for ( int i = 0 ; i <= n ; i++ ) {
glVertex2f(x,yi);
glVertex2f(x,yf);
x -= ct; }
glEnd(); }
}
Fichiers sources:

Question 4: OpenGL
a) L'exécution de la fonction void glLoadIdentity(void) entraine l'écrasement de la transformation géométrique courante (MODELVIEW ou PROJECTION) par la transformation identité.
b) L'exécution de la fonction void glRotatef(GLfloat angle, GLfloat dx, GLfloat dy,
GLfloat dz) entraine la composition de la transformation géométrique courante (MODELVIEW
ou PROJECTION) par une rotation.
Le suffixe f du nom de la fonction indique que le type des paramètres d'entête est le
type GLfloat. Le premier paramètre définit l'angle de rotation (en degrés). Les
paramètres deux, trois et quatre définissent la direction de l'axe de rotation. Celui-ci
passe implicitement par l'origine. (dx, dy, dz) n'est pas obligatoirement une direction
normée mais ne peut pas être la direction nulle.
c) L'exécution de la fonction void gluPerspective(GLdouble ouverture, GLdouble ration,
GLdouble dmin, GLdouble dmax) entraine la composition de la transformation géométrique
courante (généralement PROJECTION) par la transformation de mise en perspective. Il
s'agit d'une fonction de la bibliothèque glu. La caméra virtuelle de visualisation est
placée à l'origine. Elle est orientée selon l'axe -z. Les paramètres d'entête
définissent les caractéristiques géométriques du volume de visualisation. Le premier
paramètre définit l'angle d'ouverture verticale (en degrés) ajusté à la hauteur du
viewport de visualisation. Le deuxième paramètre est le facteur qui multiplié par le
premier paramètre donne l'angle d'ouverture horizontale (en degrés) ajusté à la
largeur du viewport de visualisation. Les troisième et quatrième paramètres
définissent l'intervale en z en dehors duquel les objets ou morceaux d'objets ne sont pas
visualisés.
-> Un objet n'est visualisé que si sa coordonnée z est comprise entre -dmax et -dmin.
Question 5: Animation avec OpenGL et GLUT
a) Une variable globale réelle initialisée à 0.0 stocke l'angle de rotation instantané de l'animation. La fonction idle incrémente cet angle de 1° et poste un événement redisplay via l'exécution de la fonction glutPostRedisplay(). L'angle est utilisé dans la fonction display.
b) Une variable globale réelle supplémentaire stocke la distance entre le centre des 2 objets et le centre de rotation. Cette variable est initialisée à 2.0. Outre la gestion de l'angle de rotation, la fonction idle décrémente la distance au centre de -0.0005, seuille cette distance à 1.0F pour que les deux objets ne penètrent pas l'un dans l'autre mais tangentent seulement et enfin poste un événement redisplay via glutPostRedisplay(). L'angle et la distance sont utilisés dans la fonction display.
Une sphère et un cube en rotation
|
Quelques indications sur l'évaluation Chaque exercice a été noté sur 10. La note globale est approximativement égale à la somme des notes sur 10 divisée par 2. Il était donc attendu la réalisation complète de 4 exercices sur 5 pour l'obtention de la note maximale. |
|
|
Remarques, erreurs |