Examen de TD n°2 2007-2008
![]()
![]()
Le cas échéant, on n'oubliera pas de fournir quelques commentaires sur les techniques employées.
Question 1: Lancer de rayons
On considère une sphère S de rayon r centrée sur la position (cx, cy, cz). On considère la position d'un point d'incidence P de coordonnées (x, y, z) sur cette sphère. Définir sans l'implanter une méthode de calcul de la normale extérieure à la sphère S au point P.
Question 2: Courbes paramétriques cubiques et surfaces paramétriques bicubiques
On considère la fonction de prototype suivant : position *calculBSpline(position *pts, matriceDeBase m, int n); développée en TD/TP pour calculer la position de n points uniformément répartis (dans l'intervalle [0.0, 1.0]) sur la courbe paramétrique cubique de matrice de base m et de points de contrôle pts (pts est un tableau de 4 position).
typedef struct position {
double x;
double y;
double z;
double t; } position;
typedef double matriceDeBase[4][4];
On va utiliser cette fonction pour générer n*n sommets de définition d'une " surface paramétrique bicubique " à partir d'un maillage de 4 jeux de 4 points de contrôle (4 quadruplets) soit au total 16 points de contrôle. Chacun des quadruplets est utilisé pour générer une courbe cubique définie sur n sommets. Les 4 jeux de n sommets ainsi obtenus sont utilisés pour définir n jeux de 4 points de contrôle (lignes continues courbes sur le schéma ci-dessous) de manière à autoriser la génération de n courbes cubiques de n sommets (lignes courbes en pointillé sur le schéma ci-dessous). On obtient ainsi n*n sommets définissant une surface paramétrique bicubique.
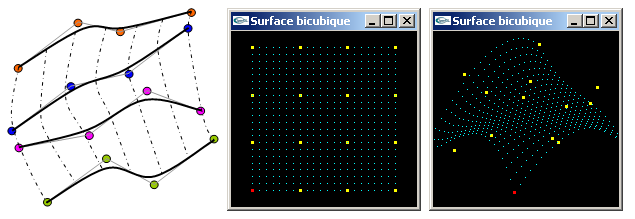
Ecrire une fonction respectant le prototype position **calculSurfaceBSpline(position **pts, matriceDeBase m, int n); calculant les n*n sommets d’une surface paramétrique bicubique selon la méthode définie ci-dessus (pts est un tableau de 4x4 position).
Question 3: Caméra en OpenGL
Ecrire la fonction reshape d'un programme C + OpenGL + GLUT qui configure une caméra de visualisation en perspective selon les caractéristiques suivantes:
- Elle est placée en position (100.0, 50.0, 50.0).
- Elle est dirigée vers le point de coordonnées (-100.0, -50.0, -200.0).
- La direction de la verticale est la direction x.
- Le ratio d'ouverture de la caméra est ajusté au ratio de la fenêtre de visualisation.
- L'ouverture horizontale est de 30.0 degrés.
- Les plans de clipping near et far sont respectivement aux distances (en -z) 235.0 et 435.0 de la caméra.
Question 4: Lumières en OpenGL
Ecrire une fonction C + OpenGL permettant d'activer et de paramétrer les trois premières lumières définissable en OpenGL selon les caractéristiques suivantes:
- Première lumière
- Type lumière ponctuelle
- Position : (10.0, 5.0, 10.0)
- Couleur en lumière diffuse : rouge
- Couleur en lumière spéculaire : vert
- Couleur en lumière ambiante : noir
- Deuxième lumière
- Type lumière directionnelle
- Direction du vecteur éclairage : (1.0, 0.0, -1.0)
- Couleur en lumière diffuse : bleu
- Couleur en lumière spéculaire : jaune
- Couleur en lumière ambiante : noir
- Troisième lumière
- Type spot
- Position : (10.0, 2.0, 10.0)
- Direction du cône d'éclairage : (-1.0, 0.0, -1.0)
- Ouverture du cône d'éclairage : 20.0°
- Pas d'atténuation centre vers bord
- Couleur en lumière diffuse : cyan
- Couleur en lumière spéculaire : magenta
- Couleur en lumière ambiante : gris à 25%
Question 5: Mathématiques matricielles
On considère la suite de transformations géométriques consistant chronologiquement en
- une rotation R1 d'angle ax autour de l'axe Ox
- une translation T1 de vecteur (dx1, dy1, dz1)
- une translation T2 de vecteur (dx2, dy2, dz2)
- une rotation R2 d'angle ay autour de l'axe Oy
Calculer la matrice de transformation en coordonnées homogènes représentative de cette suite de 4 transformations.
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr