Correction examen
de TD n°2 2012-2013
21 décembre 2012 - 1h35
![]()
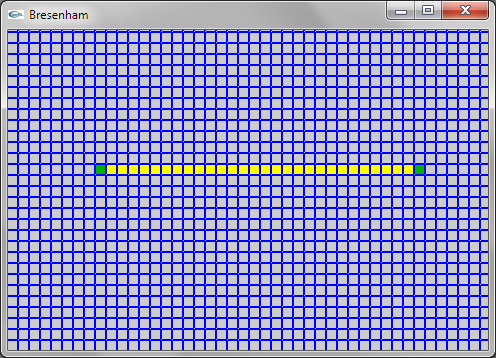
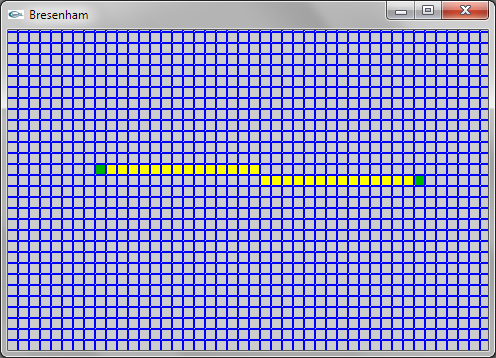
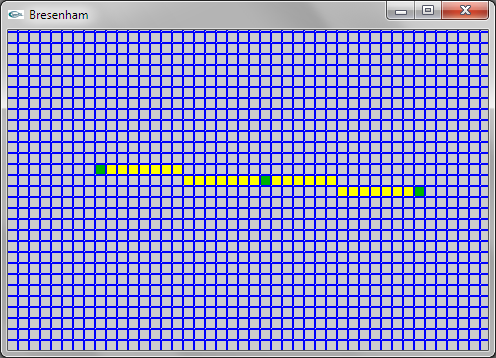
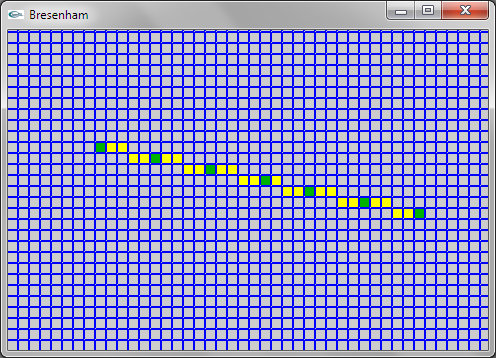
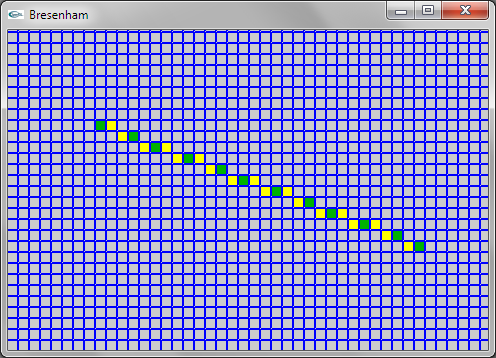
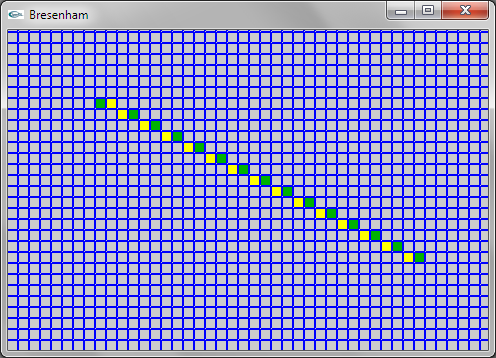
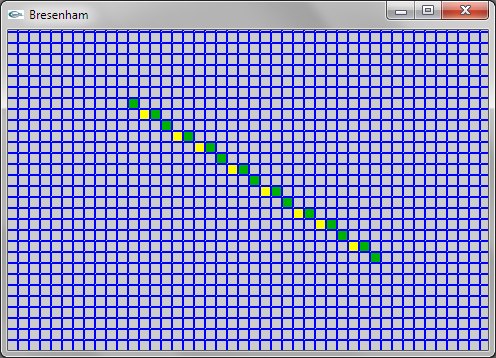
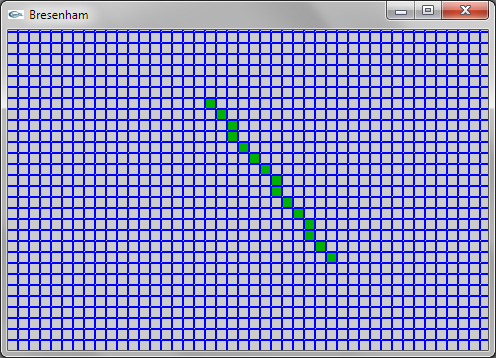
Question 1: Bresenham
Une solution consiste à modifier la partie de l'algorithme itérant en x (pour déterminer l'ordonnée correspondant à chaque abscisse) de manière à déterminer les abscisses minimale et maximale sur chaque trame horizontale d'ordonnée y et allumer le pixel à distance intermédiaire entre x minimum et x maximum pour chaque y.
Une solution plus efficace consiste à ne conserver que la partie itérant en y (car il y a un pixel à allumer pour chaque y). On se trouve alors confronté au problème que plusieurs déplacements de 1 (ou -1 suivant xinc) en x doivent éventuellement être réalisés à chaque y. Ce problème est résolu en transformant le if en un while.
Dans les deux solutions, le traitement des premier et dernier pixels allumés est à gérer de manière spécifique pour que le premier pixel soit celui de coordonnées (xi,yi) et le dernier soit celui de coordonnées (xf,yf) et pour que deux pixels soient allumés dans le cas où yi = yf.
Les deux solutions sont présentées ci-dessous.
Programme complet: Bresenham.cpp
void ligne1(int xi,int yi,int xf,int yf) {
int dx,dy,i,xinc,yinc,cumul,x,y,x1;
x = xi;
y = yi;
dx = xf - xi;
dy = yf - yi;
xinc = ( dx > 0 ) ? 1 : -1;
yinc = ( dy > 0 ) ? 1 : -1;
dx = abs(dx);
dy = abs(dy);
allumePixel(xi,yi);
if ( dx > dy ) {
cumul = dx / 2;
for ( i = 1 ; i <= dx ; i++ ) {
x += xinc;
cumul += dy;
if ( cumul >= dx ) {
if ( ( y != yi ) && ( y != yf ) ) {
allumePixel((x1+x-xinc)/2,y); }
cumul -= dx;
y += yinc;
x1 = x; } }
allumePixel(xf,yf); }
else {
cumul = dy / 2;
for ( i = 1 ; i <= dy ; i++ ) {
y += yinc;
cumul += dx;
if ( cumul >= dy ) {
cumul -= dy;
x += xinc; }
allumePixel(x,y); } }
}
void ligne2(int xi,int yi,int xf,int yf) {
int dx,dy,i,xinc,yinc,cumul,x,y;
x = xi;
y = yi;
dx = xf - xi;
dy = yf - yi;
xinc = ( dx > 0 ) ? 1 : -1;
yinc = ( dy > 0 ) ? 1 : -1;
dx = abs(dx);
dy = abs(dy);
allumePixel(x,y);
cumul = dy / 2;
for ( i = 1 ; i <= dy ; i++ ) {
y += yinc;
cumul += dx;
while ( cumul >= dy ) {
cumul -= dy;
x += xinc; }
allumePixel(x,y); }
if ( yi == yf )
allumePixel(xf,yf);
}
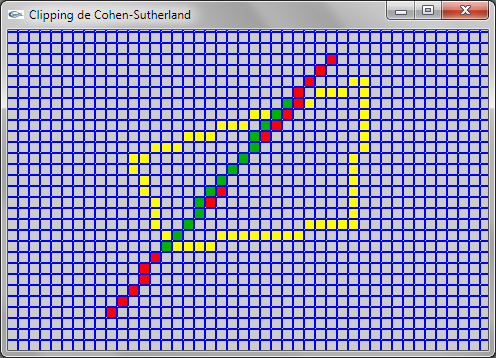
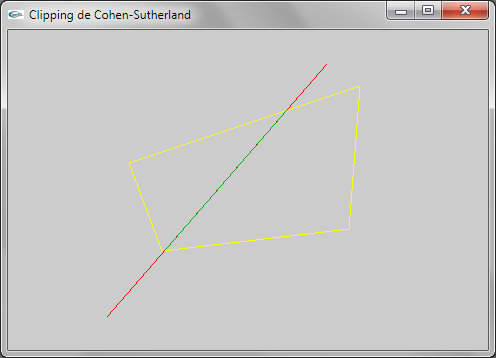
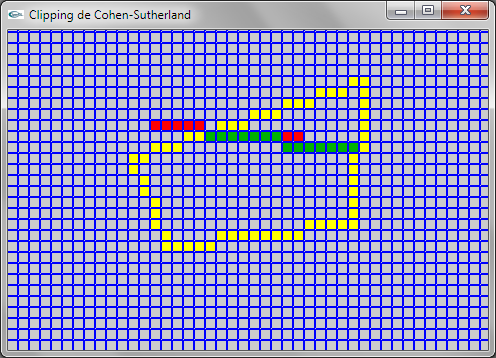
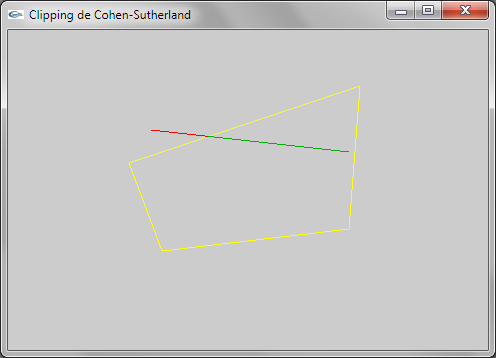
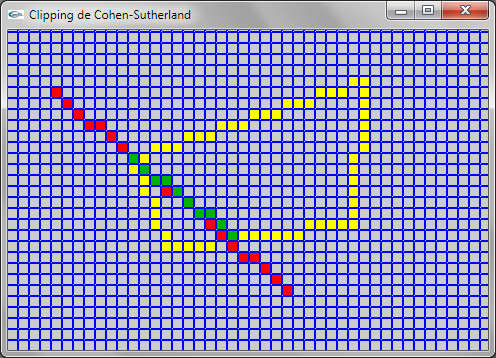
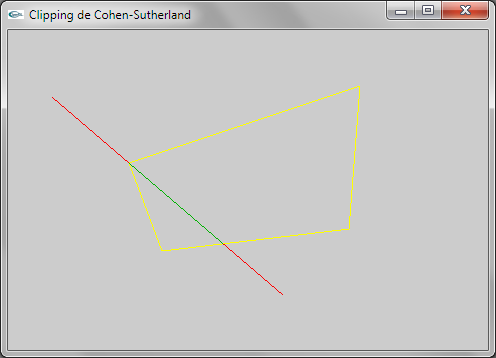
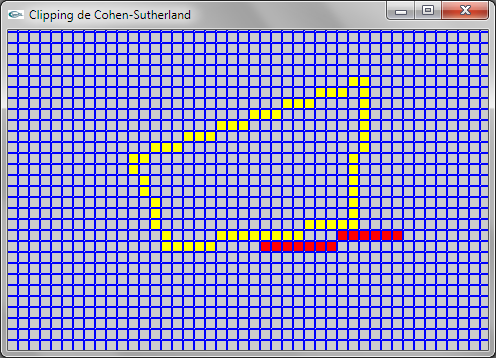
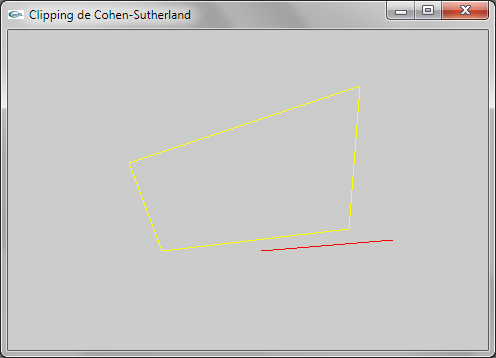
Question 2: Cohen-Sutherland
L'adaptation est assez simple. En réalité, le cas du clipping dans un rectangle à cotés parallèles aux axes
est un cas simplifié du cas général consistant à clipper un segment dans un quadrilatère. La simplification porte
sur la détermination de la position d'une extrémité vis à vis des droites sous-tendues par les cotés (un simple
test de comparaison) ainsi que sur les calculs de déplacement des extrémités du segment (la formule de calcul
de la nouvelle position est plus simple car on connait l'une des coordonnées et on en déduit l'autre).
En résumé:
- Le code de Cohen-Sutherland d'une extrémité est établi sur 4 valeurs booléennes car un quadrilatère
a 4 cotés.
- Tester la position d'une extrémité vis à vis d'un coté nécessite de calculer l'équation cartésienne
a*x+b*y+c=0.0 de la droite sous-tendant le coté. Si pour un point de position (px,py), la valeur a*px+b*py+c est
supérieure à zéro, alors on est "dedans", sinon on est "dehors". Les valeurs a,b et c sont
calculées au moyen des coordonnées des 2 sommets définissant le coté.
- Déplacer une extrémité revient à la reporter sur l'intersection entre la droite sous-tendant le segment
et la droite sous-tendant le coté vers lequel le déplacement est réalisé. Il est donc ici nécessaire d'implanter
le calcul de l'intersection de 2 droites (système de 2 équations linéaires à deux inconnues).
- La réalisation de calculs sur des réels impose de gérer un facteur de précision EPSILON pour les tests
après opérations mathématiques.
- L'existence de divisions dans les calculs réalisés imposent de se prémunir à l'encontre d'éventuelles
divisions par 0.0. Soit elles sont algorithmiquement possibles, il faut alors gérer des traitements exceptionnels.
Soit elles sont algorithmiquement impossibles.
Une remarque très importante est que l'adaptation ne fonctionne que dans le cas où les quadrilatères sont convexes car dans le cas contraire, le codage des extrémités par 4 booléens ne fonctionne pas.
L'implantation, non demandée lors de l'épreuve, est fournie ci-dessous.
Programme complet: Cohen-Sutherland-Quadrilatere.cpp, Quadrilatere2D.h, Quadrilatere2D.cpp, Segment2D.h, Segment2D.cpp, TraceSegment.h, TraceSegment.cpp et classes utilitaires
/* Affectation a une Position2D de la position */
/* de l'intersection entre un Segment2D */
/* et un cote du quadrilatere */
void Quadrilatere2D::affecteIntersection(Position2D *p,
Segment2D *s,
int cote) {
double as = s->p1->c[1]-s->p2->c[1];
double bs = -(s->p1->c[0]-s->p2->c[0]);
double cs = -(as*s->p1->c[0]+bs*s->p1->c[1]);
double y = -(-a[cote]*cs+c[cote]*as)/(-a[cote]*bs+b[cote]*as);
p->c[0] = ( as ) ? -(cs+bs*y)/as : -(c[cote]+b[cote]*y)/a[cote];
p->c[1] = y;
}
/* Determination de la position d'un point */
/* vis a vis d'un des 4 cotes */
/* du quadrilatere */
int Quadrilatere2D::position(Position2D *p,int cote) {
return( p->c[0]*a[cote]+p->c[1]*b[cote]+c[cote] > 0.0001 );
}
/* Code de Cohen-Sutherland d'une Position2D */
int Quadrilatere2D::code(Position2D *p) {
int cd = 0;
if ( position(p,0) )
cd += 1;
if ( position(p,1) )
cd += 2;
if ( position(p,2) )
cd += 4;
if ( position(p,3) )
cd += 8;
return(cd);
}
/* Clipping de Cohen-Sutherland vis a vis */
/* d'un quadrilatere suppose convexe */
int Quadrilatere2D::clip(Segment2D *s) {
update();
int c1 = code(s->p1);
int c2 = code(s->p2);
while ( ( ( c1 != 0 ) || ( c2 != 0 ) ) &&
( (c1&c2) == 0 ) ) {
if ( c1 == 0 ) {
{ Position2D *aux = s->p1;
s->p1 = s->p2;
s->p2 = aux; }
{ int aux = c1;
c1 = c2;
c2 = aux; } }
if ( (c1&1) != 0 ) {
affecteIntersection(s->p1,s,0); }
else
if ( (c1&2) != 0 ) {
affecteIntersection(s->p1,s,1); }
else
if ( (c1&4) != 0 ) {
affecteIntersection(s->p1,s,2); }
else {
affecteIntersection(s->p1,s,3); }
c1 = code(s->p1); }
return(( c1 == 0 ) && ( c2 == 0 ));
return(1);
}
Question 3: Mathématiques
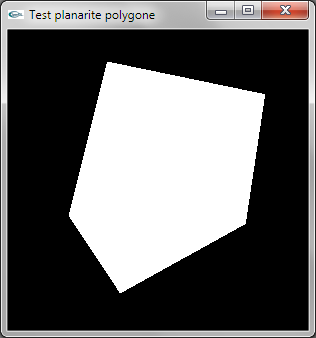
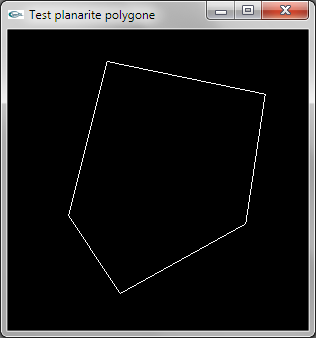
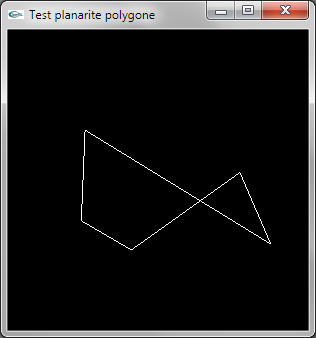
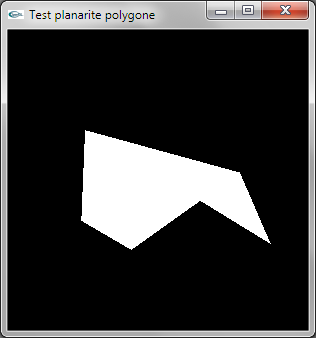
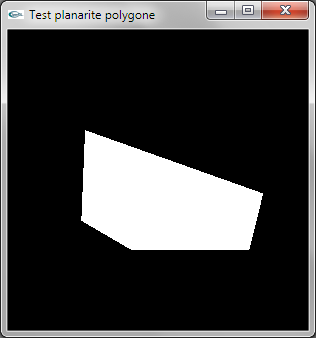
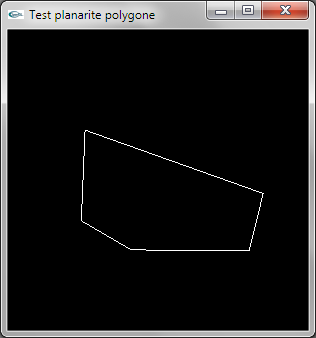
On extrait le vecteur orthogonal N au premier triplet de sommets du polygone formant un triangle T non dégénéré
(une vraie surface). S est l'un au choix des sommets de T. L'extraction de N est réalisée en calculant
le produit vectoriel entre les deux directions formées par 2 cotés de T. Le but est d'obtenir ici une direction
N différente du vecteur nul (cas où la facette est dégénérée).
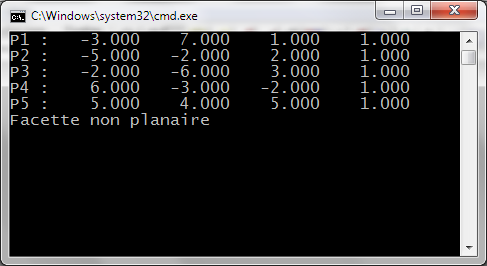
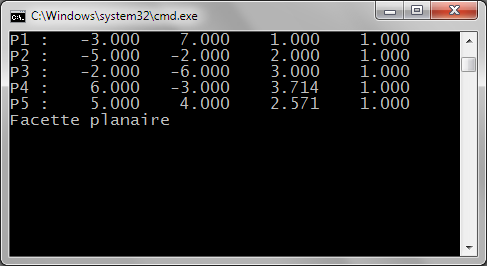
On vérifie ensuite si l'ensemble des n-3 autres sommets Si du polygone est dans le plan de T. Pour cela, la
direction formée par S et Si doit être orthogonale à N. Pour tester l'orthogonalité, on utilise le produit
scalaire. Celui-ci est égal à 0.0 en cas d'orthogonalité. Dès le premier produit scalaire non nul trouvé,
on peut conclure à la non planarité.
L'implantation, non demandée lors de l'épreuve, est fournie ci-dessous.
Programme complet: PlanaritePolygone.cpp, Polygone3D.h, Polygone3D.cpp, Classes utilitaires
/* Test de planarite */
const double EPSILON = 0.000001;
static int vecteurNul(Direction3D *d) {
return( (abs(d->c[0]) < EPSILON ) &&
(abs(d->c[1]) < EPSILON ) &&
(abs(d->c[2]) < EPSILON ) );
}
int Polygone3D::testPlanarite(void) {
Direction3D *d12;
int p = 0;
do {
d12 = new Direction3D(t[p],t[(p+1)%n]);
Direction3D *d13 = new Direction3D(t[p],t[(p+2)%n]);
d12->produitVectoriel(d13);
delete(d13); }
while ( vecteurNul(d12) );
for ( int i = 3 ; i < n ; i++ ) {
Direction3D *d = new Direction3D(t[p],t[(p+i)%n]);
double ps = d->produitScalaire(d12);
delete(d);
if ( abs(ps) > EPSILON ) {
delete(d12);
return(0); } }
delete(d12);
return(1);
}
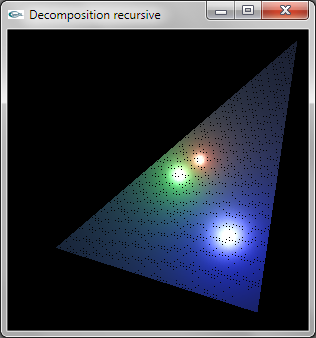
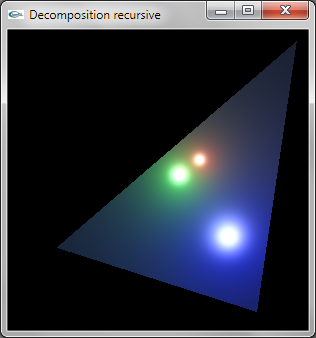
Question 4: Modélisation OpenGL
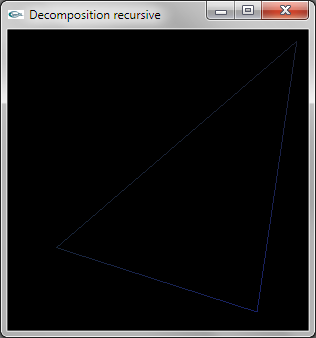
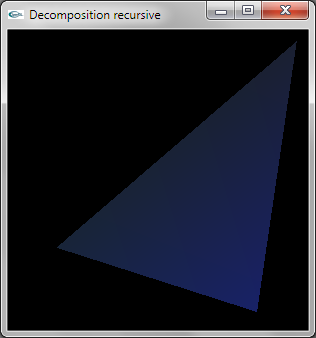
La décomposition est réalisée de manière récursive.
Au niveau de récursivité 0, la facette ne doit pas être décomposée et est modélisée par une primitive OpenGL de
type GL_TRIANGLE.
Au niveau de récursivité n différent de 0, la facette doit être décomposée et n'est pas modélisée en OpenGL.
Les trois sommets permettent de calculer les trois sommets intermédiaires situés au milieu des 3 cotés. La relance
récursive est réalisée par 4 appels au niveau n-1 sur les 4 triplets de sommets formant les 4 triangles de décomposition.
Il convient de prendre garde à l'ordre des sommets pour ne pas les fournir dans un autre sens que celui de
la facette originelle.
La normale à la facette originelle est calculée pour être spécifiée comme normale à toutes les facettes.
Programme complet: DecompositionFacette.cpp, Classes utilitaires
/* Scene dessinee */
static void position3DIntermediaire(Position3D *si,
Position3D *sf,
Position3D *p) {
p->c[0] = (si->c[0]+sf->c[0])/2.0;
p->c[1] = (si->c[1]+sf->c[1])/2.0;
p->c[2] = (si->c[2]+sf->c[2])/2.0;
}
static void decompositionRecursiveFacette(int n,
Position3D *s1,
Position3D *s2,
Position3D *s3) {
if ( n ) {
Position3D s12;
Position3D s23;
Position3D s31;
position3DIntermediaire(s1,s2,&s12);
position3DIntermediaire(s2,s3,&s23);
position3DIntermediaire(s3,s1,&s31);
decompositionRecursiveFacette(n-1,s1,&s12,&s31);
decompositionRecursiveFacette(n-1,s2,&s23,&s12);
decompositionRecursiveFacette(n-1,s3,&s31,&s23);
decompositionRecursiveFacette(n-1,&s31,&s12,&s23); }
else {
glVertex3f(s1->c[0],s1->c[1],s1->c[2]);
glVertex3f(s2->c[0],s2->c[1],s2->c[2]);
glVertex3f(s3->c[0],s3->c[1],s3->c[2]); }
}
static void affichageFacette(int n,
Position3D *s1,
Position3D *s2,
Position3D *s3) {
glPushMatrix();
Direction3D *nm = new Direction3D(s1,s2);
Direction3D *d = new Direction3D(s1,s3);
nm->produitVectoriel(d);
nm->normalisation();
glNormal3f(nm->c[0],nm->c[1],nm->c[2]);
delete(d);
delete(nm);
glBegin(GL_TRIANGLES);
decompositionRecursiveFacette(niveau,s1,s2,s3);
glEnd();
glPopMatrix();
}
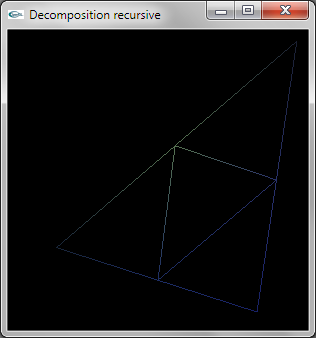
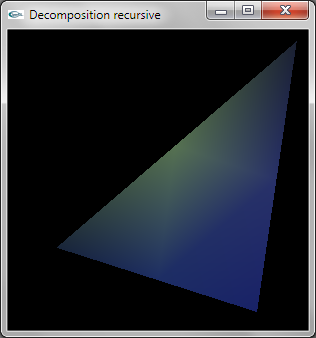
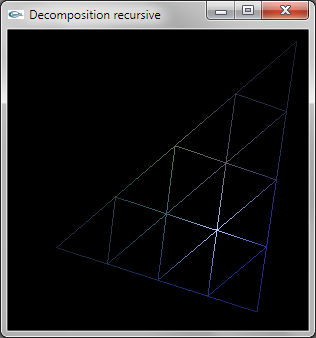
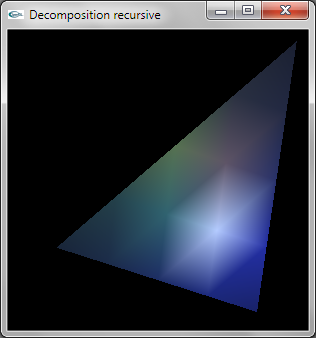
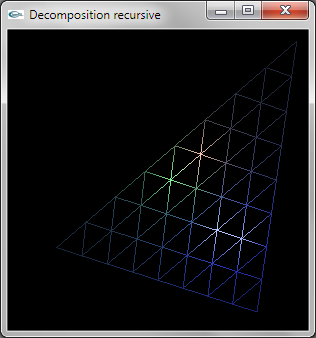
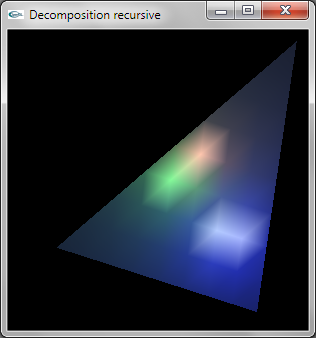
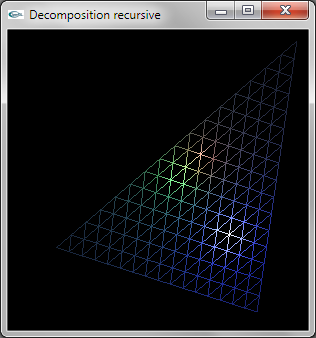
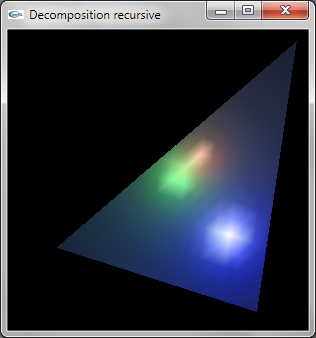
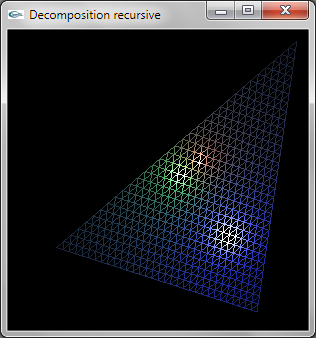
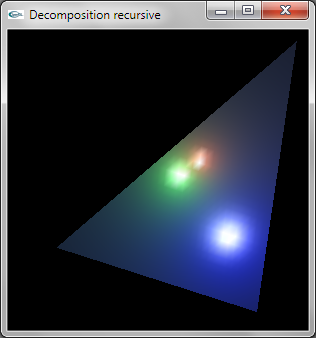
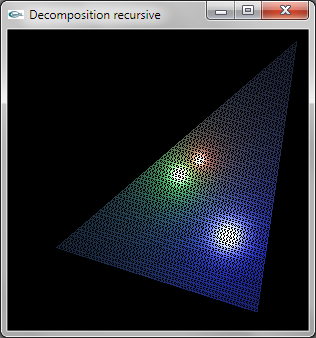
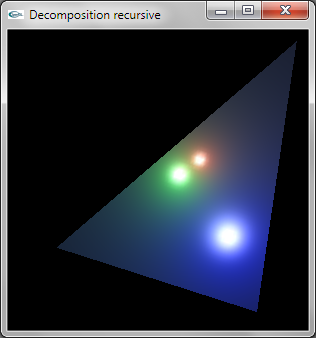
L'implantation récursive est peu efficace car elle entraine le calcul de 3*n4 sommets. On pourrait implanter une décomposition plus efficace en traçant n+1 TRIANGLE_STRIP.