Première session 2001-2002
Etablir la matrice de transformation définissant une symétrie par rapport au
plan orthogonal au vecteur ![]() et passant par le point
O. La matrice de transformation
et passant par le point
O. La matrice de transformation 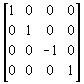 réalise la
symétrie par rapport au plan xOy.
réalise la
symétrie par rapport au plan xOy.
On exprimera cette transformation sous la forme d'un produit de transformations géométriques canoniques sans calculer explicitement la matrice produit.
Question 2: OpenGL + GLUt
On souhaite visualiser une scène en perspective selon les caractéristiques suivantes:
- Le point visé est l'origine.
- La caméra de visualisation est placée en position (0.0, 30.0, 50.0).
- L'axe vertical de la caméra est l'axe (0.0,1.0,0.0) du repère global.
- La caméra de visualisation possède une ouverture verticale de 15°.
- La visualisation conserve les proportions en x et en y.
- L'objet le plus proche de la caméra est à une distance de 30.0. Celui le plus loin est à une distance de 100.0.
Ecrire une fonction reshape OpenGL vérifiant au mieux ces caractéristiques.
Question 3: Algorithmique de l'Infographie
On utilise l'algorithme de Bresenham pour tracer des segments de droite sur un écran bitmap. Lors des tracés consécutifs de deux segments, il est possible que des pixels allumés avec une certaine couleur pour le premier, soient recouverts lors du tracé du second.
Ecrire une fonction permettant de tester cette éventualité. Cette fonction ne devra pas effectuer d'opération de traçage effective sur l'écran bitmap, mais seulement un test.
Question 4: Modélisation en OpenGL
Ecrire une fonction display OpenGL permettant de réaliser l'affichage d'une pyramide à base triangulaire constituées de sphères blanches de rayon 1 sous un éclairage directionnel blanc orienté selon l’axe -z. Cette pyramide sera formée d’un nombre arbitraire n de couches superposées de sphères empilées les unes sur les autres. La couche du haut comporte une sphère. Celle en dessous, en comporte 3. Celle encore en dessous en possède 6, et ainsi de suite: 10, 15, 21, 28,... pour les couches suivantes. L'agencement est réalisée pour que les sphères soient accolées les unes aux autres.
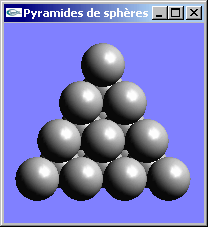
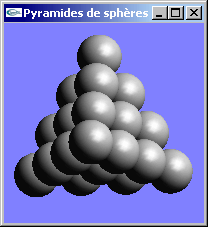
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr