Seconde session 2002-2003
On considère une courbe B-Spline de Catmull-Rom définie sur 4 sommets d'un espace à trois dimensions. Déterminer la formule de calcul de la tangente en chaque point de la courbe.
Question 2
| On souhaite programmer en OpenGL une chenille schématisée. Elle est constituée de n sphères de rayon r régulièrement réparties selon le schéma ci-contre. | 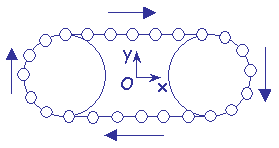 |
Le rayon des cercles est rc. La distance entre leurs centres est dc.
a) Ecrire la fonction display d'un programme OpenGL + GLUT dessinant cette scène
b) Ecrire les fonctions idle et display d'un programme OpenGL + GLUT dessinant cette
scène avec une animation consistant à déplacer les sphères d'une distance d entre
chaque image.
-> La chenille tourne sur place.
Question 3
On considère une scène stockée dans un fichier VRML portant le nom scene.wrl. Elle occupe un volume équivalent à un cube de coté 15 centré sur l'origine.
Ecrire un fichier VRML dessinant cette scène placée en position (10.0, 10.0, 10.0). Elle devra être éclairée par trois sources lumineuses répondant aux caractéristiques suivantes:
(1) lumière ponctuelle placée en position (30.0, 40.0, 50.0) éclairant dans le jaune,
(2) lumière directionnelle de direction (0.0, 1.0, -1.0) éclairant dans le magenta,
(3) spot placé en position (-30.0,10.0,50.0) éclairant dans le cyan le centre de la scène avec une ouverture de 10°.
La scène sera munie d'un matériau diffusant dans le blanc et réfléchissant spéculairement dans le rouge.
Question 4
On considère un polygone de R2 définissant n sommets à abscisses positives. On se sert de ce polygone comme d'un profil de révolution autour de l'axe Oy de R3 de manière à définir un volume de révolution.
a) Définir une structure de données Polygone.
b) Ecrire une fonction OpenGL modélisant par facettes le volume de révolution associé à un polygone. La fonction devra assurer la génération des facettes, des normales nécessaires au calcul d'illumination et des coordonnées de texturage.
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr