Correction
examen de TD 2001-2002
RETOUR
Exercice 1: OpenGL
Question a)
La fonction init ne doit réaliser que les instructions devant être exécutées une seule fois au début du programme. Définition du matériel d'affichage, des paramètres constants des deux lumières, des paramètres d'OpenGL,...
Question b)
La fonction display doit réaliser le dessin d'une seule image de l'animation. La lumière est animée par modification, de son axe d'éclairage via un glRotatef encadré dans un glPushMatrix - glPopMatrix de manière que cette rotation ne porte pas aussi sur la scène. L'angle utilisé dans le glRotatef est modifié au sein de la fonction idle. Les sphères ,ayant pour rayon 1, devront être écartées de 2 pour être accolées.
Question c)
La fonction idle doit réaliser la modification de la variable globale utilisée dans la fonction display. Elle ne doit contenir aucun appel de fonction OpenGL de manière à contrôler plus facilement le flux de ces instructions au cours de l'exécution événementielle du programme avec interface GLUt. La fonction idle devra se terminer par un appel à glutPostWindowRedisplay() pour mettre en fil d'attente un événement de réaffichage de la fenêtre de dessin et donc réaliser l'exécution de l'animation.
Avec une ouverture de 50° au lieu de 15°
Une méthode simple pour tester le
parallélisme de deux facettes triangulaires consiste à vérifier si un vecteur
orthogonal à l'une d'elles est aussi orthogonal à deux des cotés de l'autre.
Pour obtenir un vecteur orthogonal à une facette F, on calculera le produit vectoriel
entre deux des cotés de F.
Pour vérifier l'orthogonalité entre deux vecteurs, on peut en calculer le produit
scalaire. Si celui-ci est égal à zéro, les deux vecteurs sont orthogonaux.
L'équation paramétrique d'une s
phère de centre 0, de rayon 1 dans l’espace (3D) est: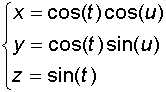
, t appartient à [-p/2,p/2] (parallèles), u appartient à [0,2p] (méridiens)
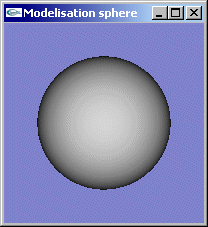
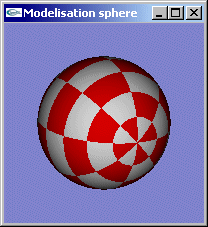
On construit (n+1)*(n+1) sommets en itérant pour i entre 0 et n pour t entre [-p/2,p/2], et j entre 0 et n pour u entre [0,2p] selon l'équation paramétrique. Chaque facette quadrangulaire ij sera définie en considérant les sommets (i,j), (i+1,j), (i+1,j+1) et (i,j+1) pour i entre 0 et n-1 et j entre 0 et n-1. On définit ainsi n*n facettes quadrangulaires pour la modélisation de la sphère. Les normales aux sommets sont égales aux positions des sommets car l'objet est régulier autour de l'origine et de rayon 1. Les coordonnées de texturage peuvent être calculées régulièrement entre 0.0 et 1.0 pour chacun des sommets de la sphère en fonction des indices (i,j) du sommet entre 0 et n.
Remarques, erreurs
nicolas.janey@univ-fcomte.fr