Correction
examen de TD 2002-2003
![]()
Exercice 1: VRML
Cet exercice est destiné à faire manipuler les fichiers VRML, le noeud
WWWInline et surtout le noeud PerspectiveCamera.
On rappelle:
- que les caméras VRML ont par défaut un axe de visualisation orienté selon la
direction -z (0.0, 0.0, -1.0) depuis la position donnée par le champ position
- que le champ orientation permet de réaliser une rotation de cet axe par la donnée d'un
axe de rotation et d'un angle de rotation (en radian),
- que le champ heightAngle définit l'angle d'ouverture verticale de la caméra (en
radian)
Question a)
Placée en position (0.0, 0.0, 100.0), la caméra regarde par défaut l'origine en (0.0, 0.0, 0.0). Le champ orientation n'a donc pas à être renseigné. L'ouverture verticale est de l'ordre de 10.0/(100.0-e) radians. Après essais, on trouve 0.14 radians.
| #VRML V1.0 ascii Separator { PerspectiveCamera { position 0 0 100 heightAngle 0.14 } WWWInline { name "Scene.wrl" bboxSize 10 10 10 } } |
|
Question b)
Placée en position (-100.0,0.0,100.0), la caméra doit être orientée selon l'axe (1.0,0.0,-1.0) pour viser l'origine. On évalue facilement qu'une rotation de -p/4 peut être réalisée autour de l'axe Oy pour assurer cette rotation. L'ouverture verticale est de l'ordre de 10.0/(140.0-e) radians. Après essais, on trouve 0.10 radians.
| #VRML V1.0 ascii Separator { PerspectiveCamera { position -100 0 100 heightAngle 0.10 orientation 0 1 0 -0.7854 } WWWInline { name "Scene.wrl" bboxSize 10 10 10 } } |
|
Question c)
Placée en position (-100.0,-100.0,100.0), la caméra doit être orientée
selon l'axe (1.0,1.0,-1.0) pour viser l'origine. La détermination d'une rotation de l'axe
(0.0,0.0,-1.0) pour l'obtenir n'est pas triviale.
Solution (1): Effectuer une rotation de p radians (180°)
autour de l'axe B bissecteur de nos deux axes. Pour déterminer cet axe, on norme chacun
des deux axes et on en fait la somme.
B = (0.0,0.0,-1.0) + (1.0,1.0,-1.0)/sqrt(3)
= (0.0,0.0,-1.0) + (0.577,0.577,-0.577)
= (0.577,0.577,-1.577)
Pour l'angle d'ouverture verticale, on reste sur des valeurs du même ordre car l'objet
s'est éloigné, mais est vu sous un point de vue différent qui le fait apparaître plus
gros.
| #VRML V1.0 ascii Separator { PerspectiveCamera { position -100 -100 100 heightAngle 0.1 orientation 0.577 0.577 -1.577 3.14159 } WWWInline { name "Scene.wrl" bboxSize 10 10 10 } } |
|
Solution (2): Trouver un axe orthogonal aux deux axes (produit vectoriel)
et effectuer une rotation de l'angle entre les deux axes (arcosinus du produit scalaire
après normalisation des deux axes).
B' = (1.0,-1.0,0.0)
q = acos(0.57735) = 0.955 radian
Cette deuxième solution fournit un affichage différent de la première (inversé).
La génération des sommets du tore est assurée algorithmiquement par
deux itérations imbriquées.
La première fera varier a entre 0 et 2p
([0,2p[) par pas de 2p/nbe.
La deuxième fera varier b entre 0 et 2p
([0,2p[) par pas de 2p/nbi.
On utilise l'équation donnée avec chaque couple de valeurs a
et b pour calculer chaque sommet.
nbe bandes (GL_QUAD_STRIP) de nbi facettes quadrangulaires sont générées de manière à
constituer le tore bande après bande. Il est aussi possible de construire le tore avec
nbi bandes de nbe facettes (les boucles sont imbriquées dans l'autre sens).
Pour déterminer les coordonnées des normales, le système d'équations définissant les
coordonnées des sommets du tore peut être dérivé une fois selon a
pour déterminer une tangente au tore, puis une seconde fois selon b
pour déterminer une seconde tangente. Il reste ensuite à faire le produit vectoriel des
deux tangentes obtenues pour déterminer la normale. Ce calcul est extrèmement fastidieux
à réaliser à la main. On se rend compte intuitivement que la normale au sommet
correspondant au couple (a,b) est
équivalente à celle générée pour ce sommet sur la sphère de rayon re et de centre
(ri cos(b), ri sin(b), 0.0). Ce qui
donne le système d'équations paramétriques suivant:
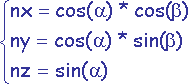
Pour générer les coordonnées de texturage, une possibilité consiste à les évaluer uniformément entre 0 et 1 (b/2p) sur le pourtour du tore pour la première coordonnée de texturage (s) et uniformément entre 0 et 1 (a/2p) sur le pourtour des sections de tore pour la seconde coordonnée (t).
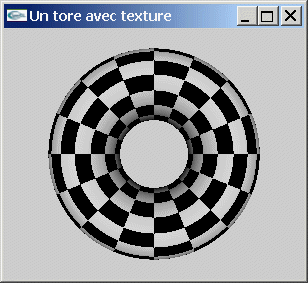
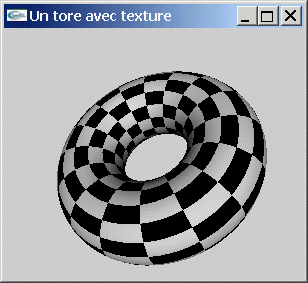
Fichier
source complet: TextureTore.cpp
Modules utilitaires: Modules.zip
La difficultée essentielle de l'exercice réside dans le fait que si les
sphères sont uniformément réparties sur le périmètre du carré, leur nombre sur
chaque coté du carré n'est pas uniforme car le nombre de sphères (3*n) n'est pas
forcément divisible par 4.
Les solutions algorithmiques sont multiples. On pourra par exemple construire une
itératio sur les sphères (entre 0 et 3*n-1) ou bien sur les cotés du carré (entre 0 et
3). Si on itère sur les sphères, on pourra choisir de travailler en référence absolue
en calculant la position de chaque sphère compte tenu de son numéro dans la suite de
sphères, ou bien encore en référence relative en définissant la position d'une sphère
à partir de la position de celle qui la précède immédiatement (par translation et
éventuellement rotation).
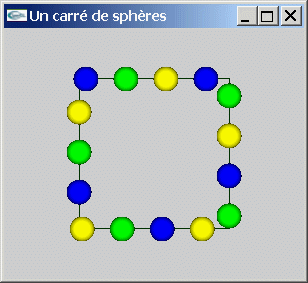
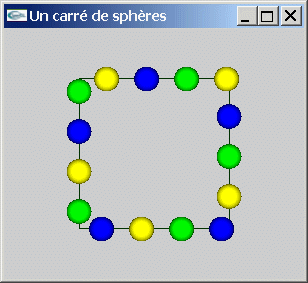
Fichier
source complet: CarreDeSpheres.cpp
Modules utilitaires: Modules.zip
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr