Correction
examen
de TD n°1 2004-2005
![]()
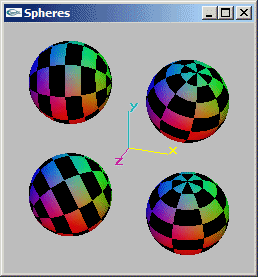
Question 1: Modélisation par facettes en OpenGL
La sphère est modélisée par un ensemble de facettes quadrangulaires se
recollant sur leurs bords en une surface facettisée. Cette surface facettisée est
fermée et donne l'illusion d'un volume. Les sommets sont générés par itération
uniforme sur les valeurs u et t de la formule dans leurs intervalles respectifs de
variabilité. La modélisation OpenGL est réalisée au moyen de QUAD_STRIP.
La fonction pourrait être optimisée car les sommets des pôles sont dupliqués alors
qu'ils pourraient ne pas l'être et les sinus et cosinus utilisés sont calculés
plusieurs fois alors qu'on pourrait les stocker dans un tableau.
Les normales utilisées sont les véritables normales calculée pour une sphère de rayon 1 centrée sur l'origine. Au point de coordonnées (x, y, z) d'une telle sphère, la normale extérieure est le vecteur de coordonnées (x, y, z).
Les coordonnées de texturage utilisées varient uniformément entre 0 et
1 pour chacun des deux axes en parallèle à la variation uniforme de u et t pour la
génération des sommets.
-> déformation de la texture aux poles.
Exam-TD1-2004-2005-Exo1
Fichier source complet : Exam-TD1-2004-2005-Exo1.cpp
Modules utilitaires: Modules.zip
Question 2: Bresenham pour le tracé de segments
La généralisation de l'algorithme de Bresenham nécessite de pouvoir:
- faire varier x en incrément de -1 ou de 1 (utilisation de la variable xinc),
- faire varier y en incrément de -1 ou de 1 (utilisation de la variable yinc),
- faire itérer sur y au lieu de x pour les segments "plus verticaux
qu'horizontaux" (deux portions de codes indépendantes ou les x et les y sont
permutés).
Exam-TD1-2004-2005-Exo2
Fichier source complet : Exam-TD1-2004-2005-Exo2.cpp
Modules utilitaires: Modules.zip
Question 3: Paramètrage de caméras en VRML
Le champs position définit la position de la caméra.
Par défaut, la caméra de visualisation en projection en perspective de VRML est orientée selon l'axe -z. Le champs orientation définit une rotation appliquée à cet axe permettant d'obtenir l'orientation souhaitée.
Le champs focalDistance est ignoré.
Le champs heightAngle définit la valeur d'ouverture verticale de la caméra. Il s'agit d'un angle en radian.
Premier point de vue
Depuis la position (0.0, 100.0, 0.0), la direction de visualisation (0.0, -1.0, 0.0) permet de "regarder" l'origine. Une rotation de -p/2 (-1.5708) radian autour de l'axe x (1.0, 0.0, 0.0) permet de transformer -z en -x.
Une valeur approximative de heightAngle peut être obtenue en divisant la
taille de l'objet visualisé par sa distance (si la taille est petite vis à vis de la
distance).
-> heightAngle = 20.0/100.0 = 0.2
On exploite ici la propriété qui veut atan(t/d) est voisin de t/d si t est petit par
rapport à d.
Second point de vue
Depuis la position (200.0, 200.0, 0.0), la direction de visualisation
(-1.0, -1.0, 0.0) permet de "regarder" l'origine. Une rotation de p/2 (1.5708) radian autour de l'axe x (-1.0, 1.0, 0.0) permet de
transformer (0.0, 0.0, -1.0) en (-1.0, -1.0, 0.0).
En effet:
- L'axe de rotation est l'axe orthogonal aux axes initial et final. Il est obtenu par
produit vectoriel entre ces deux axes.
- L'angle de rotation est l'angle entre les deux axes. Le cosinus de cet angle est égal
au produit scalaire entre l'axe initial normé et l'axe final normé. Ce calcul conduit à
la valeur 0 pour le produit scalaire (même sans normer) et donc à une valeur de p/2 (1.5708) radian.
heightAngle = 20.0/200.0/sqrt(2) = sqrt(2)/10.0 = 0.707
On exploite de nouveau la propriété qui veut atan(t/d) est voisin de t/d si t est petit
par rapport à d.
Exam-TD1-2004-2005-Exo3bv1.wrl
Une autre solution où l'on "tourne" de 180° (p radians) autour de l'axe bissecteur entre les directions (0.0, 0.0, -1.0) et (-1.0, -1.0, 0.0).
Exam-TD1-2004-2005-Exo3bv2.wrl
Question 4: Animation en OpenGL + GLUT
L'unique variable utilisée pour gérer l'animation est un compteur d'images.
Conception de la fonction idle
La fonction idle incrémente le compteur d'image et le replace à zéro
s'il dépasse le nombre total d'images à chaque tour le la sphère sur la trajectoire
carrée.
Elle demande ensuite l'affichage d'une nouvelle image.
Conception de la fonction display
Outre tous les appels de fonctions initiaux (effacement de la fenêtre de
dessin, empilement de la transformation courante) et finaux (dépilement de la
transformation courante, synchronisation de l'affichage, swap si un double-buffer est
utilisé) nécessaires à son fonctionnement, la fonction display modélise la scène.
Pour cela, elle utilise le compteur d'image pour calculer la distance parcouru par la
sphère sur sa trajectoire. Une fois cette distance connue et suivant sa valeur (dans les
intervalles [0.0, 5.0], [5.0, 10.0], [10.0, 15.0] ou [15.0, 20.0]), elle calcule la
position réelle de la sphère et s'en sert pour la dessinée après un glTranslatef.
Exam-TD1-2004-2005-Exo4
Fichier source complet : Exam-TD1-2004-2005-Exo4.cpp
Modules utilitaires: Modules.zip
![]()
Quelques indications sur l'évaluation
Tous les exercices sont affectés du même coefficient.
L'examen est trop long pour être réalisé en une durée de 1h20. Il est demandé aux
étudiants de réaliser correctement trois exercices sur quatre.
![]()
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr