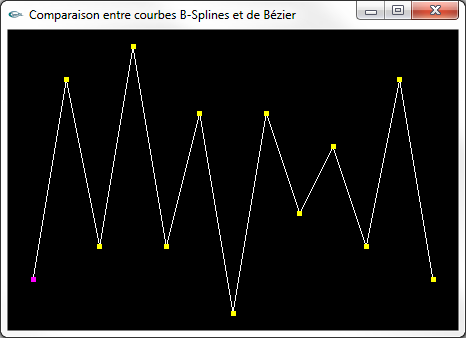
Ligne polygonale maîtresse

Ligne polygonale maîtresse
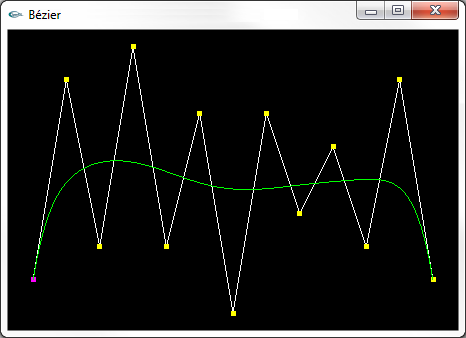
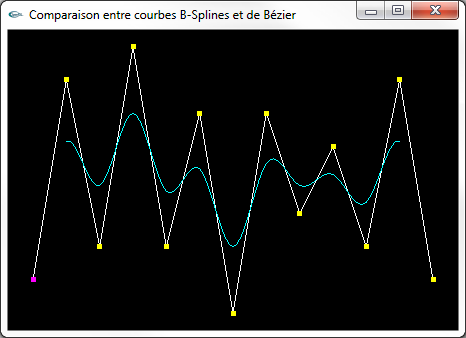

Courbes de Bézier, B-Spline NRU, spline de Catmull-Rom
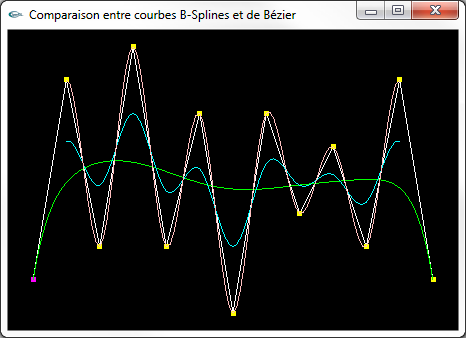
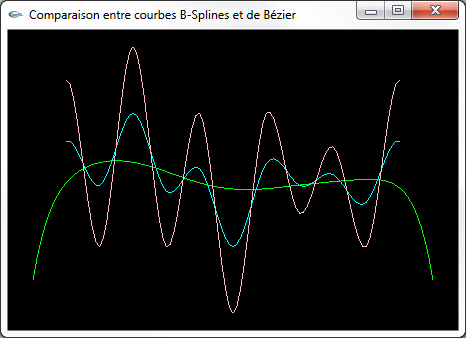
Courbes superposées
Le source : BezierBSplineComparaison.cpp
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Mars 2020 */
/* Comparaison entre courbe de Bézier */
/* et courbes BSplines generees */
/* sur les memes points de controle */
#include <math.h>
#include <stdlib.h>
#include <stdio.h>
#include <GL/glut.h>
#include <GL/gl.h>
#include <GL/glu.h>
#include "ModuleCouleurs.h"
#include "ModuleManipulateur.h"
#include "ModuleReshape.h"
struct coord_3D {
GLfloat x = 0.0F;
GLfloat y = 0.0F;
GLfloat z = 0.0F;
GLfloat w = 1.0F; };
struct lignePolygonale {
int n = 0;
coord_3D *p = NULL; };
typedef struct coord_3D coord_3D;
typedef struct lignePolygonale lignePolygonale;
typedef float matrice[4][4];
static GLfloat pts[13][4] = {
{ -12.0F,-6.0F, 4.0F, 1.0F },
{ -10.0F, 6.0F, 2.0F, 1.0F},
{ -8.0F,-4.0F,-2.0F, 1.0F},
{ -6.0F, 8.0F,-1.0F, 1.0F},
{ -4.0F,-4.0F, 0.0F, 1.0F},
{ -2.0F, 4.0F,-4.0F, 1.0F},
{ 0.0F,-8.0F, 1.0F, 1.0F},
{ 2.0F, 4.0F,-2.0F, 1.0F},
{ 4.0F,-2.0F, 4.0F, 1.0F},
{ 6.0F, 2.0F, 4.0F, 1.0F},
{ 8.0F,-4.0F,-2.0F, 1.0F},
{ 10.0F, 6.0F, 0.0F, 1.0F},
{ 12.0F,-6.0F, 4.0F, 1.0F}};
static int pt = 0;
static int mode = 0;
static int aff = 0;
static int pol = 3;
static int disc = 100;
static matrice matBSpline = { -0.1666666F, 0.5F, -0.5F, 0.1666666F,
0.5F ,-1.0F, 0.5F, 0.0F,
-0.5F , 0.0F, 0.5F, 0.0F,
0.1666666F, 0.6666666F, 0.1666666F,0.0F };
static matrice matCatmullRom = { -0.5F, 1.5F,-1.5F, 0.5F,
1.0F,-2.5F, 2.0F,-0.5F,
-0.5F, 0.0F, 0.5F, 0.0F,
0.0F, 1.0F, 0.0F, 0.0F};
static lignePolygonale pl;
static void point(float x,float y,float z) {
glVertex3f(x,y,z);
}
/* Trace un morceau de courbe B-Spline */
/* p est le tableau des 4 points de controle */
/* n est le nombre de points generes */
/* m est la matrice de base utilisee */
static void morceauBSpline(coord_3D *p,int n,matrice m) {
float tt[4],ttt[4],x,y,z ;
for ( int i = 0 ; i < n ; i++ ) {
float t =(float) i/(n-1) ;
tt[0] = t*t*t ;
tt[1] = t*t ;
tt[2] = t ;
tt[3] = 1.0F ;
for ( int j = 0 ; j < 4 ; j++ ) {
ttt[j] = 0.0F ;
for ( int k = 0 ; k < 4 ; k++ )
ttt[j] += tt[k] * m[k][j] ; }
x = y = z = 0.0F ;
for ( int j = 0 ; j < 4 ; j++ ) {
x += ttt[j] * p[j].x ;
y += ttt[j] * p[j].y ;
z += ttt[j] * p[j].z ; }
point(x,y,z) ; }
}
/* Trace une courbe B-Spline par morceaux */
/* m est la matrice de base utilisee */
/* p est la ligne polygonale lissee */
/* n est le nombre de points generes sur chacun */
/* des p->n-3 morceau traces */
/* ATTENTION : Les points de rattachement */
/* des morceaux de B-Spline sont generes deux fois. */
static void BSpline(lignePolygonale *p,matrice m,int n) {
for ( int i = 0 ; i < p->n-3 ; i++ )
morceauBSpline(&p->p[i],n,m) ;
}
/* Trace la courbe de Bezier formee de n points */
/* generee a partir de la ligne polygonale p */
static void bezier(lignePolygonale *p,int n) {
float x,y,z;
float *cn =(float *) calloc(p->n,sizeof(float));
cn[0] = 1;
cn[1] =(float) (p->n-1);
for ( int i = 2 ; i < p->n ; i++ )
cn[i] = cn[i-1] * (p->n - i) / i;
for ( int i = 0 ; i < n ; i++ ) {
float t =(float) i/(n-1);
float mt = 1.0F-t;
x = y = z = 0.0F;
for ( int j = 0 ; j < p->n ; j++ ) {
float fac = cn[j]*(float) pow(t,j)*
(float) pow(mt,p->n-1-j);
x += fac * p->p[j].x;
y += fac * p->p[j].y;
z += fac * p->p[j].z; }
point(x,y,z); }
free(cn);
}
static void afficheBezier(void) {
glColor4fv(couleurVert());
switch (aff) {
case 0 :
glBegin(GL_LINE_STRIP);
break;
case 1 :
glBegin(GL_POINTS);
break; }
bezier(&pl,disc);
glEnd();
}
static void afficheBSpline(void) {
glColor4fv(couleurCyan());
switch (aff) {
case 0 :
glBegin(GL_LINE_STRIP);
break;
case 1 :
glBegin(GL_POINTS);
break; }
BSpline(&pl,matBSpline,disc/10);
glEnd();
}
static void afficheCatmullRom(void) {
float roseClair[4] = { 1.0F,0.75F,0.75F,1.0F };
glColor4fv(roseClair);
switch (aff) {
case 0 :
glBegin(GL_LINE_STRIP);
break;
case 1 :
glBegin(GL_POINTS);
break; }
BSpline(&pl,matCatmullRom,disc/10);
glEnd();
}
static void display(void) {
int i;
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);
glPushMatrix();
manipulateurSouris();
manipulateurClavier();
if ( pol%2 == 1 ) {
glColor4fv(couleurBlanc());
glBegin(GL_LINE_STRIP);
for ( i = 0 ; i < pl.n ; i++ )
glVertex3fv((float *) &pl.p[i]);
glEnd(); }
if ( pol/2 == 1 ) {
glPointSize(5.0);
glBegin(GL_POINTS);
for ( i = 0 ; i < pl.n ; i++ ) {
glColor4fv((i == pt) ? couleurMagenta() : couleurJaune());
glVertex3fv((float *) &pl.p[i]); }
glEnd(); }
glPointSize(3.0);
switch (mode) {
case 1 :
afficheBezier();
break;
case 2 :
afficheBSpline();
break;
case 3 :
afficheCatmullRom();
break;
case 4 :
afficheBezier();
afficheBSpline();
afficheCatmullRom();
break; }
glPopMatrix();
glFlush();
glutSwapBuffers();
}
static void init(void) {
glClearColor(0.0,0.0,0.0,1.0);
}
static void special(int k, int x, int y) {
switch (k) {
case GLUT_KEY_LEFT : pts[pt][0] -= 0.1F;
glutPostRedisplay();
break;
case GLUT_KEY_RIGHT : pts[pt][0] += 0.1F;
glutPostRedisplay();
break;
case GLUT_KEY_UP : pts[pt][1] += 0.1F;
glutPostRedisplay();
break;
case GLUT_KEY_DOWN : pts[pt][1] -= 0.1F;
glutPostRedisplay();
break;
case GLUT_KEY_PAGE_UP : pts[pt][2] -= 0.1F;
glutPostRedisplay();
break;
case GLUT_KEY_PAGE_DOWN : pts[pt][2] += 0.1F;
glutPostRedisplay();
break; }
}
static void key(unsigned char key,int x,int y) {
if ( keyManipulateur(key,x,y) )
glutPostRedisplay();
else
switch ( key ) {
case 43 : disc++;
glutPostRedisplay();
break;
case 45 : disc--;
if ( disc < 3 )
disc = 3;
glutPostRedisplay();
break;
case 0x0D : mode = (mode+1)%5;
glutPostRedisplay();
break;
case 'a' : aff = (aff+1)%2;
glutPostRedisplay();
break;
case 'p' : pol = (pol+1)%4;
glutPostRedisplay();
break;
case ' ' : pt = (pt+1)%pl.n;
glutPostRedisplay();
break; }
}
int main(int argc,char **argv) {
pl.n = 13;
pl.p =(coord_3D *) &pts[0][0];
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_RGBA|GLUT_DEPTH|GLUT_DOUBLE);
glutInitWindowSize(450,300);
glutInitWindowPosition(50,50);
glutCreateWindow("Comparaison entre courbes B-Splines et de Bézier");
init();
setParametresOrthoBasique(-9.0,9.0,-9.0,9.0,-10.0,10.0);
setManipulateurDistance(1.0F);
glutReshapeFunc(reshapeOrthoBasique);
glutKeyboardFunc(key);
glutSpecialFunc(special);
glutMotionFunc(motionBasique);
glutMouseFunc(sourisBasique);
glutDisplayFunc(display);
glutMainLoop();
return(0);
}