

Le fichier xxx.wrl en visualisation telle qu'elle
-> On voit l'objet de l'intérieur.
| Rotation de -p/4 radians (-90°) autour de
l'axe x passant par la position de la caméra. -> La caméra "baisse" la tête. #VRML
V1.0 ascii |
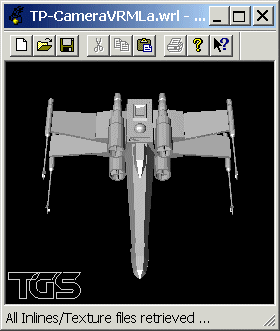 |
Exercice 1, question (b), version 1
| Rotation de 0.9553 radian autour de l'axe orthogonal: - à la direction de visualisation par défaut de la caméra (0.0, 0.0, -1.0) et - à la direction que doit adopter la caméra (-1.0, -1.0, -1.0). L'axe passe par la position de la caméra. On le calcule par produit vectoriel des deux directions (normées). L'angle q est l'angle entre les deux directions. Il est calculé par produit scalaire entre les deux directions (normées, cos(q) = produit scalaire). #VRML V1.0 ascii |
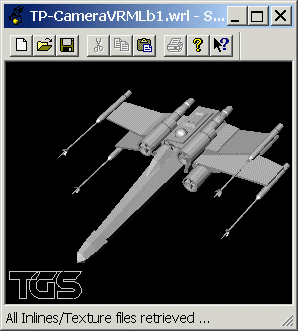 |
Exercice 1, question (b), version 2
| Rotation de p radian (180.0°)autour de l'axe
bissecteur: - à la direction de visualisation par défaut de la caméra (0.0, 0.0, -1.0) et - à la direction que doit adopter la caméra (-1.0, -1.0, -1.0). L'axe passe par la position de la caméra. On la calcule par somme des deux directions (normées). #VRML V1.0 ascii Tourner de 180.0° a pour conséquence l'obtention d'une image inversée. |
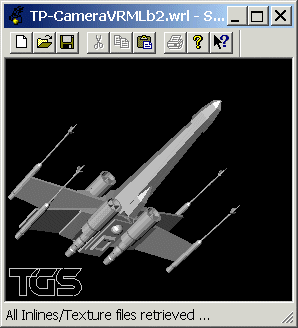 |
RETOUR