Algorithmique & Programmation
Semestre 2 ST
Algorithmes de recherche et de tri
Cours TD TP

 Problématique Recherche dans un tableau
sans organisation particulière		 Recherche
dans un tableau trié		 Tri naïf Tri par insertion 
Tri par sélection Tri à bulle Tri par fusion Quick sort Performances comparées

Version PDF

Clavier.class - Ecran.class - Documentation

Problématique

  • Traitements classiques de l'informatique:
    • Recherche d'une valeur dans un ensemble de valeurs
    • Tri d'un ensemble de valeurs selon un critère d'ordre total
  • Multiples algorithmes visant à assurer ces traitements de la manière la plus efficace possible
  • Choix entre telle ou telle méthode de traitement influencé par des critères tels que:
    • Rapidité intrinsèque de l'algorithme
    • Taille de l'ensemble de données
    • Possibilité particulière d'exploitation les caractéristiques propres de l'ensemble de données
    • Taille de l'empreinte mémoire (quantité de mémoire nécessaire au fonctionnement) associée à tel ou tel algorithme
    • Facilité d'implantation de l'algorithme
    • ...

Recherche dans un "tas" de données sans organisation particulière

  • Problème: Rechercher une donnée dans un ensemble non particulièrement organisé:
    • Test de présence
    • Recherche de minimum
    • Recherche de maximum
    • Recherche de l'occurrence d'une chaîne de caractères dans une autre chaîne de caractères
    • ...
  • Recherche de minimum dans un tableau
  • Algorithme naturel:
    • Utilisation d'une variable "minimum courant" pour stocker le minimum déjà trouvé
    • Initialisation de cette variable avec la première valeur du tableau
    • Parcours séquentiel complet du reste du tableau au moyen d'un "pour"
      • A chaque valeur parcourue, réaffectation du minimum courant avec la valeur en cours si celle-ci est plus petite que le minimum courant

{ Recherche de la valeur minimale               }
{ d'un tableau d'entiers                        }
{ sans organisation particuliere                }
{ Methode sequentielle                          }

constante entier N <- ...

entier fonction valeurMinimale(t)
  Donnees
    t : Tableau[N] de entier
  Locales
    i : entier
    min : entier
  min <- t[0]
  pour i de 1 à N-1 faire
    si t[i] < min alors
      min <- t[i]
    fsi
  fait
  retourner min
fin fonction

/* Methode de recherche de la valeur minimale    */
/* contenue dans un tableau de int               */

static int valeurMinimale(int [] t) {
  int i;
  int min;
  min = t[0];
  for ( i = 1 ; i < t.length ; i = i+1 ) {
    if ( t[i] < min ) {
      min = t[i]; } }
  return min;
}
RechercheMinimum.lda
RechercheMinimum.java
Exemple d'exécution
  • Test de présence
  • Algorithme intuitif:
    • Parcours séquentiel possiblement complet du tableau au moyen d'un "tant que"
      • A chaque valeur parcourue, si celle-ci est égale à la valeur recherchée, inutile d'aller plus loin car on l'a trouvée
        -> Retourner vrai
      • Parcours stoppé lorsque la dernière valeur du tableau a été traitée
        -> Retourner faux
  • Implantation
    • Utilisation d'une variable booléenne pour indiquer si la valeur recherchée a été trouvée
    • Initialisation de cette variable à faux car avant d'avoir commencer à chercher, on n'a pas trouvé
    • Parcours séquentiel au moyen d'un "tant que" pour que ce parcours puisse être complet mais aussi qu'il puisse être interrompu si la valeur recherchée a été trouvée
      -> Construction d'une expression conditionnelle non canonique

{ Recherche de la presence d'une valeur entiere }
{ dans un tableau d'entiers                     }
{ sans organisation particuliere                }
{ Methode sequentielle                          }

constante entier N <- ...

booleen fonction estPresent(v,t)
  Donnees
    v : entier
    t : Tableau[N] de entier
  Locales
    trouve : booleen
    i : entier
  trouve <- faux
  i <- 0
  tantque ( trouve = faux ) et ( i < N ) faire
    si t[i] = v alors
      trouve <- vrai
      sinon
      i <- i+1
    fsi
  fait
  retourner trouve
fin fonction

/* Methode de recherche de la presence           */
/*  d'une valeur entiere dans un tableau de int  */

static boolean estPresent(int v,int [] t) {
  boolean trouve;
  int i;
  trouve = false;
  i = 0;
  while ( ( trouve == false ) && ( i < t.length ) ) {
    if ( t[i] == v ) {
      trouve = true; }
      else {
      i = i+1; } }
  return trouve;
}
RecherchePresence.lda
RecherchePresence.java
Exemple d'exécution

Recherche dans un ensemble de données préalablement trié

  • Problème: Rechercher une donnée dans un ensemble de données trié
  • Optimisation des méthodes de recherche séquentielle utilisées dans les algorithmes présentés ci-dessus
  • Implantation d'algorithmes fonctionnant de manière différente
  • Recherche de la présence d'une valeur dans un tableau trié: Méthode séquentielle
  • Interruption possible de la recherche dès que la valeur recherchée respecte le critère de tri par rapport à l'élément courant du tableau
    • Reconception de l'algorithme pour utiliser une variable booléenne indiquant si la recherche doit être continuée ou non
    • Initialisation de cette variable à vrai
    • Parcours du tableau au moyen d'un "tant que" portant sur cette variable
    • Placement à faux si on arrive au bout du tableau ou, si ce n'est pas le cas, on trouve une valeur supérieure ou égale à la valeur recherchée.
        - Si égalité, on a trouvé donc on stoppe.
        - Si supériorité stricte, on ne pourra pas trouver donc on stoppe.

{ Recherche de la presence d'une valeur entiere }
{ dans un tableau d'entiers trie                }
{ par ordre croissant                           }
{ Methode sequentielle                          }

constante entier N <- ...

booleen fonction estPresent(v,t)
  Donnees
    v : entier
    t : Tableau[N] de entier
  Locales
    res : booleen
    run : booleen
    i : entier
  run <- vrai
  i <- 0
  tantque run = vrai faire
    si i = N alors
      run <- faux
      sinon
      si t[i] >= v alors
        run <- faux
        sinon
        i <- i+1
      fsi
    fsi
  fait
  res <- faux
  si i < N alors
    si t[i] = v alors
      res <- vrai
    fsi
  fsi
  retourner res
fin fonction

/* Recherche sequentielle de la presence         */
/* d'un int dans un tableau de int trie          */

static boolean estPresent(int v,int [] t) {
  boolean run;
  boolean res;
  int i;
  run = true;
  i = 0;
  while ( run ) {
    if ( i == t.length )
      run = false;
      else  {
      if ( t[i] >= v ) {
        run = false; }
        else {
        i = i+1; } } }
  res = false;
  if ( i < t.length ) {
    if ( t[i] == v ) {
      res = true; } }
  return res;
}

/* Recherche sequentielle de la presence         */
/* d'un int dans un tableau de int trie          */
/* Version optimisee                             */

static boolean estPresent2(int v,int [] t) {
  int i = 0;
  while ( ( i != t.length ) && ( t[i] < v ) ) {
    i = i+1; }
  return ( ( i < t.length ) && ( t[i] == v ) );
}
RecherchePresenceMethodeSequentielle.lda
RecherchePresenceMethodeSequentielle.java
Exemple d'exécution
  • Recherche de la présence d'une valeur dans un tableau trié: Méthode dichotomique
  • Diviser pour régner:
    • Exploitation de l'ordre existant pour minimiser le nombre d'étapes de la recherche et donc accélérer son exécution
  • Algorithme par méthode dichotomique:
    • Comparaison de la valeur médiane du tableau et de la valeur recherchée.
      Trois alternatives:
      • Egalité
      • Infériorité stricte
      • Supériorité stricte
    • Si égalité, présence de la valeur recherchée dans le tableau
      -> Inutile de continuer à chercher
      -> Retourner vrai
    • Si valeur recherchée plus petite
      -> Poursuite de la recherche dans le 1/2 tableau inférieur selon le même mode opératoire
    • Si valeur recherchée plus grande
      -> Poursuite de la recherche dans le 1/2 tableau supérieur selon le même mode opératoire
    • Quand retourner faux?
      Tableau réduit à zéro élément
  • Exemple: Soit le tableau de 15 valeurs entières dans lequel la valeur 16 est recherchée:
  • Indices de recherche: 0 et 14
10 12 12 15 16 18 21 23 23 25 28 29 31 33 36
  • Etape 1:
    • Indice de la valeur médiane: (0+14)/2 = 7
      -> Valeur médiane = 23
    • 23 différent de 16 et tableau non vide
      -> 23 plus grand que 16
      -> Sélection et poursuite sur le demi-tableau inférieur d'indice 0 à 7-1 = 6
10 12 12 15 16 18 21 23 23 25 28 29 31 33 36
  • Etape 2:
    • Indices de recherche: 0 et 6
    • Indice de la valeur médiane: (0+6)/2 = 3
      -> Valeur médiane = 15
    • 15 différent de 16 et tableau non vide
      -> 15 plus petit que 16
      -> Sélection et poursuite sur le demi-tableau supérieur d'indice 3+1 = 4 à 6
10 12 12 15 16 18 21 23 23 25 28 29 31 33 36
  • Etape 3:
    • Indices de recherche: 4 et 6
    • Indice de la valeur médiane est (4+6)/2 = 5
      -> Valeur médiane = 18
    • 18 différent de 16 et tableau non vide
      -> 18 est plus grand que 16
      -> Sélection et poursuite sur le demi-tableau inférieur d'indice 4 à 5-1 = 4
10 12 12 15 16 18 21 23 23 25 28 29 31 33 36
  • Etape 4:
    • Indices de recherche: 4 et 4
    • Indice de la valeur médiane est (4+4)/2 = 4
      -> Valeur médiane = 16
    • Valeur médiane égale valeur recherchée
      -> Arrêter et rendre vrai
  • Seulement 4 étapes de recherche au lieu d'au maximum 15 par la méthode séquentielle
  • Particularité de l'implantation de l'algorithme:
    • Pas d'extraction véritable des 1/2 tableaux
    • Gestion de deux variables indices indiquant respectivement les indices initiaux et finaux (inclus) du tableau en cours pour la recherche
    • Détection du fait que le tableau devient vide: L'indice initial devient supérieur strictement à l'indice final (égal à l'indice final+1).
  • Algorithme précis:
    • Soit une suite de n valeurs triée et stockée dans un tableau aux indices ii=0 à if=n-1
    • Réalisation du traitement suivant:
      • Si ii est strictement supérieur à if
        -> Suite vide
        -> Valeur recherchée non présente dans la suite
        -> Arrêter et retourner faux
      • Sinon trouver la valeur médiane vm à l'indice im=(ii+if)/2
        Si vm égale à la valeur recherchée
        -> Valeur trouvée!
        -> Arrêter et retourner vrai
      • Sinon si vm plus grande que la valeur recherchée
        -> Poursuite de la recherche dans la sous-suite restreinte aux valeurs d'indice ii à if=im-1
      • Sinon
        -> Poursuite de la recherche dans la sous-suite restreinte aux valeurs d'indice ii=im+1 à if

{ Recherche de la presence d'une valeur entiere }
{ dans un tableau d'entiers trie                }
{ par ordre croissant                           }
{ Methode dichotomique                          }

constante entier N <- ...

booleen fonction estPresent(v,t)
  Donnees
    v : entier
    t : Tableau[N] de entier
  Locales
    stop : booleen
    res : booleen
    indi : entier
    indf : entier
    indm : entier
    valm : entier
  res <- faux
  stop <- faux
  indi <- 0
  indf <- N-1
  tantque stop = faux faire
    si indi > indf alors
      stop <- vrai
      sinon
      indm <- (indi+indf)/2
      valm <- t[indm]
      si valm = v alors
        stop <- vrai
        res <- vrai
        sinon
        si v < valm alors
          indf <- indm-1
          sinon
          indi <- indm+1
        fsi
      fsi
    fsi
  fait
  retourner res
fin fonction

/* Recherche dichotomique de la presence         */
/* d'un int dans un tableau de int trie          */

static boolean estPresent(int v,int [] t) {
  boolean stop;
  boolean res;
  int indi;
  int indf;
  int indm;
  int valm;
  res = false;
  stop = false;
  indi = 0;
  indf = t.length-1;
  while ( stop == false ) {
    if ( indi > indf ) {
      stop = true; }
      else {
      indm = (indi+indf)/2;
      valm = t[indm];
      if ( valm == v ) {
        stop = true;
        res = true; }
        else {
        if ( v < valm ) {
          indf = indm-1; }
          else {
          indi = indm+1; } } } }
  return res ;
}
RecherchePresenceMethodeDichotomique.lda
RecherchePresenceMethodeDichotomique.java
Exemple d'exécution
  • Inconvénient de la recherche dichotomique: Complexité algorithmique (pas catastrophique)
  • Avantage de la recherche dichotomique: Grande rapidité par rapport à la recherche séquentielle
    • Algorithme séquentiel: Nombre d'itérations de l'ordre de la taille du tableau
    • Algorithme dichotomique: Division par deux (approximativement) de la taille de l'espace de recherche à chaque itération
      -> De l'ordre de log2(taille du tableau) itérations de recherche
    • Même si chaque itération est individuellement plus lourde car plus exigeante en traitements, au delà d'une certaine taille de tableau, l'algorithme dichotomique devient plus efficace en terme de temps de calcul.
      -> Augmentation rapide de l'avantage en terme de performance avec la taille des tableaux traités
Test de la vitesse d'exécution en recherche séquentielle et en recherche dichotomique
Tester avec 100000000 de recherches dans un ensemble trié de 10 valeurs,
10000000 de recherches dans un ensemble trié de 100 valeurs,
1000000 de recherches dans un ensemble trié de 1000 valeurs,
100000 de recherches dans un ensemble trié de 10000 valeurs,
10000 de recherches dans un ensemble trié de 100000 valeurs,
1000 de recherches dans un ensemble trié de 1000000 valeurs

Algorithme de tri naïf

  • Soit un ensemble de données E
  • Problème: Trier cet ensemble selon un critère d'ordre total
  • Algorithme naïf:
    • Créer un deuxième ensemble F vide mais capable de recevoir autant de données que E
    • Réalisation de n (n = cardinal(E)) fois le traitement:
      • Extraction de E de l'élément e restant qui est le plus "petit" selon le critère de tri
      • Déplacement de e de l'ensemble E vers la première position disponible en tête de l'ensemble F
  • Exemple: Tri par ordre décroissant d'un tableau de 10 entiers
  • Tableau initial
 E
16 15 12 10 12 15 19 18 10 16
F
--- --- --- --- --- --- --- --- --- ---
  • Etape 1: Sélection de l'entier 19
 E
16 15 12 10 12 15 19 18 10 16
  • Etape 1: Déplacement de 19 vers le tableau trié
 E
16 15 12 10 12 15 --- 18 10 16
19 --- --- --- --- --- --- --- --- ---
F
  • Etape 2: Sélection de l'entier 18
 E
16 15 12 10 12 15 --- 18 10 16
  • Etape 2: Déplacement de 18 vers le tableau trié
 E
16 15 12 10 12 15 --- --- 10 16
19 18 --- --- --- --- --- --- --- ---
F
  • Etape 3: Sélection de l'entier 16
 E
16 15 12 10 12 15 --- --- 10 16
  • Etape 3: Déplacement de 16 vers le tableau trié
 E
--- 15 12 10 12 15 --- --- 10 16
19 18 16 --- --- --- --- --- --- ---
F
  • Etape 4: Sélection de l'entier 16
 E
--- 15 12 10 12 15 --- --- 10 16
  • Etape 4: Déplacement de 16 vers le tableau trié
 E
--- 15 12 10 12 15 --- --- 10 ---
19 18 16 16 --- --- --- --- --- ---
F
  • Etape 5: Sélection de l'entier 15
 E
--- 15 12 10 12 15 --- --- 10 ---
  • Etape 5: Déplacement de 15 vers le tableau trié
 E
--- --- 12 10 12 15 --- --- 10 ---
19 18 16 16 15 --- --- --- --- ---
F
  • Etape 6: Sélection de l'entier 15
 E
--- --- 12 10 12 15 --- --- 10 ---
  • Etape 6: Déplacement de 15 vers le tableau trié
 E
--- --- 12 10 12 --- --- --- 10 ---
19 18 16 16 15 15 --- --- --- ---
F
  • Etape 7: Sélection de l'entier 12
 E
--- --- 12 10 12 --- --- --- 10 ---
  • Etape 7: Déplacement de 12 vers le tableau trié
 E
--- --- --- 10 12 --- --- --- 10 ---
19 18 16 16 15 15 12 --- --- ---
F
  • Etape 8: Sélection de l'entier 12
 E
--- --- --- 10 12 --- --- --- 10 ---
  • Etape 8: Déplacement de 12 vers le tableau trié
 E
--- --- --- 10 --- --- --- --- 10 ---
19 18 16 16 15 15 12 12 --- ---
F
  • Etape 9: Sélection de l'entier 10
 E
--- --- --- 10 --- --- --- --- 10 ---
  • Etape 9: Déplacement de 10 vers le tableau trié
 E
--- --- --- --- --- --- --- --- 10 ---
19 18 16 16 15 15 12 12 10 ---
F
  • Etape 10: Sélection de l'entier 10
 E
--- --- --- --- --- --- --- --- 10 ---
  • Etape 10: Déplacement de 10 vers le tableau trié
 E
--- --- --- --- --- --- --- --- --- ---
19 18 16 16 15 15 12 12 10 10
F
  • Inconvénient principal de cet algorithme: Pas d'optimisation de l'empreinte mémoire
    • Espace mémoire nécessaire au stockage de l'ensemble E + un espace mémoire équivalent pour stocker l'ensemble F

Exemple d'exécution

  • Implantation
  • Non décrite.

Buts visés par les algorithmes de tri classiques

  • Implantation d'une empreinte mémoire minimum: L'espace occupé par le tableau à trier + les (quelques) variables de gestion de l'algorithme
    -> Tri possible sans risque de dépassement de capacité mémoire disponible
  • Vitesse d'exécution "optimale"

Performances

  • A ne pas considérer en valeur absolue mais en valeur relative
  • Paramètres ayant une incidence directe sur la rapidité d'exécution:
    • Langage de programmation
    • Choix d'implantation
    • Puissance de l'ordinateur
    • Occupation de l'ordinateur
    • ...
  • Quatre types d'ensembles de données testés pour différentes tailles

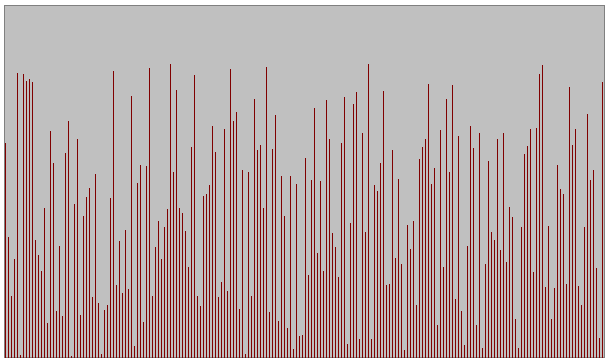
Série aléatoire

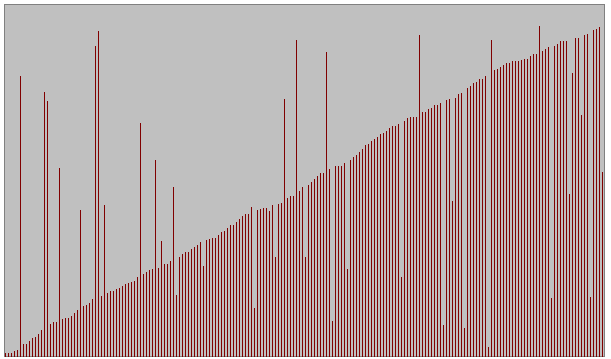
Série quasiment triée avec permutations entre éléments de n/10 couples quelconques
(n taille de l'ensemble)

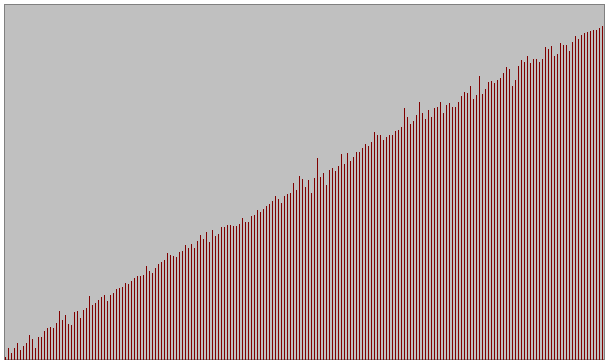
Série quasiment triée avec permutations entre les élements de n/10 couples de voisins
(n taille de l'ensemble)

Série déjà triée

Algorithme de tri par insertion

  • Tri par insertion: Algorithme naturellement utilisé par beaucoup de personnes lorsqu'un tri doit être réalisé (par exemple pour le tri d'un tas de cartes à jouer)
  • Soit un ensemble de données E
  • Problème: Trier cet ensemble selon un critère d'ordre total (i.e. tout couple de données est ordonnable selon le critère de tri)
  • Algorithme:
    • Réalisation n-1 (n = cardinal(E)) fois du traitement numéroté i (à partir de 0):
      • Extraction de E de l'élément e d'indice i+1
      • Insertion de e à sa place, selon la relation d'ordre du tri, dans la liste des éléments d'indice 0 à i (éléments déjà triés)
        • Une place libérée par l'élément d'indice i+1
          -> Décalage possible de toutes les données nécessaires à l'insertion à l'étape i
  • Exemple: Tri par ordre croissant d'un tableau de 10 entiers
  • Tableau initial
16 15 12 10 12 15 19 18 10 16
  • Etape 0: Insertion de 15 (indice 1) en position 0 dans la liste composée du seul élément d'indice 0
    -> Décalage de 16 vers la place libérée par le 15
16 15 12 10 12 15 19 18 10 16
15 16 12 10 12 15 19 18 10 16
  • Etape 1: Insertion de 12 (indice 2) en position 0 dans la liste composée des éléments d'indice 0 à 1
    -> Décalage des valeurs d'indice 0 à 1
15 16 12 10 12 15 19 18 10 16
12 15 16 10 12 15 19 18 10 16
  • Etape 2: Insertion de 10 (indice 3) en position 0 dans la liste composée des éléments d'indice 0 à 2
    -> Décalage des valeurs d'indice 0 à 2
12 15 16 10 12 15 19 18 10 16
10 12 15 16 12 15 19 18 10 16
  • Etape 3: Insertion de 12 (indice 4) en position 2 dans la liste composée des éléments d'indice 0 à 3
    -> Décalage des valeurs d'indice 2 à 3
10 12 15 16 12 15 19 18 10 16
10 12 12 15 16 15 19 18 10 16
  • Etape 4: Insertion de 15 (indice 5) en position 4 dans la liste composée des éléments d'indice 0 à 4
    -> Décalage de la valeur d'indice 4
10 12 12 15 16 15 19 18 10 16
10 12 12 15 15 16 19 18 10 16
  • Etape 5: Insertion de 19 (indice 6) en position 6 dans la liste composée des éléments d'indice 0 à 5
    -> Pas de décalage
10 12 12 15 15 16 19 18 10 16
10 12 12 15 15 16 19 18 10 16
  • Etape 6: Insertion de 18 (indice 7) en position 6 dans la liste composée des éléments d'indice 0 à 6
    -> Décalage de la valeur d'indice 6
10 12 12 15 15 16 19 18 10 16
10 12 12 15 15 16 18 19 10 16
  • Etape 7: Insertion de 10 (indice 8) en position 1 dans la liste composée des éléments d'indice 0 à 7
    -> Décalage des valeurs d'indice 1 à 7
10 12 12 15 15 16 18 19 10 16
10 10 12 12 15 15 16 18 19 16
  • Etape 8: Insertion de 16 (indice 9) en position 7 dans la liste composée des éléments d'indice 0 à 8
    -> Décalage des valeurs d'indice 7 à 8
    -> L'état final est atteint
10 12 12 12 15 15 16 18 19 16
10 10 12 12 15 15 16 16 18 19
  • Réservation d'un second tableau non nécessaire
  • Utilisation du seul espace mémoire supplémentaire utilisé pour l'opération d'insertion/décalage

Exemple d'exécution

  • Implantation

constante entier N <- ...

{ Methode de recherche de la position           }
{ d'un entier v dans un tableau d'entiers       }
{ restreint aux indices 0 a l-1                 }
{ (n premieres valeurs)                        }

entier fonction positionInsertion(v,l,t)
  Données
    v : entier
    l : entier
    t : Tableau [N] de entier
  Locales
    p : entier
  p <- l
  faire
    p <- p-1
  tant que ( ( p >= 0 ) et ( v < t[p] ) )
  p <- p+1
  retourner p
fin fonction

{ Methode de decalage de une cellule            }
{ vers la droite du contenu des cellules        }
{ de l'indice indi a l'indice indf inclus       }
{ d'un tableau d'entiers                        }

action decalage(indi,indf,t)
  Donnees / Resultat
    t : Tableau [N] de entier
  Données
    indi : entier
    indf : entier
  Locales
    i : entier
  pour i de indf à indi pas -1 faire
    t[i+1] <- t[i]
  fait
fin action

{ Methode de tri par insertion d'un tableau     }
{ d'entiers                                     }

action triInsertion(t)
  Donnees / Resultat
    t : Tableau [N] de entier
  Locales
    i : entier
    p : entier
    v : entier
  pour i de 1 à N-1 faire
    p <- positionInsertion(t[i],i,t)
    si p <> i alors
      v <- t[i]
      decalage(p,i-1,t)
      t[p] <- v
    fsi
  fait
fin action

/* Methode de recherche de la position           */
/* d'un entier v dans un tableau d'entiers       */
/* restreint aux indices 0 a l-1 inclus          */

static int positionInsertion(int v,int l,int [] t) {
  int p = l;
  do {
    p = p-1; }
  while ( ( p >= 0 ) && ( v < t[p] ) );
  p = p+1;
  return p;
}

/* Methode de decalage de une cellule            */
/* vers la droite du contenu des cellules        */
/* de l'indice indi a l'indice indf              */
/* d'un tableau d'entiers                        */

static void decalage(int indi,int indf,int [] t) {
  int i;
  for ( i = indf ; i >= indi ; i = i-1 ) {
    t[i+1] = t[i]; }
}

/* Methode de tri par insertion d'un tableau     */
/* d'entiers                                     */

static void triInsertion(int [] t) {
  int i;
  int p;
  int v;
  for ( i = 1 ; i < t.length ; i++ ) {
    p = positionInsertion(t[i],i,t);
    if ( p != i ) {
      v = t[i];
      decalage(p,i-1,t);
      t[p] = v; } }
}
TriInsertion.lda
TriInsertion.java
Exemple d'exécution
  • Performances
  • Quatre types d'ensembles de données testés pour différentes tailles:
    • Ensemble totalement aléatoire
    • Ensemble quasiment trié 1 (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)
    • Ensemble quasiment trié 2 (à partir de l'état trié, 10% de permutations entre voisins)
    • Ensemble déjà trié

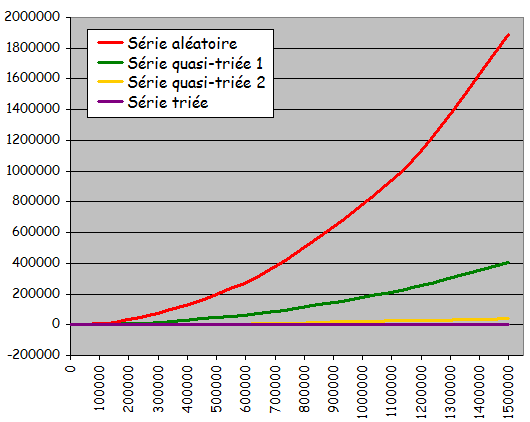
n Séries aléatoires Séries quasi-triées n°1 Séries quasi-triées n°2 Séries triées
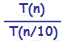
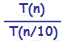
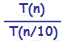
T(n) T(n) T(n) T(n)
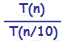
2 0,00000940 - 0,00000686 - 0,00001720 - 0,00000531 -
5 0,00004530 - 0,00001373 - 0,00004530 - 0,00000718 -
10 0,00021230 - 0,00007330 - 0,00012330 - 0,00003573 -
12 0,00028870 - 0,00008110 - 0,00013090 - 0,00004220 -
15 0,00037500 - 0,00013890 - 0,00016370 - 0,00006240 -
20 0,00062400 - 0,00026500 - 0,00021220 - 0,00010440 -
30 0,00129400 - 0,00057700 - 0,00034310 - 0,00015290 -
50 0,00312000 - 0,00085700 - 0,00046800 - 0,00022780 -
70 0,00520900 - 0,00187200 - 0,00059300 - 0,00029640 -
100 0,00968000 45,60 0,00281000 38,34 0,00125000 10,14 0,00041490 11,61
120 0,01358000 47,04 0,00407000 50,18 0,00219000 16,73 0,00057700 13,67
150 0,02059000 54,91 0,00701000 50,47 0,00266000 16,25 0,00067100 10,75
200 0,03479000 55,75 0,00967000 36,49 0,00249000 11,73 0,00095200 9,12
300 0,07020000 54,25 0,01996000 34,59 0,00608000 17,72 0,00116900 7,65
500 0,19960000 63,97 0,05320000 62,08 0,01202000 25,68 0,00198100 8,70
700 0,39010000 74,89 0,09840000 52,56 0,02231000 37,62 0,00290200 9,79
1000 0,79600000 82,23 0,19650000 69,93 0,03590000 28,72 0,00425900 10,27
1200 1,13420000 83,52 0,28550000 70,15 0,04680000 21,37 0,00497600 8,62
1500 1,77210000 86,07 0,42910000 61,21 0,07960000 29,92 0,00686000 10,22
2000 3,13710000 90,17 0,75050000 77,61 0,09990000 40,12 0,00827000 8,69
3000 7,11300000 101,32 1,64890000 82,61 0,21060000 34,64 0,01092000 9,34
5000 19,63900000 98,39 4,51780000 84,92 0,57410000 47,76 0,01810000 9,14
7000 37,91000000 97,18 8,86200000 90,06 1,04670000 46,92 0,02869000 9,89
10000 78,00000000 97,99 18,19000000 92,57 2,19800000 61,23 0,04009000 9,41
12000 113,80000000 100,34 26,36000000 92,33 2,80800000 60,00 0,04852000 9,75
15000 172,00000000 97,06 39,93000000 93,06 4,46200000 56,06 0,06230000 9,08
20000 310,40000000 98,94 72,23000000 96,24 7,80000000 78,08 0,08260000 9,99
30000 706,70000000 99,35 160,99000000 97,63 17,06700000 81,04 0,12180000 11,15
50000 1948,30000000 99,21 445,38000000 98,58 46,96000000 81,80 0,20900000 11,55
70000 3817,20000000 100,69 886,20000000 100,00 92,19000000 88,08 0,29010000 10,11
100000 7769,00000000 99,60 1815,80000000 99,82 187,98000000 85,52 0,42900000 10,70
120000 11232,00000000 98,70 2589,60000000 98,24 269,90000000 96,12 0,54600000 11,25
150000 17504,00000000 101,77 4009,30000000 100,41 422,80000000 94,76 0,60900000 9,78
200000 31184,00000000 100,46 7188,60000000 99,52 741,00000000 95,00 0,90500000 10,96
300000 70451,00000000 99,69 16036,00000000 99,61 1680,10000000 98,44 1,07700000 8,84
500000 194673,00000000 99,92 44615,00000000 100,17 4619,10000000 98,36 1,90400000 9,11
700000 380219,00000000 99,61 87734,00000000 99,00 9077,60000000 98,47 2,70000000 9,31
1000000 782387,00000000 100,71 179338,00000000 98,77 18443,90000000 98,12 4,30600000 10,04
1200000 1135432,00000000 101,09 258351,00000000 99,76 26707,00000000 98,95 5,10100000 9,34
1500000 1891596,00000000 108,07 405849,00000000 101,23 41511,00000000 98,18 6,05300000 9,94
  • Résultats expérimentaux:
    • Pour les ensembles aléatoires et les 2 ensembles quasi-triés:
      • Temps d'exécution "quadratique" quand la taille de l'ensemble à trier devient grande
        -> Temps de tri d'un ensemble n fois plus grand que l'ensemble E égal à n2 fois le temps de tri de E
        -> Mauvaise scalabilité
        • Trier un ensemble 2 fois plus grand prend 4 fois plus de temps
        • Trier un ensemble 10 fois plus grand prend 100 fois plus de temps
      • Pour une taille d'ensemble donnée, tri d'autant plus rapide qu'il est appliqué à des ensembles présentant un pré-tri important
    • Pour les ensembles déjà triés:
      • Exécution en temps linéaire et extrêmement rapide
      • Analyse du fonctionnement de l'algorithme:
        Dans ce cas particulier:
         - recherche de la position d'insertion très rapide car elle est trouvée tout de suite
         - jamais de décalage car toute valeur insérée le serait là où elle est déjà placée
            -> Pas d'insertion véritable
  • Amélioration de l'efficacité dans le cas général
    • Pas d'opération de décalage cellule après cellule pour toutes les cellules à décaler
    • Remplacement par:
      • Destruction de la cellule de stockage du tableau là où un élément disparait
      • Création, en position d'insertion, d'une autre cellule de stockage pour accueillir la valeur reportée
    • Pas possible sur les tableaux, possible avec des structures de données plus élaborées
  • Conclusion
    • Méthode intuitive
    • Bonne exploitation des caractéristiques des ensembles
    • Pas très simple à implanter

Algorithme de tri par sélection

  • Soit un ensemble de données E
  • Problème: Trier cet ensemble selon un critère d'ordre total (i.e. tout couple de données est ordonnable selon le critère de tri)
  • Algorithme de tri par sélection:
    • Réalisation n-1 (n = cardinal(E)) fois du traitement numéroté i:
      • Extraction de Ei (sous-ensemble de E limité à ses n-i premiers éléments) de l'indice de l'élément le plus "grand" selon le critère de tri
      • Permutation avec l'élément en queue de Ei
  • Exemple: Tri par ordre croissant d'un tableau de 10 entiers
  • Tableau initial
16 15 12 10 12 15 19 18 10 16
  • Etape 0: Sélection de 19 en indice 6 puis permutation avec l'élément d'indice 9
16 15 12 10 12 15 19 18 10 16
16 15 12 10 12 15 16 18 10 19
  • Etape 1: Sélection de 18 en indice 7 puis permutation avec l'élément d'indice 8
16 15 12 10 12 15 16 18 10 19
16 15 12 10 12 15 16 10 18 19
  • Etape 2: Sélection de 16 en indice 6 puis permutation avec l'élément d'indice 7
16 15 12 10 12 15 16 10 18 19
16 15 12 10 12 15 10 16 18 19
  • Etape 3: Sélection de 16 en indice 0 puis permutation avec l'élément d'indice 6
16 15 12 10 12 15 10 16 18 19
10 15 12 10 12 15 16 16 18 19
  • Etape 4: Sélection de 15 en indice 5 puis permutation avec l'élément d'indice 5 (pas de permutation)
10 15 12 10 12 15 16 16 18 19
10 15 12 10 12 15 16 16 18 19
  • Etape 5: Sélection de 15 en indice 1 puis permutation avec l'élément d'indice 4
10 15 12 10 12 15 16 16 18 19
10 12 12 10 15 15 16 16 18 19
  • Etape 6: Sélection de 12 en indice 2 puis permutation avec l'élément d'indice 3
10 12 12 10 15 15 16 16 18 19
10 12 10 12 15 15 16 16 18 19
  • Etape 7: Sélection de 12 en indice 1 puis permutation avec l'élément d'indice 2
10 12 10 12 15 15 16 16 18 19
10 10 12 12 15 15 16 16 18 19
  • Etape 8: Sélection de 10 en indice 1 puis permutation avec l'élément d'indice 1 (pas de permutation)
10 10 12 12 15 15 16 16 18 19
10 10 12 12 15 15 16 16 18 19
  • Etat final
10 10 12 12 15 15 16 16 18 19
  • Réservation d'un second tableau non nécessaire
  • Espace mémoire supplémentaire: Celui utilisé pour l'opération de permutation de deux entiers

Exemple d'exécution

  • Implantation

constante entier N <- ...

{ Methode de recherche de l'indice de la valeur }
{ maximale d'un tableau restreint               }
{ a ses n premieres valeurs                     }
  
entier fonction indiceMaximum(n,t)
  Données
    n : entier
    t : Tableau [N] de entier
  Locales
    max : entier
    iMax : entier
    i : entier
  max <- t[n]
  iMax <- n
  pour i de n-1 à 0 pas -1 faire
    si t[i] > max alors
      max <- t[i]
      iMax <- i
    fsi
  fait
  retourner iMax
fin action

{ Methode de tri par selection                  }
{ d'un tableau d'entiers                        }

action triSelection(t)
  Données / Résultats
    t : Tableau [N] de entier
  Locales
    i : entier
    aux : entier
    iMax : entier
  pour i de N-1 à 1 pas -1 faire
    iMax <- indiceMaximum(i,t)
    si iMax != i alors
      aux <- t[iMax]
      t[iMax] <- t[i]
      t[i] <- aux
    fsi
  fait
fin action

/* Methode de recherche de l'indice de la valeur */
/* maximale d'un tableau restreint               */
/* a ses n premieres valeurs                     */

static int indiceDuMaximum(int n,int [] t) {
  int max;
  int iMax;
  int i;
  max = t[n];
  iMax = n;
  for ( i = n-1 ; i >= 0 ; i = i-1 ) {
    if ( t[i] > max ) {
      max = t[i];
      iMax = i; } }
  return iMax;
}

/* Methode de tri par selection                  */
/* d'un tableau d'entiers                        */

static void triSelection(int [] t) {
  int i;
  int aux;
  int iMax;
  for ( i = t.length-1 ; i > 0 ; i = i-1 ) {
    iMax = indiceDuMaximum(i,t);
    if ( iMax != i ) {
      aux = t[iMax];
      t[iMax] = t[i];
      t[i] = aux; } }
}
TriSelection.lda
TriSelection.java
Exemple d'exécution
  • Performances
  • Quatre types d'ensembles de données testés pour différentes tailles:
    • Ensemble totalement aléatoire
    • Ensemble quasiment trié 1 (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)
    • Ensemble quasiment trié 2 (à partir de l'état trié, 10% de permutations entre voisins)
    • Ensemble déjà trié

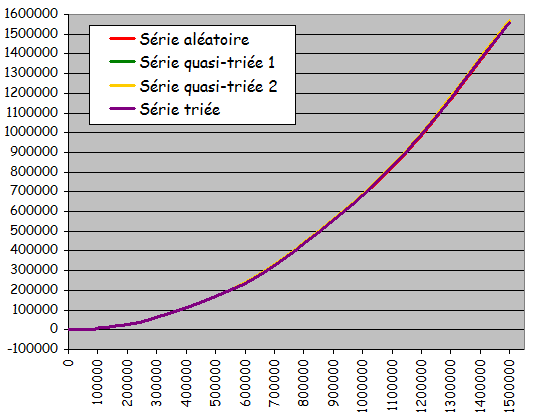
  • Résultats expérimentaux:
    • Temps quadratique fonction de la taille de l'ensemble à trier
    • Temps d'exécution très voisins pour les 4 types d'ensemble
    • Algorithme non intéressant si l'ensemble à trier peut éventuellement être déjà trié ou partiellement trié
  • Conclusion
    • Pas d'exploitation des caractéristiques des ensembles
    • Assez simple à implanter

Algorithme de tri à bulle

  • Basé sur l'opération consistant à permuter deux composantes
  • Soit un ensemble de données E
  • Problème: Trier cet ensemble selon un critère d'ordre total (i.e. tout couple de données est ordonnable selon le critère de tri)
  • Algorithme de tri à bulle:
    • Réalisation de n-1 (n = cardinal(E)) traitements numérotés i consistant à traiter le sous-ensemble Ei de E limité à ses n-i premières valeurs:
      • Parcours séquentiel des n-i-1 couples de valeurs contiguës de Ei
      • Permutation de ces deux valeurs si elles ne respectent pas le critère de tri
  • Exemple: Tri par ordre croissant d'un tableau de 10 entiers
  • Tableau initial
16 15 12 10 12 15 19 18 10 16
  • Etape 0: Parcours des 9 premiers couples d'entiers et permutation des 2 entiers s'ils ne sont pas correctement ordonnés (7 permutations)
16 15 12 10 12 15 19 18 10 16
15 16 12 10 12 15 19 18 10 16
15 12 16 10 12 15 19 18 10 16
15 12 10 16 12 15 19 18 10 16
15 12 10 12 16 15 19 18 10 16
15 12 10 12 15 16 19 18 10 16
15 12 10 12 15 16 19 18 10 16
15 12 10 12 15 16 18 19 10 16
15 12 10 12 15 16 18 10 19 16
15 12 10 12 15 16 18 10 16 19
15 12 10 12 15 16 18 10 16 19
  • Etape 1: Parcours des n-2 premiers couples (6 permutations)
12 10 12 15 16 15 10 16 18 19
  • Etape 2: Parcours des n-3 premiers couples (3 permutations)
10 12 12 15 15 10 16 16 18 19
  • Etape 3: Parcours des n-4 premiers couples (1 permutation)
10 12 12 15 10 15 16 16 18 19
  • Etape 4: Parcours des n-5 premiers couples (1 permutation)
10 12 12 10 15 15 16 16 18 19
  • Etape 5: Parcours des n-6 premiers couples (1 permutation)
10 12 10 12 15 15 16 16 18 19
  • Etape 6: Parcours des n-7 premiers couples (1 permutation)
10 10 12 12 15 15 16 16 18 19
  • Etape 7: Parcours des n-8 premiers couples (0 permutation)
10 10 12 12 15 15 16 16 18 19
  • Etape 8: Parcours des n-9 premiers couples (0 permutation)
10 10 12 12 15 15 16 16 18 19
  • Etat final
10 10 12 12 15 15 16 16 18 19

Exemple d'exécution

  • Implantation

constante entier N <- ...

{ Methode de tri a bulle d'un tableau d'entiers }

action triBulle(t)
  Données / Résultats
    t : Tableau [N] de entier
  Locales
    i : entier
    j : entier
    aux : entier
  pour i de 0 à N-2 faire
    pour j de 0 à N-2-i faire
      si t[j] > t[j+1] alors
        aux <- t[j]
        t[j] <- t[j+1]
        t[j+1] <- aux
      fsi
    fait
  fait
fin action

/* Methode de tri a bulle d'un tableau d'entiers */

static void triBulle(int [] t) {
  int i;
  int j;
  int aux;
  for ( i = 0 ; i < t.length-1 ; i = i+1 ) {
    for ( j = 0 ; j < t.length-i-1 ; j = j+1 ) {
      if ( t[j] > t[j+1] ) {
        aux = t[j];
        t[j] = t[j+1];
        t[j+1] = aux; } } }
}
TriBulle.lda
TriBulle.java
Exemple d'exécution
  • Optimisation
  • Optimisation classique de l'algorithme de tri à bulle:
    • Exploitation du fait qu'il n'est pas rare qu'il ne soit pas nécessaire d'effectuer n-1 étapes de recherche de permutations
    • Si, lors d'une étape, aucune permutation réalisée
      -> Tableau trié
      -> Plus nécessaire de continuer à chercher des permutations
      -> On arrête.

constante entier N <- ...

{ Methode de tri a bulle optimise               }
{ d'un tableau d'entiers                        }

action triBulleOptimise(t)
  Données / Résultats
    t : Tableau [N] de entier
  Locales
    i : entier
    j : entier
    aux : entier
    permutation : booleen
    ne : entier
    np : entier
    cpt : entier
  ne <- N-1
  np <- N-1
  cpt <- 0
  faire
    cpt <- cpt+1
    permutation <- faux
    pour j de 0 à np-1 faire
      si t[j] > t[j+1] alors
        aux <- t[j]
        t[j] <- t[j+1]
        t[j+1] <- aux
        permutation <- vrai
      fsi
    np <- np-1
  fait
  tantque permutation et ( cpt < ne )
fin action

/* Methode de tri a bulle optimise               */
/* d'un tableau d'entiers                        */

static void triBulleOptimise(int [] t) {
  int i;
  int j;
  int aux;
  boolean permutation;
  int ne = t.length-1;
  int np = t.length-1;
  int cpt = 0;
  do {
    cpt++;
    permutation = false;
    for ( j = 0 ; j < np ; j = j+1 ) {
      if ( t[j] > t[j+1] ) {
        aux = t[j];
        t[j] = t[j+1];
        t[j+1] = aux;
        permutation = true; } }
    np = np-1; }
  while ( permutation && ( cpt < ne ) ) ;
}
TriBulleOptimise.lda
TriBulleOptimise.java
Exemple d'exécution
  • Performances
  • Quatre types d'ensembles de données testés pour différentes tailles:
    • Ensemble totalement aléatoire
    • Ensemble quasiment trié 1 (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)
    • Ensemble quasiment trié 2 (à partir de l'état trié, 10% de permutations entre voisins)
    • Ensemble déjà trié


Tri à bulle sans optimisation


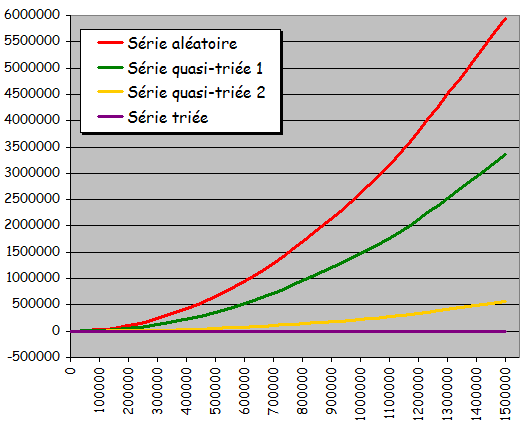
Tri à bulle avec optimisation

  • Résultats expérimentaux:
    • Temps quadratique de la taille de l'ensemble à trier
    • Exploitation d'une pré-organisation éventuelle de l'ensemble à trier pour accélérer le traitement
    • Version optimisée plus intéressante dans ce cadre (temps d'exécution quasi-instantané pour les ensembles triés)
  • Conclusion
    • Assez bonne exploitation des caractéristiques des ensembles
    • Très simple à implanter

Algorithme de tri par fusion

  • Algorithmes précédents gravement déficients:
    • Inadaptés au tri d'ensemble de données de cardinal très important
    • Pratiquement inemployables car trop lents au delà d'une certaine taille d'ensemble (temps quadratique de la taille de l'ensemble)
  • Existence d'une autre catégorie d'algorithmes de tri basée sur le réflexe naturel que nous avons tous quand il s'agit d'effectuer un tri sur un tas de données de taille importante:
    • Diviser le tas en 2 (ou plusieurs) tas élémentaires
    • Trier ces tas
    • Les fusionner de manière rapide en exploitant le fait qu'ils sont tous deux (tous) triés
  • Si subdivision en 2 tas -> Méthode dichotomique
  • Algorithme de tri par fusion:
    • Subdivision de l'ensemble E à trier en 2 sous-ensembles de tailles aussi identiques que possible
    • Tri de chacun des 2 sous-ensembles par le même algorithme
    • Fusion des deux sous-ensembles triés en un seul ensemble trié
  • Exemple: Tri par ordre croissant d'un tableau de 10 entiers
  • Tableau initial d'indices 0 à 9
16 15 12 10 12 15 19 18 10 16
  • Subdivision en 2 sous-tableaux d'indices 0 à 4 et 5 à 9
16 15 12 10 12 15 19 18 10 16
  • Subdivision du sous-tableau 0 à 4 en 2 sous-tableaux d'indices 0 à 1 et 2 à 4
  • Subdivision du sous-tableau 5 à 9 en 2 sous-tableaux d'indices 5 à 6 et 7 à 9
16 15 12 10 12 15 19 18 10 16
  • Le sous-tableau 0 à 1 a 2 valeurs. Soit il est déjà trié. Soit il ne l'est pas et on le trie en une permutation.
  • Subdivision du sous-tableau 2 à 4 en 2 sous-tableaux d'indices 2 à 2 et 3 à 4
  • Le sous-tableau 5 à 6 a 2 valeurs. Soit il est déjà trié. Soit il ne l'est pas et on le trie en une permutation.
  • Subdivision du sous-tableau 7 à 9 en 2 sous-tableaux d'indices 7 à 7 et 8 à 9
15 16 12 10 12 15 19 18 10 16
  • Le sous-tableau 0 à 1 est trié.
  • Le sous-tableau 2 à 2 est trié.
  • Le sous-tableau 3 à 4 a 2 valeurs. Soit il est déjà trié. Soit il ne l'est pas et on le trie en une permutation.
  • Le sous-tableau 5 à 6 est trié.
  • Le sous-tableau 7 à 7 est trié.
  • Le sous-tableau 8 à 9 a 2 valeurs. Soit il est déjà trié. Soit il ne l'est pas et on le trie en une permutation.

-> Tous les sous-tableaux sont triés.
-> On fusionne dans l'ordre inverse des subdivisions.
15 16 12 10 12 15 19 18 10 16
  • Fusion des sous-tableaux 2 à 2 et 3 à 4
  • Fusion des sous-tableaux 7 à 7 et 8 à 9
15 16 10 12 12 15 19 10 16 18
  • Fusion des sous-tableaux 0 à 1 et 2 à 4
  • Fusion des sous-tableaux 5 à 6 et 7 à 9
10 12 12 15 16 10 15 16 18 19
  • Etat final après fusion des sous-tableaux 0 à 4 et 5 à 9
10 10 12 12 15 15 16 16 18 19

Exemple d'exécution

  • Implantation
  • Implantation du tri par fusion pas spécialement complexe mais grandement facilitée par l'utilisation d'une méthode de programmation non encore abordée: la récursivité
  • Pas de description précise ici

constante entier N <- ...

{ Methode de fusion en un tableau trie          }
{ de deux sous-tableaux contigus                }
{ d'un tableau d'entiers                        }
{ Sous-tableau 1: t1 valeurs depuis l'indice i1 }
{ Sous-tableau 2: t2 valeurs au dela            }

action fusion(int [] t,int i1,int t1,int t2)
  Donnees / Resultat
    t : Tableau [N] de entier
  Donnees
    i1 : entier
    t1 : entier
    t2 : entier
  Locales
    deb : entier
    i2 : entier
    l : entier
    l1 : entier
    l2 : entier
    tf : Tableau [N] de entier
    i : entier
  deb <- i1
  i2 <- i1+t1
  l <- t1+t2
  l1 <- i1+t1
  l2 <- l1+t2
  pour i de 0 à l-1 faire
    si i1 = l1 alors
      tf[i] <- t[i2]
      i2 <- i2+1
      sinon
      si i2 = l2 alors
        tf[i] <- t[i1]
        i1 <- i1+1
        sinon
        si t[i1] < t[i2] alors
          tf[i] <- t[i1]
          i1 <- i1+1
          sinon
          tf[i] <- t[i2]
          i2 <- i2+1
        fsi
      fsi
    fsi
  fait
  pour i de 0 à l-1 faire
    t[deb+i] <- tf[i]
  fait
fin action

{ Methode de tri par fusion  d'un tableau       }
{ d'entiers des indices indi a indf compris     }

action triFusion(t,indi,indf)
  Donnees / Resultat
    t : Tableau [N] de entier
  Donnees
    indi : entier
    indf : entier
  Locales
    iMedian : entier
    aux : entier
  dans le cas de indf-indi
    1 :
      si t[indf] < t[indi] alors
        aux <- t[indi]
        t[indi] <- t[indf]
        t[indf] <- aux
      fsi
    autres cas :
      iMedian =(indi+indf)/2
      si indi != iMedian alors
        triFusion(t,indi,iMedian)
      fsi
      si iMedian+1 != indf alors
        triFusion(t,iMedian+1,indf)
      fsi
      fusion(t,indi,iMedian-indi+1,indf-iMedian)
  fcas
fin action

{ Methode de tri par fusion de l'ensemble       }
{ d'un tableau d'entiers                        }

action triFusion(int [] t)
  Donnees / Resultat
    t : Tableau [N] de entier
  triFusion(t,0,N-1)
fin action

/* Methode de fusion en un tableau trie          */
/* de deux sous-tableaux contigus                */
/* d'un tableau d'entiers                        */
/* Sous-tableau 1: t1 valeurs depuis l'indice i1 */
/* Sous-tableau 2: t2 valeurs au dela            */

static void fusion(int [] t,int i1,int t1,int t2) {
  int deb = i1;
  int i2 = i1+t1;
  int l = t1+t2;
  int l1 = i1+t1;
  int l2 = l1+t2;
  int [] tf = new int[l];
  int i;
  for ( i = 0 ; i < l ; i = i+1 ) {
    if ( i1 == l1 ) {
      tf[i] = t[i2];
      i2 = i2+1; }
      else {
      if ( i2 == l2 ) {
        tf[i] = t[i1];
        i1 = i1+1; }
        else {
        if ( t[i1] < t[i2] ) {
          tf[i] = t[i1];
          i1 = i1+1; }
          else {
          tf[i] = t[i2];
          i2 = i2+1; } } } }
  for ( i = 0 ; i < l ; i = i+1 ) {
    t[deb+i] = tf[i]; }
}

/* Methode de tri par fusion  d'un tableau       */
/* d'entiers des indices indi a indf compris     */

static void triFusion(int [] t,int indi,int indf) {
  int iMedian;
  int aux;
  switch ( indf-indi ) {
    case 0 :
      break;
    case 1 : {
      if ( t[indf] < t[indi] ) {
         aux = t[indi];
        t[indi] = t[indf];
        t[indf] = aux; } }
      break;
    default : {
      iMedian =(indi+indf)/2;
      triFusion(t,indi,iMedian);
      triFusion(t,iMedian+1,indf);
      fusion(t,indi,iMedian-indi+1,indf-iMedian); } }
}

/* Methode de tri par fusion de l'ensemble       */
/* d'un tableau d'entiers                        */

static void triFusion(int [] t) {
  triFusion(t,0,t.length-1);
}
TriFusion.lda
TriFusion.java
Exemple d'exécution
  • Performances
  • Quatre types d'ensembles de données testés pour différentes tailles:
    • Ensemble totalement aléatoire
    • Ensemble quasiment trié 1 (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)
    • Ensemble quasiment trié 2 (à partir de l'état trié, 10% de permutations entre voisins)
    • Ensemble déjà trié

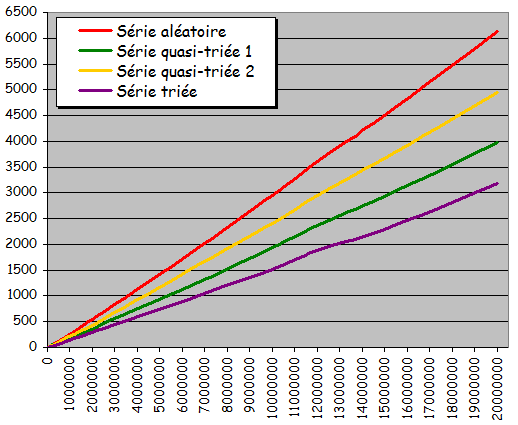
  • Résultats expérimentaux:
    • Courbes très différentes des courbes obtenues jusqu'ici pour les tris non dichotomiques:
      • Courbes non quadratiques
      • Forte ressemblance aux droites
      • Tri possible d'ensembles beaucoup plus grands en obtenant des temps d'exécution considérablement plus courts
    • Exploitation effective d'une pré-organisation de l'ensemble pour sensiblement accélérer le traitement

QuickSort

  • Algorithme du "QuickSort" (tri rapide) généralement employé quand il s'agit d'obtenir les meilleures performances
  • Basé sur le principe "diviser pour régner"
  • Technique de subdivision du QuickSort un peu plus élaborée que celle du tri par fusion
  • But: Eviter d'avoir à réaliser la phase de fusion
    • Ordonnement des sous-tableaux gauche et droit l'un par rapport à l'autre (i.e. la valeur "maximale" à gauche est plus "petite" que la valeur "minimale" à droite) avant de basculer vers la phase de tri de ces deux sous-tableaux
      -> Plus besoin de les fusionner
  • Phase de subdivision:
    • Détermination d'un pivot
    • Sélection de toutes les valeurs plus petites que le pivot et placement à gauche pour définir le sous-tableau gauche
    • Sélection de toutes les valeurs plus grandes que le pivot et placement à droite pour définir le sous-tableau droit
    • Nouvel indice de la valeur pivot: Limite entre les sous-tableaux gauche et droit
  • Utilisation de l'algorithme de tri sur les sous-tableaux gauche et droit pour les trier selon le même principe
  • Méthode de choix du pivot: Un des moyens offert au développeur pour optimiser le fonctionnement (éventuellement dans le cadre d'ensembles présentant certaines caractéristiques)
  • Techniques classiques:
    • Choisir la première valeur
    • Choisir la dernière valeur
    • Choisir la valeur d'indice médian
    • Choisir la moyenne des valeurs minimales et maximales du tableau
      • Pivot -> la valeur maximale du sous-tableau gauche et valeur minimale du sous-tableau droit

Exemple d'exécution

  • Implantation

constante entier N <- ...

{ Methode de reorganisation d'un tableau t      }
{ d'entiers des indices indi a indf inclus      }
{ par replacage a gauche de toutes les valeurs  }
{ plus petites que t[pivot], a droite de toutes }
{ les valeur plus grande que t[pivot]           }
{ et au centre de toutes les valeurs egales     }
{ a t[pivot]                                    }
{ Retourne l'indice de la valeur d'indice       }
{ maximum, apres replacage, de toutes           }
{ les valeurs egales a t[pivot]                 }

entier action pivotage(t,indi,indf,pivot)
  Donnees / Resultat
    t : Tableau [N] de entier
  Donnees
    indi : entier
    tndf : entier
    pivot : entier
  Locales
    aux : entier
    i : entier
    j : entier
  aux <- t[pivot]
  t[pivot] <- t[indf]
  t[indf] <- aux
  j <- indi
  pour i de indi à indf-1 faire
    si t[i] <= t[indf] alors
      aux <- t[i]
      t[i] <- t[j]
      t[j] <- aux
      j <- j+1
    fsi
  fait
  aux <- t[indf]
  t[indf] <- t[j]
  t[j] <- aux
  retourner j
fin action

{ Methode de tri par QuickSort d'un tableau     }
{ d'entiers des indices indi a indf compris     }
{ Pivot choisi a la valeur moyenne des valeurs  }
{ min et max                                    }

action triRapide(t,indi,indf)
  Donnees / Resultat
    t : Tableau [N] de entier
  Donnees
    indi : entier
    indf : entier
  Locales
    iMedian : entier
    aux : entier
    pivot : entier
  si indf = indi+1 alors
    si t[indf] < t[indi] alors
      aux <- t[indi]
      t[indi] <- t[indf]
      t[indf] <- aux
    fsi
    sinon
    pivot <- (indi+indf)/2
    iMedian <- pivotage(t,indi,indf,pivot)
    si iMedian > indi+1 alors
      triRapide(t,indi,iMedian-1)
    fsi
    si iMedian < indf-1 alors
      triRapide(t,iMedian+1,indf)
    fsi
  fsi
fin action

{ Methode de tri par QuickSort                  }
{ de l'ensemble d'un tableau d'entiers          }
{ Pivot choisi a la valeur moyenne des valeurs  }
{ min et max du tableau                         }

action triRapide(t)
  Données
    t : Tableau [N] de entier
  triRapide(t,0,N-1)
fin action

/* Methode de reorganisation d'un tableau t      */
/* d'entiers des indices indi a indf inclus      */
/* par replacage a gauche de toutes les valeurs  */
/* plus petites que t[pivot], a droite de toutes */
/* les valeur plus grande que t[pivot]           */
/* et au centre de toutes les valeurs egales     */
/* a t[pivot]                                    */
/* Retourne l'indice de la valeur d'indice       */
/* maximum, apres replacage, de toutes           */
/* les valeurs egales a t[pivot]                 */

static int pivotage(int [] t,int indi,int indf,int pivot) {
  int aux;
  int i;
  int j;
  aux = t[pivot];
  t[pivot] = t[indf];
  t[indf] = aux;
  j = indi;
  for ( i = indi ; i < indf ; i = i+1 ) {
    if ( t[i] <= t[indf] ) {
      aux = t[i];
      t[i] = t[j];
      t[j] = aux;
      j = j+1; } }
  aux = t[indf];
  t[indf] = t[j];
  t[j] = aux;
  return j;
}

/* Methode de tri par QuickSort d'un tableau     */
/* d'entiers des indices indi a indf compris     */
/* Pivot choisi a la valeur moyenne des valeurs  */
/* min et max                                    */

static void triRapide(int [] t,int indi,int indf) {
  int iMedian;
  int aux;
  int pivot;
  if ( indf == indi+1 ) {
    if ( t[indf] < t[indi] ) {
      aux = t[indi];
      t[indi] = t[indf];
      t[indf] = aux; } }
    else {
    pivot = (indi+indf)>>1;
    iMedian = pivotage(t,indi,indf,pivot);
    if ( iMedian > indi+1 ) {
      triRapide(t,indi,iMedian-1); }
    if ( iMedian < indf-1 ) {
      triRapide(t,iMedian+1,indf); } }
}

/* Methode de tri par QuickSort                  */
/* de l'ensemble d'un tableau d'entiers          */
/* Pivot choisi a la valeur moyenne des valeurs  */
/* min et max du tableau                         */

static void triRapide(int [] t) {
  triRapide(t,0,t.length-1);
}
TriRapide.lda
TriRapide.java
Exemple d'exécution
  • Performances
  • Quatre types d'ensembles de données testés pour différentes tailles:
    • Ensemble totalement aléatoire
    • Ensemble quasiment trié 1 (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)
    • Ensemble quasiment trié 2 (à partir de l'état trié, 10% de permutations entre voisins)
    • Ensemble déjà trié

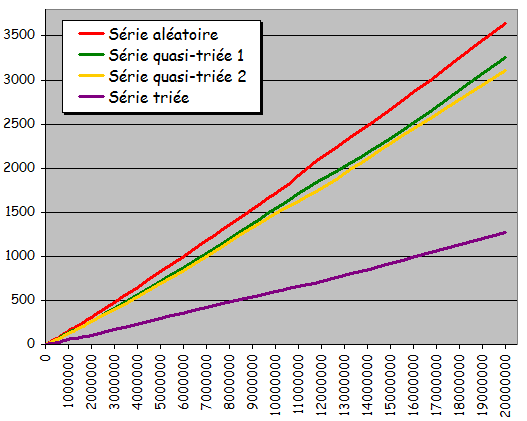
n Séries aléatoires Séries quasi-triées n°1 Séries quasi-triées n°2 Séries triées
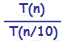
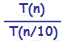
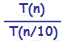
T(n) T(n) T(n) T(n)
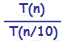
2 0,00000170 - 0,00000296 - 0,00000328 - 0,00000211 -
5 0,00005620 - 0,00002262 - 0,00005227 - 0,00001794 -
10 0,00025120 - 0,00012574 - 0,00015398 - 0,00007629 -
12 0,00032600 - 0,00016700 - 0,00021530 - 0,00010936 -
15 0,00044770 - 0,00020280 - 0,00028550 - 0,00016380 -
20 0,00065200 - 0,00039780 - 0,00045080 - 0,00024330 -
30 0,00113720 - 0,00073940 - 0,00070670 - 0,00040560 -
50 0,00218400 - 0,00137590 - 0,00127460 - 0,00074730 -
70 0,00330720 - 0,00217470 - 0,00196500 - 0,00117460 -
100 0,00508090 20,23 0,00346400 27,55 0,00338500 21,98 0,00181000 23,73
120 0,00652000 20,00 0,00455500 27,28 0,00394700 18,33 0,00247900 22,67
150 0,00814200 18,19 0,00608400 30,00 0,00546000 19,12 0,00310400 18,95
200 0,01154600 17,71 0,00809800 20,36 0,00776800 17,23 0,00432100 17,76
300 0,01940600 17,06 0,01404000 18,99 0,01224600 17,33 0,00717600 17,69
500 0,03494000 16,00 0,02489800 18,10 0,02268200 17,80 0,01282300 17,16
700 0,05118000 15,48 0,03755000 17,27 0,03433000 17,47 0,01862600 15,86
1000 0,07428000 14,62 0,05797000 16,73 0,05478000 16,18 0,02714000 14,99
1200 0,09360000 14,36 0,07160000 15,72 0,06270000 15,89 0,03478000 14,03
1500 0,11860000 14,57 0,09219000 15,15 0,08252000 15,11 0,04368000 14,07
2000 0,16660000 14,43 0,12917000 15,95 0,12044000 15,50 0,06193000 14,33
3000 0,26084000 13,44 0,20389000 14,52 0,18250000 14,90 0,09200000 12,82
5000 0,47740000 13,66 0,36005000 14,46 0,33860000 14,93 0,17320000 13,51
7000 0,68640000 13,41 0,54610000 14,54 0,52580000 15,32 0,24960000 13,40
10000 1,00470000 13,53 0,80040000 13,81 0,76130000 13,90 0,36040000 13,28
12000 1,21050000 12,93 0,98590000 13,77 0,93760000 14,95 0,41800000 12,02
15000 1,59110000 13,42 1,22160000 13,25 1,19350000 14,46 0,57720000 13,21
20000 2,20900000 13,26 1,71450000 13,27 1,57240000 13,06 0,76440000 12,34
30000 3,43510000 13,17 2,71600000 13,32 2,64260000 14,48 1,18560000 12,89
50000 5,94040000 12,44 4,75640000 13,21 4,61290000 13,62 2,05300000 11,85
70000 8,56290000 12,48 6,81800000 12,48 6,80100000 12,93 3,06380000 12,27
100000 12,60010000 12,54 10,20200000 12,75 10,07700000 13,24 4,38360000 12,16
120000 15,35050000 12,68 12,35500000 12,53 12,30800000 13,13 5,40080000 12,92
150000 19,26600000 12,11 16,09900000 13,18 15,58400000 13,06 6,89500000 11,95
200000 27,28500000 12,35 21,76200000 12,69 19,50000000 12,40 9,29140000 12,16
300000 40,57600000 11,81 33,99200000 12,52 32,30000000 12,22 14,57040000 12,29
500000 71,35500000 12,01 59,53000000 12,52 59,90000000 12,99 25,04120000 12,20
700000 102,83500000 12,01 86,10000000 12,63 82,99000000 12,20 36,00500000 11,75
1000000 149,99400000 11,90 126,99000000 12,45 121,36000000 12,04 52,93380000 12,08
1200000 181,14800000 11,80 155,53000000 12,59 148,20000000 12,04 65,00520000 12,04
1500000 227,15200000 11,79 196,87000000 12,23 189,60000000 12,17 77,61000000 11,26
2000000 310,12800000 11,37 264,73000000 12,16 260,55000000 13,36 106,70100000 11,48
3000000 478,48400000 11,79 413,41000000 12,16 397,85000000 12,32 168,64000000 11,57
5000000 824,68000000 11,56 718,37500000 12,07 688,75000000 11,50 289,54000000 11,56
7000000 1179,40900000 11,47 1033,52500000 12,00 1003,05000000 12,09 416,55000000 11,57
10000000 1717,32800000 11,45 1538,15000000 12,11 1482,00000000 12,21 606,05000000 11,45
12000000 2126,25900000 11,74 1870,42500000 12,03 1769,05000000 11,94 713,22000000 10,97
15000000 2663,34600000 11,72 2331,80000000 11,84 2276,80000000 12,01 916,32000000 11,81
20000000 3644,20000000 11,75 3250,25000000 12,28 3103,65000000 11,91 1273,75000000 11,94
  • Résultats expérimentaux
    • Courbes de temps d'exécution de même aspect linéaire que les courbes du tri par fusion (rassurant car même technique algorithmique)
    • Attention! Rapports T(n)/T(n/10) quasi-systématiquement supérieurs à 10.0
      -> Rapports peu compatibles avec l'hypothèse de linéarité car attendus voisins de 10.0 en cas de linéarité
    • Ici aussi, temps d'exécution raccourcis si pré-organisation de l'ensemble à trier

Performances comparées

  • Comparaison des temps d'exécution respectifs des différents algorithmes sur les différents ensembles testés
  • ATTENTION! A considérer avec prudence car de simples différences d'implantation des algorithmes pourraient avoir pour conséquence un changement des résultats et donc d'interprétation

Tris par insertion, par sélection, à bulle et à bulle optimisé

  • Séries aléatoires


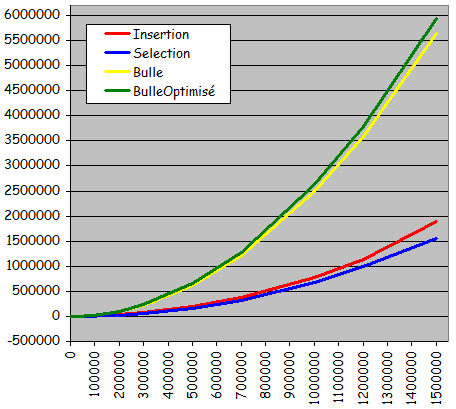
Temps de tri pour des séries totalement aléatoires

    • Tris par sélection et par insertion de performances voisines avec un léger avantage au tri par sélection
    • Tris à bulle sans et avec optimisation eux aussi de performances voisines avec un léger malus pour la version optimisée!
      Non compensation des calculs économisés par l'optimisation par les calculs consentis pour l'implantation de l'optimisation
    • Tris à bulle peu performants par rapport au 2 autres méthodes de tri: Près de 4 fois moins rapides
  • Séries quasi-triées (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)


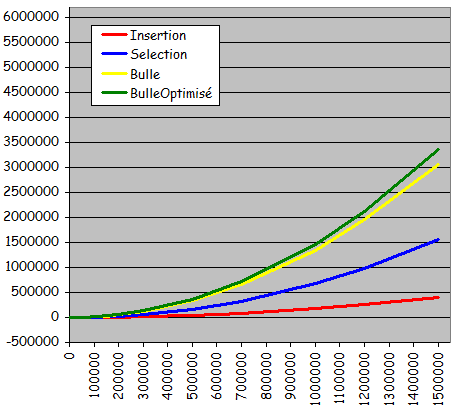
Temps de tri pour des séries quasi-triées
 (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)

    • Performances en progression sauf pour le tri par sélection qui reste inchangé
    • Le tri à bulle optimisé toujours non intéressant par rapport au tri à bulle sans optimisation
    • Le tri par insertion: Devient le plus rapide
  • Séries quasi-triées (à partir de l'état trié, 10% de permutations entre valeurs voisines)


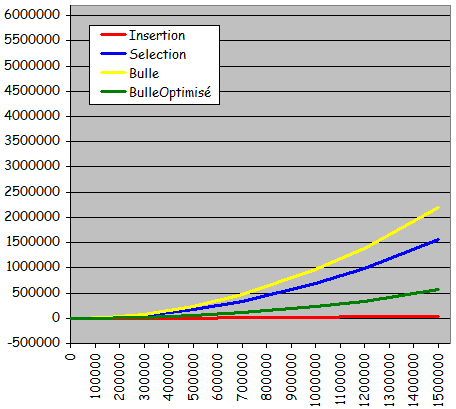
Temps de tri pour des séries quasi-triées
(à partir de l'état trié, 10% de permutations entre valeurs voisines)

    • Performances encore en progression sauf pour le tri par sélection (inchangé)
    • Tri à bulle optimisé très intéressant (c'est nouveau) par rapport au tri à bulle sans optimisation
    • Tri par insertion: Le plus rapide
  • Séries triées


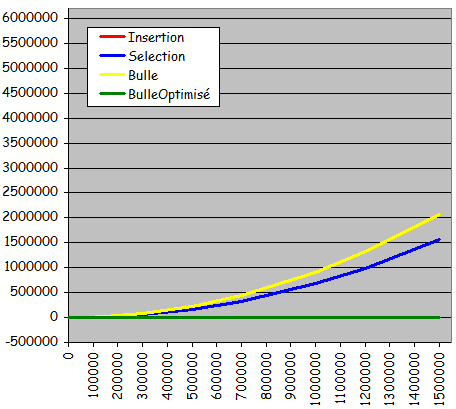
Temps de tri pour des séries triées

  • Tris par insertion et tri à bulle optimisé extrêmement rapides (détection très efficace du tri préexistant)
  • Accélération du tri à bulle mais de manière peu intéressante par rapport aux deux algorithmes précédents
  • Tri par sélection inchangé

Tri par fusion et tri rapide

  • Séries aléatoires


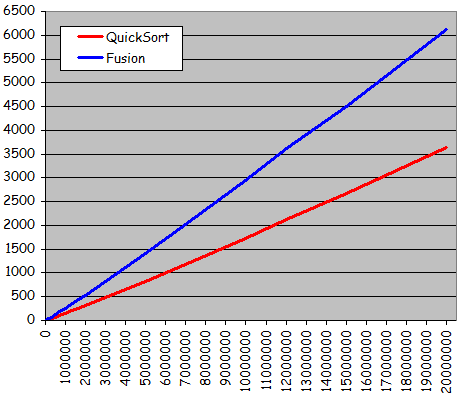
Temps de tri pour des séries totalement aléatoires

    • Tri rapide plus rapide que tri par fusion: Gain uniforme d'environ 40%
    • Courbes ressemblant à des droites
  • Séries quasi-triées (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)


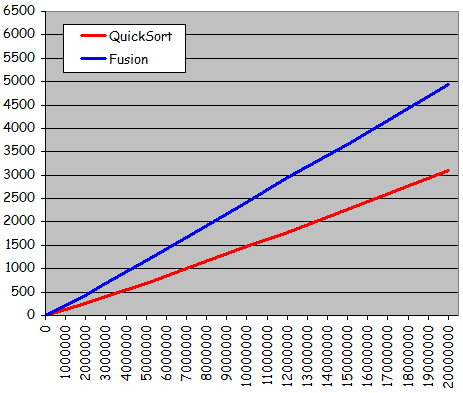
Temps de tri pour des séries quasi-triées
 (à partir de l'état trié, 10% de permutations entre valeurs d'indices quelconques)

    • Tri rapide toujours plus performant pour un gain d'environ 40%
  • Séries quasi-triées (à partir de l'état trié, 10% de permutations entre valeurs voisines)


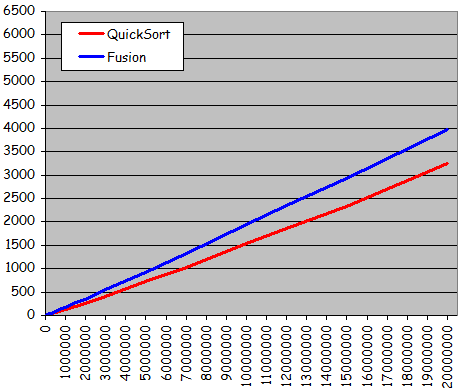
Temps de tri pour des séries quasi-triées
 (à partir de l'état trié, 10% de permutations entre valeurs voisines)

    • Tri rapide plus efficace que tri par fusion: Gain d'environ 20%
  • Séries triées


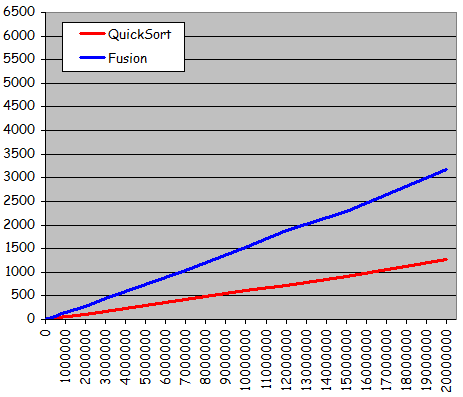
Temps de tri pour des séries triées

    • Tri rapide encore le plus rapide: Gain uniforme d'environ 60%
  • Pour de très grands ensembles de données, tri rapide toujours plus intéressant que le tri par fusion
    Intrinsèquement plus rapide et meilleure exploitation d'une éventuelle pré-organisation de l'ensemble à trier
  • Méthodes de tri dichotomiques incommensurablement supérieures aux méthodes de tri non dichotomiques quand utilisées sur de grands ensembles
  • Rapidité pour les ensembles de petite taille
  • Performances sur des suites aléatoires de petites tailles

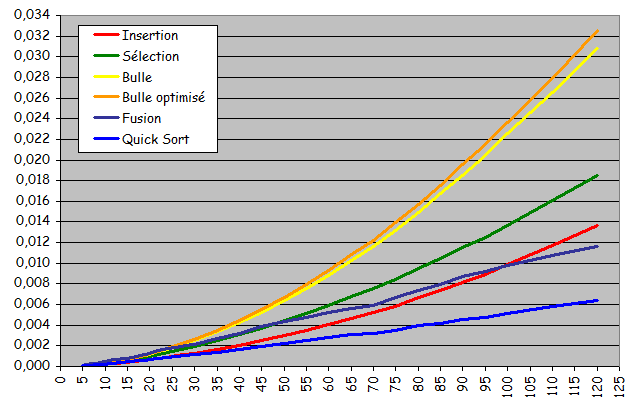
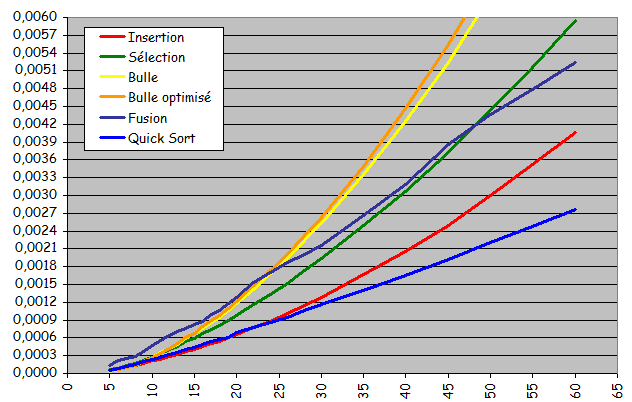
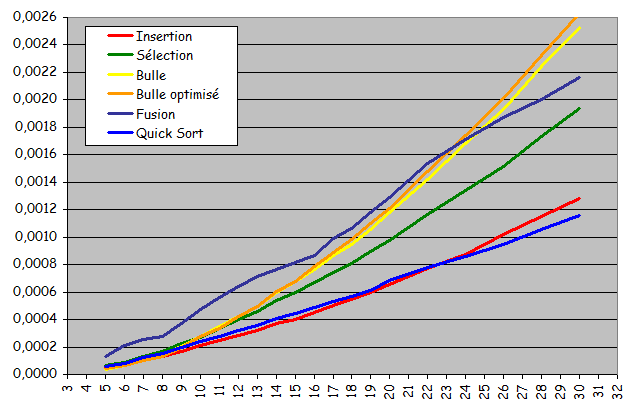
    • Tris rapide et par fusion assez rapidement (taille voisine de 100) les plus rapides
      (Ils le restent définitivement avec un avantage qui ne fait que croître)
    • Jusqu'à une taille voisine de 25, tris par insertion et rapide de performances voisines (léger avantage pour le tri par insertion)
    • Le tri rapide est "toujours" le plus rapide. Problème, c'est celui qui est le plus difficile à implanter.