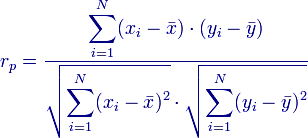|
Exercice n°1: Tableaux "simples"
a) On considère l'existence d'un tableau de réels. Ecrire un algorithme permettant de parcourir ce tableau pour afficher les valeurs qu'il
contient qui sont comprises entre une borne minimale et une borne maximale (bornes incluses).
|
AffichageTableauSeuils.lda
constante entier N <- ...
{ Fonction de création et retour }
{ d'un tableau de réels initialisé }
{ avec des nombres aléatoires }
{ compris entre 0.0 et 1.0 }
{ n : La taille du tableau à créer }
Tableau [] de réel fonction initRand(n)
Entrées
entier n
Locales
entier i
Tableau [n] de réel tab
pour i de 0 à n-1 faire
tab[i] <- random()
fait
retourner tab
fin fonction
{ Affichage d'un tableau de reels }
{ pour les valeurs comprises }
{ entre des bornes minimale et maximale }
action principale()
Locales
réel min
réel max
Tableau [N] de réel t
entier i
afficher("SVP, valeur minimale? ")
min <- saisir()
afficher("SVP, valeur maximale? ")
max <- saisir()
t <- initRand(N)
pour i de 0 à N-1 faire
si ( t[i] >= min ) et ( t[i] <= max ) alors
afficherln(t[i])
fsi
fait
fin action
Clavier.class - Ecran.class - Exemple d'exécution
|
b) On considère l'existence d'un tableau de réels. Ecrire un algorithme permettant de calculer et d'afficher la moyenne des valeurs contenues
dans ce tableau.
|
MoyenneTableau.lda
{ Action de remplissage d'un tableau de reels }
{ avec des nombres aleatoires }
{ compris entre 0.0 et 10.0 }
{ tab : Le tableau de réels à remplir }
action initRand(tab)
Sorties
Tableau [] de réel tab
Locales
entier i
pour i de 0 à longueur(tab)-1 faire
tab[i] <- random()*10.0
fait
fin action
{ Calcul de la moyenne des valeurs contenues }
{ dans un tableau de reels }
constante entier N <- ...
action principale()
Locales
entier i
reel moyenne
Tableau [N] de réel t
initRand(t)
moyenne <- 0.0
pour i de 0 à N-1 faire
moyenne <- moyenne+t[i]
fait
moyenne <- moyenne/N
afficherln("La moyenne est ",moyenne)
fin action
Clavier.class - Ecran.class - Exemple d'exécution
|
c) On considère l'existence d'un tableau de réels. Ecrire un algorithme permettant de déterminer et d'afficher le nombre de valeurs présentes dans
ce tableau qui sont inférieures ou égales à une valeur limite.
|
NombreValeursInferieuresLimite.lda
constante entier N <- ...
{ Fonction de création et retour }
{ d'un tableau de réels initialisé }
{ avec des nombres aleatoires }
{ compris dans l'intervalle [0.0,20.0[ }
{ n : La taille du tableau à créer }
Tableau [] de reel fonction initRand(n)
Entrées
entier n
Locales
entier i
Tableau [n] de reel tab
pour i de 0 à n-1 faire
tab[i] <- random()*20.0
fait
retourner tab
fin fonction
{ Calcul du nombre de valeurs inférieures }
{ ou egales a une valeur limite trouvees }
{ dans un tableau de reels }
action principale()
Locales
reel limite
Tableau [N] de reel t
entier i
entier cpt
t <- initRand(N)
afficher("SVP, valeur limite? ")
limite <- saisir()
cpt <- 0
pour i de 0 à N-1 faire
si t[i] <= limite alors
cpt <- cpt+1
fsi
fait
afficherln("Nombre valeurs < a ",limite,": ",cpt)
fin action
Clavier.class - Ecran.class - Exemple
d'exécution
|
d) On considère l'existence d'un tableau de réels. Les valeurs qu'il contient sont comprises dans l'intervalle [0.0, 20.0[. Ecrire
un algorithme permettant de calculer et d'afficher les nombres de valeurs de ce tableau comprises dans les intervalles [0.0,1.0[, [1.0, 2.0[,
[2.0, 3.0[, ..., [19.0, 20.0[ (classification).
|
ClassificationTableau.lda
{ Action de remplissage d'un tableau de reels }
{ initialise avec des nombres aleatoires }
{ compris dans l'intervalle [0.0,20.0[ }
{ tab : Le tableau de réels à remplir }
action initRand(tab)
Sorties
Tableau [] de reel tab
Locales
entier i
pour i de 0 à longueur(tab)-1 faire
tab[i] <- random()*20.0
fait
fin action
{ Calcul des nombres de de valeurs }
{ par intervalle de largeur 1.0 }
{ pour un tableau de reels compris }
{ entre 0.0 et 20.0 }
contante entier N <- ...
action principale()
Locales
Tableau [N] de reel t
Tableau [20] de entier classification
entier i
entier cl
initRand(t)
pour i de 0 à longueur(classification)-1 faire
classification[i] <- 0
fait
pour i de 0 à longueur(t)-1 faire
cl <- t[i]
classification[cl] <- classification[cl]+1
fait
afficherln("Nombres valeurs:")
pour i de 0 à longueur(classification)-1 faire
afficherln(i," ",classification[i])
fait
fin action
Clavier.class - Ecran.class - Exemple d'exécution
|
Exercice n°2: Tableaux en sous-algorithmes
a) Reprendre les questions (c) et (d) de l'exercice n°1 en les implantant avec utilisation de sous-algorithmes.
|
FonctionNombreValeursInferieuresLimite.lda
{ Fonction de calcul et retour du nombre }
{ de valeurs inférieures ou égales }
{ à une valeur limite trouvées }
{ dans un tableau de double }
{ t : Le tableau où est effectuée la recherche }
{ limite : La valeur limite de recherche }
entier fonction nbValeursInferieuresLimite(t,limite)
Entrées
Tableau [] de reel t
reel limite
Locales
entier cpt
entier i
cpt <- 0
pour i de 0 à longueur(t)-1 faire
si t[i] <= limite alors
cpt <- cpt+1
fsi
fait
retourner cpt
fin fonction
Clavier.class - Ecran.class - Exemple
d'exécution
|
|
FonctionClassificationTableau.lda
{ fonction de calcul des nombres de valeurs }
{ par intervalle de largeur 1.0 }
{ pour un tableau de reels compris }
{ dans l'intervalle [0.0,20.0[ }
{ et retour de ces valeurs dans un tableau }
{ t : Le tableau de réel de recherche }
Tableau [] de entier fonction classification(t)
Entrées
Tableau [] de reel t
Locales
entier i
entier cl
Tableau [20] de entier classification
pour i de 0 à longueur(classification)-1 faire
classification[i] <- 0
fait
pour i de 0 à longueur(t)-1 faire
cl <- t[i]
classification[cl] <- classification[cl]+1
fait
retourner classification
fin fonction
Clavier.class - Ecran.class - Exemple
d'exécution
|
b) Ecrire un sous-algorithme de recherche de l'indice de la valeur minimale contenue dans un tableau d'entiers.
|
IndiceDuMinimum.lda
{ Fonction de calcul et retour }
{ de l'indice de la valeur }
{ minimale d'un tableau d'entiers }
{ t : Le tableau de réel de recherche }
entier fonction indiceDuMinimum(t)
Entrées
Tableau [] de reel t
Locales
entier i
entier indice
indice <- 0
pour i de 1 à longueur(t)-1 faire
si t[i] < t[indice] alors
indice <- i
fsi
fait
retourner indice
fin fonction
Clavier.class - Ecran.class - Exemple d'exécution
|
c) Ecrire un sous-algorithme de fusion de deux tableaux d'entiers triés en un seul nouveau tableau d'entiers trié.
|
FusionTableaux.lda
{ Fonction de fusion de 2 tableau d'entiers }
{ triés en un nouveau tableau d'entiers trié }
{ et retour du tableau ainsi obtenu }
{ t1 : Le premier tableau d'entier }
{ t2 : Le second tableau d'entier }
Tableau [] de entier fonction fusion(t1,t2)
Entrées
Tableau [] de entier t1
Tableau [] de entier t2
Locales
entier n1 <- longueur(t1)
entier n2 <- longueur(t2)
Tableau [n1+n2] de entier t
entier i
entier i1
entier i2
i1 <- 0
i2 <- 0
pour i de 0 à n1+n2-1 faire
si i1 == n1 alors
t[i] <- t2[i2]
i2 <- i2+1
sinon
si i2 == n2 alors
t[i] <- t1[i1]
i1 <- i1+1
sinon
si t1[i1] < t2[i2] alors
t[i] <- t1[i1]
i1 <- i1+1
sinon
t[i] <- t2[i2]
i2 <- i2+1
fsi
fsi
fsi
fait
retourner t
fin fonction
Clavier.class - Ecran.class - Exemple d'exécution
|
Exercice n°3: Tableaux de variables de type agrégé
a) On considère le type agrégé sommet3D constitué des 3 champs x, y et z réels représentant une position dans un espace 3D. On considère un tableau
de n sommet3D.
Développer un sous-algorithme de calcul du barycentre d'un nuage de points stocké dans un tel tableau.
|
BarycentreNuageSommets3D.lda
{ Type agrege de stockage d'un sommet 3D }
structure sommet3D
reel x <- 0.0
reel y <- 0.0
reel z <- 0.0
fin structure
{ Fonction de calcul et retour du barycentre }
{ d'un nuage de points stocké dans un tableau }
{ de sommet3D }
{ tp : Le tableau de sommet3D }
sommet3D fonction barycentre(tp)
Entrées
Tableau [] de sommet3D tp
Locales
sommet3D p
entier i
pour i de 0 à longueur(tp)-1 faire
p.x <- p.x+tp[i].x
p.y <- p.y+tp[i].y
p.z <- p.z+tp[i].z
fait
p.x <- p.x/N
p.y <- p.y/N
p.z <- p.z/N
retourner p
fin fonction
Clavier.class - Ecran.class - Exemple d'exécution
|
b) On considère le type agrégé sommet2D constitué des 2 champs x et y réels représentant l'abscisse et l'ordonnée d'une position du plan.
On considère un tableau de n sommet2D.
1) Développer un sous-algorithme de création d'un tableau de sommet2D initialisé avec les positions des n sommets d'un polygone régulier
de rayon r.
2) Développer un sous-algorithme de calcul de la longueur d'une ligne polygonale non fermée stockée dans un tel tableau.
3) Développer un sous-algorithme de calcul de la longueur d'une boucle polygonale (fermée) stockée dans un tel tableau.
|
TableauSommets2D.lda
constante reel PI <- 3.14159
{ Type agrege de stockage d'un sommet 2D }
structure sommet2D
reel x <- 0.0
reel y <- 0.0
fin structure
{ Action de remplissage d'un tableau }
{ de sommet2D initialisé avec les positions }
{ des sommets d'un polygone regulier }
{ centre sur l'origine et de rayon r }
{ r : Le rayon du polygone régulier }
{ t : Le tableau de sommet2D à remplir }
action polygoneRegulier(r,t)
Entrées
reel r
Entrées / Sorties
Tableau [] de sommet2D t
Locales
i entier
reel angle
pour i de 0 à longueur(t)-1 faire
angle <- i*2.0*PI/longueur(t)
t[i].x <- r*cos(angle)
t[i].y <- r*sin(angle)
fait
fin action
{ Fonction de calcul et retour de la distance }
{ entre deux sommet2D }
{ p1 : Le premier sommet2D }
{ p2 : Le second sommet2D }
reel fonction distance(p1,p2)
Entrées
sommet2D p1
sommet2D p2
Locales
réel l
réel dx
réel dy
dx <- p2.x-p1.x
dy <- p2.y-p1.y
l <- sqrt(dx*dx+dy*dy)
retourner l
fin fonction
{ Fonction de calcul et retour de la longueur }
{ d'une ligne polygonale ouverte stockee }
{ dans un tableau de sommet2D }
{ t : Le tableau de sommet2D définissant }
{ la ligne polygonale }
reel fonction longueurLigne(t)
Entrées
Tableau [] de sommet2D t
Locales
reel l
entier i
l <- 0.0
pour i de 0 à longueur(t)-2 faire
l <- l+distance(t[i],t[i+1])
fait
retourner l
fin fonction
{ Fonction de calcul et retour de la longueur }
{ d'une boucle polygonale stockee }
{ dans un tableau de sommet2D }
{ t : Le tableau de sommet2D définissant }
{ la boucle polygonale }
reel fonction longueurBoucle(t)
Entrées
t Tableau [] de sommet2D
Locales
l réel
l <- longueurLigne(t) + distance(t[0],t[longueur(t)-1])
retourner l
fin fonction
Clavier.class - Ecran.class - Exemple d'exécution
|
Exercice n°4: Type agrégé avec tableau
a) On souhaite calculer le coefficient de corrélation linéaire défini entre deux séries de 15 données réelles.
1) Définir un type agrégé permettant de stocker ces deux séries de données en une seule variable.
2) Implanter un sous-algorithme permettant de calculer le coefficient de corrélation linéaire existant entre les deux séries de données stockées
au sein d'une variable du type agrégé de la question (1). On utilisera la formule de calcul suivante (wikipedia):
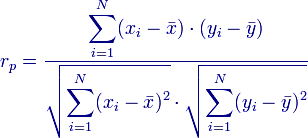
|
CoefficientCorrelationLineaire.lda
constante entier N <- 15
{ Type agrege de stockage de deux tableaux }
{ de 15 double }
structure DeuxSeries
Tableau [N] de reel x
Tableau [N] de reel y
fin structure
{ Fonction de calcul et retour de la moyenne }
{ des valeurs contenues dans un tableau }
{ de double }
{ t : Le tableau de calcul }
réel fonction moyenne(t)
Entrées
Tableau [] de réel t
Locales
reel moyenne
entier i
moyenne <- 0.0
pour i de 0 à longueur(t)-1 faire
moyenne <- moyenne+t[i]
fait
moyenne <- moyenne/N
retourner moyenne
fin fonction
{ Fonction de calcul et retour de l'ecart }
{ quadratique des valeurs contenues }
{ dans un tableau de double }
{ t : Le tableau de calcul }
{ m : La valeur par rapport à laquelle }
{ le calcul est réalisé }
réel fonction ecartQuadratique(t,m)
Entrées
Tableau [] de réel t
réel m
Locales
réel v
entier i
v <- 0.0
pour i de 0 à longueur(t)-1 faire
v <- v + (t[i]-m)*(t[i]-m)
fait
v <- sqrt(v)
retourner v
fin fonction
{ Fonction de calcul et retour du coefficient }
{ de correlation lineaire existant }
{ entre deux series de valeurs reelles }
{ ds : Le paramètre de type deuxSeries }
{ dans lequel sont stockées }
{ les deux séries }
réel fonction coefficientCorrelation(ds)
Entrées
deuxSeries ds
Locales
réel cc
entier i
réel mx
réel my
réel eqmx
réel eqmy
mx <- moyenne(ds.x)
my <- moyenne(ds.y)
cc <- 0.0
pour i de 0 à N-1 faire
cc <- cc + (ds.x[i]-mx)*(ds.y[i]-my)
fait
eqmx <- ecartQuadratique(ds.x,mx)
eqmy <- ecartQuadratique(ds.y,my)
cc <- cc/(eqmx*eqmy)
retourner cc
fin fonction
Clavier.class - Ecran.class - Exemple
d'exécution
|
b) On souhaite implanter une "structure de données" permettant de stocker un ensemble de chaînes de caractères pour un maximum de 20 chaînes
de caractères.
1) Définir un type agrégé permettant de stocker un tel ensemble (initialisé à l'ensemble vide).
2) Implanter un sous-algorithme permettant d'afficher les chaînes de caractères présentes dans un ensemble de chaînes de caractères.
3) Implanter un sous-algorithme permettant d'ajouter une chaîne de caractères à un ensemble de chaînes de caractères (l'ajout d'une
chaîne existant déjà est autorisé).
4) Implanter un sous-algorithme permettant de tester si une chaîne de caractères appartient à un ensemble de chaînes de caractères.
5) Implanter un sous-algorithme permettant de fusionner 2 ensembles de chaînes de caractères en un nouvel ensemble de chaînes de caractères.
6) Implanter un sous-algorithme permettant de retirer une chaîne de caractères d'un ensemble de chaînes de caractères.
7) Implanter un sous-algorithme permettant de tester si un ensemble de chaînes de caractères est vide.
|
EnsembleDeChainesDeCaracteres.lda
constante entier N <- 20
{ Type agrege de stockage d'un ensemble }
{ d'au maximum 20 chaines de caracteres }
structure ensembleDeChaines
entier n <- 0
Tableau [N] de chaine s
fin structure
{ Action d'affichage des chaines }
{ de caracteres contenues dans un ensemble }
{ de chaines de caracteres }
{ edc : L'ensembleDeChaines à afficher }
action affichage(edc)
Entrées
ensembleDeChaines edc
Locales
entier i
pour i de 0 à edc.n faire
afficherln(edc.s[i])
fait
fin action
{ Fonction d'ajout d'une chaine de caracteres }
{ à un ensemble de chaines de caracteres }
{ Retourne vrai si l'ajout a abouti }
{ Retourne faux si plus de place }
{ e : L'ensembleDeChaines où l'ajout }
{ est effectué }
{ s : La chaine ajoutée }
booleen fonction ajout(e,s)
Entrées / Sorties
ensembleDeChaines e
Entrées
chaine s
Locales
res booleen
si e.n < N alors
e.s[e.n] <- s
e.n <- e.n+1
res <- vrai
sinon
res <- faux
fsi
retourner res
fin fonction
{ Fonction de test de l'appartenance }
{ d'une chaine de caracteres }
{ a un ensemble de chaines de caracteres }
{ Retour de vrai si present, faux sinon }
{ e : L'ensembleDeChaines où la recherche }
{ est effectuée }
{ s : La chaine recherchée }
booleen fonction appartient(e,s)
Entrées
ensembleDeChaines e
chaine s
Locales
booleen res
i entier
res <- faux
i <- 0
tantque ( res == faux ) et ( i < e.n ) faire
res <- (e.s[i] == s)
i <- i+1
fait
retourner res
fin fonction
{ Action de fusion de deux ensembles }
{ de chaines de caracteres dans un ensemble }
{ de chaines de caracteres }
{ Retour de faux si fusion impossible }
{ car pas assez de place et ne touche pas }
{ au parametre en sortie }
{ Retour de vrai sinon }
{ e1 : Le premier ensembleDeChaines }
{ e2 : Le premier ensembleDeChaines }
{ e : L'ensembleDeChaines issu de la fusion }
booleen fonction fusion(e1,e2,e)
Entrées
ensembleDeChaines e1
ensembleDeChaines e2
Sorties
ensembleDeChaines e
Locales
entier i
booleen res
si e1.n+e2.n <= N alors
e.n <- 0
pour i de 0 à e1.n-1 faire
ajout(e,e1.s[i])
fait
pour i de 0 à e2.n-1 faire
ajout(e,e2.s[i])
fait
res <- vrai
sinon
res <- faux
fsi
retourner res
fin fonction
{ Fonction de retrait d'une chaine }
{ de caracteres a un ensemble de chaines }
{ de caracteres }
{ Retour de vrai si le retrait a abouti }
{ Retour de faux sinon }
{ e : L'ensembleDeChaines où le retrait }
{ est réalisé }
{ s : La chaine retirée }
booleen fonction retrait(e,s)
Entrées / Sorties
ensembleDeChaines e
Entrées
chaine s
Locales
booleen res
entier i
res <- faux
i <- 0
tantque ( res == faux ) et ( i < e.n ) faire
res <- (e.s[i] == s)
i <- i+1
fait
si res alors
pour i de i à e.n-1 faire
e.s[i-1] <- e.s[i]
fait
e.n <- e.n-1
fsi
retourner res
fin fonction
{ Fonction de test si un ensemble de chaines }
{ de caracteres est vide }
{ Retour de vrai si c'est le cas, faux sinon }
{ e : L'ensembleDeChaines testé }
booleen fonction estVide(e)
Données
ensembleDeChaines e
retourner (e.n == 0)
fin fonction
Clavier.class - Ecran.class - Exemple
d'exécution
|
|
![]()