Version PDF

Problématique n°1

• Comment développer de grosses applications quand on ne dispose que du "for", du "while", du "if" et du "case" pour structurer l'algorithme principal?

Solution

• Utiliser un outil de développement permettant de diviser un gros problème complexe en un ensemble de sous-problèmes
   - plus petits,
   - individuellement moins complexes,
   - aussi indépendants les uns des autres que possible
• Résoudre ces sous-problèmes
• Assembler les solutions

Exemple

• Concevoir une voiture est un problème d'une grande complexité.
• Décomposition en un ensemble de problèmes consistant à concevoir:
  • Une carrosserie
  • Un habitacle
  • Un moteur
  • Une transmission
  • Une direction
  • Un système de freinage
  • Un système d'éclairage
  • ...

Avantages

• Méthode de conception constituant en tant que telle une méthode d'analyse
• Conception globale simplifiée
• Solution de chaque problème élémentaire validable individuellement
• Validation globale simplifiée si certitude de la validation de chaque solution élémentaire
• Résolution indépendante possible de chaque problème élémentaire:
  • Travail simultané de plusieurs développeurs -> Développement accéléré
  • Affectation des problèmes à des spécialistes du domaine -> Meilleurs développements

Inconvénients

• L'ensemble des solutions élémentaires concourt à la résolution du problème global
  -> Solutions élémentaires non totalement indépendantes les unes des autres
  -> Conception de l'interaction entre les solutions élémentaires: Problème en soi
• Décomposition en sous-problèmes pas toujours possible

Problématique n°2

• Comment éviter de résoudre plusieurs fois un même problème quand celui-ci apparait plusieurs fois dans la même application ou dans des applications différentes?
• Comment faciliter la réutilisation de codes informatiques que l'on a développés?
• Comment faciliter l'utilisation de codes informatiques par d'autres personnes que celles qui les ont conçus?

• Utiliser une technique de développement permettant d'"englober" la résolution algorithmique d'un problème de manière qu'il soit possible de faire appel à l'algorithme sans le réécrire
    - Eventuellement sans même avoir accès au code source de l'algorithme
    - Eventuellement sans même connaître de façon précise comment fonctionne l'algorithme

Exemples

• En langage Java:
  • Math.sin(x) -> Calcul de sinus(x) et "retour" du résultat de ce calcul
  • "Fonction" standard du langage Java

• En langage Java:
  • Clavier.saisirInt() -> Lecture au clavier d'une valeur de type java int et "retour" du résultat de cette opération de lecture
  • "Fonction" non standard de Java (développée ad hoc pour les séances de TP -> Utilisation du fichier Clavier.class)

Avantages

• Technique algorithmique guidant l'analyse
• Réutilisation d'algorithmes développés et validés par soi-même ou par d'autres developpeurs
• Conception de vastes bibliothèques d'algorithmes (librairies, API (Application Programming Interface))
  • Exemples: Ecran.class, Clavier.class, l'API Java
• Correction des bugs plus facile
  • Trouver l'algorithme où est présent le bug
  • Le corriger dans cet algorithme
  • Correction automatiquement déployée partout où l'algorithme est utilisé

Inconvénients

• Aucun

Programmation modulaire à base de sous-algorithmes

• Sous-algorithme: Algorithme informatique développé dans le but d'être "utilisé dans" (appelé depuis) d'autres algorithmes

• Diverses dénominations pour désigner le concept de "sous-algorithme" suivant divers contextes de développement:
  • Fonction (terme usuel):
    • Programmation structurée (C, Pascal, Basic, Fortran, ADA, Java, Javascript, PHP, ...)
    • Programmation fonctionnelle (Lisp, Caml, ...)
    • Algorithmique PDL
  • Procédure:
    • Programmation structurée (Pascal, ...)
  • Méthode:
    • Programmation orientée objet (Java, C++, C#, ...)
  • Sous-programme:
    • Programmation structurée 
  • Sous-algorithme:
    • Algorithmique PDL
  • Action:
    • Algorithmique PDL

Exemple n°1: Calcul de la valeur d'un polynôme

• Problème: Ecrire un algorithme de calcul de f(x,m,n) = x^m+xⁿ où x est réel (différent de 0.0) et m et n sont des entiers positifs ou nuls. x, m et n sont acquis au clavier. Le résultat du calcul est affiché à l'écran.

Sous-algorithme

• Conçu pour réaliser un traitement
  • Bien défini
  • Bien délimité
  • Si possible de manière parfaitement indépendante au contexte particulier de l’algorithme appelant pour qu'il puisse être utilisé dans n'importe quel contexte

• Généralement muni de paramètres "passés" en entête
  • 0, 1 ou plusieurs paramètres correspondant aux "données" du traitement réalisé par le sous-algorithme
    -> Paramêtre(s) transmis en "entrée" par copie de l'algorithme appelant vers le sous-algorithme appelé
  • 0, 1 ou plusieurs paramètres correspondant aux "résultats" du traitement réalisé par le sous-algorithme
    -> Paramètre(s) transmis en "sortie" par copie du sous-algorithme appelé vers l'algorithme appelant
    
    Problèmes résolus par ce biais:
      - Communication des données de l'algorithme appelant à destination du sous-algorithme appelé
      - Communication des résultats du sous-algorithme appelé à destination de l'algorithme appelant

• Optionnellement muni de variables locales
  • Utilisation possible de variables temporaires locales au sous-algorithme (non définies en dehors) pour en assurer le traitement

• Comment déterminer les paramètres d'entrée et de sortie?
  Analyser l'énoncé du problème car celui-ci est généralement précis sur cette question
  En cas d'imprécision, responsabilité du choix laissée à la personne qui réalise l'analyse

Syntaxe en langage algorithmique

• Un entête (extrêmement important car il définit comment le sous-algorithme pourra être appelé par l'algorithme appelant):
  • Le nom du sous-algorithme (par l'intermédiaire duquel il sera désigné lors d'un appel)
  • La liste des paramètres "formels" transmis avec indication de leurs noms, types et modificateurs (paramètre en entrée, en sortie ou en entrée/sortie) tels qu'ils sont connus dans le corps du sous-algorithme

• Une zone de définition pour d'éventuelles variables locales

• Un corps de réalisation de tous les traitements de calcul des paramètres en sortie à partir des paramètres en entrée (en utilisant les variables locales à titre de variables intermédiaires de traitement)

• Syntaxe:

• Liste exhaustive des noms des paramètres
  • Le séparateur est la virgule.
  • Utilisation de la syntaxe type nomParametre pour chacun d'eux
  • Utilisation du signe -> placé avant type nomParametre pour indiquer un paramètre en entrée
  • Utilisation du signe -> placé après type nomParametre pour indiquer un paramètre en sortie

• Zone de définition des variables locales de traitement
  • Déclaration de toutes les variables locales au sous-algorithme
  • Utilisation de la syntaxe type nomVariable pour chacun d'elles

Appel à un sous-algorithme

• Appel à un sous-algorithme au moyen d'une instruction formatée sous la forme:
  nom_action(liste de parametres)
  où les paramètres "effectifs" de la liste d'appel sont donnés dans le bon ordre (celui des paramètres formels).
  Lors de l'exécution:
    - Copie des paramètres effectif vers les paramètres formels correspondant de l'entête du sous-algorithme passés en entrée
      -> Les paramètres d'appel peuvent être des variables, des constantes, des constantes littérales, des expressions, ... (i.e. toute "chose" pouvant être évaluée pour obtenir la valeur qui sera transmise par copie)
    - Exécution du corps du sous-algorithme au moyen des paramètres formels en entrée et des variables locales dans le but d'affecter les paramètres formels en sortie avec les valeurs nécessaires
    - Copie des paramètres formels du sous-algorithme passés en sortie vers les paramètres effectifs correspondants.
      -> Obligation pour ces paramètres d'appel d'être des variables car l'opération d'affectation doit être possible.

Nom des sous-algorithmes

• Lettres non accentuées, chiffres et _ autorisés
• Interdiction de débuter par un chiffre
• Conventions
  • Ecriture en minuscule
  • Si nom composé, à l'exception de la première, initiale de chaque item en majuscule
• Recommandation: Nom choisi de manière explicite vis à vis du traitement réalisé
• Exemples: testEgalite, saisirEntier
• Même nom possible pour deux sous-algorithmes si les listes de types extraites de leurs listes de paramètres d'entête sont différentes.

Exemple

• Réalisation de l'analyse visant à déterminer les données, les résultats et les traitements à réaliser pour implanter le problèmeliser pour implanter le problème
Les données sont les paramètres formels en entrée. Elles sont passées en entête et n'ont donc pas à être acquises dans le sous-algorithme.
• Les résultats sont les paramètres formels en sortie. Ils sont passés en entête et n'ont donc pas à être exploités dans le sous algorithme.
• Les traitements constituent le corps.raitements constituent le corps.

Cas particulier: Sous-algorithme sans entrée et/ou sans sortie

• Exemple: Ecran.afficher(a,b), deux entrèes, pas de sortie
• Exemple: Ecran.sautDeLigne(), ni entrée, ni sortie

• Possiblement aucun paramètre d'entête en entrée
• Possiblement aucun paramètre d'entête en sortie

Cas particulier: Sous-algorithme avec acquisition interne des données et/ou exploitation interne des résultats

• Si l'énoncé du problème le justifie: Acquisition des données du traitement (définies au moment de l'analyse) directement au sein du sous-algorithme (clavier, fichier, réseau, ...) et non en entrée en entête

• Si l'énoncé du problème le justifie: Exploitation des résultats du traitement (définis au moment de l'analyse) directement au sein du sous-algorithme (affichage à l'écran, écriture dans un fichier, ...) sans transmission en sortie en entête

• Conséquences:
   - Possiblement aucun paramètre d'entête en entrée
   - Possiblement aucun paramètre d'entête en sortie

Exemples n°2

• Enoncé (1)
  • Ecrire un sous-algorithme qui réalise les traitements suivants:
    • Lecture au clavier d'un paramètre de type réel
    • Calcul du carré de ce paramètre
    • Affichage de la valeur obtenue
  • Mini-analyse:
    Une seule donnée de traitement acquise au clavier au sein du sous-algorithme donc non passée en entrée en entête
    Un seul résultat de traitement directement affiché et donc non passé en sortie en entête de sous-algorithme

• Enoncé (2)
  • Ecrire un sous-algorithme de calcul du carré d'un réel
  • Mini-analyse:
    Une seule donnée de traitement acquise en entrée en entête
    Un seul résultat de traitement passé en sortie en entête de sous-algorithme

Implantation de l'énoncé 1 de exemple n°2

Implantation de l'énoncé 2 de exemple n°2

A l'avenir, utilisation du mot réservé "fonction" pour les sous-algorithmes à valeur retournée, utilisation du mot réservé "action" pour les sous-algorithmes sans valeur retournéelgorithmes sans valeur retournée

type fonction nom_fonction(liste exhaustive des triplets (noms,type,modificateur) des parametres formels)   déclarations de variables dont une variable v (*) retournée en fin d'action   corps du sous-algorithmep;  dont affectation de v avec la valeur à retourner   retourner v fin fonction"couleurMotReserve">fin fonction

(*) Nom de variable choisi arbitrairement

Type de donnée indiqué avant le mot réservé fonction: Type de la valeur "retournée" (rendue, renvoyée) par la fonction
• Présence dans la fonction parmi les variables locales d'une variable spécifique dédiée du type retournéécifique dédiée du type retourné
• Affectation obligatoire de cette variable avec la valeur que l'on souhaite retourner
• Utilisation de l'instruction retourner juste avant le

• Exemple d'appel à ce sous-algorithme: Affectation du résultat d'exécution à une variable
  variable <- nom_fonction(parametres effectifs)
  où les paramètres d'appel sont séparés par des virgules et apparaissent dans l'ordre de définitiont dans l'ordre de définition
Appel direct autorisé au sein d'une expression:
Ecran.afficherln(nom_fonction(parametres effectifs))

Implantation alternative de l'énoncé 2 de exemple n°2de l'énoncé 2 de exemple n°2

Implantation de l'exemple n°1

Seconde implantation de l'exemple n°1

Passages de paramètres de type agrégé en entrée, en sortie et en retour

• Utilisation de paramètres de types agrégés en entrée, en sortie et en retour autorisée en langage algorithmique
• Support de tous les types de passages en paramètre:
  • En entrée
  • En sortie
  • En entrée/sortie
  • En retour

Exemple: Sous-algorithme de calcul de l'intersection de deux droites du plan

• Développement d'un type agrégé coordonnées2D
• Deux paramètres en entrée pour passer les deux droites
• Possibilité de développer deux variantes de sous-algorithme:
    - Une fonction avec une valeur de type coordonnées2D retournée
    - Une action avec un paramètre d'entête en sortie de type coordonnées2D

• Si implantation d'une fonction, obtention d'un retour de type agrégé qui peut être utilisé pour affectation à une variable (affectation champ pour champ au moyen de l'opérateur <-), inclusion dans une expression, passage à une fonction, ...

Implantation de sous-algorithmes en langage Java

• Dénomination: "fonction" en programmation classique, "méthode" en programmation orientée objet

• Application Java:
  • Obligatoirement une fonction main d'entête "public static void main(Strings [] args)"
  • Fonction main implicitement exécutée au lancement de l'application
  • Présence possible d'autres fonctions que la fonction main:
    • Fonctions incluses dans la classe application au dessus ou en dessous de la fonction main (pas à l'intérieur)

Entête d'une fonction Java

• Nom de type juste après le mot réservé static: Type de l'unique valeur retournée par la fonction
• Utilisation du type "void" (vide en anglais) si pas de valeur retournée
  Emploi de void comme type de valeur retournée obligatoire pour de telles fonctions
  Fonctions nommées "fonction void"

Corps d'une fonction Java

• Une zone de déclaration de variables locales
• Une zone de réalisation des traitements

Appel à une fonction Java

• Syntaxe identique à la syntaxe algorithmique:
    - Le nom de la fonction suivi, entre parenthèses, de la liste des paramètres sur lesquel l'appel est réalisé
    - Si fonction non void, obtention d'un retour qui peut être utilisé pour affectation à une variable, inclusion dans une expression, passage à une fonction, ...

Implantation Java de l'exemple n°1

public class Polynome { /* Calcul de la puissance entiere d'un reel    */   static double puissance(double v,int n) {     double p;     int i;     if ( n == 0 ) {       p = 1.0; }       else {       p = v;       for ( i = 1 ; i <= n-1 ; i = i+1 ) {         p = p*v; } }     return p;   } /* Calcul d'un polynome                        */   static double polynome(double x,int m,int n) {     double res;     res = puissance(x,m)+puissance(x,n);     return res;   } /* Programme principal                         */   public static void main(String [] args) {     double x;     int m;     int n;     double p;     Ecran.afficher("SVP, x : ");     x = Clavier.saisirDouble();       Ecran.afficher("SVP, m : ");     m = Clavier.saisirInt();       Ecran.afficher("SVP, n : ");     n = Clavier.saisirInt();       p = polynome(x,m,n);     Ecran.afficherln("Resultat = ",p);   } }

Polynome.java - Exemple d'exécution

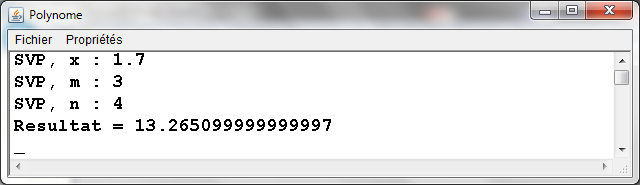Autres exemples

• Exemple 1
  • Une fonction surfaceCercle de calcul de la surface d'un cercle connu par son rayon (un réel en entrée en entête: le rayon, un réel retourné: la surface)
  • Une fonction main qui utilise la fonction surfaceCercle pour calculer et afficher la surface d'un cercle dont le rayon a été préalablement lu au clavier

public class SurfaceCercle { /* Calcul de la surface d'un cercle            */ /* Le rayon r est donne                        */   static double surfaceCercle(double r) {     double s;     s = Math.PI*r*r;     return s;   } /* Programme principal                         */   public static void main(String [] args) {     double rayon;     double surface;     Ecran.afficher("SVP, rayon : ");     rayon = Clavier.saisirDouble();       surface = surfaceCercle(rayon);     Ecran.afficherln("Surface = ",surface);   } }

SurfaceCercle.java - Exemple d'exécution

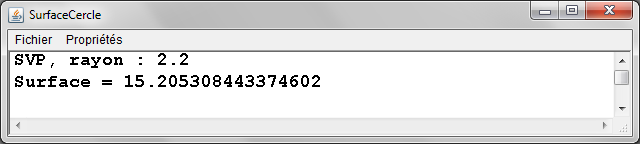• Exemple 2
  • Une fonction lectureEntierPositif de lecture au clavier d'un entier positif (essais successifs) (pas de paramètre d'entête, un entier retourné: la valeur lue)
  • Une fonction main qui utilise la fonction lectureEntierPositif pour lire au clavier et afficher un entier (simple validation du fonctionnement)

public class LectureEntierPositif { /* Lecture au clavier et retour d'un entier    */ /* Saisie par essais successifs                */   static int lectureEntierPositif() {     int v;     v = Clavier.saisirInt();     while ( v < 0 ) {       Ecran.afficher("Erreur, resaisissez : ");       v = Clavier.saisirInt(); }     return v;   } /* Programme principal                         */   public static void main(String [] args) {     int n;     Ecran.afficher("SVP, n : ");     n = lectureEntierPositif();       Ecran.afficherln("Valeur lue = ",n);   } }

LectureEntierPositif.java - Exemple d'exécution

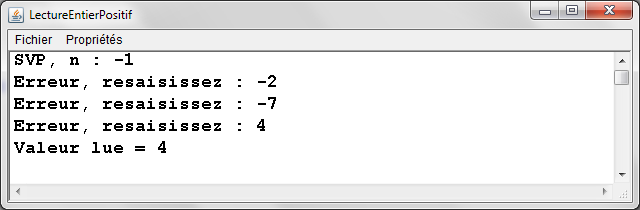• Exemple 3
  • Une fonction afficherEntiersPairs d'affichage de tous les entiers pairs entre 0 et une valeur limite (un entier en entrée en entête: la valeur limite, pas de valeur retournée),
  • Une fonction main de validation

public class AffichageEntiersPairs { /* Affichage de tous les entiers pairs entre 0 et n */   static void afficherEntiersPairs(int n) {     int i;     for ( i = 0 ; i <= n ; i = i+2 ) {       Ecran.afficher(i," "); }   } /* Programme principal                         */   public static void main(String [] args) {     int n;     Ecran.afficher("SVP, n : ");     n = Clavier.saisirInt();       afficherEntiersPairs(n);     Ecran.afficherln();   } }

AffichageEntiersPairs.java - Exemple d'exécution

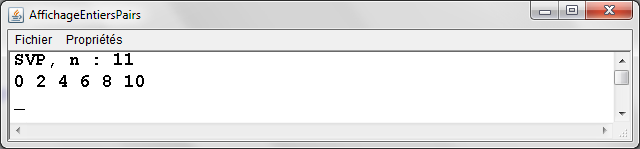Paramètres de type agrégé en entête de fonction Java?

• Comme pour les type prédéfinis, autorisation de passer des paramètres de type agrégé en entête de fonction

Exemple: Calcul du produit scalaire et calcul du produit vectoriel de deux directions 3D:

/* Type agrege de stockage d'une direction     */ /* dans un espace trois dimensions             */ /* a coordonnees reelles                       */ static class Direction3D {   double x = 0.0;   double y = 0.0;   double z = 0.0; }; /* Calcul du produit scalaire de 2 Direction3D */ static double produitScalaire(Direction3D d1,                               Direction3D d2) {   double res = d1.x*d2.x+d1.y*d2.y+d1.z*d2.z;   return res; } /* Calcul du produit vectoriel                 */ /* de 2 Direction3D                            */ static Direction3D produitVectoriel(Direction3D d1,                                     Direction3D d2) {   Direction3D res = new Direction3D();   res.x = d1.y*d2.z-d1.z*d2.y;   res.y = d1.z*d2.x-d1.x*d2.z;   res.z = d1.x*d2.y-d1.y*d2.x;   return res; } /* Programme principal                         */ public static void main(String [] args) {   Direction3D d1 = new Direction3D();   Direction3D d2 = new Direction3D();   double ps;   Direction3D pv;   Ecran.afficherln("Veuillez saisir la premiere direction");   d1.x = Clavier.saisirDouble();   d1.y = Clavier.saisirDouble();   d1.z = Clavier.saisirDouble();   Ecran.afficherln("Veuillez saisir la seconde direction");   d2.x = Clavier.saisirDouble();   d2.y = Clavier.saisirDouble();   d2.z = Clavier.saisirDouble();   ps = produitScalaire(d1,d2);   pv = produitVectoriel(d1,d2);   Ecran.afficherln("Produit scalaire : ",ps);   Ecran.afficherln("Produit vectoriel : ",pv.x,", ",pv.y,", ",pv.z); }

Produits3D.java - Exemple d'exécution

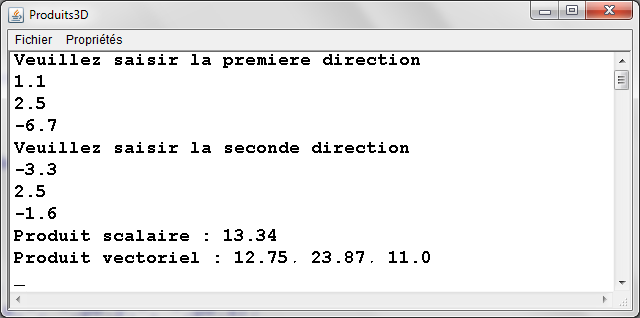Cas particulier: Retour d'un paramètre de type agrégé par une fonction non void

• Obtention d'un retour qui peut être utilisé pour affectation à une variable, inclusion dans une expression, passage à une fonction, ...
• En cas d'affectation, utilisation sans problème de l'opérateur =
  -> Disparition de l'ancienne variable agrégée (à gauche du =) remplacée par le paramètre retourné par la fonction
  -> Pas nécessaire de faire un new dans le programme appelant car il est fait dans la fonction sur la variable retournée en fin de fonction 

Passages de paramètres en entrée et en sortie en langage Javaa

• Quid des modes de passage de paramètre en entrée, en sortie et en entrée/sortie tels que définis en langage algorithmique?
• Fonctionnalité non implantée explicitement en langage Java
• Mode de passage défini implicitement par le type de paramètre

• En langage Java, mode de passage de paramètre pour les types byte, short, int, long, float, double, char, boolean et String (tous les types prédéfinis) implicitement et obligatoirement en entrée
• En langage Java, mode de passage de paramètre pour les types agrégés implicitement et obligatoirement en entrée/sortie
• En langage Java, pas de mode de passage de paramètre exclusivement en sortie

• Tous les types (prédéfini ou agrégé) supportent le mode de passage de paramètre en entrée
   -> Pas de problème pour la traduction langage algorithmique -> Java des passages de paramètre en entrée
• Seuls les types agrégés supportent le mode de passage de paramètre en sortie
   -> Problème pour la traduction langage algorithmique -> Java des passages en sortie des paramètres de type prédéfini

• Designs de programmation suivant le nombre de paramètres en sortie de type prédéfini:
  • Si 0 paramètre en sortie:
    • Une seule possibilité, une fonction void
  • Si 1 paramètre en sortie de type prédéfini A:
    • Une seule possibilité, une fonction non void avec retour d'un paramètre du type A
  • Si 2 ou plus paramètres en sortie de types prédéfinis:
    • Construction d'un type agrégé B permettant l'agrégation des paramètres en sortie en un seul paramètre agrégé
    • Deux possibilités:
      • Une fonction non void avec retour d'un paramètre de type B
      • Une fonction void avec un paramètre d'entête de type B (implicitement en entrée/sortie)

Exemple

• Développer un sous-algorithme ayant pour but de calculer un unique résultat: les coordonnées d'un point dans un espace à deux dimensions réelles
  (les données et le traitement ne sont pas ici précisés)
• En langage algorithmique, 3 possibilités:
  • Développement d'une action avec utilisation de deux paramètres d'entête de type réel nommés x et y passés en sortie
  • Création d'un type agrégeant deux champs de type réel nommés x et y
    Développement d'une action avec passage d'un paramètre d'entête de ce type passé en sortie
  • Création d'un type agrégeant deux champs de type réel nommés x et y
    Développement d'une fonction avec retour d'une valeur de ce type
• En langage Java, 2 possibilités:
  • Création d'un type agrégeant deux champs de type réel nommés x et y
    Développement d'une fonction void avec passage d'un paramètre d'entête de ce type (implicitement en entrée/sortie)
  • Création d'un type agrégeant deux champs de type réel nommés x et y
    Développement d'une fonction non void retournant comme résultat une valeur définie selon ce type

Application Java de calcul de l'intersection de deux droites du plan:

public class IntersectionDroites2D { /* Type agrege de stockage de coordonnees      */ /* reelles en deux dimensions                  */   static class Coordonnees2D {     double x = 0.0;     double y = 0.0; }; /* Type agrege de stockage des composantes     */ /* reelles d'une droite du plan                */   static class Droite2D {     double a = 0.0;     double b = 0.0; }; /* Calcul de l'intersection entre deux droites */ /* d'équations y = a1*x+b1 et y = a2*x+b2      */   static Coordonnees2D intersection(Droite2D d1,                                     Droite2D d2) {     Coordonnees2D inter = new Coordonnees2D();     inter.x = (d2.b-d1.b)/(d1.a-d2.a);     inter.y = d1.a*inter.x+d1.b;     return inter;   } /* Programme principal                         */   public static void main(String [] args) {     Droite2D d1 = new Droite2D();     Droite2D d2 = new Droite2D();     Coordonnees2D inter;     Ecran.afficher("SVP, coefficient directeur droite 1 : ");     d1.a = Clavier.saisirDouble();       Ecran.afficher("SVP, ordonnée à l'origine droite 1  : ");     d1.b = Clavier.saisirDouble();       Ecran.afficher("SVP, coefficient directeur droite 2 : ");     d2.a = Clavier.saisirDouble();       Ecran.afficher("SVP, ordonnée à l'origine droite 2  : ");     d2.b = Clavier.saisirDouble();       inter = intersection(d1,d2);     Ecran.afficherln("Intersection : ( ",inter.x," , ",inter.y," )");   } }

IntersectionDroites2D.java - Exemple d'exécution

Recommandation

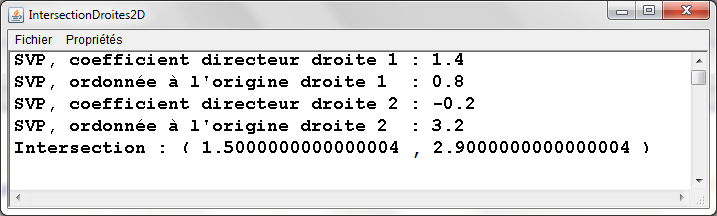• Ecrire des sous-algorithmes courts (i.e. qui tiennent entièrement à l&-> Plus lisible
• Privilégier les sous-algorithmes avec résultat retourné (fonctions)
  -> Plus clair -> Plus clair
• Structurer les informations utilisées en passage de paramètre et en retour de sous-algorithme
  -> Plus clair et plus lisible