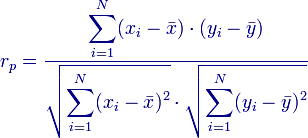|
Exercice n°1: Tableaux "simples"
a) On considère l'existence d'un tableau de réels. Ecrire un algorithme permettant de parcourir ce tableau pour afficher les valeurs qu'il
contient qui sont comprises entre une borne réelle minimale et une borne réelle maximale (bornes incluses).
|
AffichageTableauSeuils.java
public class AffichageTableauSeuils {
/* Programme principal */
public static void main(String [] args) {
/* Taille du tableau */
final int TAILLE = 20;
/* Déclaration du tableau */
double [] tab = new double[TAILLE];
int i;
double min;
double max;
/* Acquisition clavier de min et de max */
Ecran.afficher("SVP, valeur minimale? ");
min = Clavier.saisirDouble();
Ecran.afficher("SVP, valeur maximale? ");
max = Clavier.saisirDouble();
/* Remplissage du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
tab[i] = Math.random(); }
/* Affichage des valeurs du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
Ecran.afficherln(tab[i]); }
Ecran.sautDeLigne();
/* Affichage des valeurs du tableau */
/* incluses dans l'intervalle [min,max] */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
if ( ( tab[i] >= min ) && ( tab[i] <= max ) ) {
Ecran.afficherln(tab[i]); } }
}
}
Clavier.class - Ecran.class - Exemple d'exécution
|
b) On considère l'existence d'un tableau de réels. Ecrire un algorithme permettant de calculer et d'afficher la moyenne des valeurs contenues
dans ce tableau.
|
MoyenneTableau.java
/* Calcul de la moyenne des valeurs contenues */
/* dans un tableau de reels double */
public class MoyenneTableau {
/* Programme principal */
public static void main(String [] args) {
/* Taille du tableau */
final int TAILLE = 20;
/* Déclaration du tableau */
double [] tab = new double[TAILLE];
int i;
double moyenne;
double somme;
/* Remplissage du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
tab[i] = Math.random(); }
/* Affichage des valeurs du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
Ecran.afficherln(tab[i]); }
Ecran.sautDeLigne();
/* Calcul puis affichage de la moyenne */
/* des valeurs du tableau */
somme = 0.0;
for ( i = 0 ; i < tab.length ; i = i+1 ) {
somme = somme+tab[i]; }
moyenne = somme/tab.length;
Ecran.afficherln("La moyenne est ",moyenne);
}
}
Clavier.class - Ecran.class - Exemple d'exécution
|
c) On considère l'existence d'un tableau de réels. Ecrire un algorithme permettant de déterminer et d'afficher le nombre de valeurs présentes
dans ce tableau qui sont inférieures ou égales à une valeur réelle limite.
|
NombreValeursInferieuresLimite.java
/* Calcul du nombre de valeurs inferieures */
/* ou egales a une valeur limite trouvees */
/* dans un tableau de double */
public class NombreValeursInferieuresLimite {
/* Programme principal */
public static void main(String [] args) {
/* Taille du tableau */
final int TAILLE = 20;
/* Déclaration du tableau */
double [] tab = new double[TAILLE];
int i;
double limite;
int cpt;
Ecran.afficher("SVP, valeur limite? ");
limite = Clavier.saisirDouble();
/* Remplissage du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
tab[i] = Math.random(); }
/* Affichage des valeurs du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
Ecran.afficherln(tab[i]); }
Ecran.sautDeLigne();
cpt = 0;
for ( i = 0 ; i < tab.length ; i = i+1 ) {
if ( tab[i] <= limite ) {
cpt = cpt+1; } }
Ecran.afficherln("Nombre valeurs < a ",limite," : ",cpt);
}
}
Clavier.class - Ecran.class - Exemple
d'exécution
|
d) On considère l'existence d'un tableau de réels. Les valeurs qu'il contient sont comprises dans l'intervalle [0.0, 20.0[. Ecrire
un algorithme permettant de calculer et d'afficher les nombres de valeurs de ce tableau comprises dans les intervalles [0.0,1.0[, [1.0, 2.0[,
[2.0, 3.0[, ..., [19.0, 20.0[ (opération de "classification" en statistiques).
|
ClassificationTableau.java
/* Calcul des nombres de valeurs */
/* par intervalle de largeur 1.0 */
/* pour un tableau de double compris */
/* dans l'intervalle [0.0,20.0[ */
public class ClassificationTableau {
/* Programme principal */
public static void main(String [] args) {
/* Taille du tableau */
final int TAILLE = 20;
/* Déclaration du tableau */
double [] tab = new double[TAILLE];
int i;
int cl;
/* Remplissage du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
tab[i] = Math.random()*20.0; }
/* Affichage des valeurs du tableau */
for ( i = 0 ; i < tab.length ; i = i+1 ) {
Ecran.afficherln(tab[i]); }
Ecran.sautDeLigne();
/* Calcul puis affichage des nombres */
/* de valeurs par intervalle de largeur */
/* 1.0 pour le tableau de double compris */
/* dans l'intervalle [0.0,20.0[ */
int [] classification = new int[20];
for ( i = 0 ; i < classification.length ; i = i+1 ) {
classification[i] = 0; }
for ( i = 0 ; i < tab.length ; i = i+1 ) {
cl =(int) tab[i];
classification[cl] = classification[cl]+1; }
Ecran.afficherln("Nombres de valeurs:");
for ( i = 0 ; i < classification.length ; i = i+1 ) {
Ecran.afficherln(i," ",classification[i]); }
}
}
Clavier.class - Ecran.class - Exemple d'exécution
|
Exercice n°2: Tableaux en sous-algorithmes
a) Ecrire un sous-algorithme d'initialisation d'un tableau de n réels (n donné) au moyen de valeurs tirées au sort dans l'intervalle
[0.0,max[ où max est un réel donné. Ecrire un sous-algorithme de génération d'un tableau de n réels (n donné) au moyen de valeurs tirées
au sort dans l'intervalle [0.0,max[ où max est un réel donné. Ecrire un sous-algorithme d'affichage des valeurs contenues dans un tableau
de réels.
|
FonctionsGenerationTableau.java
/* Sous-algorithme d'affichage d'un tableau */
/* de double */
/* Sous-algorithmes d'initialisation */
/* et de generation d'un tableau de double */
/* tirés au sort */
/* Utilisation de ces sous-algorithmes */
public class FonctionsGenerationTableau {
/* Fonction d'affichage d'un tableau de double */
/* tab : Le tableau à afficher */
static void affichage(double [] tab) {
int i;
for ( i = 0 ; i < tab.length ; i = i+1 ) {
Ecran.afficherln(tab[i]); }
}
/* Fonction d'initialisation d'un tableau */
/* de double avec des nombres tirés au sort */
/* dans l'intervalle [0.0,max[ */
/* max : La borne supérieure de l'intervalle */
/* tab : Le tableau à initialiser */
static void initialisationRand(double [] tab,double max) {
int i;
for ( i = 0 ; i < tab.length ; i = i+1 ) {
tab[i] = Math.random()*max; }
}
/* Fonction de génération et retour */
/* d'un tableau de double avec des nombres */
/* tirés au sort dans l'intervalle [0.0,max[ */
/* n : La taille du tableau généré */
/* max : La borne supérieure de l'intervalle */
static double [] generationRand(int n,double max) {
double [] tab = new double[n];
initialisationRand(tab,max);
return tab;
}
/* Programme principal */
public static void main(String [] args) {
int n;
double limite;
double [] t;
Ecran.afficher("SVP, taille du tableau? ");
n = Clavier.saisirInt();
Ecran.afficher("SVP, valeur limite? ");
limite = Clavier.saisirDouble();
t = generationRand(n,limite);
affichage(t);
}
}
Clavier.class - Ecran.class - Exemple
d'exécution
|
b) Reprendre les questions (c) et (d) de l'exercice n°1 en les implantant avec utilisation de sous-algorithmes.
|
FonctionNombreValeursInferieuresLimite.java
/* Fonction de calcul et retour du nombre */
/* de valeurs inférieures ou égales */
/* à une valeur limite trouvées */
/* dans un tableau de double */
/* t : Le tableau de double de recherche */
/* limite : La valeur limite */
static int nbValeursInferieuresLimite(double [] t,
double limite) {
int cpt;
int i;
cpt = 0;
for ( i = 0 ; i < t.length ; i = i+1 ) {
if ( t[i] <= limite ) {
cpt = cpt+1; } }
return cpt;
}
Clavier.class - Ecran.class - Exemple
d'exécution
|
|
FonctionClassificationTableau.java
/* Fonction de calcul des nombres de de valeurs */
/* par intervalle de largeur 1.0 */
/* pour un tableau de double compris */
/* entre 0.0 et 20.0 */
/* Un tableau de 20 entiers est calculé */
/* et retourné */
/* t : Le tableau de double subissant */
/* l'opération de classification */
static int [] classification(double [] t) {
int i;
int cl;
int [] classification = new int[20];
for ( i = 0 ; i < 20 ; i = i+1 ) {
classification[i] = 0; }
for ( i = 0 ; i < t.length ; i = i+1 ) {
cl =(int) t[i];
classification[cl] = classification[cl]+1; }
return classification;
}
Clavier.class - Ecran.class - Exemple
d'exécution
|
c) Ecrire un sous-algorithme de fusion de deux tableaux d'entiers triés en un seul nouveau tableau d'entiers trié.
|
FusionTableaux.java
/* Fonction de fusion de 2 tableau d'entiers */
/* tries t1 et t2 en un nouveau tableau */
/* d'entiers trie */
/* Le tableau ainsi obtenu est retourné */
/* t1 : Le premier tableau trié */
/* t2 : Le second tableau trié */
static int [] fusion(int [] t1,int [] t2) {
int l = t1.length+t2.length;
int [] t = new int[l];
int i;
int i1;
int i2;
i1 = 0;
i2 = 0;
for ( i = 0 ; i < l ; i = i+1 ) {
if ( i1 == t1.length ) {
t[i] = t2[i2];
i2 = i2+1; }
else {
if ( i2 == t2.length ) {
t[i] = t1[i1];
i1 = i1+1; }
else {
if ( t1[i1] < t2[i2] ) {
t[i] = t1[i1];
i1 = i1+1; }
else {
t[i] = t2[i2];
i2 = i2+1; } } } }
return t;
}
Clavier.class - Ecran.class - Exemple d'exécution
|
Exercice n°3: Tableaux de variables de type agrégé
a) On considère le type agrégé sommet3D constitué des 3 champs x, y et z réels représentant les coordonnées d'une position dans un espace 3D.
Développer un sous-algorithme de calcul du barycentre d'un nuage de points stocké dans un tableau de sommets3D.
On rappelle que le barycentre d'un nuage de points est le point dont:
- la coordonnée x est la moyenne des coordonnées x des points du nuage,
- la coordonnée y est la moyenne des coordonnées y des points du nuage,
- la coordonnée z est la moyenne des coordonnées z des points du nuage.
|
BarycentreNuageSommets3D.java
/* Type agrege de stockage d'un sommet 3D */
static class Sommet3D {
double x = 0.0;
double y = 0.0;
double z = 0.0; };
/* Fonction de calcul et de retour */
/* du barycentre d'un nuage de points stocké */
/* dans un tableau de Sommet3D */
static Sommet3D barycentre(Sommet3D [] tp) {
Sommet3D p = new Sommet3D();
int i;
for ( i = 0 ; i < tp.length ; i = i+1 ) {
p.x = p.x+tp[i].x;
p.y = p.y+tp[i].y;
p.z = p.z+tp[i].z; }
p.x = p.x/tp.length;
p.y = p.y/tp.length;
p.z = p.z/tp.length;
return p;
}
Clavier.class - Ecran.class - Exemple d'exécution
|
b) On considère le type agrégé sommet2D constitué des 2 champs x et y réels représentant l'abscisse et l'ordonnée d'une position du plan.
1) Développer un sous-algorithme de création d'un tableau de sommet2D initialisé avec les positions des sommets d'un polygone régulier
respectant les propriétés suivantes:
- Son rayon est r.
- Il possède n sommets.
- Il est centré sur l'origine.
- L'un de ses sommets est en position (r,O.O).
2) Développer un sous-algorithme de calcul de la longueur d'une ligne polygonale non fermée stockée dans un tableau de sommet2D.
3) Développer un sous-algorithme de calcul de la longueur d'une boucle polygonale (fermée) stockée dans un tableau de sommet2D.
Les positions des n sommets d'un polygone régulier respectant les propriétés demandées peuvent être obtenues en calculant les n couples de valeurs
(r*cos(alpha),r*sin(alpha)) avec alpha = i*2.0*PI/n et i variant de 0 à n-1.
On rappelle que la distance d existant entre deux positions du plan (x1,y1) et (x2,y2) peut être calculée en utilisant la formule d = sqrt((x2-x1)2+(y2-y1)2)
|
TableauSommets2D.java
/* Type agrege de stockage d'un sommet 2D */
static class Sommet2D {
double x = 0.0;
double y = 0.0; };
/* Fonction de creation et de retour */
/* d'un tableau de Sommet2D initialise */
/* avec les positions des sommets */
/* d'un polygone regulier */
/* centre sur l'origine et de rayon r */
/* n : Le nombre de sommets du polygone */
/* r : Le rayon du polygone */
static Sommet2D [] polygoneRegulier(int n,double r) {
int i;
double angle;
Sommet2D [] t = new Sommet2D[n];
for ( i = 0 ; i < n ; i = i+1 ) {
angle = i * 2.0 * Math.PI / n;
t[i] = new Sommet2D();
t[i].x = r * Math.cos(angle);
t[i].y = r * Math.sin(angle); }
return t;
}
/* Fonction de calcul et de retour */
/* de la distance entre deux Sommet2D */
/* p1 : Le premier Sommet2D */
/* p2 : Le second Sommet2D */
static double distance(Sommet2D p1,Sommet2D p2) {
double l;
double dx;
double dy;
dx = p2.x-p1.x;
dy = p2.y-p1.y;
l = Math.sqrt(dx*dx+dy*dy);
return l;
}
/* Fonction de calcul de la longueur */
/* d'une ligne polygonale ouverte stockee */
/* dans un tableau de Sommet2D */
/* t : Le tableau de Sommet2D contenant */
/* les position des sommets de la ligne */
static double longueurLigne(Sommet2D [] t) {
double l;
l = 0.0;
int i;
for ( i = 0 ; i < t.length-1 ; i++ ) {
l = l+distance(t[i],t[i+1]); }
return l;
}
/* Fonction de calcul de la longueur */
/* d'une boucle polygonale stockee */
/* dans un tableau de Sommet2D */
/* t : Le tableau de Sommet2D contenant */
/* les position des sommets de la boucle */
static double longueurBoucle(Sommet2D [] t) {
double l;
l = longueurLigne(t) + distance(t[0],t[t.length-1]);
return l;
}
Clavier.class - Ecran.class - Exemple d'exécution
|
Exercice n°4: Type agrégé avec tableau
a) Vous êtes employé au service "contrôle qualité" d'une usine de fabrication de fraises Tagada. Vous devez concevoir un programme
informatique permettant d'analyser des échantillons de fraises pour vérifier divers critères. Parmi ceux-ci nous allons nous attacher au poids.
1) Développer un type agrégé permettant de coder un échantillon de fraises en conservant les informations suivantes: le numéro de la machine
de fabrication, la date de fabrication, 1000 poids de fraise (fraises sélectionnées aléatoirement sur la machine). On précise que numéro de machine
est un entier, la date de fabrication est une chaine de caractères (format "jj/mm/aaaa") et le poids d'une fraise est un réel comptant
en grammes.
2) Développer un sous-algorithme de calcul du pourcentage de fraises d'un échantillon qui ne respectent pas le critère consistant à avoir
un poids compris entre une valeur réelle minimale et une valeur réelle maximale.
3) Développer un sous-algorithme de détermination de la valeur médiane des 1000 poids au sens de l'ordre croissant des poids.
On rappelle que la valeur médiane d'un ensemble de valeurs selon un critère d'ordre total est une valeur v telle qu'il existe dans l'ensemble
"autant" de valeurs respectant le critère vis à vis de v que de valeurs ne le respectant pas. Pour un ensemble dont le nombre d'éléments
n est impair, on pourra prendre comme médiane la valeur du (n/2+1)eme élément de l'ensemble après tri selon le critère. Si le nombre
d'éléments est pair, on pourra prendre comme médiane la valeur moyenne des (n/2)eme et (n/2+1)eme éléments de l'ensemble
après tri selon le critère.
On pourra spécifier et considérer comme existant un sous-algorithme permettant de trier un ensemble de valeurs réelles stocké dans un tableau.
|
EchantillonFraisesTagada.java
/* Type agrege de stockage d'un echantillon */
/* de poids pour 100 fraises Tagada */
static class EchantillonFraises {
int numeroMachine = 0;
String dateEchantillon = "01/01/1901";
double [] poids = new double[1000]; };
/* Fonction de calcul et retour du pourcentage */
/* de fraises présentes dans un echantillon */
/* qui ont un poids hors d'un intervalle */
/* [minimum,maximum] */
/* ef : L'echantillonFraises analysé */
/* minimum : La borne inférieure réelle */
/* de l'intervalle de recherche */
/* maximum : La borne supérieure réelle */
/* de l'intervalle de recherche */
static double pourcentagePoidsHorsLimites(EchantillonFraises ef,
double minimum,
double maximum) {
double prctg;
int i;
int cpt;
cpt = 0;
for ( i = 0 ; i < ef.poids.length ; i = i+1 ) {
if ( ( ef.poids[i] < minimum ) || ( ef.poids[i] > maximum ) ) {
cpt = cpt+1; } }
prctg = cpt/10.0;
return prctg;
}
/* Fonction de calcul et retour de la valeur */
/* médiane du poids des fraises présentes */
/* dans un echantillon */
/* ef : L'echantillonFraises analysé */
static double medianePoids(EchantillonFraises ef) {
double [] poidsTries = ensembleTrie(ef.poids);
double mediane;
int indice;
indice = ef.poids.length/2-1;
mediane = (ef.poids[indice]+ef.poids[indice+1])/2.0;
return mediane;
}
/* Fonction de génération et retour */
/* du tableau de double contenant les mêmes */
/* valeurs qu'un tableau de double "source", */
/* mais ordonnées par ordre croissant */
/* src : Le tableau de double source */
static double [] ensembleTrie(double [] src) {
int i,j ;
double aux;
int n = src.length;
double [] dst = new double[n];
for ( i = 0 ; i < n ; i = i+1 ) {
dst[i] = src[i]; }
for ( i = 0 ; i < n-1 ; i++ ) {
for ( j = 0 ; j < n-i-1 ; j++ ) {
if ( dst[j] > dst[j+1] ) {
aux = dst[j];
dst[j] = dst[j+1];
dst[j+1] = aux; } } }
return dst;
}
Clavier.class - Ecran.class - Exemple
d'exécution
|
b) On souhaite calculer le coefficient de corrélation linéaire défini entre deux séries de N=15 données réelles.
1) Définir un type agrégé permettant de stocker ces deux séries de données en une seule variable.
2) Implanter un sous-algorithme permettant de calculer le coefficient de corrélation linéaire existant entre les deux séries de données stockées
au sein d'une variable du type agrégé de la question (1). On utilisera la formule de calcul suivante définie pour les séries x et y numérotée
de 1 à N (wikipedia):
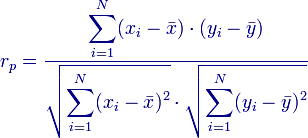
Les x et y surmontés d'une barre horizontale désignent en mathématique les moyennes des séries x et y.
|
CoefficientCorrelationLineaire.java
/* Type agrege de stockage de deux tableaux */
/* de 15 double */
static class DeuxSeries {
double [] x = new double[15];
double [] y = new double[15]; };
/* Fonction de calcul et retour */
/* de la moyenne des valeurs */
/* contenues dans un tableau de double */
/* t : Le tableau de double cible */
static double moyenne(double [] t) {
double moyenne;
int i;
moyenne = 0.0;
for ( i = 0 ; i < t.length ; i = i+1 ) {
moyenne = moyenne+t[i]; }
moyenne = moyenne/t.length;
return moyenne;
}
/* Fonction de calcul et retour */
/* de l'écart quadratique des valeurs contenues */
/* dans un tableau de double */
/* t : Le tableau de double cible */
/* m : La valeur par rapport à laquelle */
/* l'écrat quadratique est calculé */
static double ecartQuadratique(double [] t,
double m) {
double v;
int i;
v = 0.0;
for ( i = 0 ; i < t.length ; i = i+1 ) {
v = v + (t[i]-m)*(t[i]-m); }
v = Math.sqrt(v);
return v;
}
/* Fonction de calcul et retour du coefficient */
/* de correlation lineaire existant */
/* entre deux series de valeurs reelles */
/* ds : Le parametre de type DeuwSeries */
/* dans lequel les deux series de valeurs */
/* sont stockées */
static double coefficientCorrelation(DeuxSeries ds) {
double cc;
int i;
double mx;
double my;
double eqmx;
double eqmy;
mx = moyenne(ds.x);
my = moyenne(ds.y);
cc = 0.0;
for ( i = 0 ; i < ds.x.length ; i = i+1 ) {
cc = cc + (ds.x[i]-mx)*(ds.y[i]-my); }
eqmx = ecartQuadratique(ds.x,mx);
eqmy = ecartQuadratique(ds.y,my);
cc = cc / (eqmx*eqmy);
return cc;
}
Clavier.class - Ecran.class - Exemple
d'exécution
|
Exercice n°5
Un texte est stocké dans un tableau de caractères. On souhaite crypter ce texte de manière à le rendre illisible de manière directe. La méthode de
cryptage utilisée consiste à transformer chaque caractère c du texte originel par un nouveau caractère cn selon la formule cn = f(c).
La fonction f est une fonction simple qui fait correspondre de manière bijective un caractère à un autre caractère. Ce pourra être par exemple:
f('a') = 'c', f('b') = 'r', f('c') = 'z', f('d') = 'e', f(' ') = 'é',
...
a) Définir un type de données clefDeCryptage qui permettra de stocker l'ensemble des associations (caractère à coder, caractère une fois codé)
utilisées lors d'une opération de cryptage ou de décryptage.
b) Développer un sous-algorithme de cryptage d'un tableau de caractères. Si un caractère du tableau à crypter n'apparait pas dans la clef
de cryptage telle qu'elle a été conçue, il est reporté tel quel.
c) Développer un sous-algorithme de décryptage d'un tableau de caractères.
|
Cryptage.java
/* Type agrege de stockage */
/* d'une clef de cryptage */
static class ClefDeCryptage {
char [] cn = new char[256]; };
/* Fonction de cryptage d'un tableau */
/* de caracteres en un nouveau tableau */
/* de caracteres retourné */
/* t : Le tableau de caracteres à crypter */
/* cdc : La clef de cryptage à utiliser */
static char [] cryptage(char [] t,ClefDeCryptage cdc) {
int i;
char [] tc = new char[t.length];
for ( i = 0 ; i < tc.length ; i++ ) {
tc[i] = cdc.cn[t[i]]; }
return(tc);
}
/* Fonction de calcul et retour de la clef */
/* de cryptage inverse d'une clef de cryptage: */
/* la clef utilisable pour décrypter */
/* en effectuant une opération de cryptage */
/* Retour de la clef obtenue */
/* cdc : La clef de cryptage à inverser */
static ClefDeCryptage clefDeDecryptage(ClefDeCryptage cdc) {
ClefDeCryptage cddc = new ClefDeCryptage();
int i;
for ( i = 0 ; i < 256 ; i++ )
cddc.cn[cdc.cn[i]] =(char) i;
return(cddc);
}
/* Fonction de decryptage d'un tableau */
/* de caracteres en un nouveau tableau */
/* de caracteres retourné */
/* t : Le tableau de caracteres à decrypter */
/* cdc : La clef de cryptage utilisée */
/* pour le cryptage initial */
static char [] decryptage(char [] t,ClefDeCryptage cdc) {
ClefDeCryptage cddc = clefDeDecryptage(cdc);
char [] tc = new char[t.length];
int i;
for ( i = 0 ; i < tc.length ; i++ ) {
tc[i] = cddc.cn[t[i]]; }
return(tc);
}
Clavier.class - Ecran.class - Exemple d'exécution
|
Exercice n°6
On souhaite implanter une "structure de données" permettant de stocker un ensemble de chaînes de caractères pour un maximum de 20 chaînes
de caractères.
1) Définir un type agrégé permettant de stocker un tel ensemble (initialisé à l'ensemble vide).
2) Implanter un sous-algorithme permettant d'afficher les chaînes de caractères présentes dans un ensemble de chaînes de caractères.
3) Implanter un sous-algorithme permettant d'ajouter une chaîne de caractères à un ensemble de chaînes de caractères (l'ajout d'une
chaîne existant déjà est autorisé).
4) Implanter un sous-algorithme permettant de tester si une chaîne de caractères appartient à un ensemble de chaînes de caractères.
5) Implanter un sous-algorithme permettant de fusionner 2 ensembles de chaînes de caractères en un nouvel ensemble de chaînes de caractères.
6) Implanter un sous-algorithme permettant de retirer une chaîne de caractères d'un ensemble de chaînes de caractères.
7) Implanter un sous-algorithme permettant de tester si un ensemble de chaînes de caractères est vide.
|
EnsembleDeChainesDeCaracteres.java
/* Type agrege de stockage d'un ensemble */
/* d'au maximum 20 chaines de caracteres */
static class EnsembleDeChaines {
final int MAX = 20;
int n = 0;
String [] s = new String[MAX]; };
/* Fonction d'affichage des chaines */
/* de caracteres contenues dans un ensemble */
/* de chaines de caracteres */
/* edc : L'EnsembleDeChaines à afficher */
static void affichage(EnsembleDeChaines edc) {
int i;
for ( i = 0 ; i < edc.n ; i = i+1 ) {
Ecran.afficherln(edc.s[i]); }
}
/* Fonction d'ajout d'une chaine de caracteres */
/* a un ensemble de chaines de caracteres */
/* Retour de true si l'ajout a abouti */
/* Retour de false si plus de place */
/* edc : L'EnsembleDeChaines où l'ajout */
/* est effectué */
/* s : La chaine ajoutée */
static boolean ajout(EnsembleDeChaines edc,String s) {
boolean res;
if ( edc.n < edc.MAX ) {
edc.s[edc.n] = s;
edc.n = edc.n+1;
res = true; }
else {
res = false; }
return res;
}
/* Fonction de test de l'appartenance */
/* d'une chaine de caracteres a un ensemble */
/* de chaines de caracteres */
/* Retour de true si présent, false sinon */
/* edc : L'EnsembleDeChaines où la recherche */
/* est effectuée */
/* s : La chaine recherchée */
static boolean appartient(EnsembleDeChaines edc,String s) {
boolean res = false;
int i = 0;
while ( ( res == false ) && ( i < edc.n ) ) {
res = (edc.s[i] == s);
i = i+1; }
return res;
}
/* Fonction de fusion de deux ensembles */
/* de chaines de caracteres en un nouvel */
/* ensemble de chaines de caracteres */
/* Retour de true si la fusion est possible */
/* Retour de false si la fusion est impossible */
/* car pas assez de place */
/* edc1 : Le premier EnsembleDeChaines */
/* edc2 : Le second EnsembleDeChaines */
/* edc : L'EnsembleDeChaines à remplir */
static boolean fusion(EnsembleDeChaines edc1,
EnsembleDeChaines edc2,
EnsembleDeChaines edc) {
int i;
boolean res;
if ( edc1.n+edc2.n <= edc.MAX ) {
edc.n = 0;
for ( i = 0 ; i < edc1.n ; i = i+1 ) {
ajout(edc,edc1.s[i]); }
for ( i = 0 ; i < edc2.n ; i = i+1 ) {
ajout(edc,edc2.s[i]); }
res = true; }
else {
res = false; }
return res;
}
/* Fonction de retrait d'une chaine */
/* de caracteres à un ensemble de chaines */
/* de caracteres */
/* Retour de true si le retrait a abouti */
/* Retour de false sinon */
/* edc : L'EnsembleDeChaines où le retrait */
/* est réalisé */
/* s : La chaine retirée */
static boolean retrait(EnsembleDeChaines edc,String s) {
boolean res = false;
int i = 0;
while ( ( res == false ) && ( i < edc.n ) ) {
res = (edc.s[i] == s);
i = i+1; }
if ( res ) {
for ( ; i < edc.n ; i = i+1 ) {
edc.s[i-1] = edc.s[i]; }
edc.n = edc.n-1; }
return res;
}
/* Fonction de test si un ensemble de chaines */
/* de caracteres est vide */
/* Retour de true si c'est le cas, false sinon */
/* edc : L'EnsembleDeChaines testé */
static boolean estVide(EnsembleDeChaines edc) {
return (edc.n == 0);
}
Clavier.class - Ecran.class - Exemple
d'exécution
|
|
![]()
![]()