Sujets et Exercices
de TD et TP
Mini-langage
pour
la modélisation
OpenGL, fonctions basiques pour la modélisation
Auxiliary library d'OpenGL
Programmation au moyen de fonctions C
Animations
Caméras, implantation en VRML et en OpenGL
Mise en route en VRML et en OpenGL
Utilisation des primitives graphiques
Dernière modification
16/11/09 07:03:33
On se donne le mini-langage de description de scènes composé des instructions suivantes:
C pour le dessin d'un cube de coté 1, centré sur l'origine,
S pour le dessin d'une sphère de rayon 1, centré sur l'origine,
Cy pour le dessin d'un cylindre d'axe y, de hauteur 1, de rayon 1, centré sur l'origine,
Co pour le dessin d'un cône d'axe y, de hauteur 1, de rayon 1, centré sur l'origine,
T(x,y,z) pour réaliser une translation de vecteur (x,y,z),
R(a,x,y,z) pour réaliser une rotation d'angle a autour de l'axe de vecteur directeur (x,y,z) passant par l'origine,
Z(rx,ry,rz) pour réaliser un zoom de rapports rx, ry et rz selon les axes x, y et z.
Programmer les scènes suivantes:
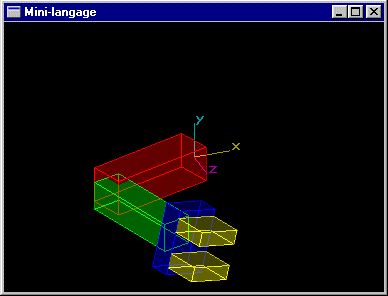
Scène (1): Quatre cubes de coté 1.0 aux positions (1.5,0.0,1.5), (1.5,0.0,-1.5), (-1.5,0.0,1.5), (-1.5,0.0,-1.5).
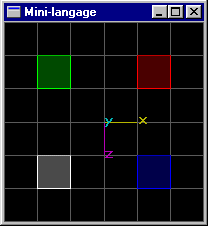
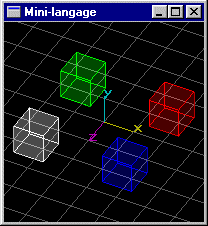
Scène (2): Même scène que précédemment, mais le cube de position (1.5,0.0,1.5) subit une rotation de 45° autour de l'axe y passant par son centre.
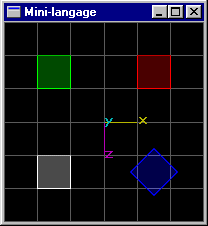
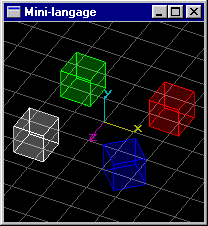
Scène (3): Même scène que précédemment, mais le cube de position (-1.5,0.0,1.5) possède une dimension en z égale à 2.
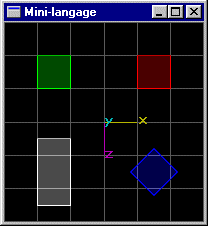
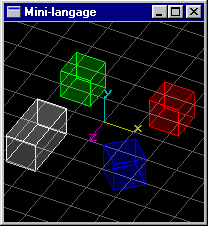
Scène (4): Même scène que précédemment, mais le cube de position (-1.5,0.0,-1.5) subit une rotation de 40° autour de l'axe y passant par son centre et une dimension en z égale à 2.
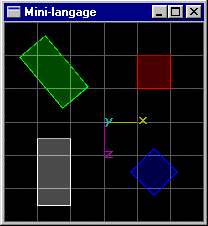
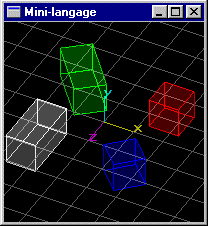
Scène (5): Même scène que la scène (3), mais le cube de position (-1.5,0.0,-1.5) subit une rotation de 30° autour de l'axe y passant par le centre de sa base de z maximum.
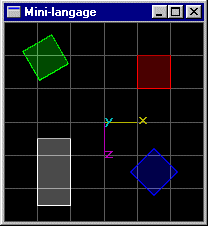
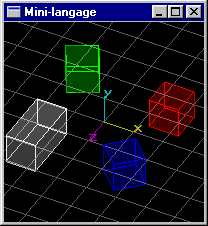
On se donne les instructions mini-langage supplémentaires suivantes:
Push pour l'empilement du repère courant
Pop pour le dépilement vers le repère courant du repère situé en haut de la pile de repères
Réécrire la scène (5) en exploitant ces deux nouvelles instructions et en rendant les objets indépendants les uns des autres.
Programmer la scène (6) suivante:
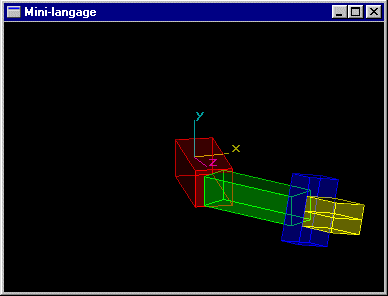
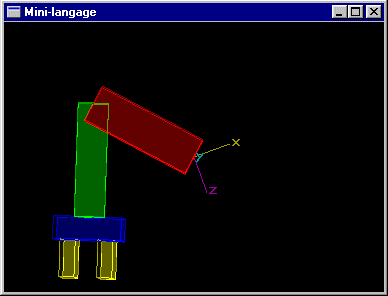
Un bras robot composé d'un avant-bras, d'un bras, et d'une paire de pinces. L'avant-bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un parallélépipède rectangle de dimension (3,1,1) (rouge). Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède rectangle de dimension (3,0.8,0.8) (vert). La pince est située au bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. Le montant de la paire de pinces est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (bleu). Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4) (jaune) à même de se déplacer longitudinalement d'une valeur d pour réaliser une ouverture totale de 2xd.
Solutions OpenGL
Aux |
GLUt |
|||
| Les cubes | ||||
| Le bras robot | ||||
| Le temple | ||||
Reprendre les scènes du TD précédent et les programmer en VRML.
Solutions
| Solution scène (1) |
| Solution scène (2) |
| Solution scène (3) |
| Solution scène (4) |
| Solution scène (5) |
| Solution scène (5bis) |
| Solution scène (6) r1 = p/4, r2 = p/6, r3 = p/3, d = 0.2 |
Reprendre les scènes du TD précédent et les programmer en VRML.
On s'efforcera d'écrire des fonctions C destinées à être utilisées au sein de fonctions display.
Définir un type coordonnées dans un espace à trois dimensions.
Définir un type couleur.
Définir un type source lumineuse ponctuelle.
Définir un type matériau de surface.
Spécifier et écrire une fonction C calculant l'énergie lumineuse reçue en un point arbitraire depuis une source lumineuse ponctuelle.
Spécifier et écrire une fonction C évaluant l'énergie lumineuse diffusée (formule de Lambert) en un point d'une surface éclairé par une source lumineuse ponctuelle.
Soit une sphère S de rayon 1 centrée sur l'origine. Soit un rayon R défini par son équation paramétrique.
Ecrire une fonction permettant de tester l'existence d'une intersection entre S et R.
Ecrire une fonction calculant les caractéristiques du rayon obtenu par réflexion du rayon R sur la sphère S.
Définir un type coordonnées en 3D.
Définir un type polygone dans R3.
Spécifier et écrire une fonction C permettant le calcul de n points modélisant la courbe de Bézier générée à partir d'un polygone de R3.
On se donne les 5 points de contrôle (3,2,-1), (-4,5,-4), (-5,4,3), (-1,-3,-2) et (4,-1,0). Ecrire une fonction display assurant la génération et le dessin de 100 points modélisant la courbe de Bézier associée à ces cinq points.
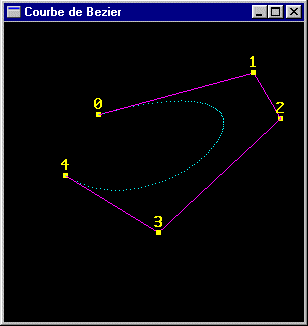
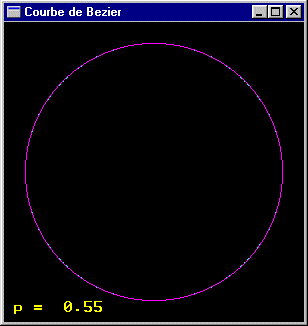
On souhaite modéliser un "cercle" du plan xOz au moyen de morceaux de courbes de Bézier. Décrire une méthode permettant de générer ce cercle. Programmer cette méthode.
Bézier en GL: Forme par extrusion
On souhaite modéliser un "tuyau" de l'espace (section circulaire) au moyen de morceaux de surfaces de Bézier. Décrire une méthode permettant de générer ce cylindre. Programmer cette méthode.
Bézier en GL: Forme par révolution
On souhaite modéliser un "vase" de l'espace au moyen de morceaux de surfaces de Bézier. Décrire une méthode permettant de générer ce vase. Programmer cette méthode.

Utiliser les NURBS de GLU pour programmer la génération d'une surface NURBS modélisant de la tôle ondulée.
![]()
Le but du TP est de programmer deux fonctions de dessin de cylindre et de dessin de cône. Ces deux fonctions devront autoriser les paramétrages suivants:
choix des surfaces affichées:
bord, base inférieure et/ou base supérieure pour le cylindre,
bord et/ou base inférieure pour le cône,
choix du nombre de segments de facettisation,
choix de la hauteur,
choix du rayon.
De manière à supporter la gestion d'un éclairage, ces fonctions devront gérer, outre la position des sommets de facettisation, la création de normales extérieures au niveau de ces sommets.


Solution
Le but du TP est de programmer une fonction de clipping permettant de restreindre le tracé d'un segment à une portion parallélipipédique de l'espace par généralisation de l'algorithme de Cohen-Sutherland de R2 vers R3.
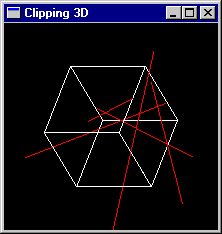
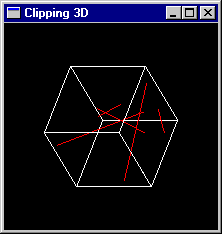
Solution
Aux |
GLUt |
|||
| Clipping de Cohen-Sutherland en 3D | ||||