Le processus
de visualisation
PROJECTIONS
PLANAIRES
Définition
Propriétés
OPÉRATIONS
POUR UNE
VISUALISATION
Repère global ->
repère observateur
Projection parallèle
Projection
en perspective
IMPLANTATION
DANS LES
LIBRAIRES
GRAPHIQUES
Pour afficher un objet sur un écran graphique, on effectue un changement de repère de manière à transformer en "coordonnées écran" les coordonnées de l’objet connues dans le repère global (repère de modélisation).
On passe ainsi dans un premier temps de coordonnées globales de modélisation dans R3 à des coordonnées
"observateur" dans R3 (repère lié à la caméra de visualisation).
Dans un second temps, ces coordonnées
observateur sont transformées par projection en coordonnées "écran" dans R3 pour l'affichage (repère lié
à la fenêtre d'affichage).
En coordonnées écran, si l'élimination des parties cachées n'est pas utilisée, une des trois coordonnées
(généralement z) est ignorée. Dans le cas contraire, une des coordonnées (généralement z) fournit l'information
de "profondeur écran" permettant de déterminer si un objet est "devant" un autre objet.
On effectue une "projection" car on réalise une transformation ayant pour but de projeter la silhouette d'un objet sur un écran virtuel placé entre l'objet et l'observateur (appelé aussi centre de projection).
Différents types de projections:
- les projections planaires (écran de projection plan),
- les projections non planaires (écran de projection non plan).
Hypothèses préliminaires
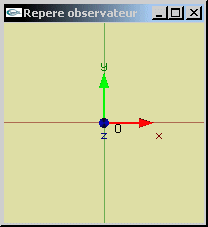
Le plan xz du repère global est le plan de l’horizontale (x vers la droite, z vers l'arrière).
L’axe y est la verticale (orientée vers le haut).
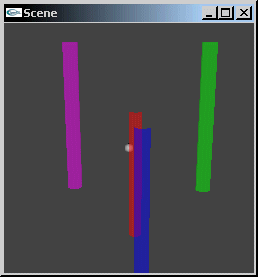
Problème: Visualiser une scène selon un point de vue particulier tel que par exemple défini par la position et l'orientation de l'observateur.
Deux changements de repère successifs:
-
Un premier pour obtenir le point de vue souhaité dans un repère intermédiaire: le repère de l'observateur (il en est l'origine, l'axe -Oz est son axe de vision). Ce repère intermédiaire reste orthonormé (comme le repère global).
-
Un second pour permettre la réalisation de la projection d'affichage. Le repère peut alors ne plus être orthonormé. C'est par exemple à cette étape que l'on réalise une éventuelle projection en perspective.
Types de projections planaires
L'écran de projection est plan. On utilise généralement un des deux modes de projection:
- parallèle,
- en perspective.
Les projections parallèles sont caractérisées par un centre de projection (position virtuelle de l'observateur) situé à l'infini. Ceci a pour conséquence:
- l’existence d'un axe unique de projection et le parallélisme de tous les vecteurs décrivant les projections des points du repère observateur,
- l'indépendance entre la taille d'un objet une fois projeté et sa position dans la scène (pas d'interprétation intuitive de la distance à l'observateur, comparaison triviale des tailles respectives des objets).
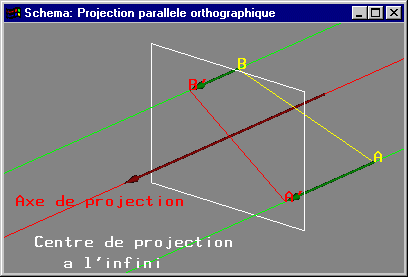
La projection parallèle la plus classique est la projection parallèle orthographique où l'axe de projection est orthogonal au plan de projection.
|
Projection parallèle orthographique |
|
|
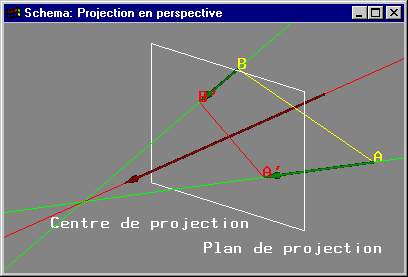
Dans le cas des projections en perspective le centre de projection (la position de l'observateur) n'est pas situé à l'infini. On n'a donc pas d'axe de projection unique.
|
Projection en perspective |
|
|
Propriétés particulières des projections
Non exhaustivement:
-
Les projections parallèles conservent les parallélismes présents dans la scène affichée! En revanche, le dessin en perspective ne conserve pas systématiquement les parallélismes.
-
Les représentations en perspective assurent qu’un objet n fois "plus loin" de l'observateur qu’un autre de taille identique apparaît n fois "plus petit" à l'écran. Les projections parallèles assurent qu'un objet conserve la même taille à l'écran quelle que soit sa position dans la scène.
-
Les représentations en perspective ne conservent pas systématiquement la rectitude des lignes droites.
-
Aucun de ces modes ne conserve les angles.
-
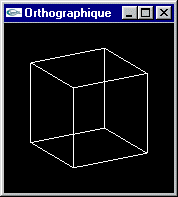
Une représentation en perspective est beaucoup plus proche de la réalité perçue par l’œil qu’une représentation en projection parallèle (surtout pour les objets proches de l’observateur où les déformations sont très importantes).
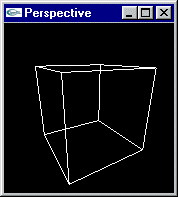
|
Squelette d’un cube vu de face et de très près |
|
|
|
Projection orthographique en haut, |
|
|
Opérations à réaliser pour une visualisation
Les opérations à mettre en œuvre pour visualiser un objet sont:
-
Création d'une représentation de cet objet dans le repère global
-> Modélisation (en particulier modélisation géométrique) de la scène -
Application de la transformation géométrique permettant de transformer les coordonnées de l'objet du repère global vers le repère intermédiaire (repère de l'observateur)
-> Placement et orientation d'une caméra de visualisation -
Application de la transformation géométrique transformant les coordonnées de l'objet depuis le repère de l'observateur vers les coordonnées écran (R3)
-> Choix du type d'"optique" de la caméra de visualisation -
Affichage par suppression d'une des coordonnées 3D (usuellement z)
-> Projection
-> Cadrage écran
-> Elimination des parties cachées (dernière utilisation de z) ou non et algorithmes de rendu
Changement du repère global vers le repère de l'observateur
Une matrice de transformation en coordonnées homogènes nous permet de transformer des coordonnées globales en coordonnées dans le repère de l'observateur.
Les informations connues sur l'observateur (localisation et orientation) nous permettent de calculer cette matrice.
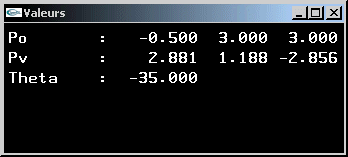
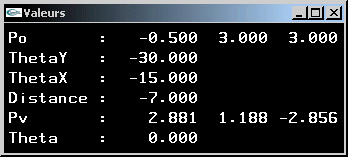
Soit la position Po = ![]() de l'observateur dans le repère global.
de l'observateur dans le repère global.
Les informations permettant de calculer l'orientation de l'observateur peuvent être de différents ordres:
-
la position Pv =
 d'un point directement observé (la position d'un point qui devra se trouver sur le demi axe -Oz après le changement de repère)
et un angle de rotation q autour de l'axe (Po,Pv) (considéré par rapport à une position
de référence, la verticale par exemple),
d'un point directement observé (la position d'un point qui devra se trouver sur le demi axe -Oz après le changement de repère)
et un angle de rotation q autour de l'axe (Po,Pv) (considéré par rapport à une position
de référence, la verticale par exemple),
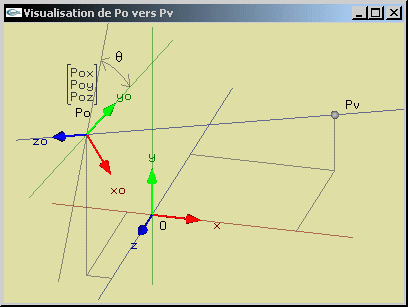
|
Changement de repère pour la visualisation |
|
|
-
3 angles de rotation q1, q2 et q3 ne portant pas successivement deux à deux sur le même axe (permettant donc de définir toute orientation dans l'espace),
-
d'autres informations.
Pour une visualisation proche de celle réalisée par la posture humaine, on adopte fréquemment une transformation telle que les verticales soient conservées.
Un vecteur initialement vertical (x = 0, z = 0) sera vertical après transformation et projection sur l'écran (x = 0).
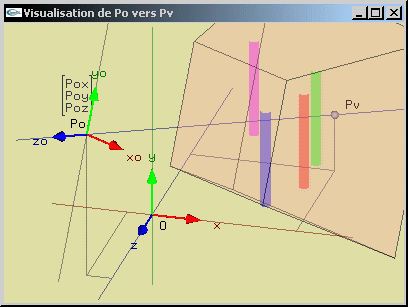
|
Changement de repère pour la visualisation avec conservation des verticales |
|
|
Une première matrice de transformation
On connaît Po et trois rotations d'angle qy autour de Oy, qx autour de Ox, qz autour de Oz intervenant dans cet ordre dans le repère global pour fixer l'orientation de l'observateur.
Le calcul de la matrice de transformation est trivial. Il s'agit du produit matriciel des 4 matrices T, Ry, Rx et Rz.
T est la translation de 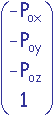 déplaçant Po en l'origine.
déplaçant Po en l'origine.
M = Rz.Rx.Ry.T
=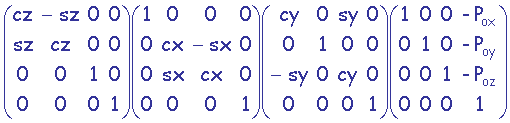
Une deuxième matrice de transformation
On connaît Po, Pv et on désire conserver verticales les verticales (axes orientés en y dans le repère global).
Po est ramené à l'origine par une translation T = 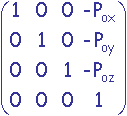 .
.
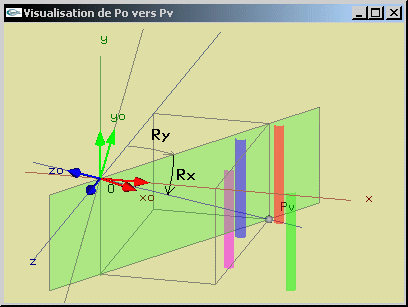
Problème: Trouver les rotations qu'il faut effectuer pour amener le point Pv sur le demi axe -Oz tout en conservant "vertical" tout vecteur "vertical".
On effectue tout d'abord une rotation Ry d'angle qy par rapport à l'axe Oy, puis ensuite une rotation Rx d'angle qx par rapport à Ox.
|
Transformations géométriques pour la visualisation avec conservation des verticales |
|
|
| Rx.Ry | = | 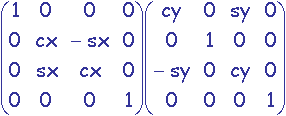
|
| = | 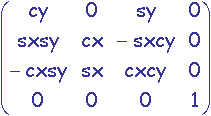
|
Verticalités?
Le vecteur  est obtenu par produit du vecteur
est obtenu par produit du vecteur ![]() (x=z=0 -> vecteur vertical) par la matrice Rx.Ry. La coordonnée x est égale à 0 quels que soient y,
qx et qy
(x=z=0 -> vecteur vertical) par la matrice Rx.Ry. La coordonnée x est égale à 0 quels que soient y,
qx et qy
-> Le vecteur est vertical dans le repère observateur.
On a donc M = Rx.Ry.T =
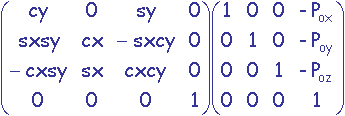
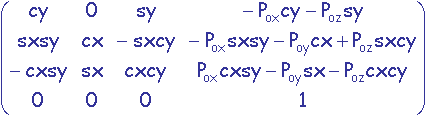
Problème: Déterminer les valeurs de cos(qy), sin(qy), cos(qx) et sin(qx) pour connaître parfaitement M.
![]() =
= ![]() vecteur normé dirigé de Po vers Pv.
vecteur normé dirigé de Po vers Pv.
On établit ![]() =
= 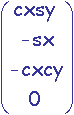 ->
->
M =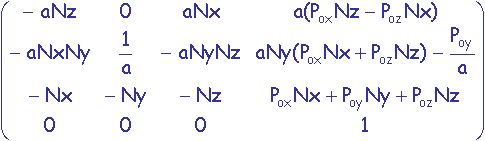
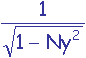
avec a = ![]() =
= 
Il est à noter qu'au moyen de cette formulation, on définit la position de l'observateur et sa direction de visée par son vecteur "regard".
Représentation en projection parallèle orthographique
Les coordonnées projetées  d'un sommet
d'un sommet ![]() du repère global sont trouvées en le multipliant par la matrice précédente.
du repère global sont trouvées en le multipliant par la matrice précédente.
Pour réaliser l'affichage, on utilise directement les coordonnées xpar et ypar obtenues après mise à l'échelle. zpar fournit la profondeur écran si elle est nécessaire.
Soit un plan de projection Pproj orthogonal à l'axe de visé -Oz.
Chaque point Pp = (xp,yp) projection d'un sommet P sur Pproj sera l'intersection entre (P,O) et le plan Pproj.
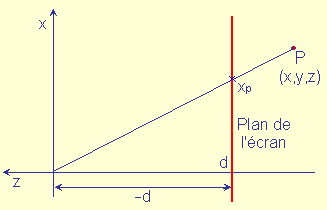
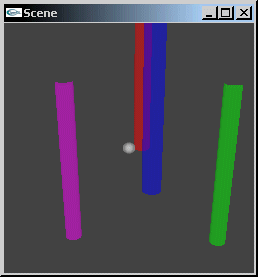
Vue selon l'axe des y
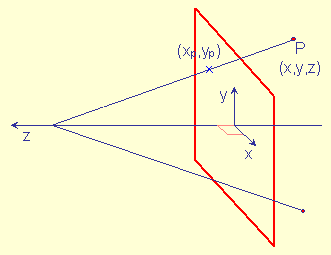
Vue selon un point de vue arbitraire
Soit d la position en z du plan de projection (d < 0.0, -d = distance en z entre O et Pproj),
-> xp = ![]() et yp =
et yp = ![]() .
.
On considère w = ![]() ,
,
-> xp = ![]() et yp =
et yp = ![]() .
.
w est calculé avec la matrice Mper = 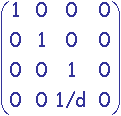 qui appliquée à P =
qui appliquée à P = ![]() permet de trouver
permet de trouver ![]() .
.
Pour connaître la position de projection en perspective d'un point P = ![]() du repère global, on le multipliera par la matrice produit de M par Mper:
du repère global, on le multipliera par la matrice produit de M par Mper:
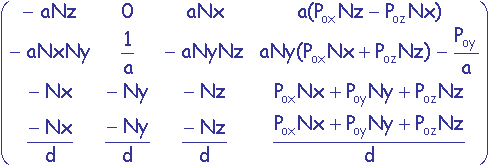
pour obtenir le point de coordonnées ![]() .
.
On divisera ensuite x' par w, y' par w et on utilisera ces valeurs comme x et y à l'écran. z' fournit directement la profondeur écran.
![]()
Implantation généralement constatée au sein des librairies graphiques 3D
Deux niveaux de modélisation pour la construction d'une visualisation:
- la modélisation de la scène,
- la modélisation de la "caméra" qui va visualiser la scène.
Utilisation explicite ou implicite de matrices de transformation pour chacune de ces phases.
Possibilité de changer chacune de ces phases indépendamment de l'autre.