Correction examen
de TD n°1 2011-2012
3 novembre 2011 - 1h15
![]()
|
Correction examen |
|
|
3 novembre 2011 - 1h15 |
|
|
|
|
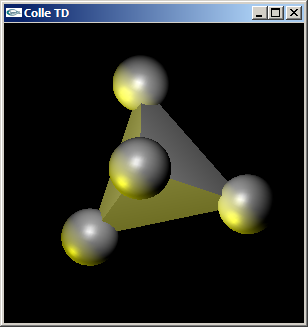
Les fonctions materiel, lumieres, spheres et tetraedre implante les questions 1, 2, 3 et 4.
La question 5 est traitée dans la fonction reshape (la distance entre la caméra et la scène est égale à sqrt(20.0*20.0+20.0*20.0+10.0*10.0) = sqrt(900.0) = 30.0).
/* Examen de TD n°1 2011-2012 */
/* */
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Novembre 2011 */
#include <stdio.h>
#include <math.h>
#include <GL/glut.h>
#include <GL/gl.h>
#include <GL/glu.h>
/* Variables et constantes globales */
#ifndef M_PI
#define M_PI 3.14159
#endif
static int aff = 1;
/* Fonction d'initialisation des parametres */
/* OpenGL ne changeant pas au cours de la vie */
/* du programme */
void init(void) {
glDepthFunc(GL_LESS);
glEnable(GL_DEPTH_TEST);
glEnable(GL_NORMALIZE);
glEnable(GL_AUTO_NORMAL);
glEnable(GL_CULL_FACE);
}
/* Scene dessinee */
static void materiel(void) {
GLfloat diff[4] = { 0.6F,0.6F,0.6F,1.0F };
glMaterialfv(GL_FRONT,GL_DIFFUSE,diff);
GLfloat spec[4] = { 0.4F,0.4F,0.4F,1.0F };
glMaterialfv(GL_FRONT,GL_SPECULAR,spec);
glMaterialf(GL_FRONT,GL_SHININESS,40.0F);
GLfloat ambi[4] = { 0.0F,0.0F,0.0F,1.0F };
glMaterialfv(GL_FRONT,GL_AMBIENT,ambi);
}
static void lumieres(void) {
glEnable(GL_LIGHTING);
{ glEnable(GL_LIGHT0);
const GLfloat light0_position[] = { -4.0,-2.0,-3.0,1.0 };
glLightfv(GL_LIGHT0,GL_POSITION,light0_position);
const GLfloat blanc[] = { 1.0F,1.0F,1.0F,1.0F };
glLightfv(GL_LIGHT0,GL_DIFFUSE,blanc);
glLightfv(GL_LIGHT0,GL_SPECULAR,blanc);
const GLfloat noir[] = { 0.0F,0.0F,0.0F,1.0F };
glLightfv(GL_LIGHT0,GL_AMBIENT,noir); }
{ glEnable(GL_LIGHT1);
const GLfloat light1_position[] = { 1.5,-1.0,-1.0,0.0 };
glLightfv(GL_LIGHT1,GL_POSITION,light1_position);
const GLfloat jaune[] = { 1.0F,1.0F,0.0F,1.0F };
glLightfv(GL_LIGHT1,GL_DIFFUSE,jaune);
glLightfv(GL_LIGHT1,GL_SPECULAR,jaune);
const GLfloat noir[] = { 0.0F,0.0F,0.0F,1.0F };
glLightfv(GL_LIGHT1,GL_AMBIENT,noir); }
}
static void spheres(void) {
const float p[4][3] =
{ { 0.0F, 0.0F, 0.0F },
{ 4.0F, 0.0F, 0.0F },
{ 0.0F, 4.0F, 0.0F },
{ 0.0F, 0.0F, 4.0F } };
glPushMatrix();
for ( int i = 0 ; i < 4 ; i++ ) {
glPushMatrix();
glTranslatef(p[i][0],p[i][1],p[i][2]);
glutSolidSphere(1.0,36,36);
glPopMatrix(); }
glPopMatrix();
}
static void tetraedre(void) {
const float p[4][4] =
{ { 0.0F, 0.0F, 0.0F, 1.0F },
{ 4.0F, 0.0F, 0.0F, 1.0F },
{ 0.0F, 4.0F, 0.0F, 1.0F },
{ 0.0F, 0.0F, 4.0F, 1.0F } };
glPushMatrix();
glBegin(GL_TRIANGLES);
glNormal3f(0.0F,0.0F,-1.0F);
glVertex3fv(p[2]);
glVertex3fv(p[1]);
glVertex3fv(p[0]);
glNormal3f(0.0F,-1.0F,0.0F);
glVertex3fv(p[3]);
glVertex3fv(p[0]);
glVertex3fv(p[1]);
glNormal3f(-1.0F,0.0F,0.0F);
glVertex3fv(p[3]);
glVertex3fv(p[2]);
glVertex3fv(p[0]);
float n =(float) (sqrt(3.0)/3.0);
glNormal3f(n,n,n);
glVertex3fv(p[1]);
glVertex3fv(p[2]);
glVertex3fv(p[3]);
glEnd();
glPopMatrix();
}
void scene() {
glPushMatrix();
materiel();
lumieres();
spheres();
tetraedre();
glPopMatrix();
}
/* Fonction executee lors d'un rafraichissement */
/* de la fenetre de dessin */
void display(void) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPolygonMode(GL_FRONT_AND_BACK,(aff) ? GL_FILL : GL_LINE);
glPushMatrix();
scene();
glPopMatrix();
glFlush();
glutSwapBuffers();
int error = glGetError();
if ( error != GL_NO_ERROR )
printf("Erreur OpenGL: %d\n",error);
}
/* Fonction executee lors d'un changement */
/* de la taille de la fenetre OpenGL */
/* -> Ajustement de la camera de visualisation */
void reshape(int x,int y) {
glViewport(0,0,x,y);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(2*asin(5.0/30.0)*180.0/M_PI,(float) x/y,25.0,35.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(-19.0,-19.0,-9.0,1.0,1.0,1.0,0.0,1.0,0.0);
}
/* Fonction executee lors de la frappe */
/* d'une touche du clavier */
void keyboard(unsigned char key,int x,int y) {
switch ( key ) {
case 0x20 :
aff = (aff+1)%2;
glutPostRedisplay();
break;
case 0x1B :
exit(0);
break; }
}
/* Fonction principale */
int main(int argc,char **argv) {
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_RGBA|GLUT_DEPTH|GLUT_DOUBLE);
glutInitWindowSize(300,300);
glutInitWindowPosition(50,50);
glutCreateWindow("Colle TD");
init();
glutKeyboardFunc(keyboard);
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutMainLoop();
return(0);
}
Exercice supplémentaire
Les transformations géométriques sont, dans l'ordre chronologique, le zoom Z,
la rotation R et la translation T.
La transformation globale est obtenue par le produit T.R.Z (matrices dans l'ordre inverse de l'ordre chronologique).
Après multiplication des matrices canoniques, le résultats est:
T.R.Z =
 .
. .
. =
=
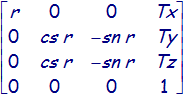
|
|
|
Quelques indications sur l'évaluation Les exercices 1 à 5 ont le même coefficient dans la note globale de l'examen. L'exercice supplémentaire sera intégré en "points en plus" dans la note globale
du module. |
|
|
|
Remarques, erreurs |