Examen de TD n°1 2011-2012
3 novembre 2011 - 1h15
![]()
![]()
Seuls les supports de cours HTML et les notes manuscrites de TD sont autorisés.
Les dispositifs électroniques sont interdits.
On n'oubliera pas de fournir quelques commentaires sur les techniques employées.
Question 1: Modélisation OpenGL
On donne les 4 sommets de coordonnées (0.0, 0.0, 0.0), (4.0, 0.0, 0.0), (0.0, 4.0, 0.0) et (0.0, 0.0, 4.0).
Ecrire une fonction C de modélisation OpenGL permettant de créer la scène constituée de 4 sphères de rayon 1.0 centrées sur ces 4 sommets.
Question 2: Modélisation par facettes en OpenGL
On donne les 4 sommets de coordonnées (0.0, 0.0, 0.0), (4.0, 0.0, 0.0), (0.0, 4.0, 0.0) et (0.0, 0.0, 4.0).
Ecrire une fonction C - OpenGL permettant de modéliser par facettes le tétraèdre à faces triangulaires formé par ces 4 sommets. On spécifiera les normales de manière que l'éclairage du tétraèdre soit possible.
Question 3: Lumières en OpenGL
On souhaite éclairer une scène au moyen de 2 lumières. La première est blanche tant en diffus qu'en spéculaire. La seconde est jaune tant en diffus qu'en spéculaire. Aucune des deux n'a de composante ambiante. La première est ponctuelle et est placée en position (-4.0, -2.0, -3.0). La seconde est directionnelle et est orientée pour éclairer selon la direction d'incidence (-1.5, 1.0, 1.0).
Ecrire les lignes de code OpenGL permettant de configurer et d'activer ces deux lumières en utilisant les lumières OpenGL 0 et 1.
Question 4: Matériel en OpenGL
On souhaite afficher une scène en utilisant un matériel:
- diffusant selon les coefficients (0.6, 0.6, 0.6),
- réfléchissant spéculairement selon les coefficients (0.4, 0.4, 0.4) avec pour réflectivité 40.0,
- ne répondant pas aux éclairages ambiants,
- n'ayant pas de composante émissive.
Ecrire les lignes de code OpenGL permettant de configurer un tel matériel.
Question 5: Caméra en OpenGL
On considère une scène centrée sur le point de coordonnées (1.0, 1.0, 1.0). Elle occupe un volume "sphérique" de rayon voisin de 5.0. On souhaite la visualiser au moyen d'une caméra placée en position (-19.0, -19.0, -9.0). On souhaite de plus que la projection soient réalisée en perspective de manière que la scène "rentre" verticalement en gros plan dans la fenêtre de visualisation.
Définir les paramètres de gluLookAt que vous utiliseriez.
Définir les paramètres de gluPerspective que vous utiliseriez.
Question "bonus": Mathématiques matricielles
On donne les matrices de transformation canoniques de rotation d'angle qx autour de l'axe x passant par l'origine, de translation de vecteur (Tx, Ty, Tz) et de zoom uniforme de rapport r:
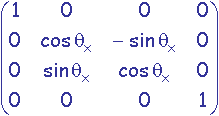 ,
,
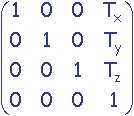 ,
, 
On rappelle la formule du produit matriciel: mij =
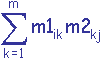 pour i et j compris entre 1 et 4 et m = 4.
pour i et j compris entre 1 et 4 et m = 4.![]()
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr