Examen de TD n°2 2012-2013

RETOUR

17 décembre 2012 - 1h35

Sujet (pdf)

Tous les supports papier sont autorisés.
Les dispositifs électroniques (ordinateur, tablette, téléphone mobile, ...) sont interdits.
On n'oubliera pas de fournir quelques commentaires sur les techniques employées.

Question 1: Brésenham

L'algorithme "classique" de Bresenham (ci-contre) permet de tracer un segment de droite défini entre 2 sommets de coordonnées entières 2D (xi,yi) et (xf,yf). Si ces coordonnées sont telles que abs(xi-xf) > abs(yf-yi), la suite de pixels tracée présente une ou plusieurs situations où plusieurs pixels sont allumés sur une même trame horizontale.
Adapter cet algorithme pour n'allumer qu'un seul pixel à chaque trame horizontale et pour que, à l'exception des trames yi et yf où les pixels (xi,yi) et (xf,yf) sont allumés, le pixel allumé sur une trame soit le pixel central de tous les pixels candidats sur cette trame.

 void ligne(int xi,int yi,
           int xf,int yf) {
  int dx,dy,i,xinc,yinc,cumul,x,y;
  x = xi;
  y = yi;
  dx = xf - xi;
  dy = yf - yi;
  xinc = ( dx > 0 ) ? 1 : -1;
  yinc = ( dy > 0 ) ? 1 : -1;
  dx = abs(dx);
  dy = abs(dy);
  allume_pixel(x,y);
  if ( dx > dy ) {
    cumul = dx / 2;
    for ( i = 1 ; i <= dx ; i++ ) {
      x += xinc;
      cumul += dy;
      if ( cumul >= dx ) {
        cumul -= dx;
        y += yinc; }
      allume_pixel(x,y); } }
    else {
    cumul = dy / 2;
    for ( i = 1 ; i <= dy ; i++ ) {
      y += yinc;
      cumul += dx;
      if ( cumul >= dy ) {
        cumul -= dy;
        x += xinc; }
      allume_pixel(x,y); } }
}

Question 2: Cohen-Sutherland

L'algorithme de Cohen-Sutherland s'applique usuellement au clipping d'un segment de droite 2D dans un rectangle 2D à cotés parallèles aux axes.
Décrire, sans la développer sous forme de code informatique, une généralisation de cet algorithme au clipping d'un segment de droite à l'intérieur d'un quadrilatère (polygone à 4 cotés) quelconque.

Question 3: Mathématiques

On considère un polygone à n sommets (S0 à Sn-1) définis en trois dimensions.
Décrire une méthode mathématique permettant de tester si ce polygone est plan.

Question 4: Modélisation OpenGL

L'obtention d'un rendu d'éclairage de bonne qualité se heurte fréquemment en OpenGL 1.x à l'impossibilité de générer des détails d'affichage de taille inférieure à la taille des facettes. Une solution peut être alors de générer plus de facettes.
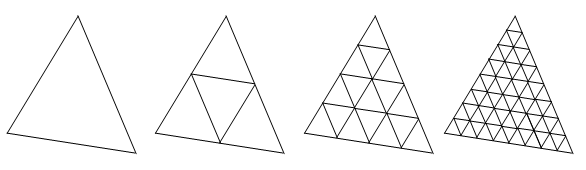
On considère une facette F triangulaire 3D définie par ses trois sommets S1, S2 et S3. Développer une fonction d'affichage OpenGL de prototype void affichageFacette(int n, Position3D *S1, Position3D *S2, Position3D *S3); permettant l'affichage de la facette (S1, S2, S3), décomposée au niveau n de précision (n >= 0) en un ensemble de facettes triangulaires situées dans le plan de F selon le schéma ci-contre (n = 0, 1, 2, 3 de gauche à droite, multiplication par 4 du nombre de facettes à chaque niveau supplémentaire).

On rappelle que la classe Position3D comporte un champ c de type tableau de 4 réels double précision permettant le stockage de coordonnées 3D en "coordonnées homogènes".

Correction

Remarques, erreurs
nicolas.janey@univ-fcomte.fr