Session 2 2004-2005
![]()
On n'oubliera pas de fournir quelques explications sur les techniques employées.
Question 1: Animation en OpenGL
On considère une scène constituée d'un ensemble d'objets immobiles éclairés par deux lumières en mouvement. Les objets sont modélisés au sein d'une fonction void objets(void) quelconque. Les lumières possèdent les caractéristiques suivantes:
- Lumière n°1 : Lumière ponctuelle rouge en réflexion diffuse et bleue en réflexion spéculaire se déplaçant par aller et retour à vitesse uniforme entre les positions (10.0, 0.0, 10.0) et (-10.0, 0.0, 10.0) en 200 images pour un aller et retour,
- Lumière n°2 : Lumière directionnelle jaune en réflexion diffuse et magenta en réflexion spéculaire tournant à vitesse uniforme dans le plan yz à raison de 2° de rotation entre chaque image.
Ecrire les fonctions idle et display correspondant à cette animation.
Question 2: Modélisation fil de fer en OpenGL
On considère la structure de données suivantes:
struct Coord2D {
float x;
float y; };
struct Polygone2D {
struct Coord2D *p;
int nbp; };
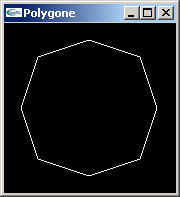
Une variable de type Coord2D représente une position dans un espace à 2 dimensions. Une variable de type Polygone2D représente un polygone de nbp sommets stockés dans le tableau p.
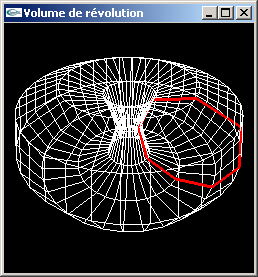
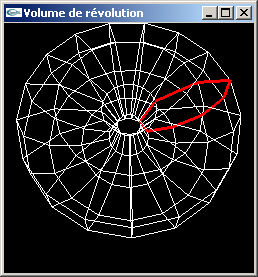
Spécifier et écrire une fonction OpenGL permettant de modéliser en fil de fer le "volume de révolution" créé par rotation d'un polygone autour de l'axe Oy.
Question 3: Algorithmique de l'infographie
a) Programmer une fonction de dessin de segment de droite permettant de dessiner des segments avec un motif de tracé sur 16 bits.
Exemple: Le motif 1111000110000100 générera un segment alternant cycliquement le motif constitué de 4 pixels allumés, puis 3 pixels inchangés, puis 2 pixels allumés, puis 4 pixels inchangés, puis 1 pixel allumé et enfin 2 pixels inchangés.
b) Proposer une évolution de l'algorithme de Bresenham pour le tracé de segment de droite permettant de tracer en 4-connexité et non en 8-connexité.
Question 4: Mathématiques de l'Infographie
On considère une direction normée (dx, dy, dz) d'un espace 3D.
On considère une position (px, py, pz) d'un espace 3D.
Calculer les coefficients a, b, c et d du plan P d'équation cartésienne ax+by+cz+d = 0 tel que la position (px, py, pz) est incluse dans P et que la direction (dx, dy, dz) est orthogonale à P.
Question 5: Modèles d'illumination
a) Définir les structures de données permettant de représenter les informations
suivantes:
- une direction dans un espace à trois dimensions,
- une couleur rvb,
- une énergie lumineuse colorée,
- une source lumineuse directionnelle colorée,
- un matériel avec gestion de réflexion diffuse.
b) On considère une surface munie d'un matériel. On considère un point sur cette surface. On connaît la normale à la surface en ce point. Spécifier et écrire une fonction permettant de calculer la quantité d'énergie lumineuse colorée diffusée (formule de Lambert) au niveau de ce point sous l'éclairage d'une source lumineuse directionnelle.
![]()
Remarques, erreurs
nicolas.janey@univ-fcomte.fr