Session 2 2004-2005

RETOUR

Vendredi 14 janvier 2005 - 2h

Question 1: Lumières animées

• Une seule variable globale est utilisée: un compteur d'images.
• Les appels non récurrents à glLight (concernant les caractéristiques autres des positions ou des directions) peuvent être réalisés dans la fonction display ou mieux, dans une fonction init appelée une fois avant le glutMainLoop.
• Les appels récurrents à glLight (concernant les caractéristiques de position ou de direction) doivent être réalisés dans la fonction display avant l'appel à la fonction objets.
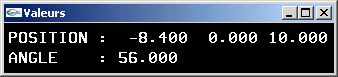
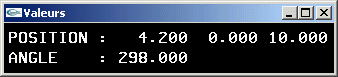
  L'animation portant sur la position de la lumière ponctuelle et la direction de la lumière directionnelle, les appels correspondant à glLight doivent être précédés des glTranslate et glRotate nécessaires. Chacun de ces appels doit en outre être encadré d'un glPushMatrix, glPopMatrix pour ne porter que sur la lumière et pas sur les définitions ultérieures.
• La lumière numéro x est définie comme une lumière ponctuelle par un appel à glLightfv(GL_LIGHTx, GL_POSITION, pos). pos est un tableau à 4 valeurs de type float. Les trois premières donnent la position de la lumière. La dernière doit avoir 1.0F pour valeur.
• La lumière numéro x est définie comme une lumière directionnelle par un appel à glLightfv(GL_LIGHTx, GL_POSITION, pos). pos est un tableau à 4 valeurs de type float. Les trois premières donnent la direction de la lumière. La dernière doit avoir 0.0F pour valeur.
• Dans la fonction idle, on n'oubliera pas d'utiliser glutPostRedisplay ou glutPostWindowRedisplay pour poster un ordre de réaffichage de l'image après modification du compteur d'images.

LumieresAnimees
Fichier source complet : LumieresAnimees.cpp
Modules utilitaires: Modules.zip

Question 2: Modélisation fil de fer d'un volume de révolution

• Le volume de révolution est dessiné:
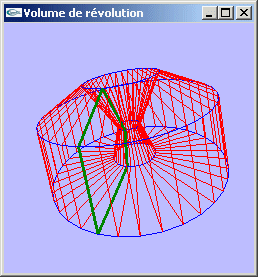
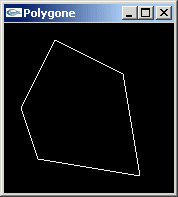
  (1) en traçant n fois le polygone avec une rotation de n/360.0F° autour de l'axe Oy entre chaque tracé (ci-dessous, tracés en rouge),
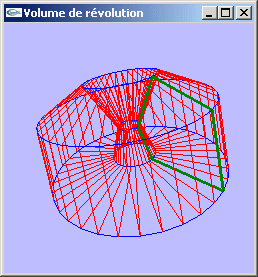
  (2) en reliant en cercle chacune des positions consécutives de chacun des points du polygone (ci-dessous, tracés en bleu).
• Tant dans le cas (1) que dans le cas (2), les primitives graphiques utilisées sont des boucles de segments de droite : GL_LINE_LOOP.
• Pour optimiser les calculs numériques, les coordonnées de l'ensemble des sommets utilisés sont calculées dans un premier temps et stockées dans un tableau. Puis le tableau est utilisé pour modéliser les primitives graphiques.
• Les sommets de modélisation sont calculés par implantation de la matrice de transformation correspondant à chacune des rotations autour de l'axe y (en coordonnées homogènes) et produit de chaque sommet du polygone (casté en coordonnées homogènes) par chacune de ces matrices.

VolumeRevolution
Fichier source complet : VolumeRevolution.cpp
Modules utilitaires: Modules.zip

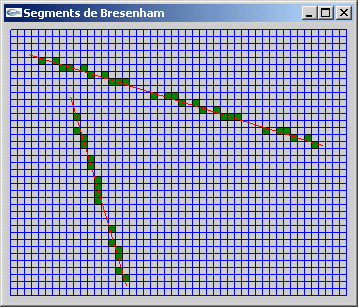
Question 3: Variantes de l'algorithme de Bresenham pour le tracé de segments

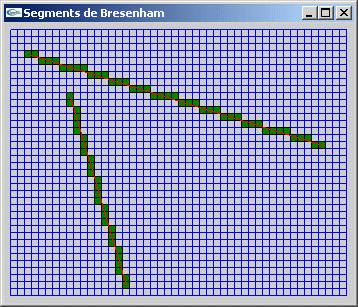
• Le motif de tracé est stocké dans un entier. Chaque bit caractérise une information booléen (vrai -> afficher, faux -> ne pas afficher). Les bits sont extraits par décalage des bits d'information vers la droite et utilisation du masque binaire 0x0001.
  La boucle générale de tracé itère sur i. le modulo 16 de cette valeur nous indique le bit à tester pour décider de tracer un pixel ou non.

• Au cours de l'exécution de l'algorithme, chaque fois qu'un décalage en x et en y sont réalisés au cours de la même itération pour aller tracer un pixel dans un des quatre coins d'un autre pixel, il faudra allumer en plus un second pixel pour obtenir la 4-connexité.
  Si on considère la position (x, y) du pixel initial et la position (x+xi, y+yinc) du nouveau pixel tracé, deux positions candidates existent pour le pixel supplémentaire: (x+xi, y) et (x, y+yinc).
  Le choix entre ces deux positions est réalisé pour coller au plus près du segment continu. Pour cela, on utilise cumul qui, s'il est supérieur à la moitié de sa valeur d'incrément, conduira au choix d'une des positions candidates et à l'autre sinon.

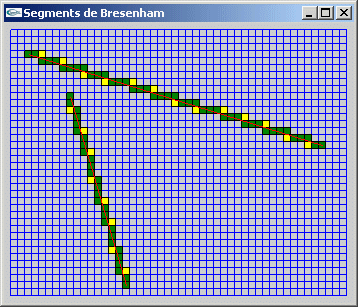
SegmentsBresenham
Fichier source complet : SegmentsBresenham.cpp
Modules utilitaires: Modules.zip

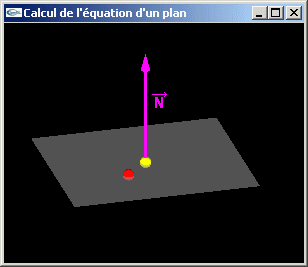
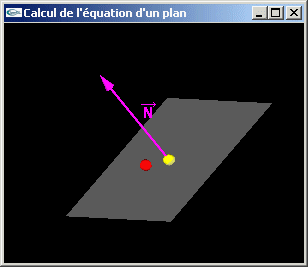
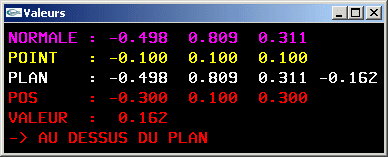
Question 4: Calcul de l'équation cartésienne d'un plan

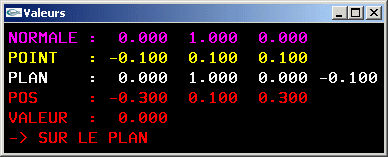
• Si le vecteur a pour coordonnées (dx, dy, dz) et le point p a pour coodonnées (px, py, pz), alors, l'équation ax + by + cz + d = 0 définissant le plan doit vérifier a = dx, b = dy, c = dz et d = -(dxpx+dypy+dzpz).
• Démontration:
  Tout vecteur du plan peut être considéré comme allant du point p à un autre point du plan de coordonnées (x, y, z) vérifiant ax + by + cz + d = 0 (1)
  -> Ce vecteur a comme coordonnées (x-px, y-py, z-pz).
  Or, s'il appartient au plan, ce vecteur doit être orthogonal au vecteur normal au plan.
  -> le produit scalaire entre ces deux vecteurs doit être égal à 0.
  -> (x-px)dx + (y-py)dy + (z-pz)dz = 0
  -> dx x + dy y + dz z - (pxdx+pydy+pzdz) = 0
  -> Avec l'équation (1), a = dx, b = dy, c = dz et d =-(dxpx+dypy+dzpz)

NormaleVersPlan
Fichier source complet : NormaleVersPlan.cpp
Modules utilitaires: Modules.zip

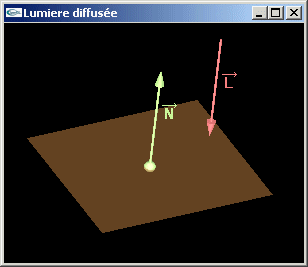
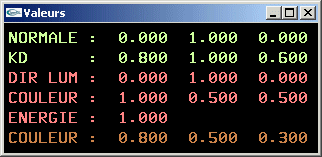
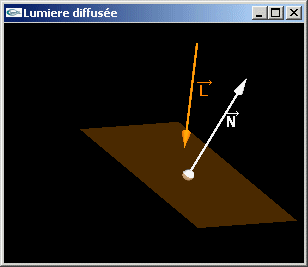
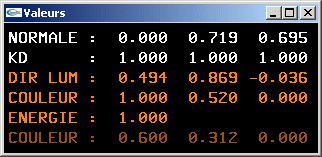
Question 5: Quantité d'énergie diffusée sous l'éclairage d'une lumière directionnelle

• La structure de données direction est définie en coordonnées homogènes pour supporter les transformations géométriques.
• La structure de données couleur peut intégrer ou non un champs alpha. Ses champs r, v et b peuvent être de type entier ou réel avec un intervale de variabilité entre 0 et une valeur maximale donnée (255 en entier 8 bits, 1.0 en réel).
• La structure de données énergie lumineuse colorée comprend les mêmes champs que le structure couleur mais leurs intervales de variabilité courent de 0 à l'infini.
• La structure lumière directionnelle est caractérisée par une direction, une couleur et une intensité. On pourrait aussi la représenter par une direction et une énergie lumineuse colorée.
• Le matériel comporte un champ coefficient de diffusion de type couleur.
• L'énergie lumineuse diffusée en un point d'une surface soumis à l'éclairage d'une source lumineuse directionnelle calculé au moyen de la formule de Lambert dépend du coefficient de diffusion du matériel, de la source lumineuse et de la normale à la surface au point de diffusion.
  La position du point n'a pas d'importance car l'intensité lumineuse reçue depuis une lumière directionnelle est uniforme dans l'espace de la scène (la source est placée "à l'infini").
• Un résultat négatif au calcul du produit scalaire de la formule de Lambert conduit à une intensité diffusée égale à 0.0 pour les composantes rouge, verte et bleue.

DiffusionSousLumiereDirectionnelle
Fichier source complet : DiffusionSousLumiereDirectionnelle.cpp
Modules utilitaires: Modules.zip

Quelques indications sur l'évaluation

Tous les exercices sont affectés du même coefficient.
L'examen est trop long pour être réalisé en une durée de 2h. Il est demandé aux étudiants de réaliser correctement quatre exercices sur cinq.

Remarques, erreurs
nicolas.janey@univ-fcomte.fr