Correction examen
de TD n°2 2004-2005

RETOUR

Jeudi 16 décembre 2004 - 1h25

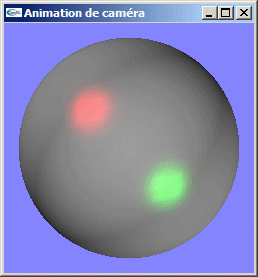
Question 1: Animation de caméra

• Une seule variable globale est absolument nécessaire à la gestion de l'animation:
  la position en x de l'observateur.
  Toutes les autres informations nécessaires à l'affichage peuvent être calculées à partir de cette valeur.
• L'animation à programmer porte sur la position et l'angle d'ouverture de la caméra de projection en perspective. La position est spécifiée via l'utilisation de gluLookAt. L'angle d'ouverture de la caméra (inversement proportionnel à la distance caméra <-> scène) est spécifié en paramètre de gluPerspective.
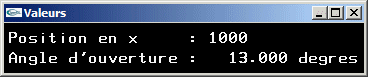
  La scène visualisée possède un diamètre (une taille) voisin de 200 à une distance de 1000. L'angle d'ouverture à cette distance devra être voisin de tan^-1(200/1000) radians qui est voisin de 200/1000 = 0.2 radians (12° ou 13°). A proche distance, les déformations liées à la mise en perspective deviennent très importantes et une simple augmentation de l'ouverture inversement proportionnelle à la distance n'est pas utilisable pour gérer correctement le problème.
• L'animation sur gluPerspective conduit à déplacer cet appel de fonction de sa position naturelle (dans la fonction reshape) à la fonction display.
  -> L'utilisation directe des dimensions de la fenêtre (pour ajuster le ratio de la caméra au ratio de la fenêtre) n'est pas possible car ces valeurs sont acquises en paramètre de reshape. Elles pourront être obtenues soit par l'utilisation de variables globales soit par l'utilisation de glutGet(GLUT_WINDOW_WIDTH) et glutGet(GLUT_WINDOW_HEIGHT).

Les fonctions reshape et display pourraient donc être

static float px = 1000.0F ;
static int fw ;
static int fh ;

void reshape(int w,int h) {
  glViewport(0,0,w,h);
  fw = w;
  fh = h;
}

void display(void) {
  glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);
  glMatrixMode(GL_PROJECTION);
  glLoadIdentity();
  gluPerspective(13.0*1000.0/px,
                 fw/(float)fh,
                 px-110.0F,
                 px+110.0F);
  glMatrixMode(GL_MODELVIEW);
  glLoadIdentity();
  gluLookAt(px,0.0F,0.0F,
            0.0F,0.0F,0.0F,
            0.0F,1.0F,0.0F);
  scene();
  glFlush();
  glutSwapBuffers();
}

• La gestion interactive de l'animation au moyen des flèches haut et bas demande la programmation d'une fonction void special(int k,int x,int y) spécifiée via glutSpecialFunc car ces touches ne correspondent pas à au clavier ascii mais sont des touches spéciales.
  -> On ne peut pas utiliser de fonction void key(unsigned char k,int x,int y) spécifiée via glutKeyFunc.
  On n'oubliera pas d'utiliser glutPostRedisplay ou glutPostWindowRedisplay pour entraîner un nouvel affichage de l'image après modification de la position de la caméra quand k = GLUT_KEY_UP ou GLUT_KEY_DOWN.

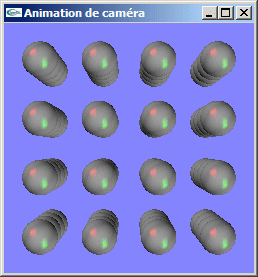
Au plus loin -> peu de déformation

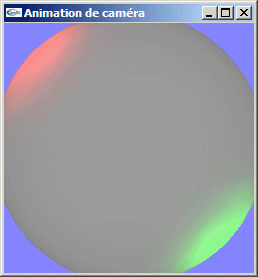
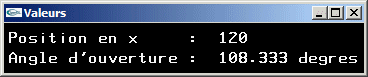
Au plus proche -> déformation très importante

Exam-TD2-2004-2005-Exo1
Fichier source complet : Exam-TD2-2004-2005-Exo1.cpp
Modules utilitaires: Modules.zip

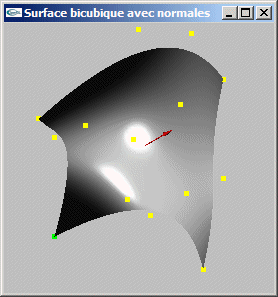
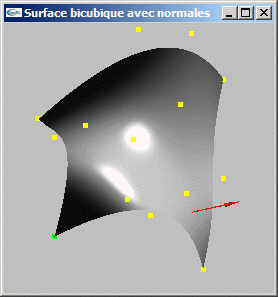
Question 2: Courbes et surfaces paramétriques

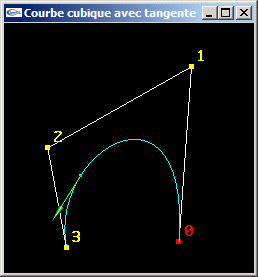
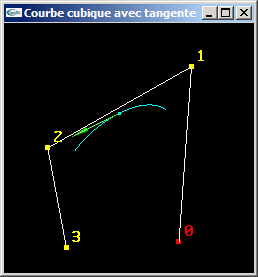
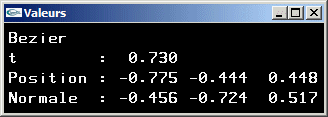
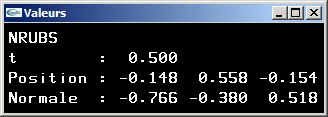
Une méthode pour déterminer la tangente à une courbe paramétrique C(t) consiste à dériver l'équation sur le paramètre t. L'équation est C(t) = (t³ t² t 1).M.G pour les courbes paramétriques cubiques.
Sa dérivé en t est C'(t) = (3t² 2t 1 0).M.G (chacune des composantes de T' est la dérivée en t de la composante correspondante de T).
En un point C(t), le vecteur tangent est donc C'(t). Il est possible de le normer.

Exam-TD2-2004-2005-Exo2a
Fichier source complet : Exam-TD2-2004-2005-Exo2a.cpp
Modules utilitaires: Modules.zip

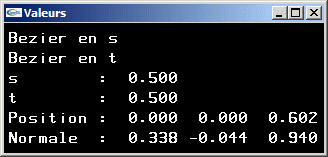
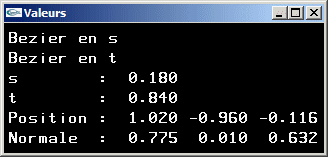
Une méthode pour déterminer la normale à une surface paramétrique S(s,t) consiste:
(1) à calculer une première tangente en dérivant l'équation sur le paramètre s, t restant constant,
-> T₁(s,t) = = 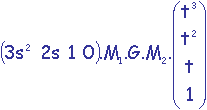pour les surfaces paramétriques bicubiques,
(2) à calculer une seconde tangente en dérivant l'équation sur le paramètre t, s restant constant,
-> T₂(s,t) = =
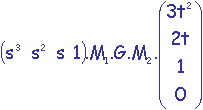
(3) à calculer le produit vectoriel de ces deux tangentes (il est orthogonal aux deux tangentes et donc orthogonal à la surface),
(4) à normer ce produit vectoriel.

Exam-TD2-2004-2005-Exo2b
Fichier source complet : Exam-TD2-2004-2005-Exo2b.cpp
Modules utilitaires: Modules.zip

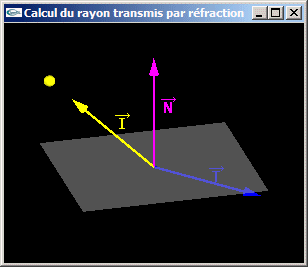
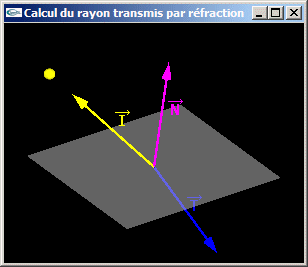
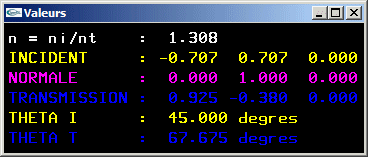
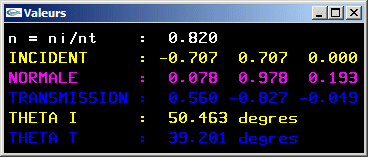
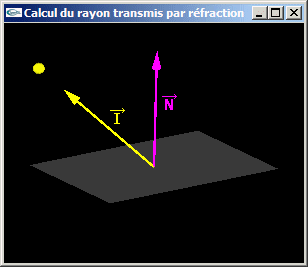
Question 3: Calcul du rayon transmis lors d'une réfraction

• On définit une structure de données pour manipuler des directions (coordonnées homogènes).
• On écrit trois fonctions destinées à:
  • calculer le produit scalaire entre deux directions,
  • multiplier une direction par une valeur numérique,
  • soustraire deux directions.
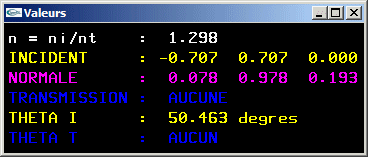
• La fonction à écrire prend en paramètre le rapport n (paramètre de type réel) entre les indices de réfraction des deux milieux, la direction du rayon incident et la direction de la normale à l'interface. Elle rend la direction du rayon transmis s'il existe.
• La fonction intègre le traitement de l'exception où il n'y a pas de transmission.
  Ce cas particulier advient quand la valeur pour laquelle on calcule la racine carrée est négative.
  -> Il n'existe pas de racine carrée.
  -> Il n'y a pas de transmission.
  Cet exception peut être gérée en rendant un booléen pour indiquer s'il y a transmission.

Exam-TD2-2004-2005-Exo3
Fichier source complet : Exam-TD2-2004-2005-Exo3.cpp
Modules utilitaires: Modules.zip

Question 4: Modélisation OpenGL

• Un tétraèdre régulier est un volume à 4 sommets (et 4 faces) tel que les 4 sommets soient à la même distance les uns des autres deux à deux (10 dans l'exercice).
• Détermination des positions des sommets d'un tétraèdre régulier de coté 10.0.
  Il en existe une infinité. -> On en calcul un.
  Le premier sommet est en position (0.0, 0.0, 0.0).
  Le deuxième sommet est placé à une distance de 10.0 en x positif, donc, en position (10.0, 0.0, 0.0).
  Le troisième sommet est placé dans le plan xOy. Les deux possibilités sont (5.0, sqrt(100-25), 0.0) et (5.0, -sqrt(100-25), 0.0). On prend le premier sommet de position (5.0, 5*sqrt(3), 0.0).
  Le quatrième sommet possède un x centré par rapport à ceux des trois autres
  -> (0.0+10.0+5.0)/3.0 = 5.0.
  Le quatrième sommet possède un y centré par rapport à ceux des trois autres
  -> (0.0+0.0+5.0*sqrt(3))/3.0 = 5.0/sqrt(3).
  La coordonnée z du quatrième sommet est établie en le plaçant à la distance 10.0 de l'origine, avec un placement en z négatif ou positif. On choisit en z négatif
  -> z = -sqrt(100.0-5.0*5.0-5.0*5.0/3)
        = -sqrt((300.0-75.0-25.0)/3.0)
        = -10.0*sqrt(2.0)/sqrt(3.0).
  Le centre de ce tétraèdre est en (5.0, 5.0/sqrt(3), -5.0/sqrt(2.0)/sqrt(3.0)).
  Une translation de - ce vecteur centrera le tétraèdre à l'origine.
  Le calcul numérique conduit aux positions suivantes:
    (-5.0, -2.88675, 2.04125)
    (5.0 ,-2.88675 ,2.04125)
    (0.0, 5.7735, 2.04125)
    (0.0, 0.0, -6.12375)
• L'exercice inclut la définition des matériaux et des lumières.
  Pour ces définitions, il est possible de déplacer les appels de fonction OpenGL non récurrents dans une fonction init appelée une seule fois dans la fonction main avant le gluMainLoop. Il s'agit des définitions de lumière ne concernant pas des positions ou des directions. Celles-ci doivent rester dans la fonction display car elles doivent être réalisées dans le même repère que celui de la scène.

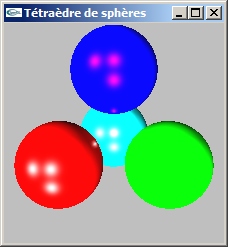
Image obtenue

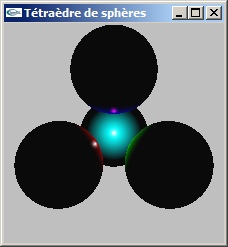
Contribution de la lumière ponctuelle centrale

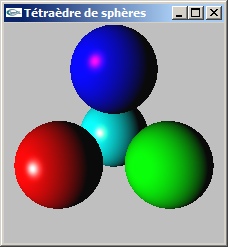
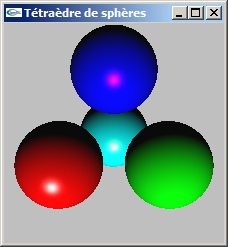
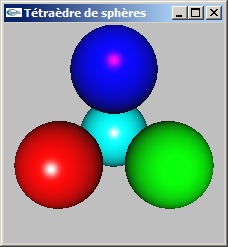
Contributions des lumières directionnelles

Exam-TD2-2004-2005-Exo4
Fichier source complet : Exam-TD2-2004-2005-Exo4.cpp
Modules utilitaires: Modules.zip

Quelques indications sur l'évaluation

Tous les exercices sont affectés du même coefficient.
L'examen est trop long pour être réalisé en une durée de 1h20. Il est demandé aux étudiants de réaliser correctement trois exercices sur quatre.

Remarques, erreurs
nicolas.janey@univ-fcomte.fr