Les fractales, les I.F.S.
Principe
Fractal Brownian
Motion
Julia-Fatou
Mandelbrot
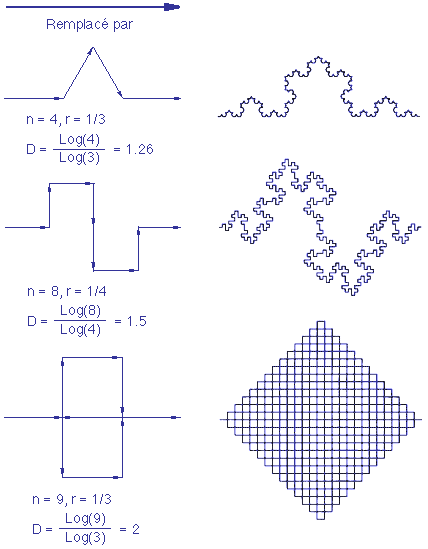
Une approche intuitive consiste à considérer qu'une fractale est la transformation récursive d'un objet par n copies de lui même à l'échelle r (avec r < 1).
Cette propriété est appelée l'autosimilarité.
On a coutume de caractériser un objet fractal à partir d'un paramètre numérique généralement noté D appelé dimension fractale.
D est égal à 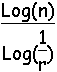 . Il caractérise la manière selon laquelle une fractale évolue dans
l'espace où elle est dessinée. Plus D est grand plus l'évolution est
"chaotique".
. Il caractérise la manière selon laquelle une fractale évolue dans
l'espace où elle est dessinée. Plus D est grand plus l'évolution est
"chaotique".
Fractales déterministes
On appelle fractale déterministe une fractale dont le mode de réplication ne fait pas intervenir de composante aléatoire.
Fractales non déterministes
Les fractales stochastiques, par opposition aux fractales déterministes, permettent de générer des dessins non réguliers.
Pour générer une fractale stochastique, on n'a plus un seul mode de réplication, mais deux ou plusieurs choisis aléatoirement.
On obtient de bons résultats avec D voisin de 1,2 pour générer des rivages océaniques (lignes) et avec D voisin de 2,2 pour la génération de montagnes (surfaces).
Plus D croît plus la ligne ou la surface devient chaotique et irréaliste.
Historiquement: Le bruit brownien fractionnaire (FBM)
Les fractales sont issues des travaux de Mandelbrot et van Ness sur le "mouvement Brownien fractionnaire" (fractional Brownian motion, fBm).
-> Caractérisation une famille de processus stochastiques Gaussiens unidimensionnels VH(t) (H : réel compris entre 0 et 1, t : le temps).
Plus H est proche de 0 plus la courbe est bruitée. Une valeur de H égale à 0,5 quantifie une mouvement Brownien normal.
Autoaffinité:
(1) deux morceaux quelconques de la courbe représentative se ressembleront,
(2) si on effectue une mise à l'échelle d'un facteur r sur le temps et d'un facteur rH sur VH(t), la courbe garde toujours le même aspect.
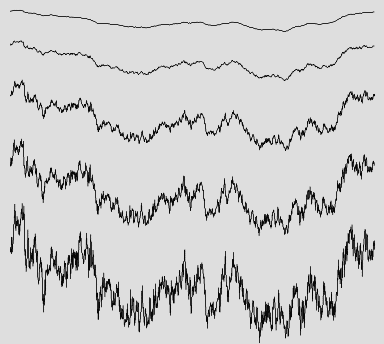
FBm avec des valeurs de H égales à 0.8, 0.6, 0.4, 0.3 et 0.2.
L'extension multidimensionnelle des fBm permet de modéliser un large éventail de phénomènes naturels.
Pour les reliefs, le paramètre temps t est transformé en un couple (x,y) indiquant une position dans le plan, VH(x,y) donne l'=itude du point P.
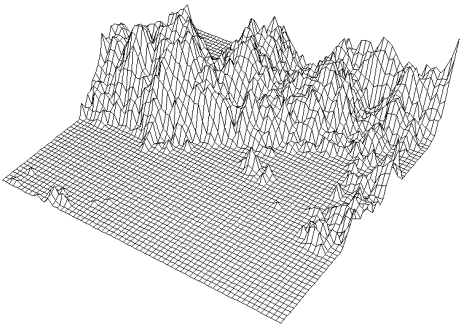
Un relief fractal généré par fBm représenté par facettes
Un objet fractal de dimension fractale D apparaît comme un fBm de coefficient H tel que D = E + 1 - H où E est le nombre de variables de la fonction fBm, c'est à dire la dimension euclidienne de l'objet construit.
Cet objet n'est évidemment pas strictement autosimilaire mais seulement autoaffine.
Implantation des fractales stochastiques
La programmation exacte des lois mathématiques requiert une quantité de calcul très importante.
Les implantations sont essentiellement des approximations du mouvement Brownien fractionnaire
soit par des techniques spatiales (subdivision récursive),
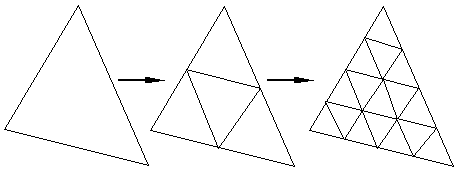
Fractalisation d'un triangle
soit par des techniques spectrales (par filtrage de Fourier).
Algorithmes
Fonctions de bibliothèque
/* ********************************* */
void initgauss(unsigned seed) {
nrand = 4 ;
arand = pow(2.,15.) - 1 ;
gaussadd = sqrt(3*nrand) ;
double val =(double)nrand*arand ;
gaussfac = 2*gaussadd/val ;
srand(seed) ;
}
/* ********************************* */
double rand_gauss(void) {
double sum ;
int i ;
for ( sum = 0,i = 0 ; i < nrand ; i++ )
sum += rand() ;
return(gaussfac*sum-gaussadd) ;
}
/* ********************************* */
FBm en dimension 1
#define MAXLEVEL 10
static unsigned arand,nrand ;
static double gaussadd,gaussfac ;
static double delta[MAXLEVEL+1] ;
/* ********************************* */
void midpointrecursion(double *x,
unsigned i0,
unsigned i2,
unsigned level,
unsigned maxlevel){
unsigned i1 ;
i1 = (i0+i2)/2 ;
x[i1] = 0.5*(x[i0]+x[i2])+
delta[level]*rand_gauss() ;
if ( level < maxlevel ) {
midpointrecursion(x,i0,i1,level+1,
maxlevel) ;
midpointrecursion(x,i1,i2,level+1,
maxlevel) ; }
}
/* ********************************* */
void midpointfm1D(double *x,
unsigned maxlevel,
double sigma,
double h,
unsigned seed) {
int i ;
unsigned n ;
initgauss(seed) ;
for ( i = 1 ; i <= maxlevel ; i++ )
delta[i] = sigma*pow(0.5,i*h)*
sqrt(1-pow(2.,2.*h-2.)) ;
n = 0x0001<<maxlevel ;
x[0] = 0 ;
x[n] = sigma * rand_gauss() ;
midpointrecursion(x,0,n,1,maxlevel) ;
}
/* ********************************* */
FBm en dimension 2
L'algorithme suivant génère un bruit fractal Brownien en dimension 2 par une méthode de subdivision récursive.
#define MAXLEVEL 10
unsigned arand,nrand ;
double gaussadd,gaussfac ;
double delta[MAXLEVEL+1] ;
/* ********************************* */
double f4(double delta,
double x0,
double x1,
double x2,
double x3) {
return((x0+x1+x2+x3)/4+delta*gauss()) ;
}
/* ********************************* */
double f3(double delta,
double x0,
double x1,
double x2) {
return((x0+x1+x2)/3+delta*gauss()) ;
}
/* ********************************* */
void midpointfm2D(double **x,
unsigned maxlevel,
double sigma,
double h,
unsigned addition,
unsigned seed) {
int d,dmaj,stage,xx,yy ;
unsigned n ;
double delta ;
initgauss(seed) ;
delta = sigma ;
n = 0x0001<<maxlevel ;
x[0][0] = delta * gauss() ;
x[0][n] = delta * gauss() ;
x[n][0] = delta * gauss() ;
x[n][n] = delta * gauss() ;
dmaj = n ;
d = n / 2 ;
for ( stage = 1 ;
stage <= maxlevel ;
stage++ ) {
delta *= pow(0.5,0.5*h) ;
for ( xx = d ; xx <= n-d ;
xx += dmaj )
for ( yy = d ; yy <= n-d ;
yy += dmaj )
x[xx][yy] = f4(delta,
x[xx+d][yy+d],
x[xx+d][yy-d],
x[xx-d][yy+d],
x[xx-d][yy-d]);
if ( addition )
for ( xx = 0 ; xx <= n ;
xx += dmaj )
for ( yy = 0 ; yy <= n ;
yy += dmaj )
x[xx][yy] += (delta*gauss()) ;
delta = delta * pow(0.5,0.5*h) ;
for ( xx = d ; xx <= n - d ;
xx += dmaj ) {
x[xx][0] = f3(delta,
x[xx+d][0],
x[xx-d][0],
x[xx][d]) ;
x[xx][n] = f3(delta,
x[xx+d][n],
x[xx-d][n],
x[xx][n-d]) ;
x[0][xx] = f3(delta,
x[0][xx+d],
x[0][xx-d],
x[d][xx]) ;
x[n][xx] = f3(delta,
x[n][xx+d],
x[n][xx-d],
x[n-d][xx]) ; }
for ( xx = d ; xx <= n-d ;
xx += dmaj )
for ( yy = dmaj ; yy <= n-d ;
yy += dmaj )
x[xx][yy] = f4(delta,
x[xx][yy+d],
x[xx][yy-d],
x[xx+d][yy],
x[xx-d][yy]) ;
for ( xx = dmaj ; xx <= n-d ;
xx += dmaj )
for ( yy = d ; yy <= n-d ;
yy += dmaj )
x[xx][yy] = f4(delta,
x[xx][yy+d],
x[xx][yy-d],
x[xx+d][yy],
x[xx-d][yy]) ;
if ( addition ) {
for ( xx = 0 ; xx <= n ;
xx += dmaj )
for ( yy = 0 ; yy <= n ;
yy += dmaj )
x[xx][yy] += delta*gauss() ;
for ( xx = d ; xx <= n-d ;
xx += dmaj )
for ( yy = d ; yy <= n-d ;
yy += dmaj )
x[xx][yy] += delta*gauss() ; }
dmaj /= 2 ;
d /= 2 ; }
}
/* ********************************* */
Les ensembles de Mandelbrot et de Julia-Fatou
Ces fractales sont issues de la même règle de calcul :
f : x -> x2 + c.
x et c sont des nombres complexes a + bi, x définit la position (a,b) dans le plan.
Rappel: si x = a + bi, alors x2 = a2 - b2 + 2abi.
Les carrés successifs d'un nombre complexe tendront vers 0 (respectivement l'infini, 1) pour les x initiaux de module inférieur à 1 (respectivement supérieur à 1, égal à 1).
Pour chaque position du plan, on applique itérativement la fonction f jusqu’à établir la convergence vers un nombre précis ou vers l’infini, ou bien établir la non convergence.
L’ensemble des points où la série converge vers 0 est l’ensemble de Julia-Fatou.
La forme de cet ensemble varie en fonction de la valeur de c.

Ensemble de Julia-Fatou pour x -> x2 - .9 + .12 i
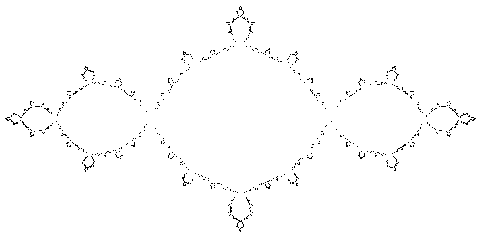
Bord de l'ensemble de Julia-Fatou pour x -> x2 - 1
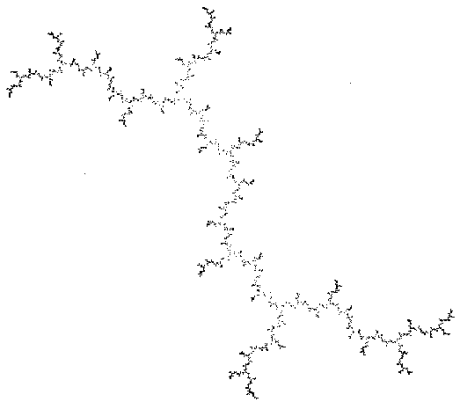
Ensemble de Julia-Fatou pour x -> x2 + i
Comme l'ensemble de Julia-Fatou, l’ensemble de Mandelbrot est issu de la fonction f : x -> x2 + c mais utilisée d’une manière différente.
Pour chaque valeur de c du plan, à partir de x = 0 + 0i, on applique un nombre fini de fois la fonction f, s’il y a convergence au bout du processus, le point fait partie de l’ensemble, sinon il n’en fait pas partie.
On obtient ainsi une image en noir et blanc.

Ensemble de Mandelbrot en noir et blanc
Une couleur est attribuée à chaque point du plan en fonction du nombre d’itérations qui ont été nécessaires pour établir la convergence ou la non convergence.
Le bord de l’ensemble est constitué de l’ensemble des points où la convergence n’a pas pu être formellement établie.

Ensemble de Mandelbrot en couleurs,
les zones de même couleur indiquent
les points où le nombre d’itérations
a été le même pour établir la convergence
ou la non convergence.
Conclusion
Les méthodes fractales sont considérées comme les plus efficaces pour la création d'images réalistes d'objets naturels.
Qualités:
Réalisme remarquable.
Très importante amplification des données (un très petit nombre de paramètres suffit à décrire un nuage ou une montagne fractale simple).
Niveau de détail aussi fin que voulu.
Les systèmes de fonctions itérées: I.F.S.
Définitions
IFS : Ensemble fini W de fonctions affines strictement contractantes {wn, 1<=n<=N} du plan.
Fonction affine du plan:
f(x,y) = (x',y') = (a1 x + b1 y + c1,a2 x + b2 y + c2)
On appelle "contractante" une fonction affine f telle que la distance d entre deux points p1 et P2 est plus grande que la distance entre f(p1) et f(p2).
Une fonction composition de mises à l’échelle (facteurs plus petit que 1), rotations et translations dans cet ordre est une fonction affine contractante.
L'"attracteur" de l'IFS (l'image obtenue par l'IFS) est l'unique point fixe A de W, ensemble limite des points itérés zn obtenus à partir d'un point z0 arbitraire du plan, en appliquant de façon itérée avec équiprobabilité les applications wi :
zn+1 = wi(zn).
Algorithme
n est le nombre de point tracés dans l'image.
Définir la position initiale Z au hasard Allumer pixel en position Z Pour i de 1 à n Choisir au hasard une fonction affine f Z <- f(Z) Allumer pixel en position Z Fin pour
Propriétés
Les IFS sont caractérisés par la très forte amplification des données qui contrôlent la forme d'une image:
6*N réels définissent les N transformations affines en deux dimensions.

Une feuille extraite du mémoire de DEA de Pascal Humbert (LIB, 1991). 2
IFS pour le limbe et le pétiole,
N = 10 fonctions affines -> 60 réels.
Les images obtenues sont fractales. Elles représentent souvent des objets à forte caractéristique autosimilaire (feuilles d'érable, fougères, sapins).
Problème inverse
Détermination d'un IFS ayant pour attracteur une image donnée.
Introduction de la notion d'auto-pavage :
On recouvre au mieux l'objet A avec un nombre minimum N de copies réduites de lui-même. A chacune de ces copies correspond une fonction affine de l'IFS.

IFS probabilisé
L'IFS est dit probabilisé si on munit d'une probabilité pi
(autre que ![]() ) la
transformation wi, 1 <= i <= N.
) la
transformation wi, 1 <= i <= N.
Conséquences:
Accélération de la vitesse de rendu en choisissant pi proportionnelle à l'aire wi(P) de l'image produite par wi.
Introduction de la couleur. Les points "tombent" avec différentes fréquences suivant les différents endroits donnant un "effet de trame" ou de couleur.
Exemples
Surface carrée uniforme
A1 = |
A2 = |
A3 = |
A4 = |
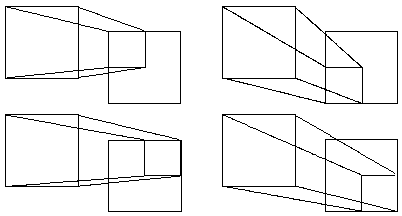

100000 itérations

500000 itérations
Surface carrée non-uniforme
A1 = |
A2 = |
A3 = |
A4 = |

Surface non-uniforme avec motifs
A1 = |
A2 = |
A3 = |
A4 = |


I.F.S. coloré
A1 = |
A2 = |
A3 = |
A4 = |

Chaque point allumé est tracé en noir.
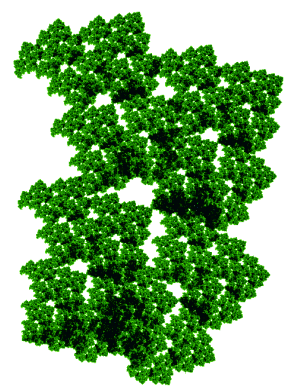
Les points sont d’autant plus noirs qu’ils ont été allumés souvent.
Applications
Synthèse d'images
Génération d'images 2D présentant les caractéristiques d'images 3D.
Compression d'images
Les temps de calcul sont très longs pour l'analyse de l'image.
Conclusion
Le caractère fractal des images obtenues permet d'obtenir des agrandissements à toute échelle tout en gardant le même code en mémoire et la même précision de rendu
-> compacité.
Le calcul itératif de l'image se poursuit jusqu'à l'obtention d'une image suffisamment consistante
-> choix possible de l'instant d'arrêt de l'algorithme.
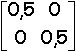 , B1 =
, B1 = 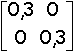 , B1 =
, B1 = 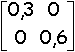 , B2 =
, B2 = 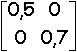 , B3 =
, B3 = 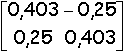 , B1 =
, B1 = 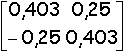 , B3 =
, B3 =