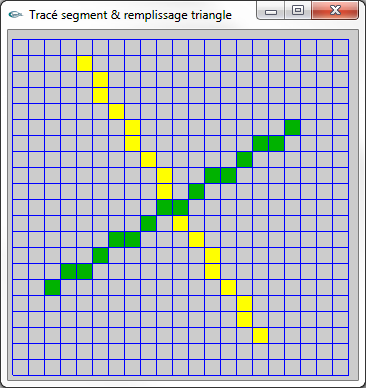
Figure (1) : Tracé des deux segments de droite
Commentaires
L'implantation de la fonction de tracé d'un segment de droite est la pure implantation de l'algorithme de Bresenham.
La fonction de rasterisation d'un triangle fait appel à la fonction auxiliaire cote destinée à
"rasteriser" un coté. Cette fonction n'a pas pour but de faire quelque dessin que ce soit, mais plutôt de déterminer une abscisse xmin
et une abscisse xmax pour chaque ordonnée y où il y a au moins un pixel sur le coté, ces abscisses étant destinées à servir d'abscisses extrêmes
initiale et finale pour chaque trame horizontale de pixels du triangle. Cette fonction prend en paramètres les coordonnées des pixels initiaux et
finaux du coté ainsi que les tableaux xmin et xmax destinés à recueillir les abscisses minimales et maximales. Les y peuvent directement
servir d'indices dans ce tableau. L'implantation de le fonction cote est basée en tout point
sur l'algorithme de Bresenham sauf qu'au lieu d'allumer des pixels, elle fait des écritures de valeurs d'abscisse dans xmin (resp.
xmax) aux indices y si des valeur trouvées par rasterisation sont plus petites (resp. plus grandes) que celles qui s'y trouvent.
La fonction triangle prend en paramètre, dans l'ordre, les coordonnées (x1,y1), (x2,y2) et (x3,y3)
des sommets P1, P2 et P3 définissant le triangle à rasteriser. Un point essentiel au bon fonctionnement de la fonction
triangle est que les 3 sommets P1, P2 et P3 doivent être triés par ordre d'ordonnées croissantes. La fonction
triangle débute par la déclaration des tableaux xmin et xmax destinés à recevoir les abscisses minimales et maximales
des trames horizontales de remplissage du triangle. Ces tableaux sont définis de taille 4096, autorisant une résolution en y de 4096 pixels comptée
des indices 0 (en bas) à 4095 (en haut). xmax est initialisé à 0. xmin est initialisé à une valeur plus grande que la plus grande valeur envisagée
pour une abscisse de pixel. Ensuite, elle procède à la rasterisation dans les tableaux xmin et xmax des cotés du triangle. Enfin, elle trace effectivement
les pixels en itérant sur y entre y1 et y3 inclus pour parcourir toutes les trames horizontales et, sur chaque trame, en itérant entre xmin[y] et
xmax[y] inclus pour allumer tous les pixels.
Remarque : Cette méthode de remplissage est bien adaptée au traitement de facettes triangulaires individuelles. Dans le cas où des ensembles de facettes adjacentes doivent être affichés. Les cotés partagés verront leurs pixels être affichés deux, une fois pour chaque facette. Il s'agit là d'une inoptimisation importante.

Figure (1) : Tracé des deux segments de droite
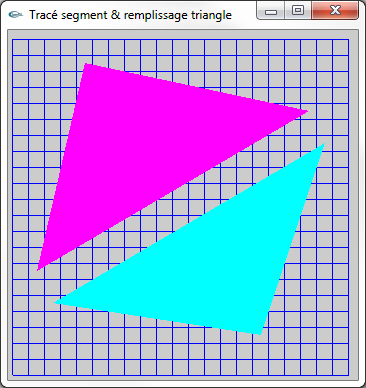
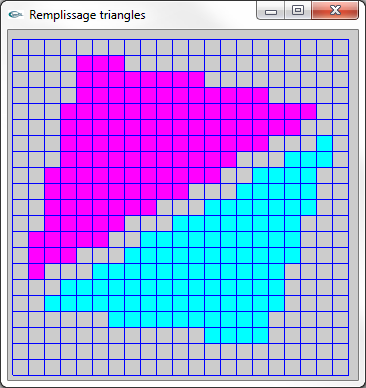
Figures (2) et (3) : Triangles rééls et rasterisés
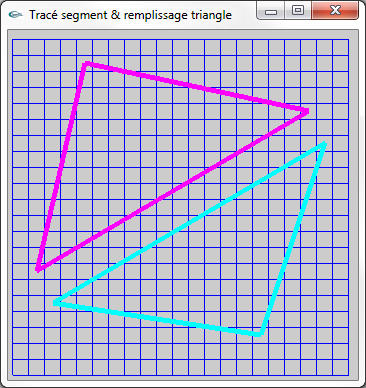

Figures (4) et (5) : Triangles dessinés par leurs cotés réels et rastérisés
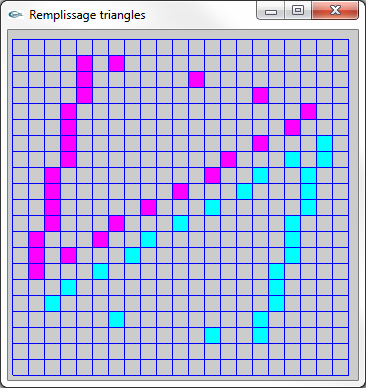
Figure (6) : Pixels extrèmes gauches et droits des trames horizontales des rectangles
-> derniers pixels sur la trame correspondant au bord dans le sens de son parcours de rasterisation

Figure (7) : Comparaison entre les pixels sélectionnés et les cotés rasterisés
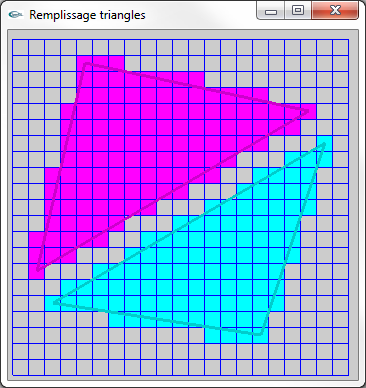
Figure (8) : Superposition des triangles réels dessinés par leurs bords et obtenus par rasterisation
Fichier source : RemplissageTriangle2D-2.cpp
/* Trace du segment de droite entre le pixel */
/* de coordonnees (xi,yi) et le pixel */
/* de coordonnees (xf,yf) au moyen de l'algorithme */
/* de Bresenham */
static void ligne(int xi,int yi,int xf,int yf) {
int x = xi;
int y = yi;
int dx = xf - xi;
int dy = yf - yi;
int xinc = ( dx > 0 ) ? 1 : -1;
int yinc = ( dy > 0 ) ? 1 : -1;
dx = abs(dx);
dy = abs(dy);
pixel(x,y);
if ( dx > dy ) {
int cumul = dx >> 1;
for ( int i = 1 ; i <= dx ; i++ ) {
x += xinc;
cumul += dy;
if ( cumul >= dx ) {
cumul -= dx;
y += yinc; }
pixel(x,y); } }
else {
int cumul = dy >> 1;
for ( int i = 1 ; i <= dy ; i++ ) {
y += yinc;
cumul += dx;
if ( cumul >= dy ) {
cumul -= dy;
x += xinc; }
pixel(x,y); } }
}
/* Rasterisation du cote de sommet initial (xi,yi) */
/* et de sommet final (xf,yf) en stockant */
/* dans le tableau px le dernier x */
/* calcule pour chaque y */
static void cote(int xi,int yi,int xf,int yf,int *px) {
int x = xi;
int y = yi;
int dx = xf - xi;
int dy = yf - yi;
int xinc = ( dx > 0 ) ? 1 : -1;
int yinc = ( dy > 0 ) ? 1 : -1;
dx = abs(dx);
dy = abs(dy);
px[y] = x;
if ( dx > dy ) {
int cumul = dx >> 1;
for ( int i = 1 ; i <= dx ; i++ ) {
x += xinc;
cumul += dy;
if ( cumul >= dx ) {
cumul -= dx;
y += yinc; }
px[y] = x; } }
else {
int cumul = dy >> 1;
for ( int i = 1 ; i <= dy ; i++ ) {
y += yinc;
cumul += dx;
if ( cumul >= dy ) {
cumul -= dy;
x += xinc; }
px[y] = x; } }
}
static void pixel(int x,int y,int *xmin,int *xmax) {
if ( x < xmin[y] )
xmin[y] = x;
if ( x > xmax[y] )
xmax[y] = x;
}
/* Rasterisation du cote de sommet initial (xi,yi) */
/* et de sommet final (xf,yf) en stockant */
/* dans le tableau px le dernier x */
/* calcule pour chaque y */
static void cote(int xi,int yi,int xf,int yf,int *xmin,int *xmax) {
int x = xi;
int y = yi;
int dx = xf - xi;
int dy = yf - yi;
int xinc = ( dx > 0 ) ? 1 : -1;
int yinc = ( dy > 0 ) ? 1 : -1;
dx = abs(dx);
dy = abs(dy);
pixel(x,y,xmin,xmax);
if ( dx > dy ) {
int cumul = dx >> 1;
for ( int i = 1 ; i <= dx ; i++ ) {
x += xinc;
cumul += dy;
if ( cumul >= dx ) {
cumul -= dx;
y += yinc; }
pixel(x,y,xmin,xmax); } }
else {
int cumul = dy >> 1;
for ( int i = 1 ; i <= dy ; i++ ) {
y += yinc;
cumul += dx;
if ( cumul >= dy ) {
cumul -= dy;
x += xinc; }
pixel(x,y,xmin,xmax); } }
}
/* Rasterisation d'un triangle 2D */
/* (x1,y1), (x2,y2) et (x3,y3) sont les coordonnees */
/* des trois sommets du triangle et doivent respecter */
/* y1 <= y2 <= y3 */
/* Solution imparfaite car ne gerant pas le probleme */
/* des cotes ou plus d'un pixel existe pour chaque y */
/* avec l'obligation de choisir un et un seul */
/* de ces pixels par y */
/* Consequences possibles : */
/* Non affichage sur les cotes de pixels qui auraient */
/* ete affiches si les cotes avaient ete rasterises */
/* par affichage de segments de droite rasterises. */
/* Apparition de trous entre deux facettes adjacentes */
/* car des pixels peuvent ne pas etre allumes */
/* a la limite entre les deux facettes car allumes */
/* pour aucune des deux facettes. */
static void triangle1(int x1,int y1,int x2,int y2,int x3,int y3) {
int xd[4096];
int xg[4096];
if ( (x2-x1)*(y3-y1)-(x3-x1)*(y2-y1) > 0 ) {
cote(x1,y1,x2,y2,xd);
cote(x2,y2,x3,y3,xd);
cote(x1,y1,x3,y3,xg); }
else {
cote(x1,y1,x2,y2,xg);
cote(x2,y2,x3,y3,xg);
cote(x1,y1,x3,y3,xd); }
for ( int y = y1 ; y <= y3 ; y++ ) {
for ( int x = xg[y] ; x <= xd[y] ; x++ ) {
pixel(x,y); } }
}
/* Rasterisation d'un triangle 2D */
/* (x1,y1), (x2,y2) et (x3,y3) sont les coordonnees */
/* des trois sommets du triangle et doivent respecter */
/* y1 <= y2 <= y3 */
static void triangle2(int x1,int y1,int x2,int y2,int x3,int y3) {
int xmin[4096];
int xmax[4096];
for ( int y = y1 ; y <= y3 ; y++ ) {
xmin[y] = 8192;
xmax[y] = -1; }
cote(x1,y1,x2,y2,xmin,xmax);
cote(x2,y2,x3,y3,xmin,xmax);
cote(x1,y1,x3,y3,xmin,xmax);
for ( int y = y1 ; y <= y3 ; y++ ) {
for ( int x = xmin[y] ; x <= xmax[y] ; x++ ) {
pixel(x,y); } }
}