Sujets et Corrections
de TD et TP
![]()
|
Fichier zip |
TP n°1 : Premières implantations OpenGL
Exercice n°1
Télécharger le fichier archive IG-2019-2020.zip. Ce fichier archive contient une "solution" Visual Studio
2015.
Après extraction, un répertoire IG-2019-2020 est créé. Ce répertoire contient lui-même 6 répertoires:
- Bin pour les exécutables,
- Include pour les fichiers d'entête OpenGL (fichiers non présents dans Visual Studio),
- Lib pour les fichiers librairie OpenGL (fichiers non présents dans Visual Studio),
- Projet pour le fichier de description de la solution (Projet.sln) et les répertoires contenant les projets faisant partie de la solution
(Un seul répertoire actuellement: Exemple),
- Src pour les fichiers source des projets inclus dans la solution,
- Temp pour les fichiers temporaires (solution, compilation, ...).
La solution comprend un seul projet nommé Exemple. Ce projet référence un seul fichier source Exemple.cpp et est configuré pour une compilation utilisant
OpenGL:
- fichiers d'entête (répertoire implicite ../../Include),
- fichiers librairie: OpenGL32.ms.lib et glu32.ms.lib dans les options de configuration GUI et glut32.ms.lib par référence directe,
- copie dans le répertoire Bin de l'exécutable généré dans un sous-répertoire du répertoire Temp.
La compilation (génération) de ce projet doit conduire à la création d'un exécutable nommé Exemple.exe dans le répertoire Bin. Son exécution
requière les dll OpenGL32.dll et Glu32.dll (toujours présentes par défaut dans le système d'exploitation Windows) ainsi que la dll Glut32.dll
(jamais présente par défaut dans le système d'exploitation Windows mais dont il existe une copie dans le répertoire Bin où est copié l'exécutable).
1) Extraire l'archive IG-2019-2020.zip. Lancer Visual Studio 2015 et charger la solution. Vérifier la compilation et l'exécution du projet Exemple.
Le fichier code source GLUtMinimum.cpp illustre le fonctionnement événementiel de la librairie GLUt. On rappelle que nous allons utiliser cette librairie annexe à OpenGL pour construire l'interface utilisateur de nos programmes OpenGL, celui-ci ne contenant aucune fonction dédiée à cette fin.

Le fichier source GLUtMinimum.cpp contient le minimum d'appels à OpenGL de façon à mettre en évidence
les fonctionnalités GLUt et non les fonctionnalités OpenGL. La scène construite est constituée d'un unique tore. Le calcul d'illumination
est activé et une seule lumière est allumée. L'élimination des parties cachées est activée. La projection est réalisée en projection orthographique.
Le contenu du volume cubique dont la diagonale est définie par les positions (-1.0,-1.0,-1.0) et (1.0,1.0,1.0) du repère de modélisation est affiché
dans le viewport de visualisation en projection selon l'axe -z du repère de modélisation. Le viewport de visualisation est configuré pour occuper
automatiquement (dynamiquement) l'intégralité de la fenêtre.
La fonction main organise les points suivants:
- exécution d'une fonction (static void clean(void)) lorsque l'application est interrompue par exécution de la fonction exit,
- configuration et création de la fenêtre de visualisation,
- configuration des paramètres OpenGL qui doivent l'être et qui n'auront pas à être reconfigurés au cours de la vie du programme,
- programmation de la gestion des événements,
- affichage de la fenêtre de visualisation et lancement de la boucle infini de gestion des événements.
Les événements suivants sont gérés "normalement" avec exécution de code OpenGL:
- rafraichissement de la fenêtre de dessin (display),
- modification de la taille de la fenêtre de dessin (reshape).
Les événements suivants sont gérés a minima par affichages écran texte de façon à permettre la trace du fonctionnement du programme par messages
dans la fenêtre console:
- frappe d'une touche alphanumérique du clavier (keyboard),
- frappe d'une touche non-alphanumérique du clavier (special),
- clic souris dans la fenêtre de dessin (mouse),
- déplacement de la souris bouton appuyé dans la fenêtre de dessin (mouseMotion).
Le code de gestion des événements suivants est programmé pour une gestion a minima par affichages écran texte, mais ces événements ne sont pas activés
(lignes laissées en commentaire) dans la fonction main:
- aucun événement n'est en attente (idle),
- déplacement de la souris bouton non appuyé devant la fenêtre de dessin (passiveMouseMotion).
Le fichier GLUt-3-spec.pdf contient la documentation de référence de GLUt. Il pourra vous aider à implanter les réponses aux questions suivantes.
2) Télécharger et remplacer le fichier Exemple.cpp par le fichier GLUtMinimum.cpp dans le projet VisualStudio.
Précision liminaire : La programmation GLUt ne peut être réalisée sans utiliser des variables globales. Celles-ci permettent le partage d'informations entre les différentes fonctions implantée pour être exécutées en réponse aux événements.
a) Implanter un contrôle clavier permettant de switcher entre les modes d'affichage plein et fil de fer en utilisant la touche de clavier Espace. Il convient de modifier la fonction keyboard et d'utiliser la fonction glPolygonMode.
b) Implanter une animation telle que le tore tourne sur lui-même autour de l'axe Ox à raison de 1° de rotation entre chaque image. Il convient d'adpater la fonction idle et de programmer son exécution en tâche de fond. La fonction glRotatef est utilisée dans la fonction display pour réaliser la rotation.
c) Implanter un contrôle clavier permettant d'activer/désactiver l'animation au moyen de la touche Entrée. On s'inspirera de la méthode utilisée dans Exemple.cpp.
d) Implanter un contrôle clavier permettant de faire tourner le tore sur lui-même autour de l'axe Oy dans un sens ou dans l'autre en utilisant les touches Flèche gauche et Flèche droite. Il convient d'adapter la fonction "special".
e) Implanter un contrôle permettant de faire tourner le tore sur lui-même autour de l'axe Oz en réaction aux mouvements horizontaux de la souris à raison de 1° de rotation par pixel de déplacement. Il convient d'adapter les fonctions mouse et mouseMotion.
|
GLUT |
||
|
Fonctionnalités principales de GLUt: - création de fenêtres - gestion des événements : - fenêtre, - clavier, - souris |
||
![]()
TD n°1 : Premières scènes OpenGL
Exercice n°1
(1) Programmer en OpenGL la scène suivante sous la forme d'une fonction C sans utiliser les fonctions glPushMatrix et glPopMatrix ailleurs
qu'en début et fin de fonction:
Quatre cubes de coté 2.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
(2) Reprogrammer en OpenGL la scène de la question (1) de telle manière que les cubes aient une de leurs faces orientée vers l'origine du repère.
(3) Reprogrammer en OpenGL la scène de la question (2) en utilisant les fonctions glPushMatrix et glPopMatrix pour rendre les objets indépendants les uns des autres et simplifier l'écriture de la fonction scène.


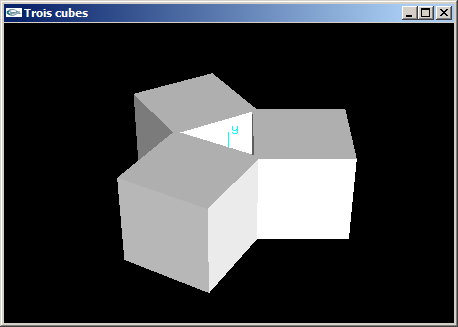
(4) Programmer une scène OpenGL en plaçant 3 cubes de coté 2.0 aux 3 sommets d'un triangle équilatéral défini
avec les caractéristiques suivantes:
- rayon 1.5,
- centré sur l'origine,
- plongé dans le plan xOz.
Les 3 cubes présentent une de leurs faces orientée vers l'origine.

Exercice n°2
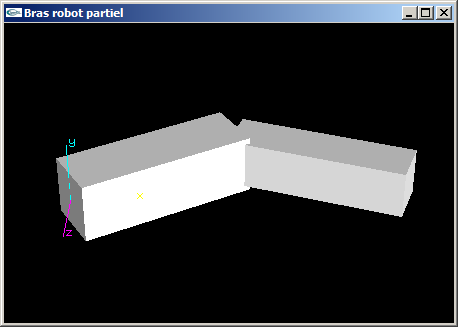
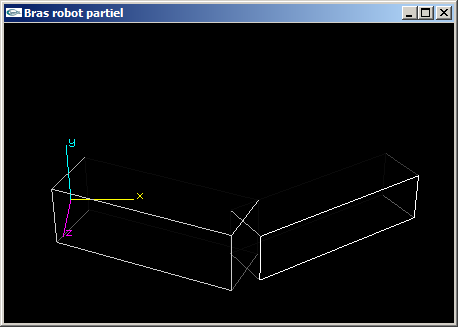
(1) Programmer la scène OpenGL modélisant un bras robot simplifié composé d'un bras et d'un avant-bras.
Le bras est articulé pour que sa base puisse tourner autour de l'axe Oy d'un angle r1. Il s'agit d'un parallélépipède
rectangle de dimension (3.0,1.0,1.0).
L'avant-bras est articulé autour de l'axe y au bout du bras pour un angle r2. Il s'agit d'un parallélépipède
rectangle de dimension (3.0,0.8,0.8).
(2) Modifier la fonction OpenGL de l'exercice n°1 en remplaçant les parallélépipèdes par des cylindres de tailles équivalentes à celles des objets qu'ils remplacent.
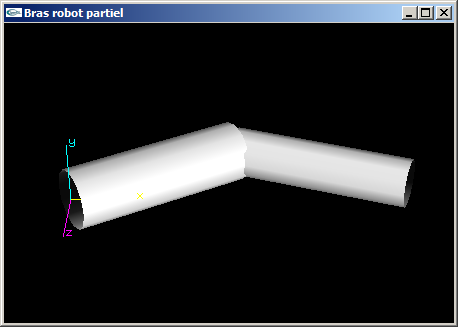
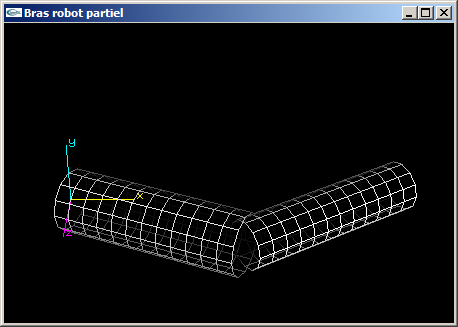
Exercice n°3 (supplémentaire)
(1) Implanter en OpenGL une fonction de dessin d'une molécule de Benzène (C6H6).
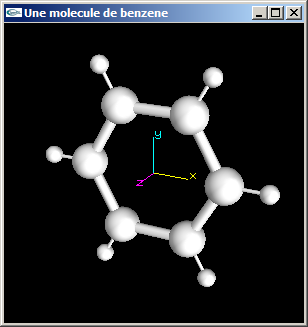
Les atomes de carbone (atomes centraux) ont un rayon égal à 0.5.
Les liaisons entre 2 atomes de carbone ont pour longueur (centre à centre) 2.0 et pour rayon 0.15.
Les atomes d'hydrogène ont un rayon égal à 0.25.
Les liaisons entre atome de carbone et d'hydrogène ont pour longueur (centre à centre) 1.2 et pour rayon 0.05.
La molécule est centrée sur l'origine et placée dans le plan xOy.
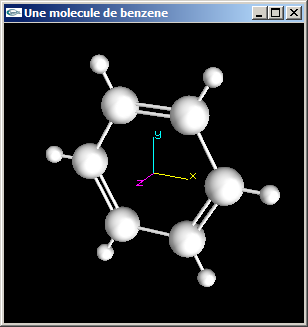
(2) Modifier la modélisation de la molécule de benzène de la question précédente pour que les liaisons carbone-carbone
soient alternativement des liaisons simples et des liaisons doubles (voir figure ci-dessous).
Les cylindres modélisant ces liaisons auront pour rayon 0.05 (comme les liaisons carbone-hydrogène). Dans le cas des liaisons doubles,
les deux cylindres de modélisation seront écartés de 0.1.
Solutions
| Quatre cubes (Question 3) |
| Trois cubes |
| Bras robot avec parallélépipèdes |
| Bras robot avec cylindres |
| Molécule de benzène |
TD n°2 : Modélisation par facettes
Exercice n°1
Modéliser par facettes une facette carrée percée d'un trou carré. Cette facette est plongée dans le plan xOy, centrée sur l'origine du repère de modélisation, de cotés parallèles aux axes x et y et de cotés de longueur 2.0. Le trou est centré sur l'origine du repère de modélisation, de cotés parallèles aux axes x et y et de cotés de longueur 1.0.

Exercice n°2
(1) Modéliser par facettes un cube de coté c centré sur l'origine du repère de modélisation. On ne générera
pas les normales.
La fonction créée aura pour prototype:
void mySolidCube(double c);
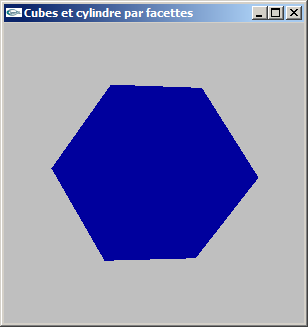
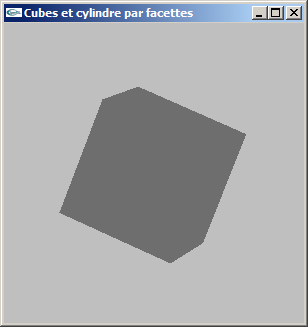
(2) Modifier la modélisation de la question précédente pour ajouter la gestion des normales.
Le but est de rendre possible les calculs d'éclairage.
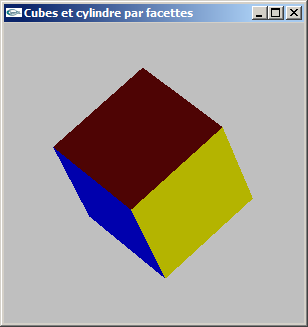
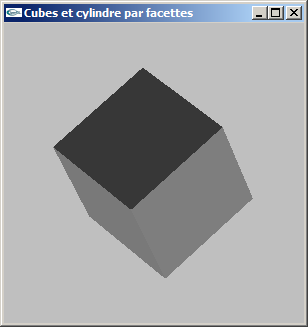
Exercice n°3 (supplémentaire)
Modéliser par facettes un cylindre selon les caractéristiques suivantes:
- choix du rayon,
- choix de la hauteur,
- choix du nombre de facettes en découpage longitudinal pour une valeur entière ns,
- centré sur l'origine du repère de modélisation,
- axé selon y.
On ne modélisera pas les bases du cylindre, mais uniquement le tube.
La fonction créée aura pour prototype:
void mySolidCylindre(double hauteur, double rayon, int ns);
Question supplémentaire: Ajouter un découpage latéral (selon l'axe y) pour une valeur nl.
Le prototype de la fonction devient:
void mySolidCylindre(double hauteur, double rayon, int ns, int nl);
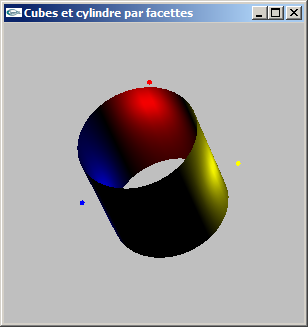
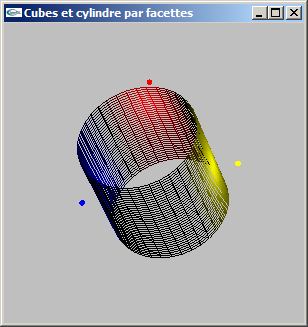
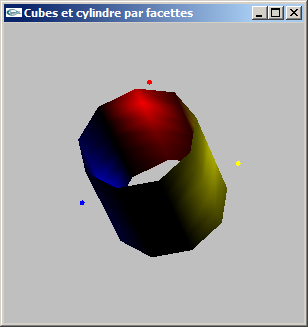
Solutions
TP n°3 : Modélisation par facettes et modélisation par objets géométriques
Exercice n°1
Implanter la fonction de modélisation par facettes d'un cube vue au TD n°1-2.
Exercice n°2
Implanter la scéne constituée de 4 cubes à faces orientées vers l'origine vue au TD n°1-2.
Implanter la scéne constituée d'un bras robot simplifié vue au TD n°1-2. On munira le programme de contrôles clavier permettant de faire varier les angles r1 et r2.
Exercice n°3
Récupérer la fonction de modélisation de cylindre par facettes proposées lors du TD n°1-2 et transformer les parallélipipèdes du bras robot par des cylindres.
Munir d'une pince le bras robot (modélisation libre, exemple ci-dessous).
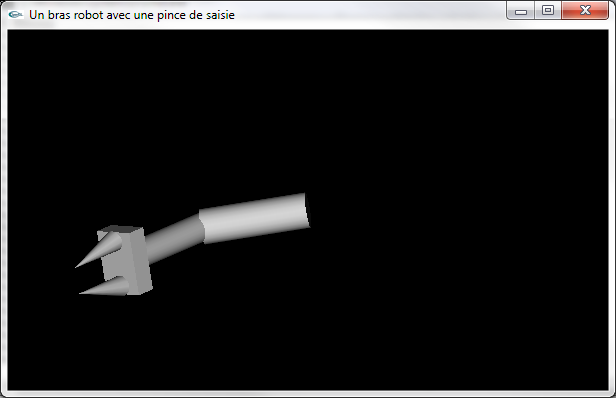
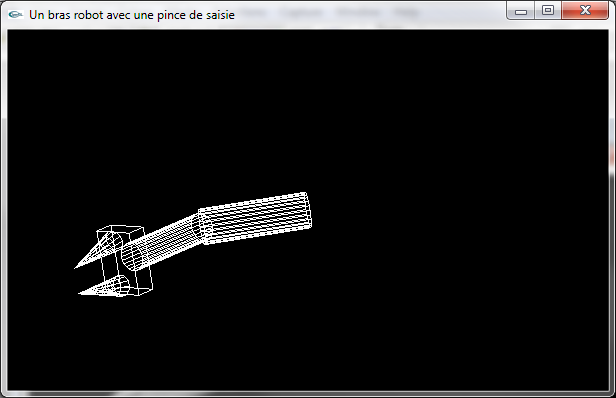
Modélisation d'une pince au bout du bras robot :
une embase pouvant tourner autour de l'axe de l'avant bras,
des mandibules coniques (fonction glutSolidCone) pouvant se déplacer par translation
![]()
TD n°3 : Paramètrage numérique de caméras
a) On considère une caméra de visualisation en projection parallèle orthographique placée en position (0.0, 0.0, 0.0) orientée selon l'axe (0.0,
0.0, -1.0). On considère une scène centrée sur le point de coordonnées (0.0, 0.0, -100.0) et occupant un volume sphérique de rayon 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans une fenêtre d'affichage carrée (viewport carré)?
Définir le paramétrage numérique de la fonction OpenGL utilisée pour réaliser cette visualisation: glOrtho.
b) On considère une caméra de visualisation en projection en perspective placée en position (0.0, 0.0, 0.0) orientée selon l'axe (0.0, 0.0, -1.0).
On considère une scène centrée sur le point de coordonnées (0.0, 0.0, -100.0) et occupant un volume sphérique de rayon 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans une fenêtre d'affichage carrée (viewport carré)?
Définir le paramétrage numérique de la fonction OpenGL utilisée pour réaliser cette visualisation: gluPerspective.
c) Dans le cadre d'une implantation OpenGL, décrire une solution permettant de s'assurer que l'intégralité de la scène sera visualisée quel que soit le ratio résolution horizontale sur résolution verticale adopté par le viewport d'affichage.
Solutions
![]()
TP n°4 : Caméras virtuelles
Le fichier code source ParametrageCamera.cpp contient un programme C+OpenGL complet réalisant
la modélisation géométrique d'une scène et organisant son affichage écran. Cette scène est constituée de 64 cubes de coté 0.5 placés en 4 plans
de 4x4 cubes de façon à occuper un volume cubique de coté 6.5 centré sur l'origine du repère de modélisation. Les cubes sont colorés en fonction
de leur position dans la scène (de plus en plus rouge de gauche à droite, de plus en plus vert de bas en haut, de plus en plus bleu de l'arrière
vers l'avant). L'affichage est réalisé en projection parallèle orthographique de façon à ce que l'intégralité de la zone d'affichage
de la fenêtre soit utilisée pour le viewport OpenGL. On rappelle que la direction de visualisation est la direction -z.
Télécharger et compiler ce fichier. Vérifier la bonne exécution de l'exécutable ainsi obtenu.
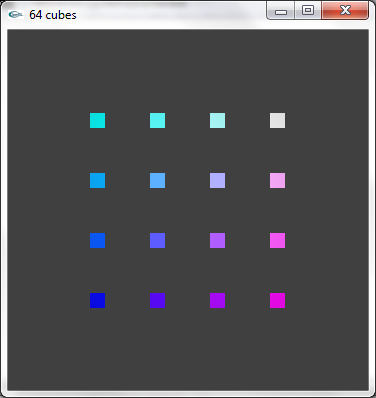
a) Lorsque la fenêtre de visualisation est modifiée par l'utilisateur pour adopter une résolution en x différente de la résolution en y, les objets affichés sont déformés.
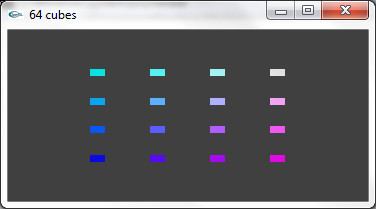

Résoudre ce problème de façon que cette déformation disparaisse et que la scène reste intégralement visible quel que soit le ratio résolution en x / résolution en y.


b) Modifier le code source pour que l'affichage ne soit plus réalisé en projection parallèle orthographique mais en projection en perspective.
On placera la caméra virtuelle en position (0.0,0.0,100.0). On l'orientera de façon qu'elle regarde l'origine du repère de modélisation
(sur laquelle la scène est centrée). On choisira la direction y comme direction de la verticale.
Il convient ici d'utiliser la fonction gluPerspective à la place de la fonction glOrtho (dans la fonction reshape) et d'ajouter un appel
à la fonction gluLookAt dans la fonction display en plaçant cet appel juste avant l'appel à la fonction scene de façon que les coordonnées spécifiées
en paramètres de gluLookAt soient considérées dans le même repère que celui associé à la scène, à savoir le repère de modélisation. On choisira les
paramètres d'appel du gluPerspective et du gluLookAt de façon réfléchie (autant que possible pas d'essai "pour voir"). Rappel :
Les paramètres d'appel de ces deux fonctions sont généralement liés.
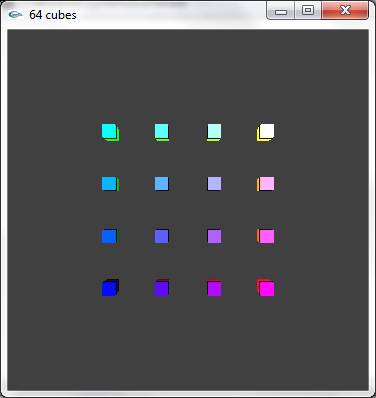
c) Modifier une nouvelle fois le code source pour que la caméra virtuelle soit maintenant placée en position (0.0,0.0,10.0).

d) Modifier une dernière fois le code source pour qu'il soit possible de contrôler la position de la caméra en utilisant le clavier:
- Up et Down pour la déplacer en y,
- Right et Left pour la déplacer en x,
- Page up et Page down pour la déplacer en z.
Elle reste orientée vers l'origine du repère de modélisation.

Question supplémentaire: On a placé l'appel à gluLookAt entre les appels aux fonctions glLightfv et scene. Déplacer l'appel à gluLookAt juste avant l'appel à glLightfv et tester le programme ainsi obtenu. La scène affichée est géométriquement identique mais les couleurs issus des calculs d'éclairage sont différents. Pourquoi?
Solutions
|
GLUT |
||
| Parametrage d'une caméra OpenGL (a) | ||
| Parametrage d'une caméra OpenGL (b) | ||
| Parametrage d'une caméra OpenGL (c) | ||
| Parametrage d'une caméra OpenGL (d) | ||
![]()
TP n°5 : Lumières et matériaux
Le fichier source LumieresEtMaterielBase.cpp implante un programme d'affichage OpenGL
dans lequel, à l'exception d'une, toutes les instructions spécifiques à la gestion des matériaux et des lumières ont été omises. L'instruction
conservée se trouve dans la fonction init. Elle a pour but de supprimer (configurer à noir) la lumière ambiante existant par défaut au sein d'OpenGL
(configurée par défaut à (0.2,0.2,0.2,1.0)) en plus des lumières classiques (GL_LIGHT0 à GL_LIGHT7).
Ce programme implante la modélisation géométrique de deux scènes. La première est composée de 3 tores. La seconde ne comporte qu'un cube. On
notera toutefois que, dans le but d'améliorer les calculs d'illumination, le cube est modélisé de façon à intégrer la décomposition de chacune
de ses 6 faces en un maillage de 100x100 facettes élémentaires carrées. La touche 's' permet de switcher entre les deux scènes. La touche
Espace permet de switcher entre les modes d'affichage plein et fil de fer.
Ce programme implante une fonctionnalité d'animation de la scène par rotation autour d'elle-même. Cette animation peut être activée/désactivé
au moyen de la touche 'a'. La touche F2 permet de ramener la scène à sa configuration de rotation initiale.
Ce programme intègre des appels à des fonctions actuellement vides destinées à isoler les portions de code OpenGL dédiées à la configuration des
lumières et des matériaux utilisés :
- static void configurationLumieres(void) : configuration des lumières,
- static void configurationMaterielTore1(void) : configuration du matériel du premier tore,
- static void configurationMaterielTore2(void) : configuration du matériel du deuxième tore,
- static void configurationMaterielTore3(void) : configuration du matériel du troisième tore,
- static void configurationMaterielCube(void) : configuration du matériel du cube.
A noter : Dans la fonction display, les fonctions OpenGL glPushAttrib et glPopAttrib sont utilisées pour sauvegarder dans une pile ad hoc et restaurer de façon rapide l'intégralité de la configuration des lumières et du matériel. Le paramètre de glPushAttrib dédié à cette sauvegarde est GL_LIGHTING_BIT.




Le but du TP consiste à placer les instructions de configuration des calculs d'illumination dans le respect des questions posées.
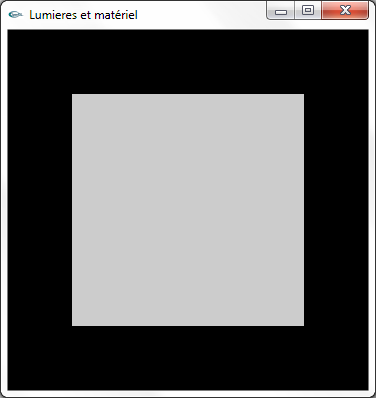
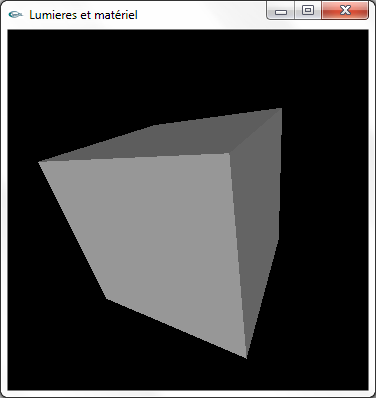
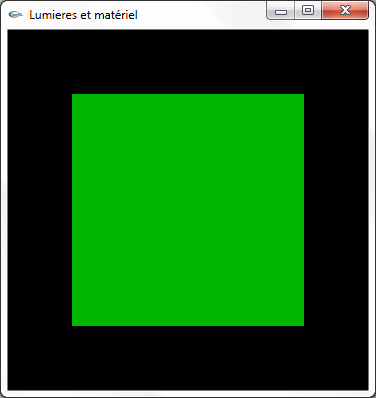
a) Activer l'utilisation des calculs d'éclairage.


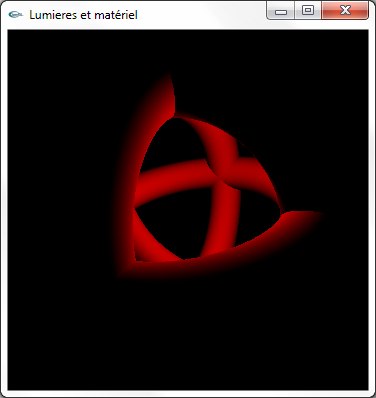
b) Activer et configurer la lumière 0 selon les caractéristiques suivantes:
- Lumière ponctuelle placée en position (2.0,2.0,2.0)
- Emission diffuse rouge
- Pas d'émission spéculaire
- Pas d'émission ambiante



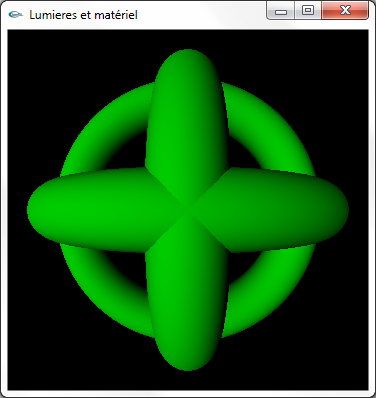
c) Désactiver la lumière 0. Activer et configurer la lumière 1 selon les caractéristiques suivantes:
- Lumière directionnelle de direction d'incidence (-2.0,0.0,4.0)
- Emission diffuse verte
- Emission spéculaire blanche
- Pas d'émission ambiante


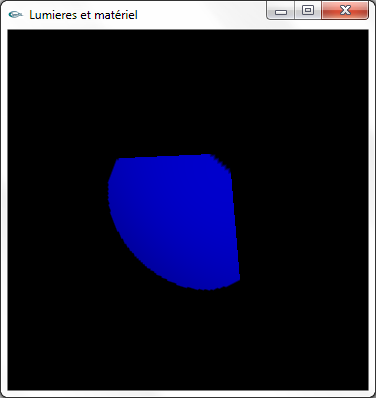
d) Désactiver la lumière 1. Activer et configurer la lumière 2 selon les caractéristiques suivantes:
- Spot placé en position (-2.0,-2.0, 10.0) et de direction d'éclairage (3.0, 3.0,-10.0)
- Spot d'ouverture globale égale à 40°
- Emission diffuse bleue
- Emission spéculaire jaune
- Pas d'émission ambiante



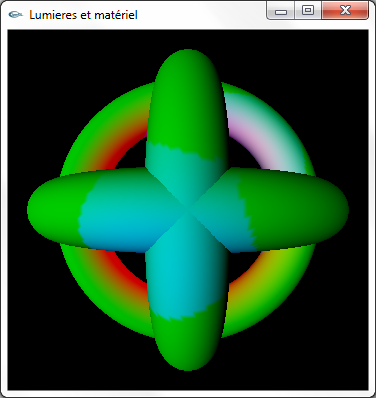
e) Activer simultanément les lumières 0, 1 et 2.

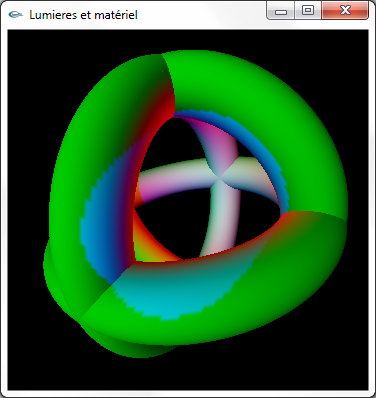
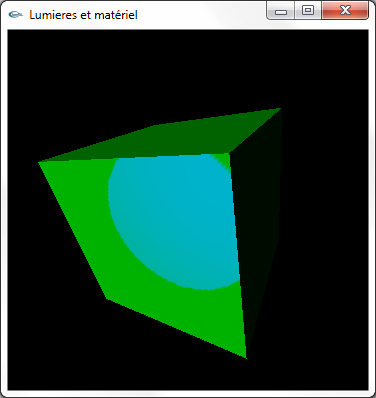
f) On aura remarqué que les émissions spéculaires des questions (c) et (d) semblent ne pas produire de résultat à l'écran. Ceci s'explique
par le fait que le matériel par défaut d'OpenGL ne génère pas de réponse à ce type d'éclairage.
Configurer le matériel des tores et du cube pour qu'il génère une réponse spéculaire blanche avec une réflectivité de 64.0 (valeur intermédiaire
entre les valeurs générant les réponses maximales et minimales : 0.0 et 128.0).
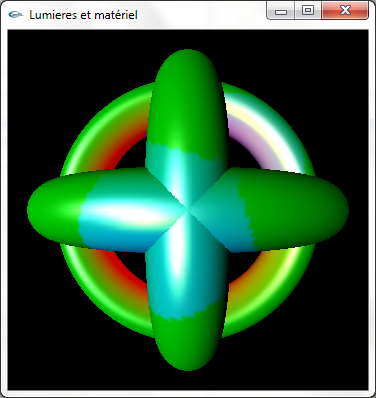

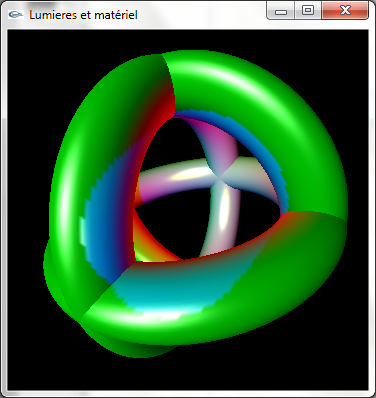

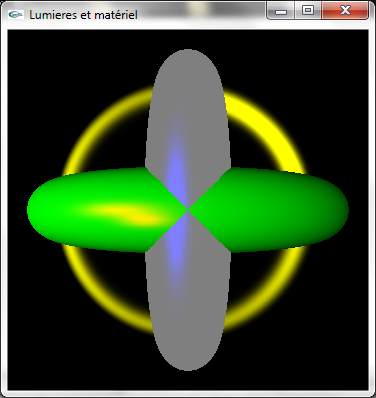
g) Modifier le matériel des tores selon les caractéristiques suivantes:
- Tore n°1: pas de réflexion diffuse, réflexion spéculaire jaune, réflectivité de 15.0, pas de réflexion ambiante, pas d'émission
- Tore n°2: réflexion diffuse jaune, réflexion spéculaire rouge, réflectivité de 100.0, pas de réflexion ambiante, pas d'émission
- Tore n°3: réflexion diffuse rouge, réflexion spéculaire bleue, réflectivité de 64.0, pas de réflexion ambiante, émission grise (gris moyen)
Questions optionnelles
1) Tester la possibilité offerte par OpenGL de créer des lumières ponctuelle ou spot intégrant une atténuation de l'éclairage fonction de la
distance entre la lumière et le point qu'elle éclaire : atténuation linéaire, atténuation quadratique.
Rappel : par défaut, il n'y a pas d'atténuation pour ces deux types de lumières.
2) Réaliser une animation où les lumières tournent autour de l'origine et la scène reste immobile.
3) Tester l'influence du nombre de facettes de modélisation sur les éclairages et la vitesse d'animation.
4) Tester l'utilisation de valeurs supérieures à 1.0 pour les coefficients des "couleurs" pour les lumières et les matériels.
Rappel : Utiliser des coefficients numériques supérieurs à 1.0 est tout à fait admis pour les lumières (notion d'énergie). Ce n'est pas le
cas pour les matériels.
Solutions
|
GLUT |
||
| Lumières et matériel | ||
TP n°6 : Plaçage de texture
L'archive zip ChargementImagePNG.zip contient les fichiers "code source" d'une librairie de gestion de fichiers "image" au format png accompagnés d'un exemple d'utilisation sous la forme d'une fonction main tentant deux chargements d'image successifs : Inconnu.png (qui n'existe pas) et Emojis.png (qui existe).

Plus précisément, une fonction d'importation et une fonction d'exportation sont décrites dans le fichier
ChargePngFile.h.
La fonction d'importation prend en paramètre le nom du fichier png à importer et deux pointeurs sur entier destinés à récupérer la résolution
en x et la résolution en y de l'image importée. Elle retourne un pointeur sur unsigned char correspondant au tableau d'octets issu de l'importation
(NULL si échec). Le tableau retourné est alloué dynamiquement par malloc et se doit d'être libéré par free après utilisation. Il contient les
composantes RVB des pixels codées sur 8 bits (1 octet) et entrelacées dans l'ordre rouge, vert, bleu si le fichier image importé était un fichier
au format png 24 bits entrelacé.
a) Télécharger et désarchiver ce fichier zip.
- Windows : Ouvrir la solution Visual Studio accompagnant les fichiers sources. Compiler, exécuter et vérifier la bonne exécution de l'exécutable
obtenu.
- Linux : Ne conserver que le fichiers sources c, cpp et h dans leurs répertoires respectifs ainsi que le fichier Emojis.png présent dans
le répertoire bin. Au moyen du gestionnaire de projet de développement que vous avez l'habitude d'utiliser, créer un projet incluant l'ensemble
des fichiers c et cpp fournis et générant l'exécutable dans le répertoire bin. Compiler, exécuter et vérifier la bonne exécution de l'exécutable
obtenu.
b) Développer un programme OpenGL permettant d'afficher une scéne composée d'un rectangle de coté 7.5 x 5.0. On pourra utiliser comme base le code développé au cours du TP n°4.

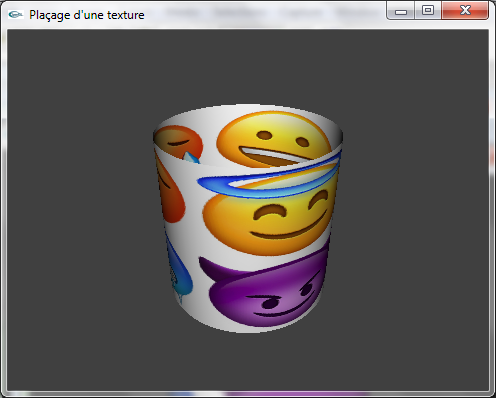
c) Modifier le code source de la question (b) pour que le rectangle soit muni d'une texture le recouvrant entièrement utilisant l'image contenue dans le fichier Emojis.png.
d) Reprendre la fonction de modélisation de cylindre de l'exercice n°2 du TD n°3 pour y ajouter les instructions permettant de le recouvrir d'une texture. Dans le programme de la question (c), remplacer le rectangle par un cylindre de hauteur 5.0 et de rayon 2.5.
Solutions
|
GLUT |
||
| Plaçage de texture | ||
Utiliser plusieurs textures
Les programmes ci-dessous montrent l'utilisation de plusieurs textures pour dessiner un cube où chacune des 6 faces est texturée au moyen d'une
image différente de celles des 5 autres faces.
Le premier programme est une simple adaptation du programme de la question (c). Le second programme montre comment installer les textures en mémoire
de la carte graphique au cours d'une première phase pour ensuite les utiliser à la demande de façon rapide au cours de la phase de modélisation
du cube.

|
GLUT |
||
| Plaçage de textures multiples (chargement à la demande) | ||
| Plaçage de textures multiples (chargement préalable) | ||
![]()
TD n°5 : Coordonnées homogènes et test de planarité
Exercice n°1
Proposer une méthode permettant de tester la planarité d'une facette non dégénérée à 4 sommets.
Exercice n°2
a) Développer en C++ une classe coordonnees homogenes 3D nommée CH3D.
b) Dériver de la classe CH3D une classe position 3D nommée Pos3D utilisable pour le stockage de positions dans un espace à trois dimensions.
c) Dériver de la classe CH3D une classe direction 3D nommée Dir3D utilisable pour le stockage de directions dans un espace à trois dimensions.
d) Développer une méthode de calcul du produit scalaire de deux Dir3D.
e) Développer une méthode de calcul du produit vectoriel de deux Dir3D.
f) Implanter une fonction ou une méthode de test de la planarité de facettes à 4 sommets.

Solutions
![]()
TP n°7 : Lancement du projet
Description du travail à réaliser
De façon à faciliter le développement du projet, réaliser le test des deux fichiers sources suivants:
- DeuxFenetres.cpp
- TestMemoire.cpp
Le fichier DeuxFenetres.cpp illustre la possibilité offerte par GLUt de gérer plusieurs fenêtres d'affichage OpenGL. La fonction int glutCreateWindow(void) permet de créer les fenêtres. Elle retourne un handle entier à mémoriser permettant de garder une référence sur chaque fenêtre ouverte. Les fenêtres sont individuellement munies de leurs fonctions display, reshape, keyboard, special, mouse, ... qui permettent de gérer leur fonctionnement événementiel. Attention, les fenêtres partagent une et une seule fonction idle. Chaque fenêtre peut recevoir en propre un ordre de rafraichissement en utilisant la fonction void glutPostWindowRedisplay(int f) où f est le handle de la fenêtre à rafraîchir. Dans chaque fenêtre est géré un environnement OpenGL complet pouvant/devant être intégralement paramétré : lumières, matériaux, textures, caméra, options d'affichage, ...
Le fichier TestMemoire.cpp montre une technique spécifique à VisualStudio permettant de contrôler les opérations de gestion dynamique de la mémoire
: new, delete, calloc, malloc, free,... Le but de cette technique est de faciliter la détection des problèmes souvent constatés quant à la gestion
dynamique de la mémoire : free ou delete dupliqué, pas de free pour un alloc, pas de delete pour un new, ... Il s'agit d'un équivalent à
valgrind. Attention, les bibliothèques de compatibilté mfc doivent être installées (option non activée par défaut au moment de l'installation
de VisualStudio) pour que TestMemoire.cpp puisse être compilé et donc exécuté.
Pour que le contrôle soit réalisé, il est nécessaire que la compilation soit réalisée en mode "Debug" et que l'exécution soit lancée
sous debugger. Les directives de compilation incluses dans le code source font que la compilation et l'exécution sont possibles sans problème
en mode release ou bien si un autre compilateur que VisualStudio est utilisé. Le code est instrumenté au début avec un certain nombre de #include
et dans la fonction main avec les lignes suivantes :
#if defined(WIN32) || defined(WIN64)
#if defined(_DEBUG)
_CrtSetDbgFlag ( _CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF );
_crtBreakAlloc = 120;
#endif
#endif
qui configurent l'outil d'analyse
(1) pour qu'à la fin d'exécution du programme sous debugger un rapport de l'utilisation dynamique de la mémoire soit établi et affiché
dans la fenêtre "Sortie" de Visual Studio,
(2) pour qu'un point d'arrêt pour le debugger soit placé lors de la 120ème opération d'allocation dynamique de mémoire (new, malloc,
calloc, ...).
Si on ne souhaite pas qu'un point d'arrêt soit réalisé, on pourra placer la ligne en commentaire.
La fenêtre de VisualStudio nommée "Pile des appels" permet de savoir où le point d'arrêt a été déclenché par le debugger.
a) Corriger le problème mémoire existant dans TestMemoire.cpp.
b) Ajouter l'ouverture d'une troisième fenêtre au programme DeuxFenetres.cpp permettant de visualiser la scène depuis un 3ème point de vue (au choix).
Solutions
![]()
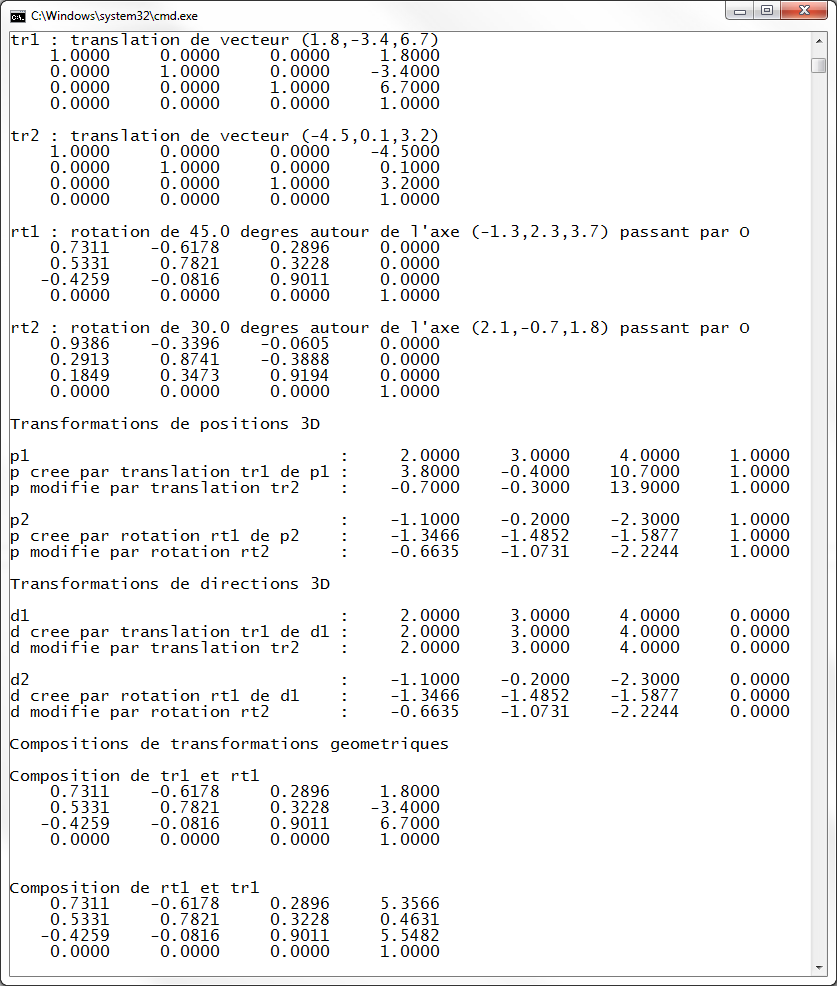
TD n°6 : Transformations géométriques en coordonnées homogènes
Exercice n°1
a) Développer en C++ une classe transformation géométrique 3D en coordonnées homogènes. Cette classe sera nommée TG3D.
b) Dériver de la classe TG3D une classe translation 3D pour le stockage d'opérateurs de type translation de vecteur (tx, ty, tz). Cette classe sera nommée Tr3D.
c) Dériver de la classe TG3D une classe rotation3D pour le stockage d'opérateurs de type rotation d'angle a autour de l'axe (ax, ay, az) passant par l'origine. Cette classe sera nommée Rt3D.
d) Implanter une méthode de transformation d'une position 3D ou d'une direction 3D par une translation 3D ou une rotation 3D (voir TD n°5 pour les classes Pos3D et Dir3D).
e) Implanter une méthode de composition d'une transformation géométrique 3D par une transformation géométrique 3D.
Solutions
|
CMD |
||
| Transformations géométriques 3D | ||
![]()
TP n°8 : Coordonnées homogènes et transformations géométriques
Exercice n°1
Télécharger le fichier zip suivant Mathematiques2.zip (il s'agit de la solution du TD n°6), extraire les fichiers qu'il contient, les compiler et vérifier la bonne exécution du résultat obtenu.
Exercice n°2
a) On ne dispose plus des opérateur OpenGL glTranslate, glRotate et glScale (c'est le cas par exemple en OpenGL ES ou en OpenGL standard lorsque
l'on développe des VertexShaders). A partir des classes de l'exercice n°1, développer une fonction permettant de composer dans cet ordre
une translation, une rotation et un zoom de façon à obtenir une transformation géométrique représentative de la suite de transformations que l'on
réalise sur le repère courant lorsque l'on doit placer, orienter et dimensionner un objet canonique (ou non) modélisé géométriquement.
La translation sera caractérisée par son déplacement (une direction). La rotation sera caractérisée par la direction de son axe et son angle en degrés.
Le zoom sera caractérisé par ses rapports réels selon les axes x, y et z.
Le prototype de la fonction pourrait donc être :
TG3D *transformationModelisation(Dir3D *tr,double angle,Dir3D *axe,double rx,double ry,double rz);
et elle aurait pour action de calculer et retourner une TG3D instanciée par new.
Précision : Les ajouts/modifications aux classes extraites de Mathematiques2.zip sont autorisés
même si ce n'est normalement pas nécessaire.
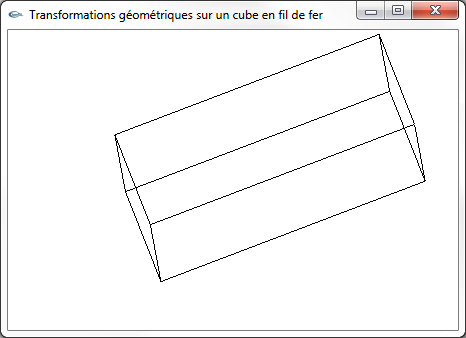
b) Utiliser la fonction de la question (a) pour développer un programme OpenGL dans lequel est modélisé un cube représenté en fil de fer placé, orienté
et dimensionné. On développera une fonction void modeliseCubeEnFilDeFer(TG3D *tg) qui modélisera le cube de coté 1.0 centré sur l'origine après
transformation par la TG3D tg.
Inclure dans le programme des contrôles clavier permettant de changer les paramètres d'appel de la fonction transformationModelisation.
On pourra s'aider des déclarations suivantes :
Pos3D pCube[8] = { Pos3D( 0.5F, 0.5F, 0.5F), Pos3D(-0.5F, 0.5F, 0.5F),
Pos3D( 0.5F,-0.5F, 0.5F), Pos3D(
0.5F, 0.5F,-0.5F),
Pos3D( 0.5F,-0.5F,-0.5F), Pos3D(-0.5F,
0.5F,-0.5F),
Pos3D(-0.5F,-0.5F, 0.5F), Pos3D(-0.5F,-0.5F,-0.5F)
};
int iCube [12][2] = { { 0,1 }, { 0,2 }, { 0,3 }, { 1,6 }, { 1,5 }, { 2,4 },
{ 2,6 }, { 3,4 },
{ 3,5 }, { 7,6 }, { 7,5 }, { 7,4 } } ;
Le tableau pCube contient les coordonnées des 8 sommets d'un cube de coté 1.0 centré sur l'origine. Le tableau iCube contient les couples
d'indices des douze arête d'un cube, ces indices référant à des positions dans le tableau pCube.
Cela signifie qu'il y a une arête entre les positions pCube[iCube[i][0]] et pCube[iCube[i][1]] pour tous les i entre 0 et 11.
c) Reprendre le développement réalisé aux (a) et (b) pour développer une classe TRZ3D dérivant de TG3D permettant d'assurer le même traitement.
Solutions
![]()
TP n°9 : Courbes lissées
On considère la liste de positions trois dimensions suivante :
( 6.5, 4.9,-3.00), ( 7.0, 5.0,-3.00), ( 7.5, 4.9,-2.00),
( 8.0, 4.6, 0.00), ( 7.5, 4.4, 2.00), ( 7.0, 4.2, 3.50),
( 6.0, 3.8, 4.00), ( 5.0, 2.8, 4.00), ( 4.0, 1.8, 4.00),
( 3.0, 0.8, 4.00), ( 0.0, 0.0, 4.00), (-1.4, 0.7, 3.75),
(-2.0, 2.0, 3.50), (-1.4, 3.3, 3.25), ( 0.0, 4.0, 3.00),
( 1.4, 3.3, 2.75), ( 2.0, 2.0, 2.50), ( 1.0, 0.7, 2.25),
(-1.0, 0.0, 2.00), (-2.4, 0.7, 1.75), (-3.0, 2.0, 1.50),
(-2.4, 3.3, 1.25), (-1.0, 4.0, 1.00), ( 0.4, 3.3, 0.75),
( 1.0, 2.0, 0.50), ( 0.0, 0.7, 0.25), (-2.0, 0.2, 0.00),
(-7.0, 0.0, 1.50), (-8.0, 0.0,-1.30), (-7.0, 0.3,-1.90),
(-6.0, 1.8,-2.40), (-4.5, 4.9,-2.40), (-3.0, 3.2,-2.40),
( 0.5, 2.4,-2.80), ( 3.5, 4.4,-2.80), ( 4.5, 4.7,-2.90),
( 5.5, 4.8,-3.00).
On souhaite dessiner une courbe lissant la ligne polygonale formée par ces 37 positions.
a) Réaliser un programme permettant d'afficher la ligne polygonale formée par ces 37 sommets.
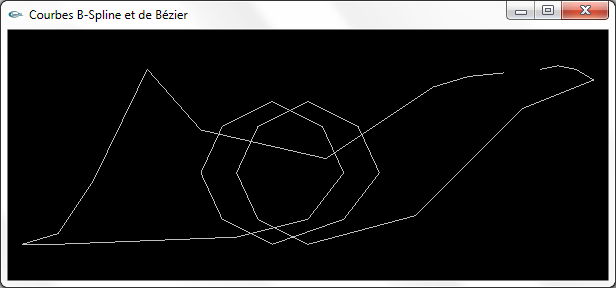
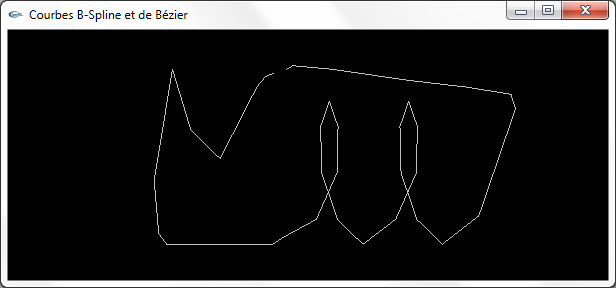
Deux vues de la ligne polygonale à 37 sommets
Si vous le souhaitez, vous pouvez vous aider du code source suivant BSplineEtBezierBase.cpp qui implante toute la partie OpenGL du code nécessaire, la déclaration des 37 points ci-dessus, mais où la fonction scene() se limite à afficher le segment de droite qui va du point d'indice 0 au point d'indice 36 c'est à dire le segment qui correspond au trou dans les images ci-dessus.
Notre but est maintenant de superposer cette ligne polygonale et une courbe lissée obtenue en l'utilisant comme liste de points de contrôle.
b) Développer une fonction permettant de modéliser une courbe de Bézier. Cette fonction pourrait avoir comme prototype
void bezier(int nbPoints,Pos3D **tPos,int n,GLenum typePrimitive);
et modélisera sous la forme d'une primitive OpenGL de type typePrimitive (GL_POINTS ou GL_LINE_STRIP) la courbe de Bézier calculée sur les nbPoints
Pos3D stockés dans le tableau tPos en créant n sommets de lissage (uniformément répartis entre t = 0.0 et t = 1.0).
Remarque : On peut éventuellement définir le paramètre tPos avec le type Pos3D * au lieu du type Pos3D**.
Utiliser cette fonction pour modifier le programme de la question (a) pour avoir les affichages simultanés de la ligne polygonale et de la courbe
de Bézier générée à partir d'elle.
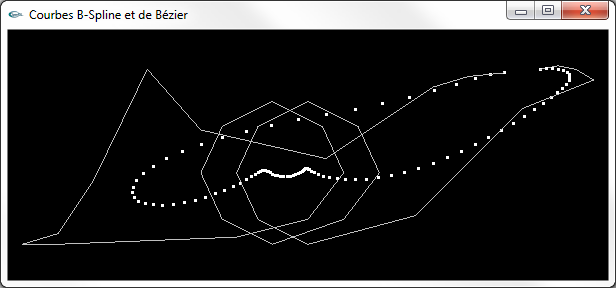

Courbe de Bézier avec 100 points (points de taille 3 pixels)
On notera le peu d'attractivité de la ligne polygonale sur la courbe de Bézier. On notera aussi que les points de la courbe de Bézier ne sont pas uniformément répartis sur la courbe même si on fait varier t uniformément. En effet, ils sont plus resserrés là où les points de contrôle sont plus resserrés.
c) Développer une fonction permettant de trouver la position d'un point de lissage, pour une valeur t donnée, sur une courbe B-Spline définie
par 4 points de contrôle et une matrice de base donnée.
Le prototype de cette fonction pourrait être
void positionSurBSpline(Pos3D **tPos,float t,float mb[4][4],Pos3D *point);
où tPos est le tableau des 4 points de contrôle, t est la valeur t, mb est la matrice de base et point est le point de lissage calculé.
Remarque : On peut éventuellement définir le paramètre tPos avec le type Pos3D * au lieu du type Pos3D**.
d) Utiliser la fonction développée à la question (c) pour développer une fonction permettant de modéliser une courbe B-Spline. Cette fonction pourrait
avoir comme prototype
void BSpline(int nbPoints,Pos3D **tPos,float mb[4][4], int n,GLenum typePrimitive);
et modélisera sous la forme d'une primitive OpenGL de type typePrimitive (GL_POINTS ou GL_LINE_STRIP) la courbe de B-Spline calculée sur les
nbPoints Pos3D stockés dans le tableau tPos en créant n sommets de lissage et en utilisant comme matrice de base la matrice mb.
Remarque : On peut éventuellement définir le paramètre tPos avec le type Pos3D * au lieu du type Pos3D**.
Attention, contrairement à l'implantation réalisée en cours, il convient ici de placer globalement n points et non (nbPoints-3)*n points. Il
ne doit pas non plus y avoir de duplication des points situés aux extrémités des morceaux de spline. Au lieu de modéliser explicitement les nbPoints-3
morceaux de spline, on fera varier uniformément t entre 0.0 et nbPoints-3.0, et pour chaque valeur t obtenue, on calculera le point de lissage pour
la valeur t-(int)t utilisée sur le vecteur géométrie numéro (int) t. C'est à dire qu'en calculant (int) t on détermine sur quel morceau de
spline vient se placer chaque valeur de t, et qu'avec t-(int)t on calcule la valeur effective de t sur ce morceau de spline (qui doit être, rappelons
le, comprise entre 0.0 et 1.0).
Utiliser cette fonction pour modifier le programme de la question (a) pour avoir les affichages simultanés de la ligne polygonale et de la courbe
de B-Spline NRU ou Catmull-Rom générée à partir d'elle.
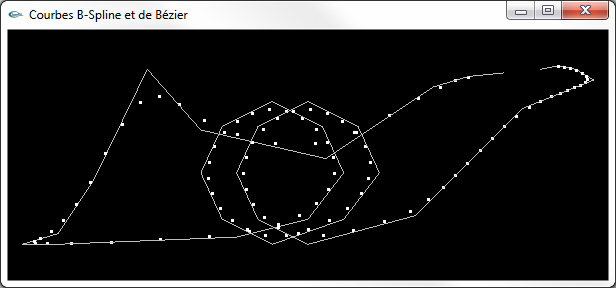

B-Spline NRU générée avec 100 points

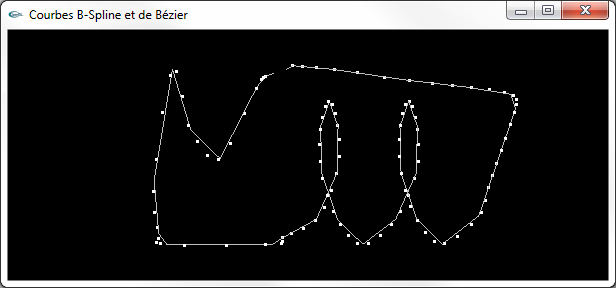
Spline de Catmull-Rom générée avec 100 points

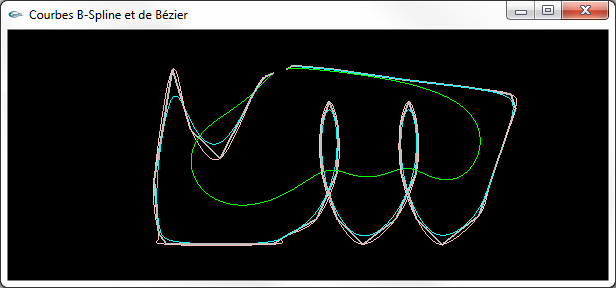
Courbes superposées
Solutions
|
CMD |
||
| Courbes B-Splines et de Bézier (implantation "C") | ||
| Courbes B-Splines et de Bézier (orienté objet) | ||
![]()
TP n°10 : Remplissage d'un triangle 2D
a) Télécharger le programme source RemplissageTriangle2DBase.cpp. Compiler et exécuter le.

Ce programme implante l'affichage d'un quadrillage 2D destiné à représenter un écran bitmap. La taille des pixels virtuels est de 16x16
pixels réels. La fonction permettant d'afficher le quadrillage est la fonction void quadrillage(void);.
Outre la fonction fond, ce programme comprend une fonction void pixel(int
x,int y); qui permet le dessin d'un pixel aux coordonnées (x,y) passées en paramètres. Cette fonction est utilisée 3 fois pour
dessiner 3 pixels de couleur respectives rouge, verte et jaune. Les coordonnées à fournir à cette fonction sont considérées dans le cadre du repère
virtuel associé au quadrillage et sont comptées en valeurs entières en cellules du quadrillage. La cellule de coordonnées (0,0) est située tout en
bas, tout à gauche. L'axe des x est orienté vers la droite. L'axe des y est orienté vers le haut. Si la fenêtre d'affichage est agrandie,
le quadrillage est agrandi d'autant sans subir de zoom ou de déformation.
Attention, l'élimination des parties cachées n'est pas activée. Tout nouveau dessin sera donc effectué en surimpression de ce qui a déjà
été dessiné.
Attention, les éclairages ne sont pas activés. Les couleurs de tracé sont donc à définir au moyen de la fonction glColor.
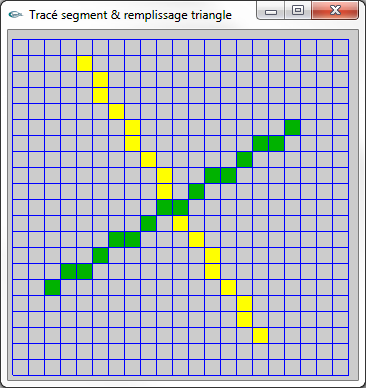
b) Modifier le programme de la question (a) pour y intégrer une fonction de dessin d'un segment de droite par algorithme de Bresenham et la tester
sur le tracé des segments de droite (15,2)-(4,19) et (2,5)-(17,15). Le prototype de cette fonction sera
void ligne(int xi,int yi,int xf,int yf);.
c) Modifier le programme de la question (a) pour y intégrer une fonction de rasterisation d'un triangle défini par 3 sommets et la tester sur
les triangles (15,2)-(2,4)-(19,14) et (1,6)-(18,16)-(4,19). Le protoype de cette fonction sera
void triangle(int x1,int y1,int x2,int y2,int x3,int y3);.
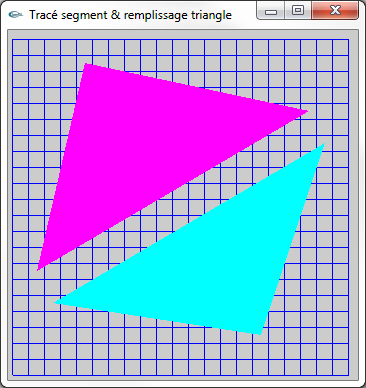

A gauche : les triangles réels
A droite : Les triangles rasterisés
Indications de développement
Le principe de la méthode de rasterisation consiste à tracer les unes après les autres les trames horizontales de pixels recouvrant le triangle. Le parcours est réalisé de la trame inférieure correspondant à la valeur minimale des y des 3 sommets du triangle jusqu'à la trame supérieure correspondant à la valeur maximale des y des 3 sommets du triangle. Par simplification, on va considérer que le sommet P1 dont les coordonnées (x1,y1) sont transmises en premiers paramètres est le sommet dont la coordonnée y possède la valeur minimale parmi y1, y2 et y3 et que le sommet P3 dont les coordonnées (x3,y3) sont transmises en derniers paramètres est le sommet dont la coordonnée y possède la valeur maximale parmi y1, y2 et y3. P2 de coordonnées (x2,y2) est donc le sommet intermédiaire en y. Dit autrement, on peut considérer que la propriété y1 <= y2 <= y3 est vérifiée de manière certaine.
Méthode 1 pour la détermination des trames horizontales
Tracer une trame horizontale de pixels nécessite de connaître l'abscisse xg du pixel le plus à gauche et l'abscisse xd du pixel le plus à
droite sur cette trame. Une simple itération de xg à xd inclus permettra le tracé de la trame. Le problème de détermination des valeurs xg et xd
sur chaque trame d'ordonnée y peut être vu comme un problème de parcours des bords gauche et droit du triangle. La détermination de ces bords
est donc nécessaire. On sait que le coté P1‑P3 est le coté qui va du sommet le plus bas au sommet le plus haut et que donc il constituera à
lui seul soit le bord droit soit le bord gauche. Le sommet P2 est situé soit à droite soit à gauche de la droite P1‑P3. S'il est à gauche,
le bord gauche est constitué des deux cotés P1‑P2 et P2‑P3 et le bord droit du seul coté P1‑P3. S'il est à droite, le bord
droit est constitué des deux cotés P1‑P2 et P2‑P3 et le bord gauche du seul coté P1‑P3. Le problème est donc de déterminer de quel
coté de la droite P1‑P3 est placé le sommet P2. Indice : produit vectoriel.
Les cotés des bords étant déterminés, le dernier problème à résoudre consiste à déterminer les pixels qui les composent, c'est à dire plus précisément
à déterminer un x pour chaque y sur les bords gauche et droits. Ce problème se rapporte à un problème de rasterisation de segments de droite. On
utilisera ici un algorithme directement issu de l'algorithme de Bresenham. Conseil : Quoi que peu optimal du point de vue des temps de calcul
(encore que), le développement gagne beaucoup en simplicité et en lisibilité si on utilise des tableaux d'entiers xg[y] et xd[y] remplis par
une fonction de rasterisation des cotés qui sera appelée 3 fois, c'est à dire une fois sur P1‑P2 pour remplir xg ou xd, une fois sur P2‑P3
et une fois sur P1‑P3 pour remplir xg ou xd. Une fois ces tableaux remplis, le dessin effectif peut être réalisé.
Méthode 2 pour la détermination des trames horizontales
Tracer une trame horizontale de pixels nécessite de connaître les abscisses xmin et xmax des pixels initiaux et finaux de cette trame. Une fois ces valeurs connues, une simple itération de xmin à xmax inclus permettra le tracé de la trame. Le problème de détermination des valeurs xmin et xmax sur chaque trame d'ordonnée y peut être vu comme un problème de rasterisation des cotés du triangle. Cette rasterisation n'a pas pour but direct le tracé, mais la détermination de xmin et xmax pour chaque y à partir des pixels déterminés par rastérisation sur le principe qu'aucun pixel du triangle ne saurait être extérieur au triangle et donc extérieur par rapport à ses cotés. On utilisera ici un algorithme directement issu de l'algorithme de Bresenham. Conseil : Quoi que peu optimal du point de vue des temps de calcul (encore que), le développement gagne beaucoup en simplicité et en lisibilité si on utilise des tableaux d'entiers xmin[y] et xmax[y] remplis par une fonction de rasterisation des cotés qui sera appelée 3 fois, c'est à dire une fois sur P1‑P2 sur xmin et sur xmax, une fois sur P2‑P3 sur xmin et sur xmax et une fois sur P1‑P3 sur xmin et sur xmax. Une fois ces tableaux remplis, le dessin effectif peut être réalisé.
Solutions
|
CMDD |
||
| Tracé de segments de droite par algorithme de Bresenham, remplissage d'un triangle 2D version 1 | ||
| Tracé de segments de droite par algorithme de Bresenham, remplissage d'un triangle 2D version 2 | ||
![]()
TP n°11 : Lancer de rayons : Calcul des directions de réflexion et transmission
Parmi l'ensemble des problèmes devant être résolus pour l'implantation de l'algorithme de lancer de rayons, on trouve le calcul des rayons
réfléchis spéculairement et transmis lors d'un changement de milieu subi par un rayon. Ce TP porte sur l'implantation de ces calculs. Les
formules mathématiques peuvent être trouvées dans le cours sur le lancer de rayons.
Le fichier Mathematiques.zip reprend les classes de modélisation de coordonnées homogènes et de
transformations géométriques en 3D développées au cours des TD n°5 et n°6. Le travail demandé dans ce TP consiste dans un premier temps à ajouter
à ces classes les méthodes de calcul des directions de réflexion et de transmission, puis à valider leur fonctionnement, et enfin à utiliser ces
classes ainsi modifiées pour la compilation de deux programmes :
- un programme de caractérisation de ces phénomènes par visualisation en mode graphique de ces direction,
- un programme de lancer de rayons.
a) Concevoir une méthode de la classe Dir3D permettant de calculer la direction d'un rayon réfléchi spéculairement.
Son prototype sera :
int reflexion(Dir3D *i,Dir3D *n);
La méthode développée doit fonctionner de la manière suivante :
- S'il y a une réflexion, elle retourne 1 et affecte this avec la direction de réflexion calculée à partie de la direction incidente normée
i et de la normale (normée) n.
- S'il n'y a pas de réflexion, 0 est retourné et this est inchangé.
La situation où il n'y a pas de réflexion est rencontrée lorsque le rayon incident présente un angle supérieur à 90° avec la normale à l'interface
au point d'incidence. Cette situation est détectable dans la formule de calcul par un test sur le produit scalaire de n par i qui doit être supérieur
ou égal à 0.0 pour qu'une réflexion ait lieu.
Les figures 1, 2 et 3 ci-dessous donnent quelques jeux de valeurs (direction de normale, direction d'incidence, direction de réflexion spéculaire
à obtenir) dont vous pouvez vous servir pour valider votre fonction.
b) Concevoir une méthode de la classe Dir3D permettant de calculer la direction d'un rayon transmis à l'interface entre deux milieux lors
du passage entre ces deux milieux.
Son prototype sera :
int transmission(Dir3D *i,Dir3D *n,double niSurNt);
La méthode développée doit fonctionner de la manière suivante :
- S'il y a une transmission, elle retourne 1 et affecte this avec la direction de transmission calculée à partir de la direction incidente
normée i, de la normale (normée) n et du rapport niSurNt entre les indices de réfraction des milieux incident et de transmission.
- S'il n'y a pas de transmission, 0 est retourné et this est inchangé.
La situation où il n'y a pas de transmission est rencontrée lorsque ni/nt*sin(Θi) est supérieur à 1.0 (voir cours sur le lancer de
rayon). Cette situation est détectable dans la formule par un test portant sur la valeur dont on calcule la racine carrée, valeur qui doit être supérieure
ou égale à 0.0 pour que la racine existe et soit réelle et qu'il y ait donc transmission.
Les figures 1, 2 et 3 ci-dessous donnent quelques jeux de valeurs (direction de normale, direction d'incidence, indices de réfraction ni et nt,
direction de transmission à obtenir) dont vous pouvez vous servir pour valider votre fonction.
Précision : Les valeurs des figures ci-dessous sont des valeurs arrondies à 4 chiffres après la virgule. Il faut donc s'attendre à ce que vos
résultats présentent des différences par rapport à ceux affichés ci-dessous. Elles devraient être mineures.


Fig 1 : Rayon incident en jaune, normale en magenta, rayon réfléchi en rouge, rayon transmis en bleu
ni > nt -> Rayon transmis dévié vers le plan d'interface


Fig 2 : ni < nt -> Rayon transmis dévié vers le vecteur opposé au vecteur normal
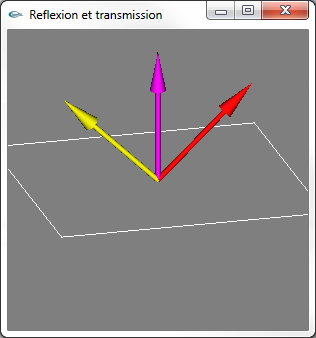

Fig 3 : Cas particulier, pas de rayon transmis
c) Télécharger le fichier ReflexionEtTransmission.zip. Extraire les fichiers qu'il contient. Créer un projet de développement intégrant les fichiers .cpp du fichier zip et les fichiers .cpp des questions (a) et (b). Effectuer la compilation du projet. L'exécution devrait conduire aux affichages réalisés aux figures 1, 2 et 3.
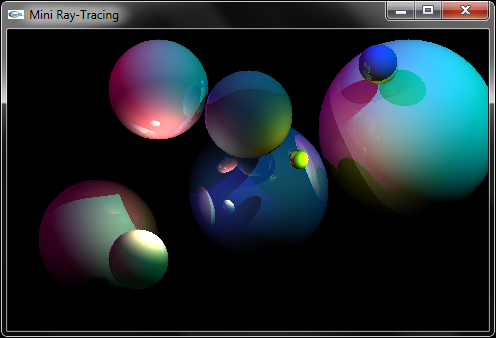
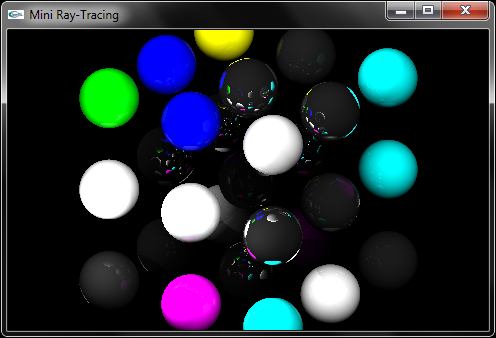
d) Télécharger le fichier RayTracing.zip (fonction main dans RayTracing.cpp). Extraire les fichiers
qu'il contient. Créer un projet de développement intégrant les fichiers .cpp du fichier zip et les fichiers .cpp des questions (a) et (b). Effectuer
la compilation de votre projet. L'exécution devrait conduire aux affichages réalisés ci-dessous. Ce programme implante un calcul d'images
par lancer de rayons. Les scènes sont constituées de sphères. Le programme ouvre deux fenêtres. Dans la première, un Z-Buffer est utilisé pour l'affichage.
Dans la seconde, la même scène est affichée en lancer de rayons. Les contrôles implantés sont les suivants :
- Espace pour switcher entre les scènes
- Enter pour lancer le calcul de lancer de rayons
- Touches de curseur et souris pour manipuler la scène dans le fenêtre OpenGL
- +/- pour augmenter/diminuer le niveai de récursivité maximum du lancer de rayon

Solutions
|
GLUt |
||
| Calcul des directions de réflexion et transmission (validation texte) | ||
| Calcul des directions de réflexion et transmission (validation graphique) | ||
| Calcul des directions de réflexion et transmission (Application au lancer de rayons) | ||
![]()
TP n°12 : Calcul de la quantité d'énergie diffusée en un point éclairé par une source lumineuse
Les calculs de diffusion sont fondamentaux en informatique graphique. En effet, une large part du fait que les objets de nos scènes soient visibles
est le résultat de phénomènes de réflexion diffuse. C'est en particulier ce phénomène qui est majoritairement responsable de la "couleur"
apparente des objets.
Ce TP propose de réaliser l'implantation du calcul de diffusion par la méthode de Lambert. Il s'agit essentiellement de calculs mathématiques
simples dont le but est, connaissant les caractéristiques d'une source lumineuse et les caractéristiques matérielles de l'objet éclairé par
la source lumineuse, de calculer l'énergie diffusée sur cet objet. Une application pratique est proposée sous la forme d'un programme complet
implantant d'une part l'affichage d'une sphère en utilisant les calculs de diffusions d'OpenGL et d'autre part l'affichage
de cette sphère en utilisant nos propres formules de calcul.
Remarque : L'implantation des calculs de diffusion est quelque chose de très classique en informatique graphique. Vous devrez le faire si vous
développez un programme de rendu par lancer de rayons. Ce sera aussi le cas si vous développez en utilisant certaines versions récentes d'OpenGL
où pour alléger la bibliothèque ou rendre possible des implantations différentes (plus simples, plus élaborées), les calculs d'illumination ont
été retirés et avec pour conséquence que leur programmation est à la charge du développeur.
On considère les classes Rvb, Couleur, Energie suivantes :
- Rvb.h
- Rvb.cpp
- Couleur.h
- Couleur.cpp
- Energie.h
- Energie.cpp
La classe mère Rvb permet le stockage d'une information rvb à composantes réelles.
La classe Couleur dérive de Rvb et est utilisée pour coder des couleurs rvb ou des coefficients rvb colorés (composantes comprises entre 0.0 et 1.0).
La classe Energie dérive de Rvb et est utilisée pour coder une énergie colorée (composantes comprises entre 0.0 et +µ).
On pourra utiliser les classes mathématiques développées dans les TD et les TP précedents pour gérer les positions en 3D et les directions en 3D.
Ces classes sont disponibles dans l'archive Mathematiques.zip.
a) On considère les classes Lumiere et LumiereDirectionnelle suivantes :
- Lumiere.h
- Lumiere.cpp
- LumiereDirectionnelle.h
- LumiereDirectionnelle.cpp
La classe mère Lumiere permet le stockage d'une lumière par la définition de ses attributs de couleur, d'intensité d'émission et d'activation/désactivation.
Elle n'est pas destinée à être instanciée.
La classe LumiereDirectionnelle dérive de Lumiere et implante une lumière directionnelle par la définition d'un attribut supplémentaire donnant
la direction d'émission de la lumière.
Développer une méthode permettant de calculer la quantité d'énergie diffusée sous l'éclairage d'une LumiereDirectionnelle en une Position3D
sur un objet où la normale est connue sous la forme d'une Direction3D. Les coefficients de diffusion de la surface sont définis par la donnée
d'une Couleur. La formule de calcul à utiliser est la formule de Lambert : L
= Ip Kd (![]() .
.![]() ).
).

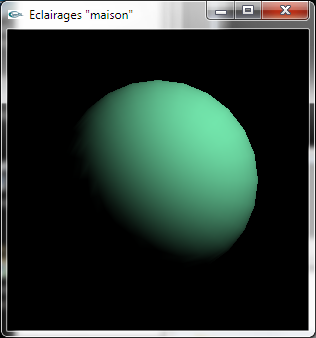

Sphère éclairée par une lumière directionnelle
en pur OpenGL à gauche, en utilisant le calcul de diffusion "maison" à droite
Pour cette question, il convient de développer une méthode purement virtuelle dans la classe Lumiere qui sera implantée concrètement dans la classe
LumiereDirectionnelle. Son prototype est:
virtual void energieDiffusee(Energie *e,Pos3D *p,Dir3D *n,Couleur *kd)
où e est l'énergie diffusée (à calculer), p la position du point de diffusion, n la normale à l'objet au point p et kd le coefficient de
diffusion de l'objet au point p.
Remarque : Pour le calcul de diffusion de Lambert sous une lumière directionnelle, la position p n'est pas utilisée. Elle apparaît dans le prototype
pour compatibilité de la méthode virtuelle avec d'autres types de lumières où la connaissance de cette position est nécessaire.
b) On considère la classe LumierePonctuelle suivante :
- LumierePonctuelle.h
- LumierePonctuelle.cpp
La classe LumierePonctuelle dérive de Lumiere et implante une lumière ponctuelle par la définition de deux attributs supplémentaires définissant
la position de la lumière et un booléen indiquant s'il y a ou non atténuation de l'illumination en fonction de la distance entre la source
lumineuse et le point qu'elle éclaire.
Développer une méthode permettant de calculer la quantité d'énergie diffusée sous l'éclairage d'une LumierePonctuelle en une Position3D extraite d'une surface où la normale est connue sous la forme d'une Direction3D. Les coefficients de diffusion de la surface sont définis par la donnée d'une Couleur.
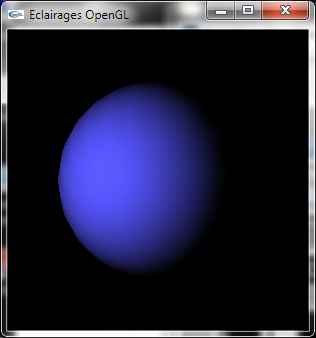
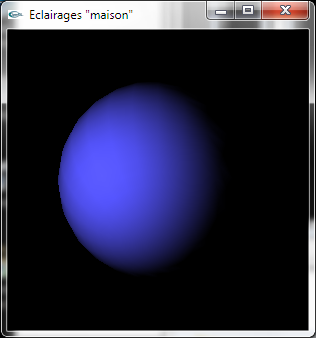

Sphère éclairée par une lumière ponctuelle
en pur OpenGL à gauche, en utilisant le calcul de diffusion "maison" à droite
Pour cette question, il convient de développer une nouvelle implantation de la méthode de calcul de diffusion dans la classe LumierePonctuelle.
c) On pourra utiliser le programme DiffusionsLambertiennes.cpp pour tester les deux méthodes
développées. Ce programme n'a pas à être modifié. Il utilise les méthodes de calcul de diffusion selon les prototypes définis ci-dessus.
Ce programme affiche deux fenêtres avec, dans la première, une sphère éclairée au moyen de l'implantation OpenGL du calcul de diffusion de Lambert
et dans la seconde, une sphère éclairée au moyen de l'implantation réalisée par nos soins. Vous remarquerez que la fonction de modélisation de
sphère utilisée pour afficher selon nos calculs de diffusion marche en GL_LIGHTING désactivé et définit donc les couleurs des vertices de la sphère
en utilisant des couleurs "classiques" spécifiées par glColor3f. Ces couleurs sont calculées en utilisant nos méthodes de calcul.
Remarque: Ce code source montre comment GLUt permet d'utiliser deux (plusieurs par extension) fenêtres ainsi que les menus popup.
Solutions
![]()
Hiérarchie de classes
| Vecteur4 | CoordonneesHomogenes3D | Position3D | ||||
| Dimension3D | ||||||
| Matrice4x4 | TransformationGeometrique3D | Translation3D | ||||
| MatriceDeBase | Rotation3D | |||||
| Scale3D | ||||||
| LookAt | ||||||
| Rvb | Couleur | |||||
| Energie | ||||||
| Lumiere | LumierePonctuelle | LumiereSpot | ||||
| LumiereDirectionnelle | ||||||
| Materiel | ||||||
| Objet | Sphere | |||||
![]()