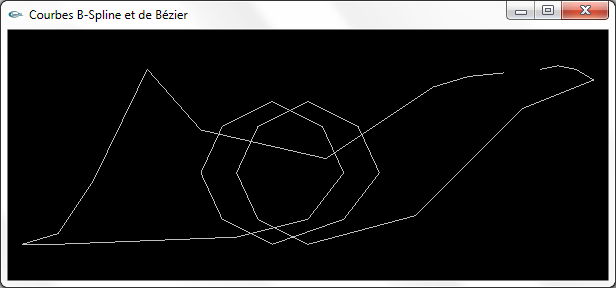
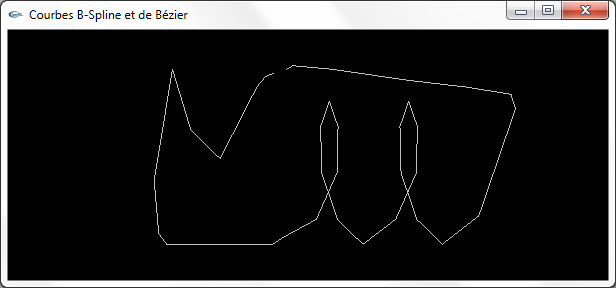
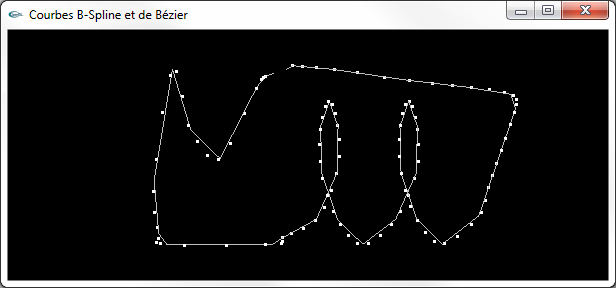
Deux vues de la ligne polygonale à 37 sommets
Commentaires
Le développement a été réalisé en utilisant des tableaux de pointeurs sur Pos3D.
Trois classes ont été développées :
- LignePolygonale3D permet de représenter une ligne polygonale composée de nbPoints sommets stockés dans un tableau tPos de Pos3D. nbPoints
et tPos sont définis en attribut dans cette classe.
- Matrice4x4 permet de stocker des matrice de 4x4 float. Il s'agit d'une classe mère comportant un attribut c de type tableau 4x4
de float.
- MatriceDeBase permet de stocker des matrices de base. Cette classe dérive de Matrice4x4. Cette classe n'a pas d'attribut d'instance
en propre, mais comporte deux attributs de classe nommés NRUBS et CATMULL_ROM initialisés avec les valeurs des matrices de base B-Spline non rationnelle
uniforme et Catmull-Rom.
Les questions du TP ont été développées sous la forme de constructeurs pour la classe LignePolygonale3D.
Dans le constructeur de génération d'une courbe de Bézier les Cni sont précalculés dans le tableau de long long nommé cn
de façon à ce que n puisse aller jusqu'à la valeur 62 (détermination expérimentale réalisée par ailleurs). Si on souhaite dépasser cette valeur,
il faut alors envisager d'utiliser un type de base réel pour le tableau cn. Ce précalcul a pour but d'optimiser les performances globales
de calcul de la courbe de Bézier.


Deux vues de la ligne polygonale à 37 sommets
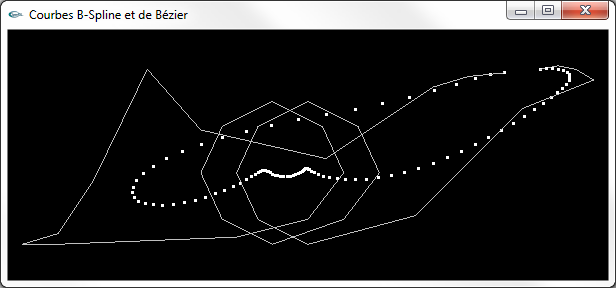

Courbe de Bézier avec 100 points (points de taille 3 pixels)
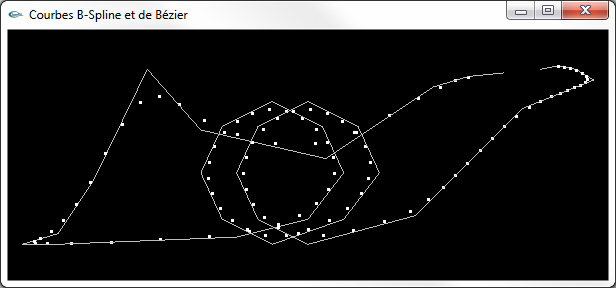

B-Spline NRU générée avec 100 points

Spline de Catmull-Rom générée avec 100 points

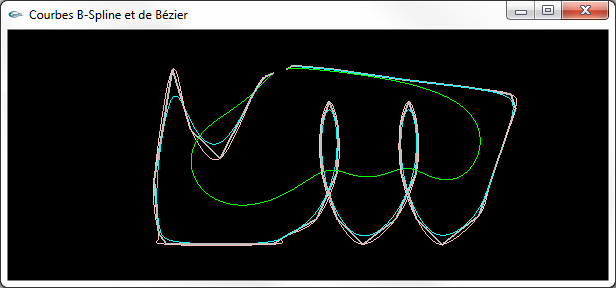
Courbes superposées (plusieurs centaines de points sur chaque courbe lissée)
Bézier en vert, B-Spline NRU en cyan, Spline de Catmull-Rom en rose
Tous les fichiers sources : BSplineEtBezierOO.zip
Fichier source : BSplineEtBezierOO.cpp
static int nbp = 100;
static LignePolygonale3D *lp = NULL;
/* Scene dessinee */
static void scene(void) {
switch (aff) {
case 0 :
glColor3f(0.75F,0.75F,0.75F);
lp->drawOpenGL(GL_LINE_STRIP);
break;
case 1 :
glColor3f(0.75F,0.75F,0.75F);
glPointSize(3.0);
lp->drawOpenGL(GL_LINE_STRIP);
glColor3f(1.0F,1.0F,1.0F);
{ LignePolygonale3D *lpl = new LignePolygonale3D(nbp,lp,&MatriceDeBase::NRUBS);
lpl->drawOpenGL(GL_POINTS);
delete(lpl); }
break;
case 2 :
glColor3f(0.75F,0.75F,0.75F);
lp->drawOpenGL(GL_LINE_STRIP);
glPointSize(3.0);
glColor3f(1.0F,1.0F,1.0F);
{ LignePolygonale3D *lpl = new LignePolygonale3D(nbp,lp,&MatriceDeBase::CATMULL_ROM);
lpl->drawOpenGL(GL_POINTS);
delete(lpl); }
break;
case 3 :
glColor3f(0.75F,0.75F,0.75F);
glPointSize(3.0);
lp->drawOpenGL(GL_LINE_STRIP);
glColor3f(1.0F,1.0F,1.0F);
{ LignePolygonale3D *lpl = new LignePolygonale3D(nbp,lp);
lpl->drawOpenGL(GL_POINTS);
delete(lpl); }
break;
case 4 :
glLineWidth(2.0F);
glColor3f(0.75F,0.75F,0.75F);
lp->drawOpenGL(GL_LINE_STRIP);
glLineWidth(1.0F);
glColor3f(0.0F,1.0F,1.0F);
{ LignePolygonale3D *lpl = new LignePolygonale3D(nbp,lp,&MatriceDeBase::NRUBS);
lpl->drawOpenGL(GL_POINTS);
delete(lpl); }
glColor3f(1.0F,0.75F,0.75F);
{ LignePolygonale3D *lpl = new LignePolygonale3D(nbp,lp,&MatriceDeBase::CATMULL_ROM);
lpl->drawOpenGL(GL_POINTS);
delete(lpl); }
glColor3f(0.0F,1.0F,0.0F);
{ LignePolygonale3D *lpl = new LignePolygonale3D(nbp,lp);
lpl->drawOpenGL(GL_POINTS);
delete(lpl); }
break; }
}
Fichier source : LignePolygonale3D.h
/* Ligne polygonale 3D */
/* */
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Mars 2020 */
#ifndef ____LIGNEPOLYGONALE3D____
#define ____LIGNEPOLYGONALE3D____
#include <GL/gl.h>
#include "Pos3D.h"
class MatriceDeBase;
class LignePolygonale3D {
public :
/* Nombre de sommets */
int nbPoints;
/* Tableau des sommets */
Pos3D **tPos;
/* Stack pointer */
int sp;
public :
/* Constructeur "vide" */
/* (nbPoints=0, tPos = NULL) */
LignePolygonale3D(void);
/* Constructeur pour une ligne polygonale */
/* de n sommets */
LignePolygonale3D(int n);
/* Constructeur pour une ligne polygonale */
/* de n sommets initialisee avec le contenu */
/* du tableau tPos */
LignePolygonale3D(int n,Pos3D **tPos);
/* Constructeur de clonage */
LignePolygonale3D(LignePolygonale3D *lp);
/* Constructeur pour une ligne polygonale */
/* de n sommets lissee par B-Spline */
/* a partir de la ligne polygonale lp */
/* en utilisant la matrice de base m */
LignePolygonale3D(int n,LignePolygonale3D *lp,const MatriceDeBase *m);
/* Constructeur pour une ligne polygonale */
/* de n sommets lissee par Bezier */
/* a partir de la ligne polygonale lp */
LignePolygonale3D(int n,LignePolygonale3D *lp);
/* Destructeur */
~LignePolygonale3D(void);
void add(Pos3D *p);
void setPosition(int pos,Pos3D *p);
void print(void);
void drawOpenGL(GLenum typePrimitive);
};
#endif
Fichier source : LignePolygonale3D.cpp
/* Ligne polygonale 3D */
/* */
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Mars 2020 */
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <GL/glut.h>
#include <GL/gl.h>
#include <GL/glu.h>
#include "Pos3D.h"
#include "LignePolygonale3D.h"
#include "MatriceDeBase.h"
/* Constructeurs */
LignePolygonale3D::LignePolygonale3D(void) {
nbPoints = 0;
tPos = NULL;
sp = 0;
}
LignePolygonale3D::LignePolygonale3D(int nbPoints) {
this->nbPoints = nbPoints;
tPos =(Pos3D **) calloc(nbPoints,sizeof(Pos3D *));
for ( int i = 0 ; i < nbPoints ; i++ )
tPos[i] = new Pos3D();
sp = 0;
}
LignePolygonale3D::LignePolygonale3D(int nbPoints,Pos3D **tPos) {
this->nbPoints = nbPoints;
this->tPos =(Pos3D **) calloc(nbPoints,sizeof(Pos3D *));
for ( int i = 0 ; i < nbPoints ; i++ ) {
this->tPos[i] = new Pos3D(tPos[i]); }
sp = nbPoints;
}
LignePolygonale3D::LignePolygonale3D(LignePolygonale3D *lp) {
nbPoints = lp->nbPoints;
tPos =(Pos3D **) calloc(nbPoints,sizeof(Pos3D *));
for ( int i = 0 ; i < nbPoints ; i++ ) {
tPos[i] = new Pos3D(lp->tPos[i]); }
sp = lp->sp;
}
/* Destructeur */
LignePolygonale3D::~LignePolygonale3D(void) {
if ( nbPoints != 0 ) {
if ( tPos ) {
for ( int i = 0 ; i < nbPoints ; i++)
delete(tPos[i]);
free(tPos);
tPos = NULL; } }
}
/* Calcul la position d'un point sur une courbe */
/* B-Spline controlee par quatre points */
/* tPos : le tableau des 4 points de controle */
/* t : la valeur de calcul du point */
/* t a prendre dans l'intervalle [0.0,1.0] */
/* mb : la matrice de base */
/* point : le point resultat */
static void positionSurBSpline(Pos3D **tPos,float t,const MatriceDeBase *mb,Pos3D *point) {
float vt[4] = { t*t*t,t*t,t,1.0F };
float vtmb[4] = { 0.0F,0.0F,0.0F,0.0F };
for ( int j = 0 ; j < 4 ; j++ ) {
for ( int k = 0 ; k < 4 ; k++ )
vtmb[j] += vt[k] * mb->c[k][j] ; }
point->x = point->y = point->z = 0.0;
for ( int j = 0 ; j < 4 ; j++ ) {
point->x += vtmb[j] * tPos[j]->x ;
point->y += vtmb[j] * tPos[j]->y ;
point->z += vtmb[j] * tPos[j]->z ; }
}
LignePolygonale3D::LignePolygonale3D(int nbPoints,LignePolygonale3D *lp,const MatriceDeBase *m) {
this->nbPoints = nbPoints;
tPos =(Pos3D **) calloc(nbPoints,sizeof(Pos3D *));
for ( int i = 0 ; i < nbPoints ; i++ ) {
tPos[i] = new Pos3D();
float t = i/(nbPoints-1.0)*(lp->nbPoints-3);
int nb =(int) t;
if ( nb == lp->nbPoints-3 )
nb = lp->nbPoints-4;
positionSurBSpline(&(lp->tPos[nb]),t-nb,m,tPos[i]); }
}
LignePolygonale3D::LignePolygonale3D(int nbPoints,LignePolygonale3D *lp) {
this->nbPoints = nbPoints;
tPos =(Pos3D **) calloc(nbPoints,sizeof(Pos3D *));
long long *cn;
cn =(long long *) calloc(lp->nbPoints,sizeof(long long));
cn[0] = 1;
cn[1] = lp->nbPoints-1;
for ( int i = 2 ; i < lp->nbPoints ; i++ )
cn[i] = (cn[i-1]*(lp->nbPoints-i))/i;
for ( int i = 0 ; i < nbPoints ; i++ ) {
tPos[i] = new Pos3D();
float t =(float) i/(nbPoints-1);
float mt = 1.0F-t;
for ( int j = 0 ; j < lp->nbPoints ; j++ ) {
float fac = cn[j]*pow(t,j)*pow(mt,lp->nbPoints-1-j);
tPos[i]->x += fac * lp->tPos[j]->x;
tPos[i]->y += fac * lp->tPos[j]->y;
tPos[i]->z += fac * lp->tPos[j]->z; } }
free(cn);
}
void LignePolygonale3D::add(Pos3D *p) {
tPos[sp]->x = p->x;
tPos[sp]->y = p->y;
tPos[sp]->z = p->z;
sp++;
}
void LignePolygonale3D::setPosition(int pos,Pos3D *p) {
tPos[pos]->x = p->x;
tPos[pos]->y = p->y;
tPos[pos]->z = p->z;
}
void LignePolygonale3D::print(void) {
for ( int i = 0 ; i < nbPoints ; i++ ) {
tPos[i]->print();
printf("\n"); }
}
void LignePolygonale3D::drawOpenGL(GLenum typePrimitive) {
glBegin(typePrimitive);
for ( int i = 0 ; i < nbPoints ; i++ ) {
glVertex3f(tPos[i]->x,tPos[i]->y,tPos[i]->z); }
glEnd();
}
/* Mathematiques de l'informatique graphique */
/* Matrice de 4x4 double */
/* */
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Mars 2014 */
#ifndef ____MATRICE4X4____
#define ____MATRICE4X4____
class Vecteur4;
class Matrice4x4 {
public :
float c[4][4];
public :
/* Constructeurs */
Matrice4x4(void);
Matrice4x4(float *t);
Matrice4x4(float **t);
Matrice4x4(Matrice4x4 *tg);
/* Destructeur */
~Matrice4x4(void);
/* Methodes */
void print(void);
};
#endif
Fichier source : Matrice4x4.cpp
/* Mathematiques de l'informatique graphique */
/* Matrice de 4x4 float */
/* */
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Mars 2014 */
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include "Matrice4x4.h"
/* Constructeurs */
Matrice4x4::Matrice4x4(void) {
for ( int i = 0 ; i < 4 ; i++ )
for ( int j = 0 ; j < 4 ; j++ )
c[i][j] = 0.0;
}
Matrice4x4::Matrice4x4(float *t) {
int k = 0;
for ( int i = 0 ; i < 4 ; i++ )
for ( int j = 0 ; j < 4 ; j++ ) {
c[i][j] = t[k];
k++; }
}
Matrice4x4::Matrice4x4(float **t) {
for ( int i = 0 ; i < 4 ; i++ )
for ( int j = 0 ; j < 4 ; j++ )
c[i][j] = t[i][j];
}
Matrice4x4::Matrice4x4(Matrice4x4 *tg) {
for ( int i = 0 ; i < 4 ; i++ )
for ( int j = 0 ; j < 4 ; j++ )
c[i][j] = tg->c[i][j];
}
/* Destructeur */
Matrice4x4::~Matrice4x4(void) {
}
/* Methodes */
void Matrice4x4::print(void) {
for ( int i = 0 ; i < 4 ; i++ )
printf("%10.4f %10.4f %10.4f %10.4f\n",c[i][0],c[i][1],c[i][2],c[i][3]);
}
Fichier source : MatriceDeBase.h
/* Mathematiques de l'informatique graphique */
/* Matrice de base pour des courbes B-Splines */
/* */
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Mars 2014 */
#ifndef ____MATRICEDEBASE____
#define ____MATRICEDEBASE____
#include "Matrice4x4.h"
class MatriceDeBase : public Matrice4x4 {
public :
static const MatriceDeBase NRUBS;
static const MatriceDeBase CATMULL_ROM;
public :
/* Constructeurs */
MatriceDeBase(void);
MatriceDeBase(float *t);
MatriceDeBase(float **t);
MatriceDeBase(MatriceDeBase *tg);
/* Destructeur */
~MatriceDeBase(void);
};
#endif
Fichier source : MatriceDeBase.cpp
/* Mathematiques de l'informatique graphique */
/* Matrice de base pour des courbes B-Splines */
/* */
/* Auteur: Nicolas JANEY */
/* nicolas.janey@univ-fcomte.fr */
/* Mars 2020 */
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include "MatriceDeBase.h"
/* Constructeurs */
MatriceDeBase::MatriceDeBase(void) {
for ( int i = 0 ; i < 4 ; i++ )
for ( int j = 0 ; j < 4 ; j++ )
c[i][j] =( i == j ) ? 1.0F : 0.0F;
}
MatriceDeBase::MatriceDeBase(float *t):Matrice4x4(t) {
}
MatriceDeBase::MatriceDeBase(float **t):Matrice4x4(t) {
}
MatriceDeBase::MatriceDeBase(MatriceDeBase *m):Matrice4x4(m) {
}
/* Destructeur */
MatriceDeBase::~MatriceDeBase(void) {
}
static float vl1[] = { -1.0F/6.0F, 3.0F/6.0F, -3.0F/6.0F, 1.0F/6.0F,
3.0F/6.0F,-6.0F/6.0F, 3.0F/6.0F, 0.0F,
-3.0F/6.0F, 0.0F, 3.0F/6.0F, 0.0F,
1.0F/6.0F, 4.0F/6.0F, 1.0F/6.0F, 0.0F };
const MatriceDeBase MatriceDeBase::NRUBS(vl1);
static float vl2[] = { -1.0F/2.0F, 3.0F/2.0F, -3.0F/2.0F, 1.0F/2.0F,
2.0F/2.0F,-5.0F/2.0F, 4.0F/2.0F,-1.0F/2.0F,
-1.0F/2.0F, 0.0F, 1.0F/2.0F, 0.0F,
0.0F, 2.0F/2.0F, 0.0F, 0.0F };
const MatriceDeBase MatriceDeBase::CATMULL_ROM(vl2);