Les calculs d'ombrage:
la lumière, les matériaux
D'OMBRAGE
LUMIÈRES ET
MATÉRIAUX
AU SEIN
DES LIBRAIRIES 3D
On dispose d'un objet pour lequel on désire calculer la couleur sous un éclairage. Cet objet peut être constitué de surfaces planes, courbes ou d'un ensemble de facettes.
En première approximation, la couleur de chaque pixel dépend de la quantité de lumière frappant l'objet en ce pixel (quantité de lumière par unité de surface) et d'une couleur intrinsèque.
Une boite éclairée
Approximation très (trop) forte de la réalité.
-> Modélisation des phénomènes physiques se déroulant lorsque de la lumière touche une surface.
Propagation des rayons lumineux
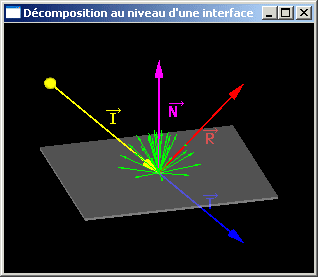
A l'interface entre deux milieux, un rayon lumineux incident est scindé en plusieurs composantes distinctes:
- absorbée,
- diffusée
- réfléchie spéculairement,
- transmise.
L'énergie totale reçue à l'interface est redistribuée entre ces différentes composantes.
| Décomposition de la lumière au niveau d'une interface |
|
|
![]()
Diffusion : diffusion Lambertienne
La couleur d’un objet est directement issue de la quantité de lumière qui le touche et des caractéristiques physiques de l’objet vis à vis des longueurs d’onde qu’il diffuse.
Modèle de Lambert: La diffusion est effectuée isotropiquement (uniformément dans toutes les directions).
-> Il n’y a pas plus de lumière diffusée dans une direction que dans une autre.
-> Deux directions d’incidence différentes peuvent conduire à la même lumière diffusée (si l'angle d'incidence est égal pour les deux directions, voir plus loin).
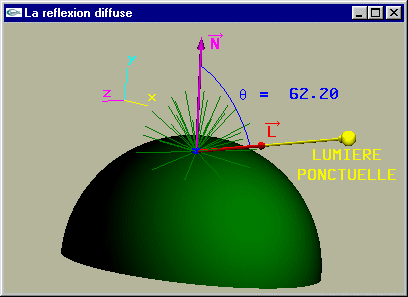
L’éclairage d’un point P d’une surface s dépend uniquement des caractéristiques matérielles de s et de l’angle q (angle
d'incidence) entre le vecteur normé
![]() vers la source de lumière en P et la normale
vers la source de lumière en P et la normale
![]() extérieure à s en P.
extérieure à s en P.
| Lumière diffusée |
|
|
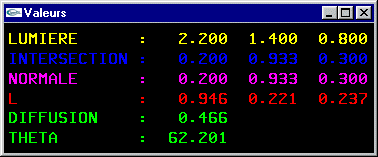
Cette valeur est donnée par la formule L = Ip Kd cos(q).
Ip est l’intensité de lumière (énergie lumineuse par unité de surface) reçue en P (proportionnelle à la quantité d'énergie émise par la source lumineuse, inversement proportionnelle au carré de la distance entre P et la source lumineuse) et Kd est le coefficient de diffusion de la surface (compris entre 0.0 et 1.0).
L'utilisation de cos(q) caractérise mathématiquement le fait que plus la lumière est zénithale (q tend vers 0.0°), plus elle éclaire fortement une surface. Au contraire, plus la lumière est rasante (q tend vers 90.0°), moins elle éclaire cette même surface.
Autre formulation (sans cosinus et sans angle) : L = Ip Kd (![]() .
.![]() )
)
Si le produit scalaire donne une valeur négative le point P est masqué par la surface à laquelle il appartient et n'est donc pas éclairé. Dans ce cas L = 0.0.
Une autre interprétation consiste à dire que, dans cette situation, la source lumineuse est sous l'horizon constitué par la surface elle-même.
On peut calculer la luminosité de tout objet en chacun de ses points.
A partir de cette luminosité et d'une teinte intrinsèque on calcule la couleur en chaque point (compte non tenu des composantes de lumière réfléchie spéculairement
et transmise).
Plus précisément, l'attribution à l'objet (à la surface de l'ojet) de coefficients de diffusion dans le rouge, vert et le bleu (teintes de base en synthèse additive) permet de modéliser
la couleur "intrinséque" de l'objet par les longueurs d'onde qu'il diffuse.
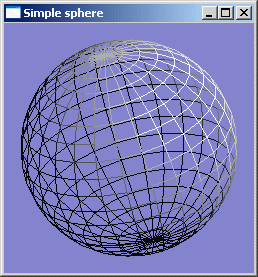
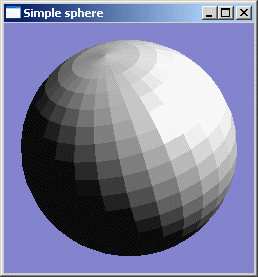
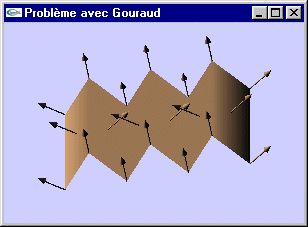
Problème: Dans le cas d’un objet représenté par facettes planes, chaque facette aura une normale donc une illumination et donc finalement une couleur constante.
-> Le passage d'une facette à une autre est très visible.
| Visualisation des facettes en cas d'ombrage plat |
|
|
![]()
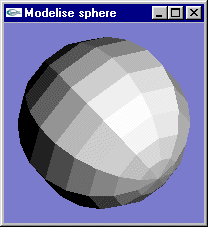
Le calcul d'illumination de Gouraud (illumination par interpolation de couleurs) permet de masquer le passage brusque d'une couleur à une autre lors du passage d'une facette plane à une facette plane voisine sur un objet courbe modélisé par un ensemble de facettes planes adjacentes.
Soit un objet modélisé par un ensemble de facettes triangulaires adjacentes (connexes).
Chaque facette est munie de trois couleurs: une pour chacun de ses sommets.
Un sommet adjacent à plusieurs facettes se voit attribué une seule couleur. Celle-ci est donc commune pour ce sommet pour toutes les facettes qui le réfèrent.
On attribue une couleur à chacun des pixels interne à la facette par double interpolation linéaire (interpolation bilinéaire) entre ces trois couleurs.
Interpolation bilinéaire
Problème : Calculer la couleur de chacun des sommets de chacune des facettes.
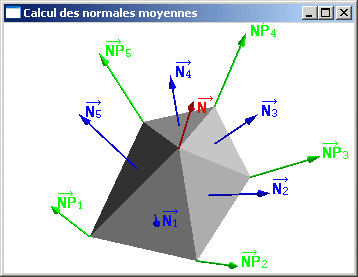
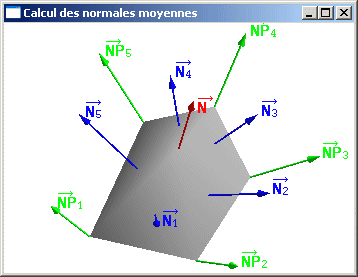
Soit en chaque sommet s le vecteur moyen
![]() égal à
égal à
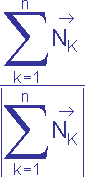 où les n vecteurs
où les n vecteurs
![]() sont les n vecteurs normaux aux facettes adjacentes à s. Cette normale moyenne caractérise assez bien l'orientation globale au niveau du sommet s (orientation globale des facettes adjacentes
à s).
sont les n vecteurs normaux aux facettes adjacentes à s. Cette normale moyenne caractérise assez bien l'orientation globale au niveau du sommet s (orientation globale des facettes adjacentes
à s).
Si on utilise Lambert, l'illumination en s est Ls = Ip Kd (![]() .
.![]() ) qui permet, en utilisant les
coefficients de diffusion, de calculer la couleur attribuée au sommet s pour toutes les facettes qui le partagent.
) qui permet, en utilisant les
coefficients de diffusion, de calculer la couleur attribuée au sommet s pour toutes les facettes qui le partagent.
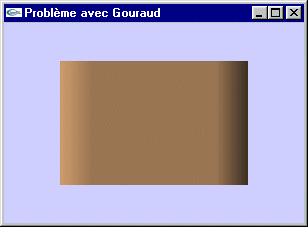
| Masquage des facettes par ombrage de Gouraud |
|
|
Caractéristiques
-
Technique efficace en terme de temps de calcul pour l'obtention d'un réalisme moyen.
| Ombrages lissé (Gouraud) et plat |
|
|
-
Implantation facile dans le cadre de la programmation de l'algorithme du Z-Buffer qui permet l'élimination des parties cachées.
-
L'utilisation d'une interpolation entre des valeurs numériques n'est qu'une approximation qui peut conduire à des défauts de visualisation.
| Problèmes liés au lissage de Gouraud |
|
|
-
Bon compromis entre vitesse et réalisme
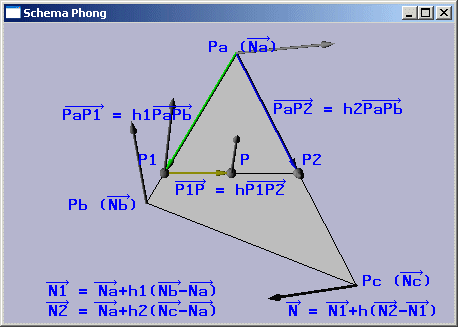
Principe: Réaliser le calcul d'illumination par interpolation directe à partir des normales associées aux sommets des facettes.
Pour chaque pixel, on aura une normale interpolée qui permettra le calcul de l'illumination en ce pixel par une formule donnant la quantité de lumière diffusée (Lambert).
Double interpolation linéaire sur les normales
Caractéristiques
La quantité de calcul nécessaire à une implémentation de l'algorithme de Phong est beaucoup plus importante que celle relative à l'emploi de Gouraud.
Les opérations effectuées agissent sur des réels et non sur des entiers.
-> Les temps de calcul sont plus longs.
Le modèle de Phong est plus réaliste que le modèle de Gouraud. Il permet de plus de palier les incompatibilités ou limitations inhérentes au modèle de Gouraud vis à vis de
certains phénomènes visuels (simulation de la réflexion spéculaire par exemple).
Il produit en effet une normale en chaque pixel, normale qui peut être employée pour des calculs visant à améliorer la qualité des images.
Lissage de Phong, vraies et fausse couleurs
Ombrage flat
Ombrage de Gouraud
Ombrage de Phong
En fausses couleurs
Les calculs d’illumination de Lambert, Gouraud et Phong sont basés sur une modélisation de la lumière diffusée. Ils ne permettent intrinsèquement pas de rendre la lumière réfléchie et la lumière transmise.
Toutefois, au prix d'approximations, ces phénomènes peuvent être visualisés (simulés).
On appelle réflexion spéculaire le phénomène de réflexion de la lumière dans un cône plus ou moins ouvert autour d'une direction privilégiée.
-> Visualisation des reflets des sources lumineuses
-> Aspect laqué
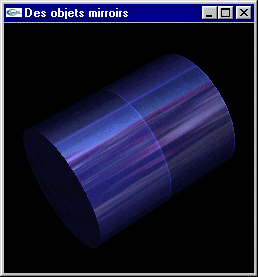
-> Aspect miroir si les objets sont assimilés à des sources lumineuses
A l'extrème, ce cône étant totalement fermé, la réflexion spéculaire est alors parfaite et ne s'effectue que selon l'axe privilégié (effet miroir parfait). On ne voit plus le reflet des sources lumineuses ponctuelles.
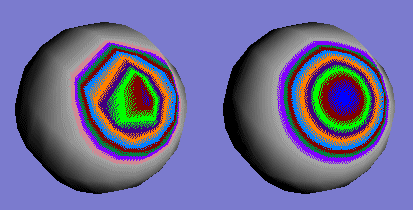
| Réflexions spéculaires sur une sphère |
|
|
La quantité de lumière réfléchie spéculairement est fonction de l'angle existant entre la direction privilégiée de réflexion et l'axe de vision de l'observateur. Plus cet angle est grand, moins il y a de lumière spéculaire. Si l'observateur change de position, les taches de lumière spéculaire changent de position et semblent le "suivre".
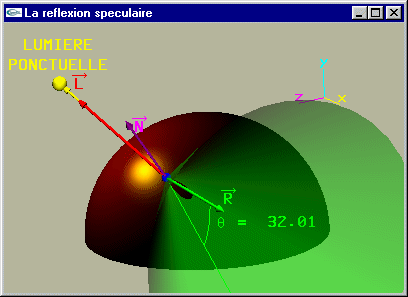
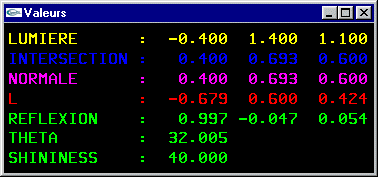
| Géométrie d'une tache de réflexion spéculaire |
|
|
L'apparition de taches de réflexion spéculaire est directement fonction de la position de l'observateur et est l'un des indices utilisés par le cerveau pour se faire une idée de la forme en 3D des objets.
La surface de l'objet où apparaît la lumière spéculaire prend généralement la couleur de la source lumineuse elle-même.
Transmission
Deux approches :
- Implantation des règles de l'optique géométrique (loi de Snell-Descarte)
-> déviation des rayons lumineux
-> déformation possible de la forme des objets vus à travers d'autres objets - Simple transparence sans déviation des rayons lumineux
-> pas de déformation
Problématique intimement lièe à l'algorithme de rendu utilisé
![]()
Modélisation de la lumière et des matériaux au sein des librairies 3D
Principes
Une modélisation complète des éclairages au sein d'une scène mettrait en oeuvre un grand nombre de phénomènes physiques qui reposent sur le déplacement de l'énergie lumineuse:
- réflexions diffuses,
- réflexions spéculaires,
- transmissions,
- sources lumineuses ponctuelles,
- sources lumineuses surfaciques,
- sources lumineuses volumiques,
- diffusion dans les matériaux,
- réflexions multiples et infinies,
- ...
-> Impossibilité de modéliser l'ensemble de ces phénomènes
-> Une grande difficulté pour gérer les éclairages avec pour résultat la réalité
Première typologie de modélisation des lumières : type de réponse générée
Les librairies 3D sont généralement axées sur la seule modélisation des réflexions diffuses et spéculaires vis à vis de sources lumineuses identifiées comme telles (en particulier à l'exclusion des objets eux-mêmes considérés en tant que sources lumineuses) et proposent généralement des approximations visant à représenter les autres phénomènes (éclairage ambiant, transparences, ...). Ces approximations permettent de faciliter la construction de l'éclairage des scènes.
Pour chaque objet, définition d'un "matériel" de surface autorisant l'interaction avec différents types de lumières :
-
Lumière ambiante : Lumière éclairant uniformément les objets depuis toutes les directions.
Les objets peuvent répondre à l'éclairage de une ou plusieurs lumières "ambiantes" via l'utilisation de coefficients de réflexion ambiante spécifiques.
La lumière ambiante sert généralement à modéliser le fait que, dans le monde réel, tous les objets d'une scène sont éclairés (possiblement légèrement) même s'ils ne sont pas directement éclairés par une source lumineuse (éclairage après réflexions infinies sur les autres objets de la scène). -
Lumière diffuse : Lumière utilisée uniquement pour les calculs de diffusion.
Les objets peuvent répondre à l'éclairage de une ou plusieurs lumières "diffuses" via l'utilisation de coefficients de réflexion diffuse spécifiques. -
Lumière spéculaire : Lumière utilisée uniquement pour les calculs de réflexion spéculaire.
Les objets peuvent répondre à l'éclairage de une ou plusieurs lumières "spéculaires" via l'utilisation de coefficients de réflexion spéculaire spécifiques et d'un coefficient de réflectivité.
Cas particulier : La lumière "émise" par le matériel
Les objets ne sont pas intrinsèquement émetteurs de lumière et n'éclairent donc pas les autres objets mais sont caractérisés par ce niveau minimum d'éclairage défini directement au sein du matériel
et qui éclaire uniformément l'objet.
La couleur en un point est la somme des couleurs (des éclairages) correspondant aux réponses aux lumières présentes dans la scène et de la lumière "émises" en ce point.
Seconde typologie de modélisation des lumières : caractéristiques géométriques d'émission
Les sources lumineuses peuvent adopter différentes caractéristiques géométriques quant à leur émission d'énergie.
Les trois principaux types de lumière sont :
- lumière ponctuelle,
- lumière directionnelle,
- lumière de type "spot".
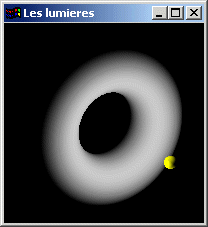
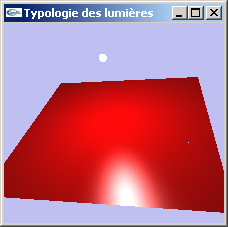
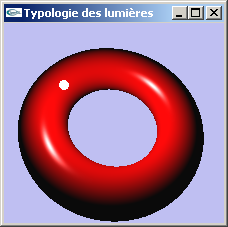
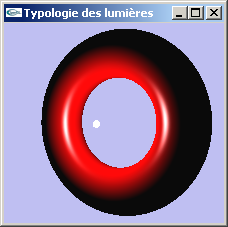
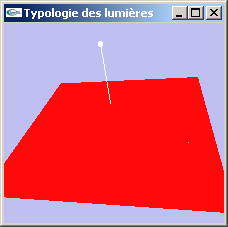
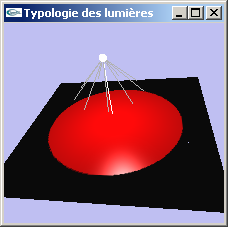
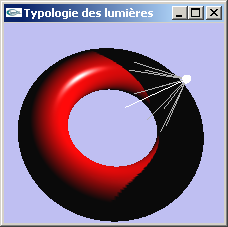
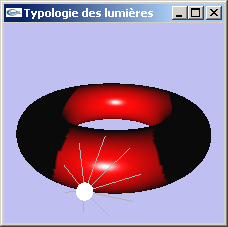
Lumière ponctuelle
Lumière placée en une position particulière et émettant dans toutes les directions depuis cette position.
En théorie, l'intensité de l'éclairage reçu est inversement proportionnelle au carré de la distance entre la source ponctuelle et le point qu'elle éclaire. Dans
la pratique, il peut ne pas y avoir d'atténuation (économie de temps de calcul et contrôle plus facile de l'éclairage car la décroissance quadratique est très rapide).
Exemple: Une ampoule
| Lumières ponctuelles |
|
|
|
|
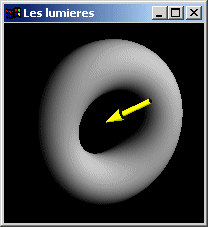
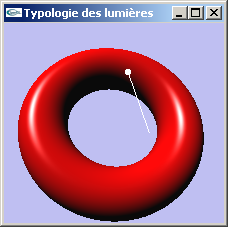
Lumière directionnelle
Lumière éclairant l'intégralité de la scène selon une direction d'éclairage uniforme.
L'intensité de l'éclairage est constante quelle que soit la position du point éclairé dans la scène.
Lumière assimilable à une lumière ponctuelle sans atténuation dont le point d'émission serait virtuellement placé à une distance infinie de la scène.
Exemple: Le soleil
| Lumières directionnelles |
|
|
|
|
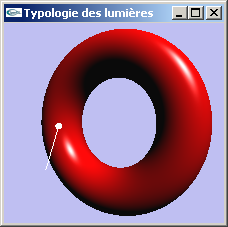
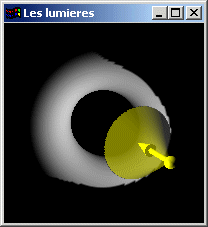
Spot
Lumière placée en une position particulière et émettant dans un cone orienté dans une direction particulière.
Le cone a son sommet placé au point d'émission du spot. Il est ouvert selon un angle plus ou moins important.
En théorie, l'intensité de l'éclairage est inversement proportionnelle au carré de la distance entre la source ponctuelle et le point qu'elle éclaire. Dans la pratique,
il peut ne pas y avoir d'atténuation (économie de temps de calcul et meilleur contrôle de l'éclairage). Il est souvent possible de gérer une atténuation de l'éclairage
vers les "bords" du spot.
Si les algorithmes d'élimination des parties cachées permettent la visualisation des objets en tenant compte du fait qu'ils peuvent se masquer les uns les autres, seules les techniques de calcul d'illumination permettent l'obtention d'un rendu réaliste.
Ces techniques permettent aussi de compenser partiellement certaines imperfections des modèles de conception 3D. On notera en particulier que la facettisation des objets modélisés par ensemble de facettes est masquable par la technique de Gouraud.
A minima les modèles d'illumination intègrent l'évaluation de la lumière diffuse. Ils peuvent intégrer en complément les aspects importants que sont les transparences (réfractions), les réflexions spéculaires et réflexions vis à vis d'objets non intrinsèquement lumineux. Ces phénomènes sont toutefois modélisés (souvent approximés voire très approximés) au prix de traitements demandant une quantité de calcul importante et présentent donc un temps global d'affichage allongé.
|
Réflexion d'images sur une surface |
|
|
|
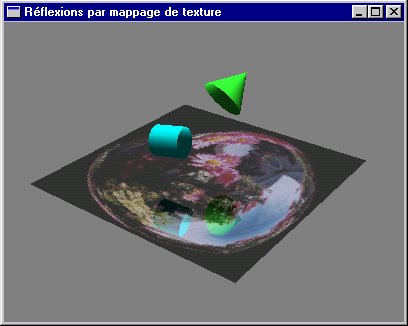
Réflexions par placage de texture |
|
|
|
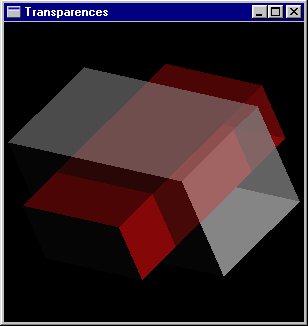
Transparences |
|
|
|
Flou de déplacement (Motion blur) |
|
|
|
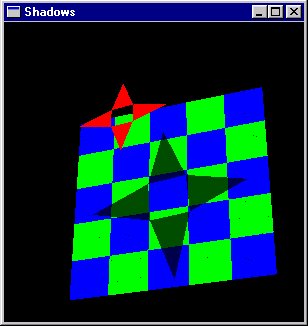
Des ombres portées |
|
|