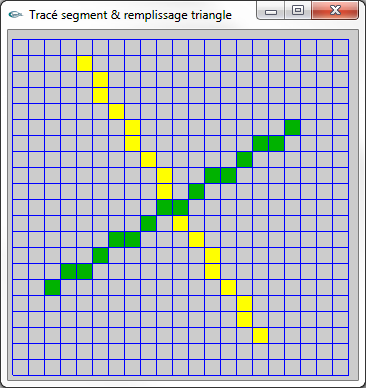
Figure (1) : Tracé des deux segments de droite
Commentaires
L'implantation de la fonction de tracé d'un segment de droite est la pure implantation de l'algorithme de Bresenham.
La fonction de rasterisation d'un triangle fait appel à la fonction auxiliaire cote destinée à
"rastériser" un coté. Cette fonction n'a pas pour but de faire quelque dessin que ce soit, mais plutôt de déterminer une abscisse x
pour chaque ordonnée y où au moins un pixel est à trouver sur le coté, ces abscisses étant destinées à servir d'abscisses extrêmes gauche ou
droite pour chaque trame horizontale de pixels du triangle. Cette fonction prend en paramètres les coordonnées des pixels initiaux et finaux du coté
ainsi qu'un tableau px destiné à recueillir les abscisses calculées. Les y peuvent directement servir d'indices dans ce tableau. Lorsque
plusieurs x sont trouvés pour le même y, c'est le dernier x trouvé dans le sens de parcours du coté qui est stocké dans px. L'implantation
de le fonction cote est basée en tout point sur l'algorithme de Bresenham sauf qu'au lieu d'allumer
des pixels, elle fait des écritures de valeurs d'abscisse dans px aux indices y.
La fonction triangle prend en paramètre, dans l'ordre, les coordonnées (x1,y1), (x2,y2) et (x3,y3)
des sommets P1, P2 et P3 définissant le triangle à rasteriser. Un point essentiel au bon fonctionnement de la fonction
triangle est que les 3 sommets P1, P2 et P3 doivent être triés par ordre d'ordonnées croissantes. La fonction
triangle débute par la déclaration des tableaux xg et xd destinés à recevoir les abscisses gauches et droites des trames
horizontales de remplissage du triangle. Ces tableaux sont définis de taille 4096, autorisant une résolution en y de 4096 pixels comptée des indices
0 (en bas) à 4095 (en haut). Ensuite, elle procède à la rasterisation dans les tableaux xg et xd des bords gauche et droit du triangle. Enfin, elle
trace effectivement les pixels en itérant sur y entre y1 et y3 inclus pour parcourir toutes les trames horizontales et, sur chaque trame, en itérant
entre xg[y] et xd[y] inclus pour allumer tous les pixels. La rasterisation des bords nécessite de déterminer pour chaque coté s'il fait partie
du bord droit ou du bord gauche. On sait que le coté P1‑P3 constitue à lui tout seul soit le bord droit soit le bord gauche et que P1‑P2
et P2‑P3 constituent l'autre bord. La position du point P2 vis à vis de la droite sous-tendue par P1 et P3 permet d'arbitrer entre
les deux possibilités. Cette arbitrage est implanté en utilisant une propriété du produit vectoriel qui veut que l'orientation du vecteur produit
vectoriel de deux vecteurs change de sens lorsque l'angle 3D que présente ces deux vecteurs passe de moins à plus de 0° ou de plus à moins
de 0°. Si on calcule le produit vectoriel de P1‑P3 et de P1‑P2 (on ajoute aux coordonnées x et y une 3ème coordonnée z = 0.0), on obtient un
vecteur de coordonnées (x,y,z) avec x = 0.0 et y = 0.0. Le signe de z donne la position de P2 vis à vis de la droite sous-tendue
par P1 et P3, c'est à dire d'un coté ou de l'autre. Il est inutile de calculer x et y qui ne peuvent pas être différents de 0.0.
Remarque : L'implantation réalisée ignore un problème. En effet, si un coté de la facette est tel que plus d'un pixel existe sur certaines trames horizontales de pixels lors de sa rasterisation (coté tel que abs(dx) > abs(dy) c'est à dire coté tel que le coefficient directeur de la droite sous-tendue appartient à l'intervalle ]-1.0,1.0[), notre algorithme sélectionne sur chaque trame concernée le dernier des pixels concernés dans le sens du parcours de rasterisation. Cela signifie que, selon le sens de parcours du coté, le pixel sélectionné sera soit le plus à droite soit le plus à gauche de toute suite de pixels de mêmes coordonnées y. Ce problème ne peut pas être ignoré quand il arrive sur les sommets P1, P2 ou P3 car il peut entrainer le non dessin du pixel correspondant au sommet, ce qui serait très visible (figure 8 ci-dessous). Une solution à ce problème particulier pourrait consister à rasteriser les cotés comme on l'a fait et à ajouter en fin de fonction cote les affectations px[yi] = xi et px[yf] = xf pour "forcer" à aller jusqu'aux extrémités. Une autre conséquence de ce problème est que le pixel sélectionné sera soit à l'intérieur ou soit à l'extérieur du triangle réel. Dans le premier cas, on ne tracera pas autant de pixels qu'il est possiblement souhaité, dans le second cas, à l'inverse, plus de pixels que possiblement souhaité seront tracés (figure (7) ci-dessous pour les deux cas). On peut envisager diverses solutions : (1) toujours parcourir les segments dans le même sens (sur la base d'un tri en y des sommets par exemple, c'est ce qui est implanté dans notre solution), (2) toujours sélectionner le pixel intérieur, (3) toujours sélectionner le pixel extérieur, (4) sélectionner le pixel à mi-distance entre le pixel intérieur et le pixel extérieur, etc. La seule solution qui ne convient pas est la (2) c'est à dire celle qui consiste à toujours sélectionner le pixel intérieur. La raison est que les facettes ne sont généralement pas utilisées individuellement, mais plutôt en ensemble de facettes adjacentes. Il est donc nécessaire que l'affichage de tels ensembles se fasse correctement, c'est à dire que le dessin de deux facettes adjacentes ne conduise pas à laisser des pixels ne pas être affichés à la frontière entre les deux facettes. Ce serait immanquablement le cas si la solution (2) était choisie car elle conduit à ne pas tracer tous les pixels sur les cotés.

Figure (1) : Tracé des deux segments de droite
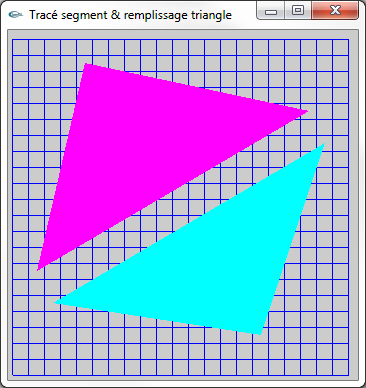

Figures (2) et (3) : Triangles rééls et rasterisés
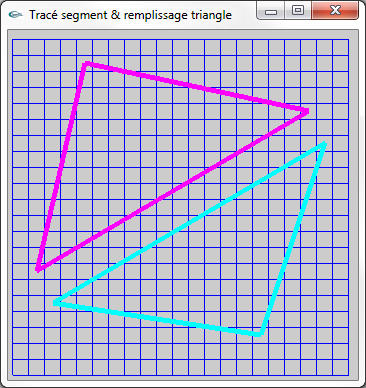

Figures (4) et (5) : Triangles dessinés par leurs cotés réels et rastérisés
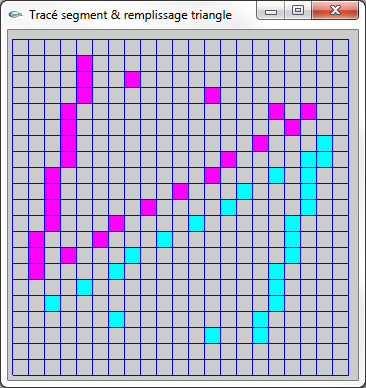
Figure (6) : Pixels extrèmes gauches et droits des trames horizontales des rectangles
-> derniers pixels sur la trame correspondant au bord dans le sens de son parcours de rasterisation
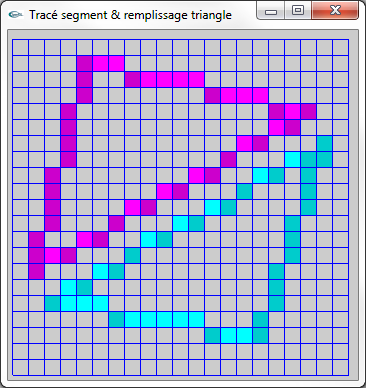
Figure (7) : Comparaison entre les pixels sélectionnés et les cotés rasterisés
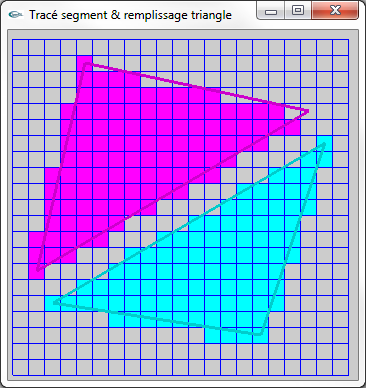
Figure (8) : Superposition des triangles réels dessinés par leurs bords et obtenus par rasterisation
Fichier source : RemplissageTriangle2D-1.cpp
/* Trace d'un segment de droite entre le pixel */
/* de coordonnees (xi,yi) et le pixel */
/* de coordonnees (xf,yf) au moyen de l'algorithme */
/* de Bresenham */
static void ligne(int xi,int yi,int xf,int yf) {
int x = xi;
int y = yi;
int dx = xf - xi;
int dy = yf - yi;
int xinc = ( dx > 0 ) ? 1 : -1;
int yinc = ( dy > 0 ) ? 1 : -1;
dx = abs(dx);
dy = abs(dy);
pixel(x,y);
if ( dx > dy ) {
int cumul = dx >> 1;
for ( int i = 1 ; i <= dx ; i++ ) {
x += xinc;
cumul += dy;
if ( cumul >= dx ) {
cumul -= dx;
y += yinc; }
pixel(x,y); } }
else {
int cumul = dy >> 1;
for ( int i = 1 ; i <= dy ; i++ ) {
y += yinc;
cumul += dx;
if ( cumul >= dy ) {
cumul -= dy;
x += xinc; }
pixel(x,y); } }
}
/* Rasterisation du cote de sommet initial (xi,yi) */
/* et de sommet final (xf,yf) en stockant */
/* dans le tableau px le dernier x */
/* calcule pour chaque y */
static void cote(int xi,int yi,int xf,int yf,int *px) {
int x = xi;
int y = yi;
int dx = xf - xi;
int dy = yf - yi;
int xinc = ( dx > 0 ) ? 1 : -1;
int yinc = ( dy > 0 ) ? 1 : -1;
dx = abs(dx);
dy = abs(dy);
px[y] = x;
if ( dx > dy ) {
int cumul = dx >> 1;
for ( int i = 1 ; i <= dx ; i++ ) {
x += xinc;
cumul += dy;
if ( cumul >= dx ) {
cumul -= dx;
y += yinc; }
px[y] = x; } }
else {
int cumul = dy >> 1;
for ( int i = 1 ; i <= dy ; i++ ) {
y += yinc;
cumul += dx;
if ( cumul >= dy ) {
cumul -= dy;
x += xinc; }
px[y] = x; } }
}
/* Rasterisation d'un triangle 2D */
/* Les coordonnees des trois sommets sont (x1,y1), */
/* (x2,y2) et (x3,y3) et doivent verifier y1<=y2<=y3. */
/* */
/* Solution imparfaite car ne gerant pas le probleme */
/* des cotes ou plus d'un pixel existe pour chaque y */
/* avec l'obligation de choisir un et un seul */
/* de ces pixels par y */
/* Consequences possibles : */
/* Non affichage des pixels correspondant aux sommets */
/* du triangle */
/* Non affichage sur les cotes de pixels qui auraient */
/* ete affiches si les cotes avaient ete rasterises */
/* par affichage de segments de droite rasterises. */
/* Apparition de trous entre deux facettes adjacentes */
/* car des pixels peuvent ne pas etre allumes */
/* a la limite entre les deux facettes car allumes */
/* pour aucune des deux facettes. */
static void triangle(int x1,int y1,int x2,int y2,int x3,int y3) {
int xd[4096];
int xg[4096];
if ( (x2-x1)*(y3-y1)-(x3-x1)*(y2-y1) > 0 ) {
cote(x1,y1,x2,y2,xd);
cote(x2,y2,x3,y3,xd);
cote(x1,y1,x3,y3,xg); }
else {
cote(x1,y1,x2,y2,xg);
cote(x2,y2,x3,y3,xg);
cote(x1,y1,x3,y3,xd); }
for ( int y = y1 ; y <= y3 ; y++ ) {
for ( int x = xg[y] ; x <= xd[y] ; x++ ) {
pixel(x,y); } }
}