Sujets et Corrections
de TD et TP
![]()
TD n°1
Création de scènes
en VRML 1.0
TD n°2 & 3
Premières scènes
OpenGL
TP n°1
Implantation
de fichiers VRML
Implantation
de programmes
OpenGL
TP n°2
Premières scènes OpenGL
TD n°5
Modélisation
par facettes
en OpenGL
TP n°3-4
Matériaux
et lumières
en OpenGL
TD n°6
Mathématiques
de l'infographie
TD n°7
Calculs d'illumination
Sur une facette
TP n°5
Mathématiques matricielles
TP n°6
Animation
et gestion
de la souris
TD n°8
Le clipping
de Cohen-Sutherland
TP n°7
Tracé de segment
Remplissage d'une facette traingulaire
TP n°8
Implantation
d'un programme
de rendu
par lancer de rayons
TP n°9
Plaçage de texture
bitmap 2D
Fichier
zip |
Dernière modification
30/11/10 09:19:39
TD n°1 : Création de scènes en VRML 1.0
(1) Programmer en VRML la scène suivante sans utiliser le nœud
Separator ailleurs que pour le Separator d'encadrement global du fichier:
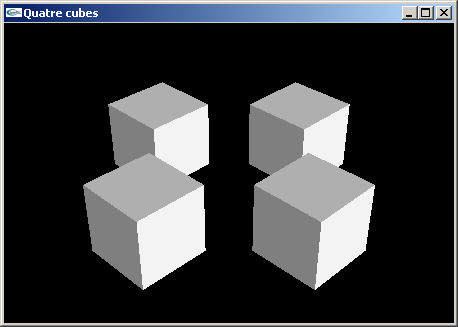
Quatre cubes de coté 2.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et
(-2.0,0.0,-2.0).

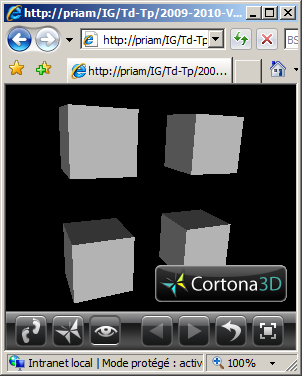
(2) Reprogrammer en VRML la scène de la question (1) de telle manière que les cubes aient une de leurs faces orientée vers l'origine du repère.

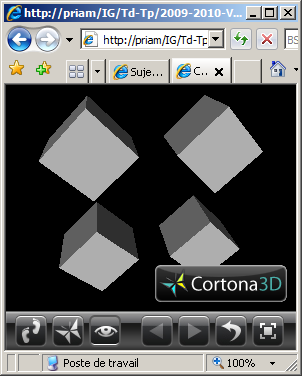
(3) Reprogrammer en VRML la scène de la question (2) en utilisant le nœud Separator pour rendre les objets indépendants les uns des autres et simplifier l'écriture du fichier scène.
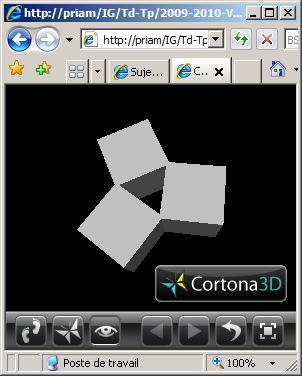
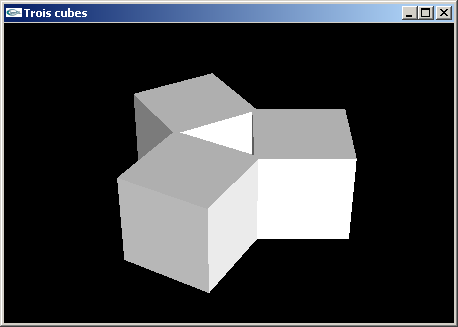
(4) Programmer une scène en VRML en plaçant 3 cubes de coté 2.0 aux 3 sommets d'un
triangle équilatéral défini avec les caractéristiques suivantes:
- rayon 1.5,
- centré sur l'origine,
- plongé dans le plan xOz.
Les 3 cubes présentent une de leurs faces orientée vers l'origine.
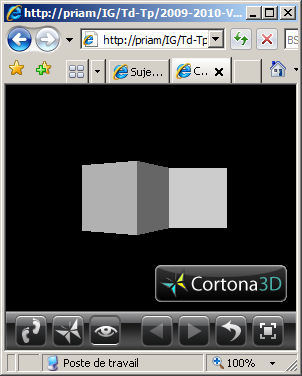
(5) Programmer la scène VRML modélisant un bras robot simplifié composé d'un
avant-bras et d'un bras.
L'avant-bras est articulé pour que sa base puisse tourner autour de l'axe Oy d'un angle
r1. Il s'agit d'un parallélépipède rectangle de dimension (3.0,1.0,1.0).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il
s'agit d'un parallélépipède rectangle de dimension (3.0,0.8,0.8).
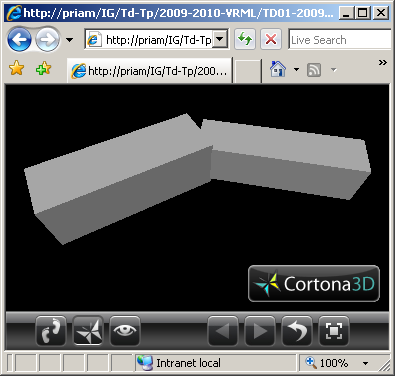
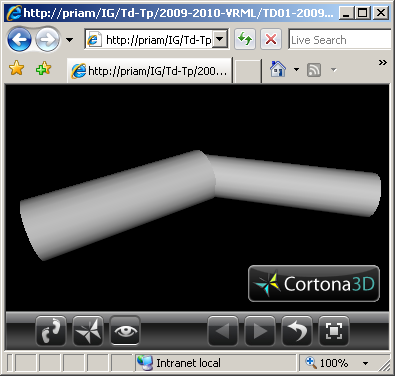
(6) Modifier le fichier VRML de l'exercice n°5 en remplaçant les parallélépipèdes par des cylindres de tailles équivalentes.
![]()
TD n°2-3: Premières scènes OpenGL
Exercice 1
Implanter en OpenGL les questions n°3 et n°4 du TD n°1.
Question n°3
Question n°4
Exercice 2
Implanter en OpenGL les questions n°5 et n°6 du TD n°1.

Question n°5

Question n°6
Exercice 3
a) Implanter en OpenGL une fonction de dessin d'une molécule de Benzène (C6H6).

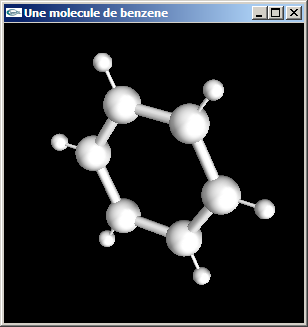
Les atomes de carbone (atome centraux) ont un rayon égal à 0.5.
Les liaisons entre 2 atomes de carbone ont pour longueur (centre à centre) 2.0 et pour
rayon 0.15.
Les atomes d'hydrogène ont un rayon égal à 0.25.
Les liaisons entre atome de carbone et d'hydrogène ont pour longueur (centre à centre)
1.2 et pour rayon 0.05.
La molécule est centrée sur l'origine et placée dans le plan xOy.
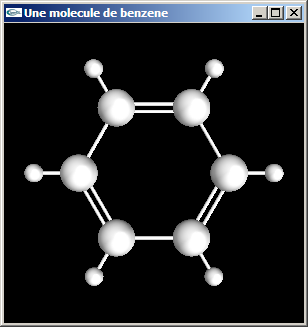
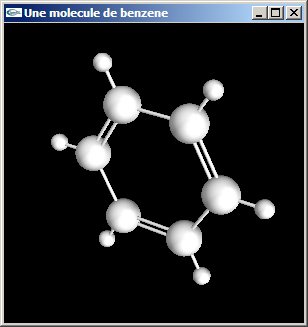
b) Modifier la modélisation de la molécule de benzène de la question précédente
pour que les liaisons carbone-carbone soient alternativement des liaisons simples et des
liaisons doubles (voir figure ci-dessous).
Les cylindres modélisant ces liaisons auront pour rayon 0.05 (comme les liaisons
carbone-hydrogène). Dans le cas des liaisons doubles, les deux cylindres de modélisation
seront écartés de 0.1.
Solutions
![]()
TP n°1 : Premières implantations en VRML et en OpenGL
Exercice n°1 (VRML)
Les viewers VRML disponibles sont:
- Un plugin Internet Explorer/Mozilla Firefox (Cortona Player)
- Une application de visualisation (Scene Viewer)
(a) Implanter les questions n°3 et n°4 du TD n°1.
(b) Implanter les questions n°5 et n°6 du TD n°1.
Exercice n°2 (OpenGL)
Création d'un projet Visual C++ permettant la compilation OpenGL:
- Les fichiers d'inclusion (nécessaires à la compilation) spécifiques à OpenGL sont GL/gl.h et GL/glu.h ainsi que GL/glut.h si GLUT est utilisé.
- Les librairies d'édition de liens (nécessaires à la création de l'exécutable) spécifiques à OpenGL sont OpenGL32.lib et glu32.lib ainsi que glut32.lib si GLUT est utilisé.
- Les dll (nécessaires à l'exécution) spécifiques à OpenGL sont OpenGL32.dll et glu32.dll ainsi que glut32.dll si GLUT est utilisé.
Si Visual Studio 2010 sous Windows est installé, l'utilisation des fichiers contenus dans l'archive IG.zip peut être nécessaire. Cette archive contient un répertoire "Include" contenant les fichiers .h d'OpenGL, un répertoire "Lib" contenant les fichiers .lib d'OpenGL en version Microsoft et Mesa3D ainsi que la dll glut32.dll nécessaire à l'exécution d'un programme 32 bits utilisant la librairie GLUT (les autres dll OpenGL sont préinstallées dans le système d'exploitation).
Si gcc sous Linux est utilisé, Mesa3D devrait avoir été installé au
cours de l'installation des outils de développement (gcc). S'il ne l'est pas, ou si l'on
constate l'absence de GLUT, ou si l'on souhaite utiliser une version plus récente que
celle disponible (en septembre 2009, la version la plus récente disponible de Mesa3D est
la version 7.5.1 qui est compatible OpenGL 2.1), il sera nécessaire de télécharger et d'installer (compilation puis
installation, une archive pour OpenGL, une archive pour GLUT et une archive pour des
exemples) la version souhaitée.
Pour l'édition de lien d'un exécutable OpenGL & GLUT, il est nécessaire de
spécifier les librairies GL, GLU et glut dans la ligne de commande de compilation.
(a) Télécharger le programme source exemple suivant : GetConfig20102011.cpp. Ce programme a
pour but d'initialiser OpenGL pour en extraire et afficher les informations de version.
Réaliser en la compilation et l'exécution.
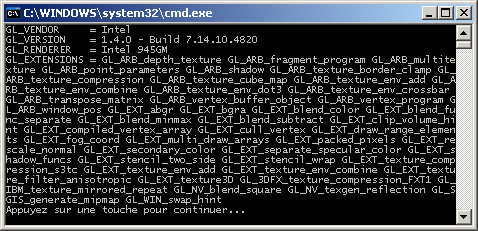
Exécutable compilé avec Visual C++ et
exécuté avec l'OpenGL du système d'exploitation
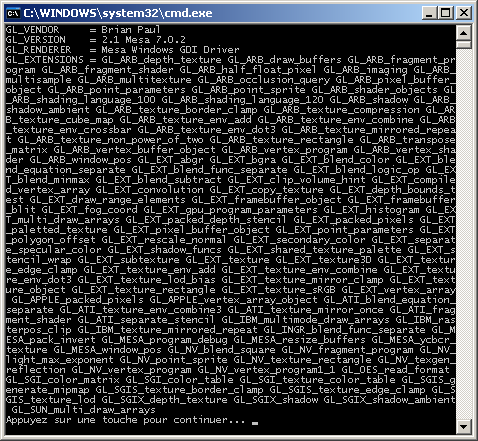
Exécutable compilé avec Visual C++ et
exécuté avec l'OpenGL Mesa3D version 7.0.2

Exécutable compilé avec Visual C++ et
exécuté avec l'OpenGL Mesa3D version 7.5.1
b) Recommencer la procédure de test avec le fichier source suivant: Animation2010-2011.cpp.
Ce programme utilise OpenGL et GLUt pour afficher une scène 3D simple avec animation,
matériel et lumières, caméra, ...
Cet exemple pourra être utilisé pour les TPs suivants comme base de travail et être
adapté à d'autres affichages.


![]()
TD n°4: Gestion des caméras
Exercice n°1: VRML
On considère la scène suivante obtenue par affichage du fichier VRML ci-dessous:
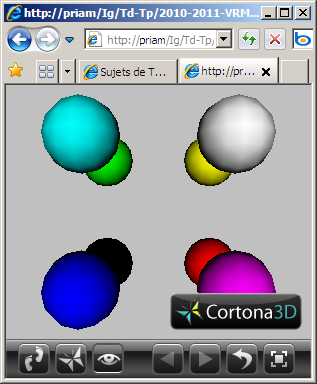
| #VRML V1.0 ascii Separator { Separator { Translation { translation 2.0 2.0 2.0 } Material { diffuseColor 1.0 1.0 1.0 } Sphere { } } Separator { Translation { translation 2.0 2.0 -2.0 } Material { diffuseColor 1.0 1.0 0.0 } Sphere { } } Separator { Translation { translation 2.0 -2.0 2.0 } Material { diffuseColor 1.0 0.0 1.0 } Sphere { } } Separator { Translation { translation 2.0 -2.0 -2.0 } Material { diffuseColor 1.0 0.0 0.0 } Sphere { } } Separator { Translation { translation -2.0 2.0 2.0 } Material { diffuseColor 0.0 1.0 1.0 } Sphere { } } Separator { Translation { translation -2.0 2.0 -2.0 } Material { diffuseColor 0.0 1.0 0.0 } Sphere { } } Separator { Translation { translation -2.0 -2.0 2.0 } Material { diffuseColor 0.0 0.0 1.0 } Sphere { } } Separator { Translation { translation -2.0 -2.0 -2.0 } Material { diffuseColor 0.0 0.0 0.0 } Sphere { } } } |
| TD04.wrl |
a) Inclure une caméra VRML réalisant une visualisation en projection en perspective de cette scène en gros plan depuis le point de coordonnées (0.0, 0.0, 150.0).
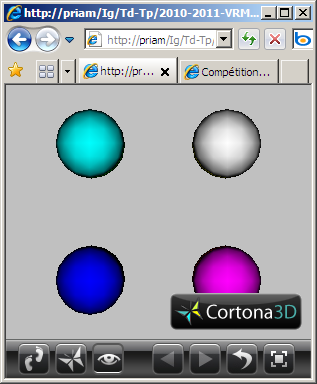
b) Inclure une caméra VRML réalisant une visualisation en projection en perspective de cette scène en gros plan depuis le point de coordonnées (0.0, 0.0, -20.0).

c) Inclure une caméra VRML réalisant une visualisation en projection en perspective de cette scène en gros plan depuis le point de coordonnées (0.0, 20.0, -20.0).
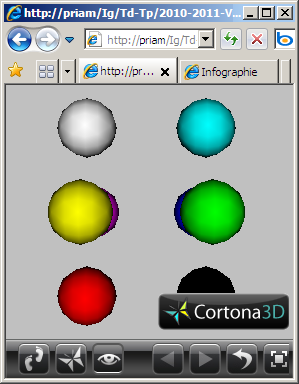
Solutions
Exercice n°2: OpenGL
La fonction scene OpenGL suivante dessine la même scène que le fichier VRML de l'exercice n°1.
static const float blanc[] = { 1.0F,1.0F,1.0F,1.0F };
static const float jaune[] = { 1.0F,1.0F,0.0F,1.0F };
static const float cyan[] = { 1.0F,0.0F,1.0F,1.0F };
static const float magenta[] = { 0.0F,1.0F,1.0F,1.0F };
static const float rouge[] = { 1.0F,0.0F,0.0F,1.0F };
static const float vert[] = { 0.0F,1.0F,0.0F,1.0F };
static const float bleu[] = { 0.0F,0.0F,1.0F,1.0F };
static const float noir[] = { 0.0F,0.0F,0.0F,1.0F };
void scene(void) {
glPushMatrix();
glPushMatrix();
glTranslatef(2.0F,2.0F,2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,blanc);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPushMatrix();
glTranslatef(2.0F,2.0F,-2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,jaune);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPushMatrix();
glTranslatef(2.0F,-2.0F,2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,cyan);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPushMatrix();
glTranslatef(2.0F,-2.0F,-2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,rouge);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPushMatrix();
glTranslatef(-2.0F,2.0F,2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,magenta);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPushMatrix();
glTranslatef(-2.0F,2.0F,-2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,vert);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPushMatrix();
glTranslatef(-2.0F,-2.0F,2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,bleu);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPushMatrix();
glTranslatef(-2.0F,-2.0F,-2.0F);
glMaterialfv(GL_FRONT,GL_DIFFUSE,noir);
glutSolidSphere(1.0,72,72);
glPopMatrix();
glPopMatrix();
}
|
a) La portion de code suivante réalise l'affichage de la scène précédente (width = largeur en pixels du viewport d'affichage, height = hauteur en pixels du viewport d'affichage).
glViewport(0,0,width,height); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluPerspective(...); glMatrixMode(GL_MODELVIEW) ; glLoadIdentity() ; gluLookAt(...); scene(); |
Compléter les appels de fonction gluPerspective et gluLookAt pour réaliser le même point de vue que la question a) de l'exercice n°1.

b) Compléter les appels de fonction gluPerspective et gluLookAt pour réaliser le même point de vue que la question b) de l'exercice n°1.
c) Compléter les appels de fonction gluPerspective et gluLookAt pour réaliser le même point de vue que la question c) de l'exercice n°1.

Solutions
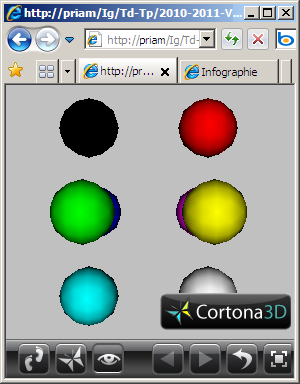
GLUT |
||
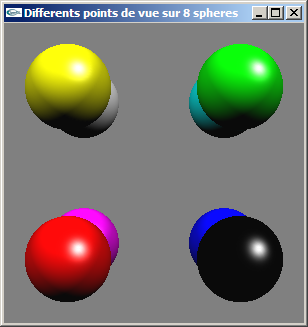
| Huit sphères | ||
![]()
TP n°2 : Premières scènes OpenGL
Spécifications de GLUt version 3
Exercice n°1
a) En adaptant le programme Animation2010-2011.cpp du TP n°1, implanter l'exercice du TD n°2 pour la modélisation et le dessin d'une molécule de benzène.

La fonction suivante pourra être utilisée pour modéliser un cylindre de hauteur h, de rayon r, de facteurs de facettisation n et m, centré sur l'origine et orienté selon l'axe y.
void cylindre(double h,double r,int n,int m) {
glPushMatrix();
glRotatef(90.0F,1.0F,0.0F,0.0F);
glTranslatef(0.0F,0.0F,-h/2);
GLUquadricObj *qobj = gluNewQuadric();
gluQuadricDrawStyle(qobj,GLU_FILL);
gluCylinder(qobj,r,r,h,n,m);
gluDeleteQuadric(qobj);
glPopMatrix();
}
b) Proposer et tester différentes alternatives permettant d'afficher la molécule en gros plan de manière à la visualiser avec précision.

Exercice n°2
a) Programmer la modélisation et l'affichage d'un tétraèdre modélisé par cylindres et sphères comme représenté sur la figure ci-dessous.
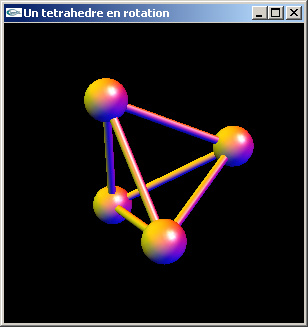
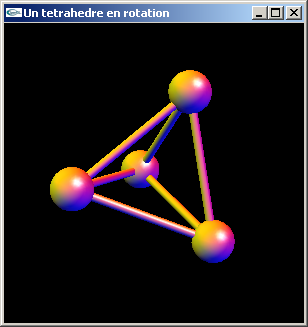
Les caractéristiques du tétraèdre sont les suivantes:
- Il est centré sur l'origine du repère.
- Une de ses faces est définie dans le plan xy.
- Ses sphères sont à une distance de sqrt(8.0) de l'origine.
- Ses sphères sont à une distance de sqrt(12.0) les unes des autres.
- L'une des sphères situées dans le plan xy est en position (2.0, 0.0,
-sqrt(0.5)).
- Les sphères ont pour rayon 0.5.
- Les cylindres ont pour rayon 0.1.
Solutions
GLUT |
||
| Benzène (question 1) | ||
| Benzène (question 1b version 1) | ||
| Benzène (question 1b version 2) | ||
| Benzène (question 1b version 3) | ||
| Tétraèdre | ||
![]()
TD n°5 : Modélisation par facettes en OpenGL
Exercice n°1
a) Modéliser par facettes un cube de coté 1.0 centré sur l'origine du repère de modélisation. On ne générera pas les normales.
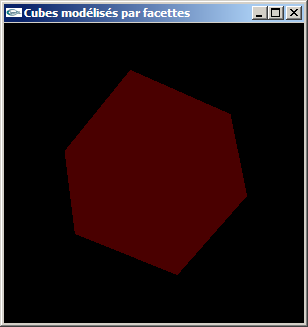
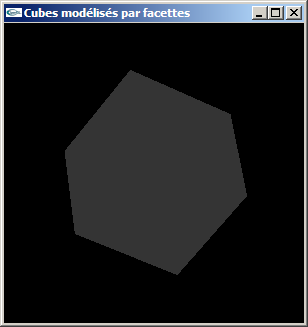
Lumières colorées et lumières blanches sur cubes sans normales
b) Modifier la modélisation de la question précédente pour ajouter la gestion des normales.

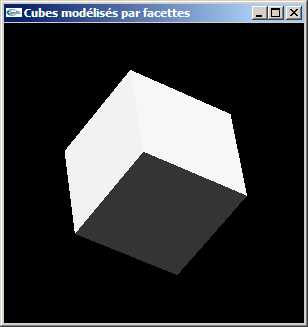
Lumières colorées et lumières blanches sur cubes avec normales
Modéliser par facettes un cylindre selon les caractéristiques suivantes:
- rayon 1.0,
- hauteur 2.0,
- centré sur l'origine du repère de modélisation,
- axé selon y,
- choix du nombre de facettes en découpage longitudinal,
- choix du nombre de facettes en découpage axial (y).
On ne modélisera pas les bases du cylindre, mais uniquement le tube.

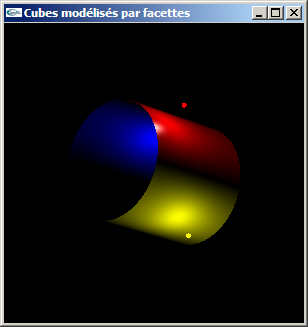
Cylindres par facettes
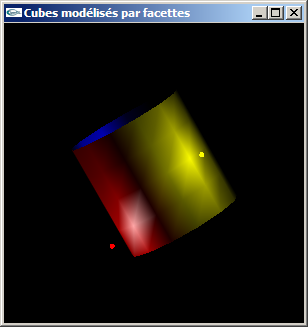
Cylindre par facettes (peu de facettes)
Solutions
![]()
TP n°3-4 : Modélisation par facettes - Matériaux et lumières en OpenGL - Animation
a) Implanter l'algorithme de modélisation de cylindre développé à l'exercice n°2 du TD n°5 pour dessiner un cylindre de rayon 1.0 et de hauteur 2.0.
b) Affecter un matériel au cylindre de la question a). Le matériel est configuré
avec les caractéristiques suivantes:
- pas de réflexion ambiante,
- pas d'émission,
- réflexion diffuse selon les coefficients (0.4, 0.4, 1.0),
- réflexion spéculaire selon les coefficients (0.6, 0.6, 0.0),
- réflectivité selon la valeur 64.0.
Ce cylindre est éclairé par une lumière directionnelle provenant de la direction 3/4 avant droite (1.0, 0.0, 1.0). Cette lumière est caractérisée par les valeurs (1.0, 1.0, 0.7) en diffusion et en spéculaire.
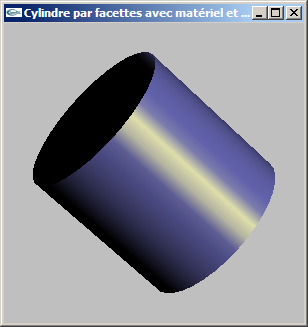
c) Modifier l'utilisation faite du matériel de la question b) pour qu'il devienne un matériel à deux faces. La face avant reste configurée avec les paramètres initiaux. La face arrière adoptera les coefficients (0.7, 0.7, 0.7) et (0.3, 0.3, 0.3) respectivement en diffusion et en spéculaire ainsi qu'une shininess de 110.0.
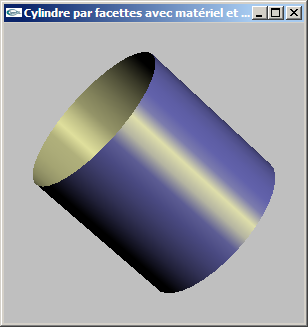
d) Modifier la lumière pour la transformer en une lumière ponctuelle placée en position (0.0, 0.0, 0.0).

e) Modifier une nouvelle fois la lumière pour la placer en position (1.0, 0.0, 1.0).
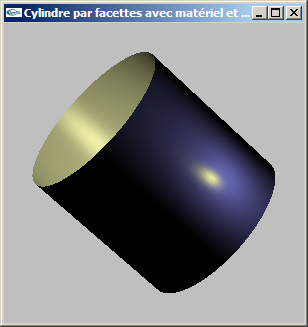
f) Modifier la lumière pour la transformer en un spot placé en position (2.0, 0.0, 2.0) ouvert de 10° et orienté vers l'origine du repère.
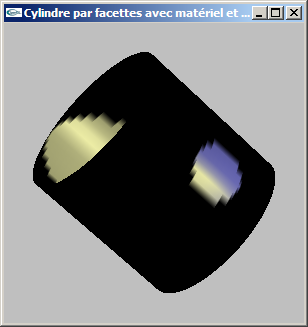
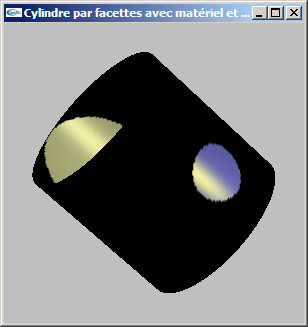
g) Modifier la lumière pour la transformer en une lumière ponctuelle initialement placée en position (2.0, 0.0, 2.0) se déplaçant par aller/retour sur la droite entre les positions (2.0, 0.0, 2.0) et (-2.0, 0.0, -2.0) à raison d'une distance de déplacement de 0.002828 (0.002*sqrt(2.0)) entre chaque image.
h) Modifier la lumière pour revenir au spot de la question f) et réaliser un déplacement circulaire de ce spot autour de l'axe Oy à raison de 0.1° de rotation entre chaque image tout en maintenant son orientation vers l'origine.
Solutions
GLUT |
||
| Cylindre par facettes avec éclairage sur matériel | ||
![]()
TD n°6 : Mathématiques de l'infographie
Exercice n°1
a) Développer une classe Position3D.
b) Développer une classe Direction3D.
c) Développer une classe FacetteTriangulaire.
d) Munir la classe FacetteTriangulaire d'une méthode de calcul de sa normale.
Exercice n°2
a) Développer une classe TransformationGeometrique.
b) Développer les classes Translation, Rotation et Scale.
c) Implanter une méthode "transformation d'une Position3D par une TransformationGeometrique". Implanter une méthode "transformation d'une Direction3D par une TransformationGeometrique".
d) Implanter une méthode "composition de 2 TransformationGeometrique".
Solutions
![]()
TD n°7 : Calculs d'illumination sur une facette
On utilisera les classes développées au TD n°6.
Exercice n°1
La quantité d'énergie reçue en un point P d'une surface est calculée par la formule
de Lambert :
L = Ip Kd (![]() .
.![]() ).
).
Ip est l’intensité de lumière (énergie lumineuse par
unité de surface) reçue en P (inversement proportionnelle au carré de la distance entre
P et la source lumineuse).
Kd est le coefficient de diffusion de la surface.
![]() est le vecteur normé de P vers la source de
lumière.
est le vecteur normé de P vers la source de
lumière.
![]() est la normale à la surface en P.
est la normale à la surface en P.
a) Développer les classes nécessaires à l'implantation de la formule de Lambert pour le calcul de l'éclairage sous lumière ponctuelle d'un point d'une facette triangulaire.
b) Implanter ce calcul.
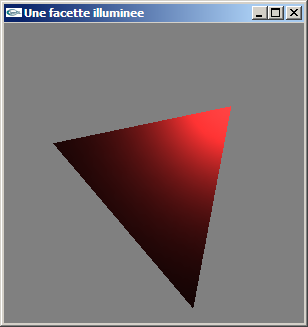
Exercice n°2
On s'intéresse à l'évaluation de la quantité de lumière réfléchie
spéculairement sur une facette triangulaire.
La méthode proposée consiste à calculer le cosinus de l'angle entre l'axe privilégié
de réflexion de la lumière de la source lumineuse au niveau de la position d'évaluation
P et la direction normée formée par le point P et la position de l'observateur. La
valeur obtenue, comprise entre -1.0 et 1.0, est seuillée à 0.0. A zéro, il n'y a pas de
réflexion spéculaire, à 1.0, la réflexion spéculaire est maximum.
La direction privilégiée de réflexion peut être calculée au moyen de
la formule suivante:
![]()
a) Implanter le calcul de la quantité de lumière réfléchie spéculairement en un point P d'une facette triangulaire éclairé par une source lumineuse ponctuelle.
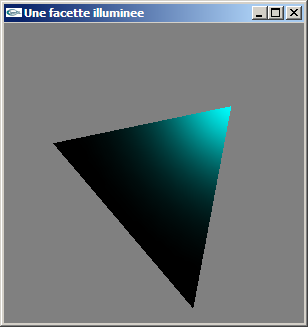
Solutions
| CoordonneesHomogenes.h | CoordonneesHomogenes.cpp | ||
| Position3D.h | Position3D.cpp | ||
| Direction3D.h | Direction3D.cpp | ||
| FacetteTriangulaire.h | FacetteTriangulaire.cpp | ||
| LumierePonctuelle.h | LumierePonctuelle.cpp | ||
| Couleur.h | Couleur.cpp | ||
| Energie.h | Energie.cpp | ||
| Test: Illuminations.cpp | |||
| Test avec affichage OpenGL: IlluminationsGL.cpp | |||
| Affichage d'une sphère: IlluminationsSphereGL.cpp | |||
![]()
TP n°5 : Mathématiques matricielles
Exercice n°1
a) Implanter la classe CoordonneesHomogenes du TD n°6.
b) Implanter la classe TransformationGeometrique du TD n°6.
c) Implanter les classes Position3D et Direction3D du TD n°6.
d) Implanter les classes Translation, Rotation et Scale du TD n°6.
Exercice n°2
a) Implanter et valider la composition de TransformationGeometrique.
b) Tester la non commutativité et l'associativité de la composition de TransformationGeometrique.
c) Implanter et valider la transformation d'une CoordonneesHomogenes par une TransformationGeometrique.
d) Tester l'associativité du produit matrice.matrice.vecteur.
Solutions
![]()
TP n°6 : Animation et gestion de la souris
Le fichier Scene.cpp (décrit par le fichier d'entête Scene.h) contient une fonction void scene(int l) de modélisation d'une scène composée d'une surface plane carrée de diagonale (-10.0, 0.0, -10.0) - (10.0, 0.0, 10.0) sur laquelle sont posés aléatoirement 100 "poteaux" parallélipipédiques. L'éclairage de cette scène est activé/désactivé par le paramètre "booléen" l.

a) Implanter le dessin de cette scène par une caméra de visualisation en perspective placée en position (0.0, 0.5, 0.0) orientée selon la direction de visualisation (0.0, 0.0, 1.0). L'ouverture verticale de la caméra est de 60°. Les plans cmin est cmax sont aux distances 0.1 et 100.0. La taille de la fenêtre d'affichage est 450 sur 200 pixels.
b) Modifier le programme précédent pour autoriser le déplacement de la caméra au moyen de la souris (avant-arrière) de manière à avancer ou reculer dans la scène dans l'axe de la caméra.
c) Modifier le programme précédent pour autoriser l'utilisation de la souris (droite-gauche) de manière à faire tourner la caméra vers la droite ou vers la gauche tout en continuant à pouvoir utiliser la souris pour avancer et reculer.
d) Modifier le programme précédent pour ajouter les contrôles clavier permettant de réaliser les mêmes mouvements qu'avec la souris, mais au moyen des touches de curseur up, down, left et right.
Solutions
![]()
TD n°8 : Le clipping de Cohen-Sutherland
Le TD est a réaliser au choix en C, en C++ ou en Java.
a) Suivant le langage choisi, définir et implanter les structures ou les classes nécessaires à l'implantation de l'algorithme de Cohen-Sutherland pour le clipping de segments à l'intérieur de rectangles à catés horizontaux.
b) Implanter une fonction de calcul du code de Cohen-Sutherland.
c) Implanter une fonction de calcul de l'intersection entre une droite quelconque et une doite horizontale ou verticale.
d) Implanter l'algorithme de Cohen-Sutherland.
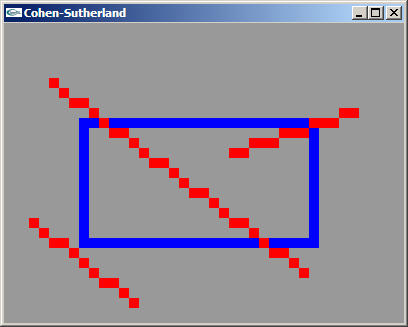
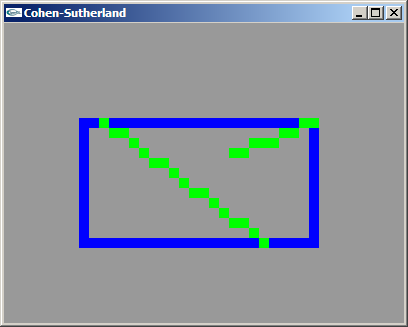
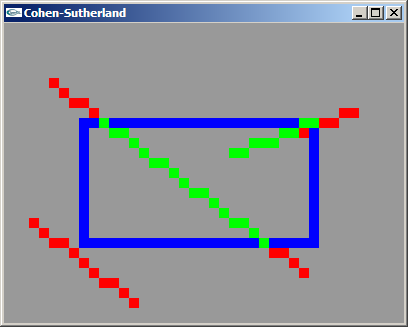
Solutions
| Position2D.h | Position2D.cpp | ||
| Segment2D.h | Segment2D.cpp | ||
| Rectangle2D.h | Rectangle2D.cpp | ||
| Trace.h | Trace.cpp | ||
| Clipping de Cohen-Sutherland | |||
![]()
TP n°7 : Tracé de segment par l'algorithme de Bresenham - Remplissage d'une facette triangulaire
On pourra exploiter la solution du TD n°8 pour gérer l'affichage écran de pixels en tant que carrés de 10 pixels de coté (fonction reshape et exécution de glPointSize(10.0F) dans la fonction init).
a) Implanter l'algorithme de tracé de segment par l'algorithme de Bresenham.

b) Implanter un algorithme de remplissage de facettes triangulaires 2D.
On recherchera les abscisses des pixels les plus à gauche et à droite de chaque ligne
horitontale de pixels intersectant le triangle. Ensuite, on pourra tracer une trame
horizontale entre ces deux abscisses pour l'ordonnée y de la ligne.
Pour cette recherche, on pourra utiliser une variante de l'algorithme de Bresenham
exécutée sur chacun des trois cotés de manière à rastériser ces bords.

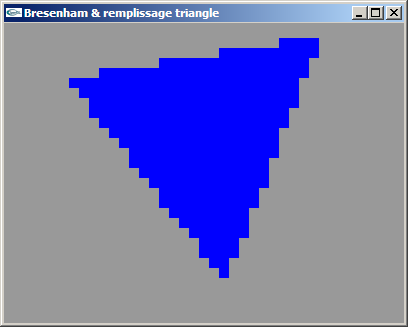
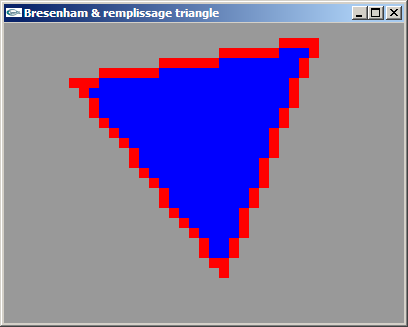
Solutions
| Position2D.h | Position2D.cpp | ||
| Segment2D.h | Segment2D.cpp | ||
| Triangle2D.h | Triangle2D.cpp | ||
| Trace.h | Trace.cpp | ||
| Tracé de segments - Remplissage triangle 2D | |||
![]()
TP n°8 : Implantation de la résolution de quelques problèmes mathématiques du lancer de rayons
Le fichier RayTracing.zip contient les fichiers code source d'un programme de rendu par lancer de rayons. Les scènes affichables au moyen de ce programme ne peuvent être composées que de sphères. Les sources lumineuses supportées sont de type ponctuelle et directionnelle.
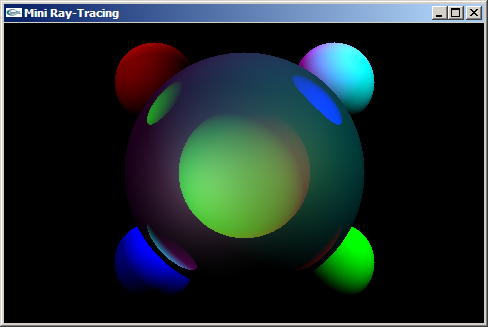
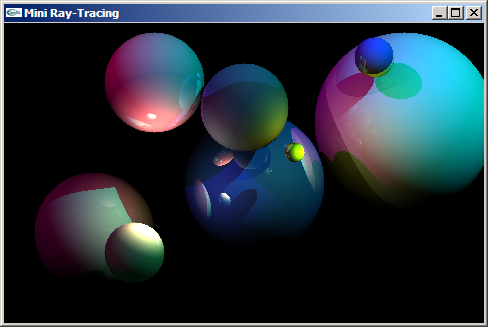
Dans ces fichiers sources, le corps de certaines méthodes n'a pas été implanté. Le travail demandé consiste à réaliser cette implantation. Ces méthodes sont:
- int Sphere::intersection(RayonLumineux *rl)
Teste s'il existe une intersection entre le rayon lumineux rl et une sphère.
Retourne un entier booléen indiquant s'il en existe au moins une.
- int Direction3D::reflexion(Direction3D *i,
Direction3D *n)
Calcule la direction du rayon réfléchi d'un rayon d'incidence de direction i au niveau d'un interface où la normale est de direction n.
Stocke le résultat dans this.
Retourne un entier booléen indiquant si le rayon réfléchi existe (si le rayon incident ne provient pas de sous l'interface).
- int Direction3D::transmission(Direction3D *i,
Direction3D *n,
double niSurNt)
Calcule la direction du rayon transmis à partir d'un rayon d'incidence de direction i au niveau d'une interface où la normale est de direction n. Le rapport ni/nt entre les coefficients de réfraction des milieux d'incidence et de transmission est niSurNt.
Stocke le résultat dans this.
Retourne un entier booléen indiquant si le rayon transmis existe (si la loi de Snell admet une solution).
- void Energie::calculDiffusion(Position3D *p,
Direction3D *n,
Couleur *kd,
LumierePonctuelle *lp)
Calcule l'énergie diffusée au point p d'une surface de normale n en p, munie des coefficients de diffusion kd, éclairée par la source lumineuse ponctuelle lp.
Stocke le résultat dans this.
- void Energie::calculDiffusion(Direction3D *n,
Couleur *kd,
LumiereDirectionnelle *ld)
Calcule l'énergie diffusée en un point d'une surface où la normale est n, munie des coefficients de diffusion kd, éclairée par la source lumineuse directionnelle ld.
Stocke le résultat dans this.
GLUT |
|
| RayTracing |
![]()
TP n°9 : Plaçage de texture 2D bitmap
La portion de code suivante crée un tableau d'octets représentatif d'une bitmap RGB de 8x8 pixels représentant un damier noir et blanc.
GLubyte *makeImage(void) {
GLubyte *tab =(GLubyte *) malloc(8*8*3*sizeof(GLubyte));
GLubyte *t = tab;
for ( int i = 0 ; i < 8 ; i++ )
for ( int j = 0 ; j < 8 ; j++ ) {
t[0] = t[1] = t[2] = ( (i+j)%2 ) ? 0x00 : 0xFF;
t += 3; }
return(tab);
}
a) Reprendre le cube modélisé par facettes lors du TD n°5 pour le texturer au moyen d'une image bitmap créée par cette fonction.

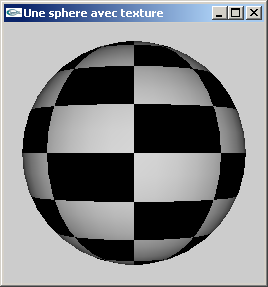
b) La fonction suivante peut être utilisée pour modéliser par facettes une sphère:
#ifndef M_PI
#define M_PI 3.14159265358979323846264338327950288
#endif
void solidSphere(float rayon,int nlat,int nlon) {
for ( int i = 0 ; i < nlat ; i++ ) {
float a1 = -M_PI/2.0F + i*M_PI/nlat ;
float a2 = a1 + M_PI/nlat ;
float cs1 = cos(a1);
float cs2 = cos(a2);
float sn1 = sin(a1);
float sn2 = sin(a2);
glBegin(GL_QUAD_STRIP);
for ( int j = 0 ; j <= nlon ; j++ ) {
float a = j*2*M_PI/nlon;
float cs = cos(a);
float sn = sin(a);
float x1 = cs1*cs;
float z1 = cs1*sn;
float x2 = cs2*cs;
float z2 = cs2*sn;
glNormal3f(x1,sn1,z1);
glVertex3f(rayon*x1,rayon*sn1,rayon*z1);
glNormal3f(x2,sn2,z2);
glVertex3f(rayon*x2,rayon*sn2,rayon*z2); }
glEnd(); }
}
Adapter cette fonction pour qu'elle intègre la création des coordonnées de texturage de manière à autoriser l'emploi de textures.
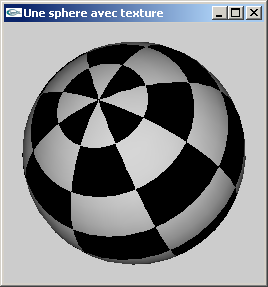
c) Les trois fichiers suivants:
sont des fichiers au format raw (RGB entrelacé, 1 octet par composante de couleur, le nom du fichier indique la résolution).

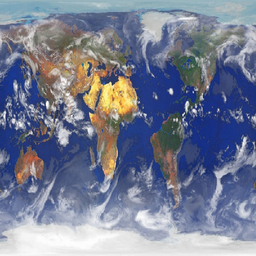

Développer une fonction de chargement d'un tel fichier en mémoire.
Adapter le code source des questions a) et b) pour afficher le cube texturé avec l'image
contenue dans le fichier Image-256-256.raw
et la sphère texturée avec, au choix, soit l'image du fichier Terre-256-256.raw, soit celle du fichier Mars-256-128.raw.

Solutions
GLUt |
||
| Texturage d'un cube avec un damier | ||
| Texturage d'une sphère avec un damier | ||
| Texturage d'un cube avec un fichier raw | ||
| Texturage d'une sphère avec un fichier raw | ||
![]()