Semestre 2 ST
Les matrices de variables, applications pratiques
| Cours | TD | TP |
![]()
| Problématique | Déclaration | Matrices en Mathématiques | Matrices en Physique | Matrices en Informatique |
![]()
![]()
![]()
- Emploi de "matrices" de variables dans le cadre de nombreux problèmes
- Matrice: Tableau à deux indices
Déclaration de tableaux à deux indices en langage algorithmique et en langage Java
- Chapitre "Tableaux de variables" pour la syntaxe en langage algorithmique ainsi que pour la syntaxe en langage Java.
Matrices pour les Mathématiques
-
Matrice: Tableau de variables à deux indices
- Composantes du même type
- Premier indice: Numéro de ligne
- Second indice: Numéro de colonne
| x | x | x | x | x |
| x | x | x | x | x |
| x | x | x | x | x |
nombre lignes = 3, nombre colonnes = 5
-
Vecteur: Tableau de variables à deux indices dont l'une des 2 tailles est égale à 1
- Matrice n*1
- Matrice 1*n
nombre lignes = 3, nombre colonnes = 1 |
nombre lignes = 1, nombre colonnes = 5 |
-
Matrices et vecteurs: "Objets" mathématiques de même catégorie: Tableau à 2 dimensions
-
Si tailles compatibles, objets associables au moyen d'opérations matricielles:
- Addition
- Soustraction
- Multiplication (composition)
-
Si tailles compatibles, objets associables au moyen d'opérations matricielles:
-
En programmation informatique, vecteur usuellement géré de manière simplifiée en utilisant un tableau à une dimension
-> Pas de second indice toujours égal à 0 à "traîner"
- Matrice carrée: Matrice avec des nombres de lignes et de colonnes identiques
-
En mathématiques utilisation fréquente des notions de matrice et de vecteur:
- Ensemble de valeurs: Un tableau unidimensionnel de taille arbitraire
- Position dans un espace: Un tableau unidimentionnel de taille égale à la dimension de l'espace
- Transformation géométrique: Un tableau bidimentionnel carré de taille égale à la dimension de l'espace
- Equation linéaire: Un tableau unidimentionnel de taille égale au nombre de variables de l'équation linéaire + 1
-
Système d'équations linéaires: Tableau bidimentionnel de taille ne*nv + tableau unidimentionnel de taille ne
où ne = nombre d'équations et nv = nombre d'inconnues - ...
- Utilisation fréquente de matrices carrées
Exemples
- Mathématiques matricielles: Produit matrice par vecteur
-
On considère un vecteur
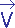 de taille n et une matrice carrée M de taille n*n.
de taille n et une matrice carrée M de taille n*n.
Le vecteur produit de M par
produit de M par 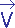 (noté
(noté  = M.
= M.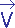 ) est calculé selon la formule:
) est calculé selon la formule:
wi = pour i de 1 à n
pour i de 1 à n
où les wi sont les composantes du vecteur , les mik
sont les composantes de la matrice M et les vk sont les composantes du vecteur
, les mik
sont les composantes de la matrice M et les vk sont les composantes du vecteur 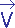 .
. -
Présentation intuitive du calcul du produit matrice-vecteur: La composante i du vecteur résultat est le produit de la ième ligne de la matrice par le vecteur
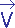 .
.
Exemple:
 .
. =
= 
|
constante N : entier <- ... |
|
/* Methode de calcul du produit d'un tableau */ |
|
ProduitMatriceVecteur.lda ProduitMatriceVecteur.java Exemple d'exécution |
- Mathématiques matricielles: Produit matrice par matrice
-
On considère une matrice M1 de taille n*m et une matrice M2 de taille m*p.
La matrice M produit de M1 par M2 (noté M = M1.M2) est une matrice de taille n*p et est calculée au moyen de la formule:
mij =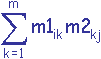 pour i de 1 à n et j de 1 à p
pour i de 1 à n et j de 1 à p
où les mij sont les composantes de la matrice M, les m1ik sont les composantes de la matrice M1 et les m2kj sont les composantes de la matrice M2. -
Présentation intuitive du calcul du produit matrice-matrice: La composante ij de la matrice résultat est le produit de la ième ligne de la première matrice par la jème colonne de la seconde matrice.
Exemple:
 .
.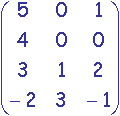 =
= 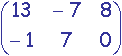
|
constante N : entier <- ... |
|
/* Methode de calcul du produit d'un tableau */ |
|
ProduitMatriceMatrice.lda ProduitMatriceMatrice.java Exemple d'exécution |
- Algèbre linéaire: Résolution d'un système de n équations linéaires à n inconnues
-
On considère le système de n équations linéaires à n inconnues:
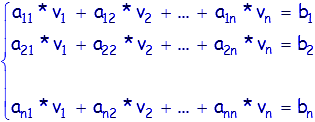
où les inconnues sont les vi et les constantes sont les aij et les bi. -
Présentation possible sous la forme matricielle A.V = B:
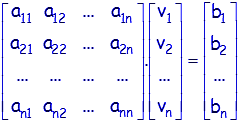
où A est une matrice carrée de taille n*n, V et B sont des vecteurs de taille n. -
Résolution de ce système:
- Détermination, s'il existe, du seul vecteur des vi qui vérifie l'ensemble de ces équations et donc du vecteur V qui vérifie le produit matriciel.
-
Exemples d'application pratique
- En deux dimensions: Trouver la position de l'intersection de deux droites
- En trois dimensions: Trouver la position de l'intersection entre une droite et un plan
- En dimension n avec n très grand (> 1000000): En informatique graphique, calculer l'éclairage d'une scène par radiosité
-
Méthode de résolution par pivot de Gauss
- Une première étape de transformation par "triangularisation":
- Transformation de la matrice A par traitement (substitution) de ses lignes de manière à remplir sa 1/2 matrice triangulaire inférieure stricte avec des 0.0
-
Transformation concourante du vecteur B pour que le système d'équations A.V = B reste équivalent
- n-1 itérations numérotées i consistant à soustraire à chaque ligne j à partir de la ligne i+1 le produit de la ligne i par le facteur fact tel que fact*m[i][i] = m[i][j] -> fact = m[i][j]/m[i][i]
-
Calcul de fact impossible si, lors d'une itération, m[i][i] = 0.0 (division par zéro)
-> Permutation la ligne i avec la première ligne k où m[k][i] est différent de 0.0
-> Si tous les m[k][i] égaux à 0.0 alors pas de solution unique (aucune solution ou une infinité de solutions)
Exemple:
Les matrices A et B sont 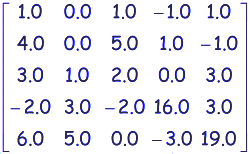 et
et  .
.
-
Etape n°1
-
Traitement de la ligne 2 par soustraction de 4.0 fois la ligne 1:
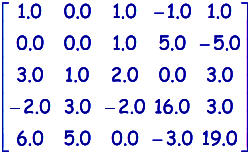 et
et 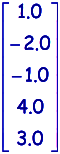 .
. -
Traitement de la ligne 3 par soustraction de 3.0 fois la ligne 1:
 et
et  .
. -
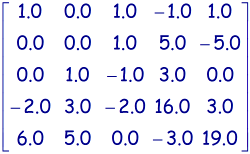
Traitement de la ligne 4 par soustraction de -2.0 fois la ligne 1:
 et
et  .
. -
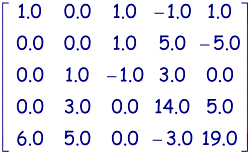
Traitement de la ligne 5 par soustraction de 6.0 fois la ligne 1:
 et
et  .
.
-
-
Etape n°2
-
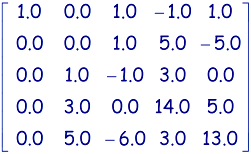
Permutation des lignes 2 et 3 car la composante d'indice (2,2) est égale à 0.0:
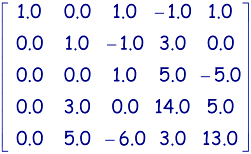 et
et  .
. -
Traitement des lignes 4 et 5:
 et
et  .
.
-
-
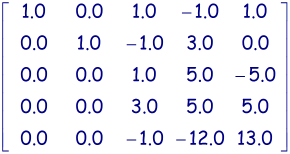
Etape n°3
-
Traitement des lignes 4 et 5:
 et
et  .
. -
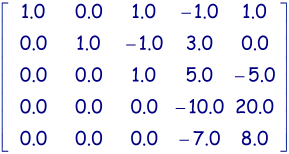
Etape n°4
-
Traitement de la ligne 5:
 et
et  .
.
-
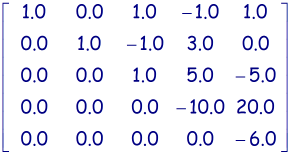
Une seconde (et dernière) étape: Calcul de V
-
vn d'ores et déjà calculable car sur la ligne n de la matrice A, il ne reste que des 0.0 sauf pour la dernière valeur d'indice
(n,n)
-> vn = bn/ann - Calcul de vn-1 possible car, vn étant connu, toutes les valeurs nécessaires à son calcul sont maintenant connues.
- Calcul de vn-2 possible car, vn et vn-1 étant connus, toutes les valeurs nécessaires à son calcul sont maintenant connues.
- Poursuite du calcul des v du calcul des vi jusqu'à v1.
-
vn d'ores et déjà calculable car sur la ligne n de la matrice A, il ne reste que des 0.0 sauf pour la dernière valeur d'indice
(n,n)
- v5 = -1.8/-6.0 = 0.3
- v4 = (24.0 - 20.0*0.3)/-10.0 = -1.8
- v3 = (-2.0 + 5.0*0.3 + 5.0*1.8)/1.0 = 8.5
- v2 = (-4.0 + 0.0*0.3 + 3.0*1.8 + 1.0*8.5)/1.0 = 9.9
- v1 = (1.0 - 1.0*0.3 - 1.0*1.8 - 1.0*8.5 + 0.0*9.9)/1.0 = -9.6
|
constante N : entier <- ... |
|
/* Methode de clonage d'un tableau */ |
|
PivotGauss.lda PivotGauss.java Exemple d'exécution |
- Large appel à l'informatique comme outil de simulation
-
Pourquoi simuler?
- Moins cher que les tests réels (crashs automobiles, analyses d'écoulements turbulents, ...)
- Réalisation de prévisions (météo, évolution climatique, collision de galaxies, ...)
- Analyse de phénomènes qu'il n'est pas possible de tester dans la réalité (essais nucléaires, formation des étoiles, super-novae, ...)
- ...
- Phénomènes à simuler fréquement décrits par des équations (continues ou non) pour lesquelles il n'existe pas de méthode de résolution analytique (i.e. pas de solution présentable sous la forme d'une formule simple, voire complexe)
-
Méthodes numériques de résolution de certaines classes de problèmes permettant de trouver une solution à partir d'une discrétisation du champ
de travail
- Champ unidimentionnel: Appel à des tableaux
- Champ bidimentionnel: Utilisation de matrices
- Dimension 3: Tableaux à 3 indices
Exemples
-
Propagation de la chaleur au sein d'une barre métallique
- Problème en dimension 1
- Décomposition (discrétisation) de la barre en une suite de morceaux pour chacun desquels la température est considérée uniforme
- Valeurs stockées et gérées dans un tableau à 1 indice
-
Augmentation du pas de discrétisation -> Obtention de résultats plus précis au prix d'un temps de calcul plus long
-
Propagation de la chaleur au sein d'une plaque métallique
- Problème en 2 dimensions
- Décomposition de la plaque en une grille de cellules pour chacune desquelles la température est considérée uniforme
- Valeurs stockées dans un tableau à 2 indices










Simulation de l'évolution de la température d'une plaque métallique sur laquelle
sont créés des points chauds
Exemple d'exécution
-
Simulation de la surface océanique
- Problème en 2 dimensions
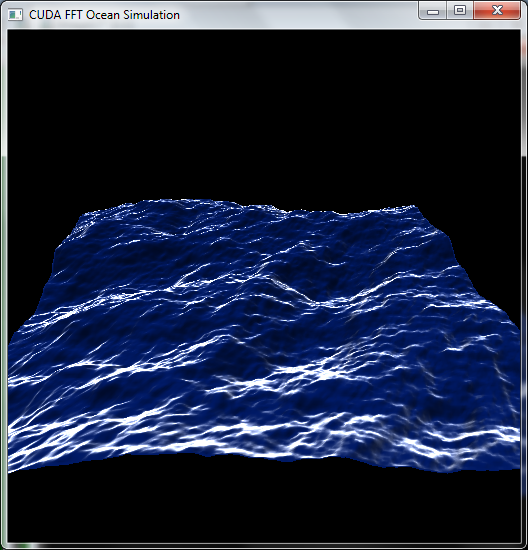
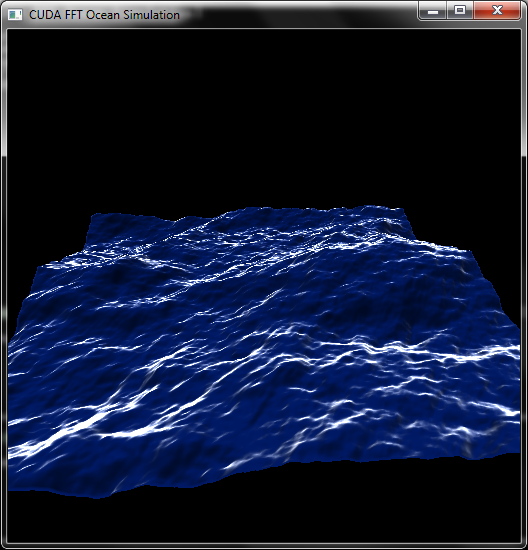
Simulation de surface océanique
Kit de développement CUDA (NVidia)
-
Evolution climatique
- Premiers modèles: Modèles en deux dimensions
- Surface de la Terre décomposée en longitude et en latitude en un maillage "carré"
- Informations relatives aux cellules de ce maillage stockées dans une matrice de variables
- Etude de l'évolution du climat en considérant chaque cellule comme une entité atomique de caractéristiques uniformes
- Modèles plus complexes: Trois dimensions
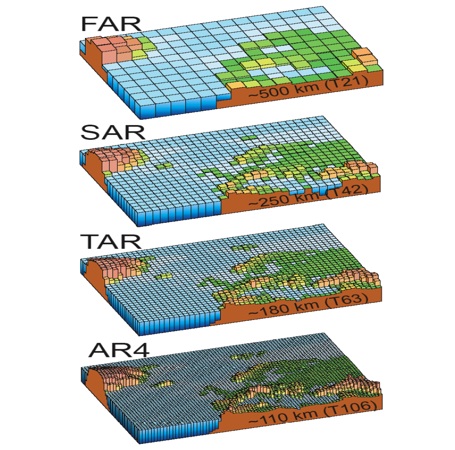
Décomposition de l'atmosphère en un maillage 2D
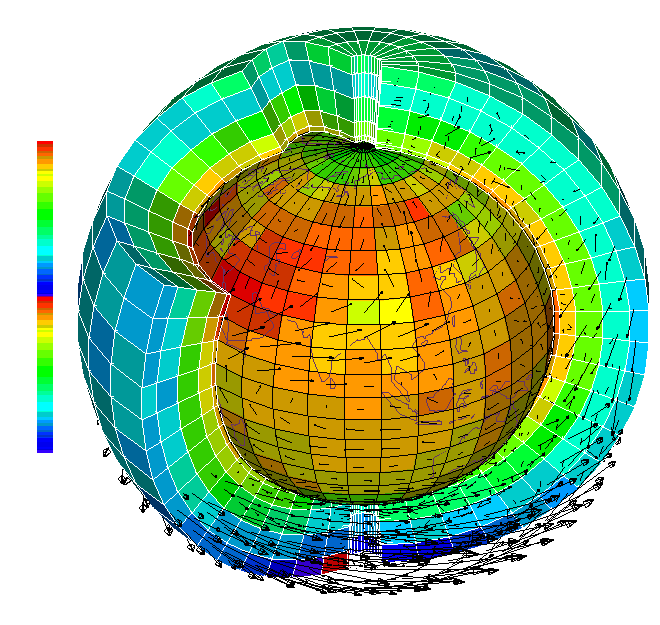
Décomposition de l'atmosphère en volumes élémentaires
-
Analyse des turbulences dans un fluide 2D
- Problème en deux dimensions
- Résolution des équations de mécanique des fluides (Navier-Stockes) complexe et extrêmement coûteuse en temps de calcul
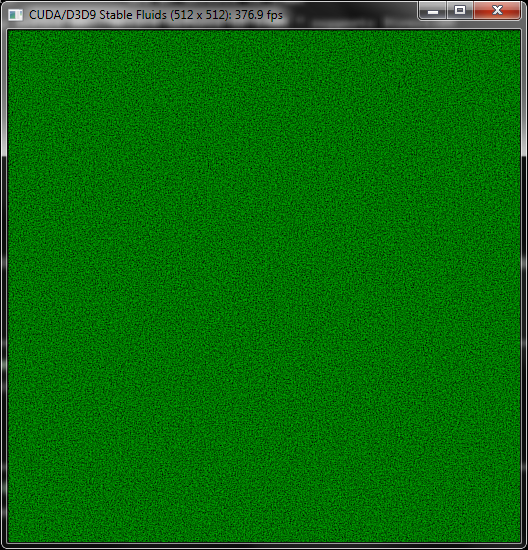

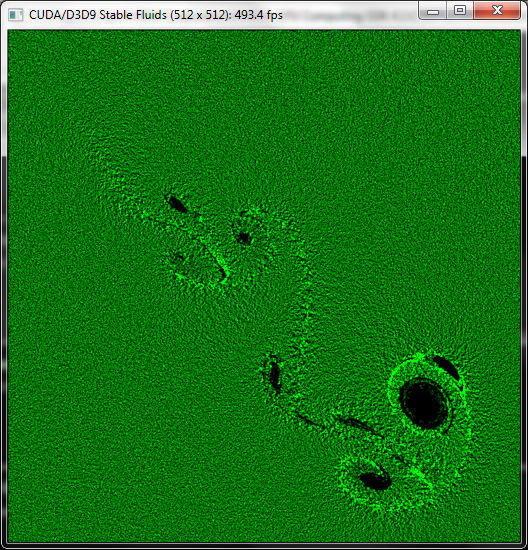
Simulation de fluides
Kit de développement CUDA (NVidia)
-
Analyse des turbulences sur une aile d'avion
- Problème en trois dimensions
- Résolution des équations de mécanique des fluides (Navier-Stockes)
- Historiquement, problème géré en dimension 2 avec simulation numérique sur des profils 2D de l'objet 3D
- Accroissement de la puissance des ordinateurs -> Passage en 3D avec une aile complète
- Bientôt possible de simuler l'écoulement sur un avion entier: ailes, fuselage, gouvernes, pylônes, réacteurs, ...
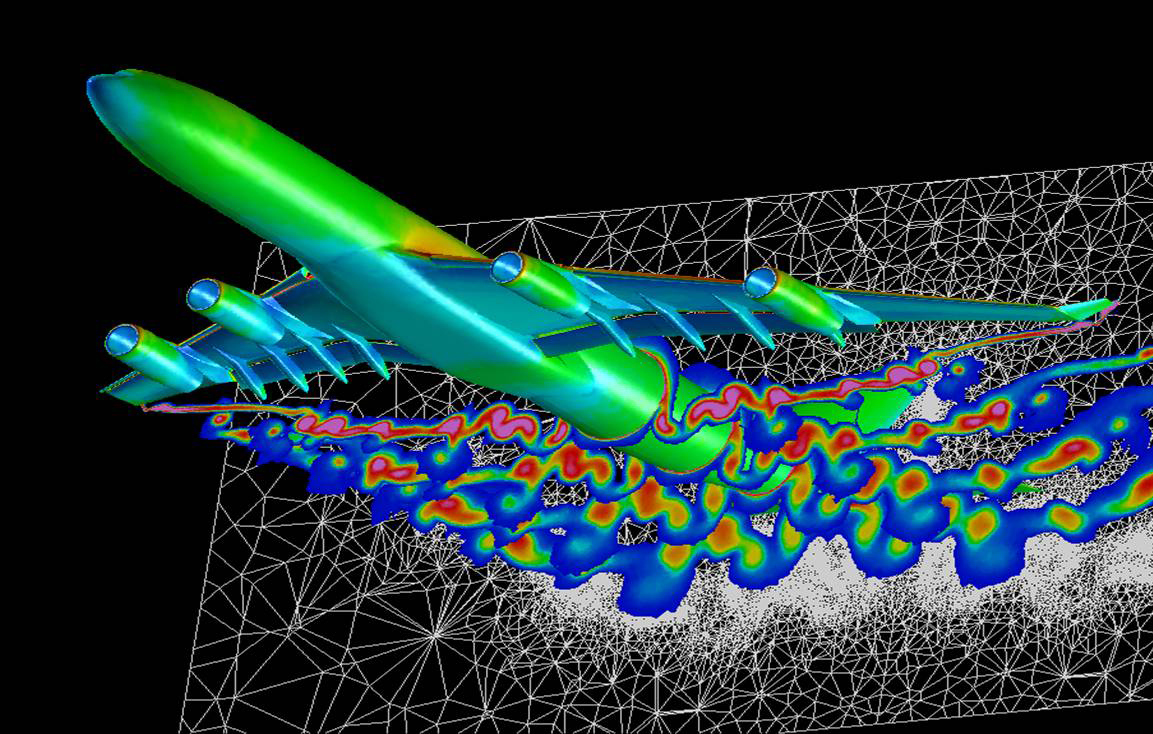
-
Problème des n-corps
- Comment évolue un système de n corps sous l'effet des forces de gravité qu'ils appliquent les uns sur les autres?
-
Pour n masses, 3*n équations différentielles du 2ème ordre
-> 6*n inconnues
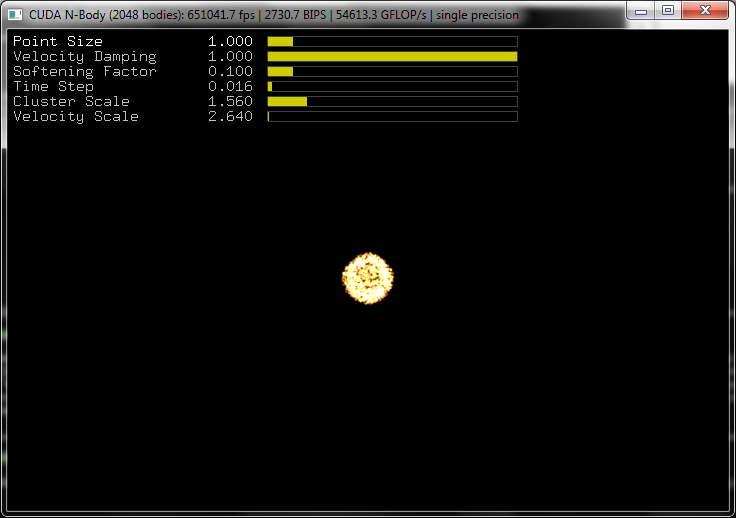
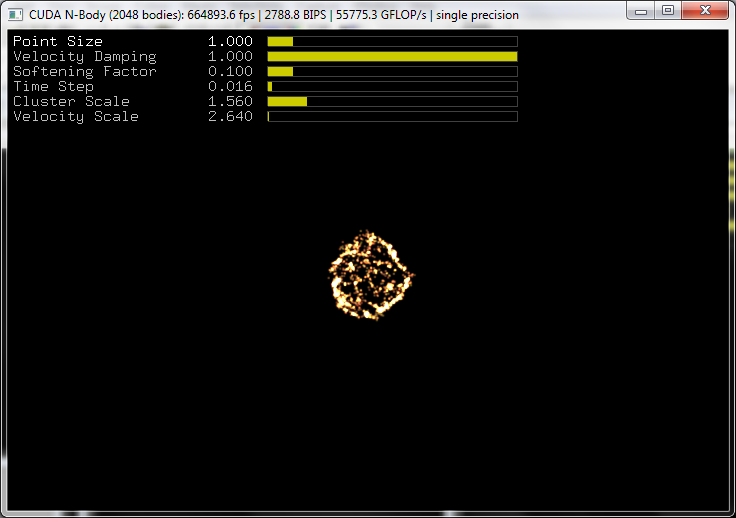
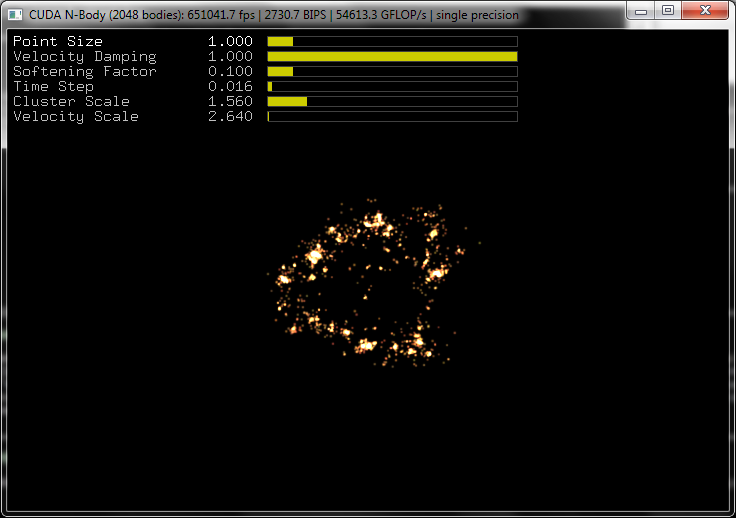
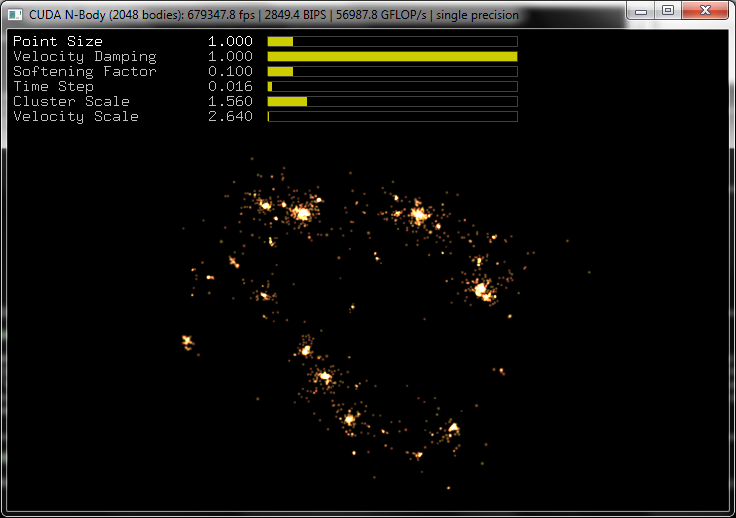
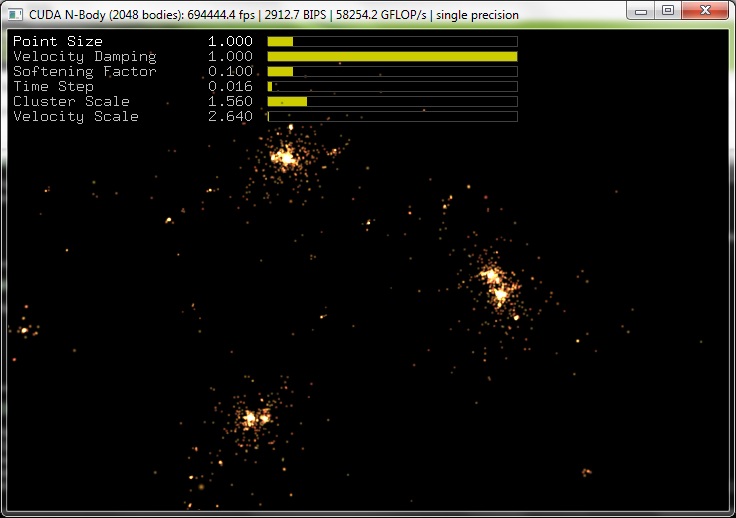
Résolution du problème des n-corps
Kit de développement CUDA (NVidia)

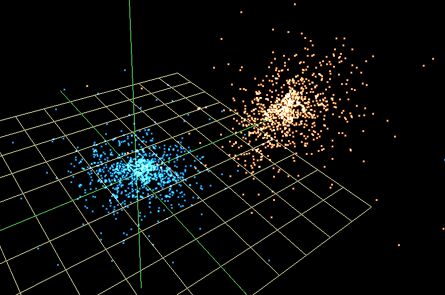
Simulations de collisions de galaxies
- Utilisation de matrices pour gérer les problèmes de l'informatique fondamentale qui se présentent naturellement sous forme 2D
Exemples
-
Les écrans d'ordinateur
-
Technologie "raster"

- Une grille rectangulaire de pixels carrés pour lesquels on peut choisir individuellement la couleur
- "Résolution": Nombres de colonnes et de lignes de pixels: 1024x768 -> 768 lignes de 1024 pixels
-
Autre caractéristique de la résolution: La "profondeur écran"
- Nombre de bits de données affectés au stockage de la couleur d'un pixel
-
En 24 bits (3 octets), répartition en trois "teintes de base" stockées individuellement sur 8 bits
-> 8 bits (1 octet) de composante rouge, 8 bits (1 octet) de composante verte et 8 bits (1 octet) de composante bleue
-> Définition de chaque composante au moyen d'une valeur entière positive codée sur un octet (dans l'intervalle [0,255])
-
Couleurs classiques:
- le noir (0,0,0)
- le blanc (255,255,255)
- le rouge saturé (255,0,0)
- le vert saturé (0,255,0)
- le bleu saturé (0,0,255)
- le jaune saturé (255,255,0)
- le cyan saturé (0,255,255)
- le magenta saturé (255,0,255)
-
Autres couleurs: Choix les valeurs "RVB" adéquates
-
Image affichée à l'écran: Une matrice de pixels codés en couleurs RVB stockée en mémoire
- Opération d'affichage de plus bas-niveau: "Allumer" un pixel avec une couleur particulière
- Autres opérations implantées en utilisant cette opération bas-niveau
-
Paramètres nécessaires à l'appel de fonction d'allumage de pixel:
- Position en x: un entier compris dans l'intervalle [0,rx-1] où rx est la résolution d'affichage en x
- Position en y: un entier compris dans l'intervalle [0,ry-1] où ry est la résolution d'affichage en y
-
Couleur d'affichage
-
"Librairie" de fonctions d'affichage graphique: Un grand nombre de fonctions de gestion de l'affichage en mode graphique et donc
d'écriture dans la matrice de pixels:
- Une ou plusieurs fonctions pour configurer la résolution d'affichage
- Une ou plusieurs fonctions pour afficher un pixel selon une couleur
-
D'autres fonctions d'affichage plus élaboré:
- Vidage la zone d'affichage avec une couleur (couleur de fond)
- Traçage de segments de droite
- Remplissage de polygones
- ...
-
Technologie "raster"
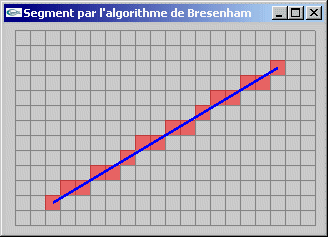
Dessin d'un segment de droite
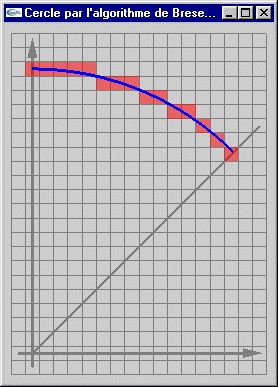
Dessin d'un arc de cercle

Remplissage d'une facette triangulaire
|
/** |
| Exemple d'affichage graphique bitmap |
-
Deux techniques de stockage d'images dans des fichiers:
- Vectoriel: Images stockées sous la forme d'objets graphiques de type segment de droite, rectangle, rectangle rempli, cercle, disque, ...
-
Bitmap: Images stockées sous la forme d'une grille rectangulaire de pixels décrits individuellement par une couleur
-
Déclinaison de ces techniques de diverses manières avec pour conséquence l'apparition de divers formats de fichiers:
- Exemples de formats vectoriels: Postscript (.ps) et SVG (.svg, Scalable Vector Graphic)
-
Exemples de formats bitmap: JPEG, BMP, GIF, PNG
- Compression ou non
- Si compression, perte de qualité ou non
- Format 8 bits, 24 bits ou 32 bits
-
...
-
Traitement particulier applicable aux images bitmaps: Réalisation d'opérations de traitement d'image visant à en changer les caractéristiques:
- Afficher en fausses couleurs
- Augmenter/diminuer la luminosité
- Augmenter/diminuer le contraste
- Flouter
- Extraire les contours
- Négativer
-
...
-
Traitement mathématique de chaque pixel de la matrice de pixels représentant l'image
-
Calcul de la nouvelle valeur d'un pixel à partir de son ancienne valeur
-> Filtrage spectral -
Calcul de la nouvelle valeur d'un pixel à partir de son ancienne valeur ainsi que des valeurs d'autres pixels (généralement les pixels voisins)
-> Filtrage matriciel
-
Calcul de la nouvelle valeur d'un pixel à partir de son ancienne valeur

Image originale

Image floutée
Remplacement de chaque pixel par la moyenne de ce pixel et des pixels voisins

Image après extraction de contours
Gradiant calculé sur les pixels voisins
|
/** |
| Exemple de traitement d'image |
-
Jeu de la vie
- Une grille de booléens initialisés à vrai ou à faux
-
Chaque cellule évolue en fonction du contenu de ses 8 voisines
- Si 2 voisins à vrai, la cellule ne change pas
- Si 3 voisins à vrai, la cellule passe à vrai
- Dans tous les autres cas, la cellule passe à faux
- Automate cellulaire
- Evolution d'un eco-système







Placement aléatoire -> Stabilisation au bout d'un certain nombre d'étapes
Exemple d'exécution
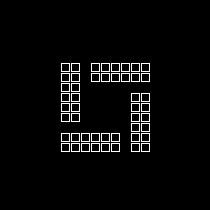
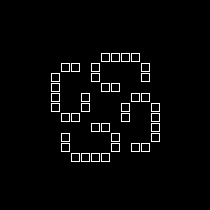
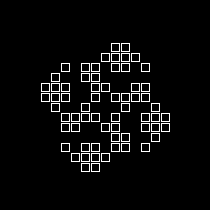
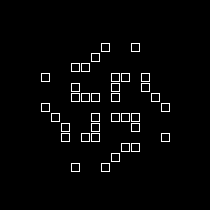
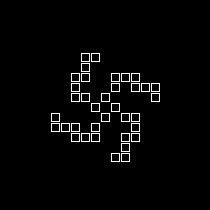
Evolution cyclique en place: Galaxie
Exemple d'exécution





Evolution cyclique avec déplacement régulier: Vaisseau
Exemple d'exécution
- Jeux 2D

Tétris

Candy Crush