Semestre 2 ST
Matrices de variables
| Cours | TD - Corrections | TP |
![]()
Exercice n°1
On considère une matrice d'entiers composée de 20 lignes de 8 colonnes. On souhaite effectuer diverses recherches au sein de ce tableau.
a) Développer un sous-algorithme permettant de calculer la plus petite valeur contenue dans un tel tableau.
b) Développer un sous-algorithme permettant de calculer la position de la plus petite valeur contenue dans un tel tableau.
c) Développer un sous-algorithme permettant de calculer l'indice de la ligne dont la somme des valeurs est la plus grande.
Exercice n°2
On manipule des matrices de réels.
a) Développer un sous-algorithme permettant de copier une matrice dans une matrice. Leurs tailles sont supposées identiques.
b) Développer un sous-algorithme permettant de copier la matrice transposée d'une matrice dans une matrice. Leurs tailles sont supposées compatibles. Transposer une matrice est l'opération consistant à permuter ses valeurs autour de la diagonale principale.
c) Développer un sous-algorithme permettant de réaliser la transposition d'une matrice. La transposition se fait "en place", sans utilisation d'une matrice auxiliaire.
Exercice n°3
On manipule des tableaux et des matrices de caractères.
a) Développer un sous-algorithme permettant de générer un tableau à partir d'une matrice. Le tableau généré sera de taille nl*nc où nl et nc sont les nombres de lignes et de colonnes de la matrice. Les valeurs de la matrice seront reportées les unes à la suite des autres dans le tableau ligne de la matrice après ligne de la matrice (de gauche à droite et de bas en haut).
b) Développer un sous-algorithme permettant de générer une matrice à partir d'un tableau. Outre le tableau, le sous-algorithme aura comme paramètre le nombre de lignes et le nombre de colonnes de la matrice à générer. Le report des valeurs dans la matrice est effectué séquentiellement de gauche à droite et de bas en haut. S'il n'y a pas assez de place, le report sera arrêté une fois la matrice pleine. S'il y a plus de place que nécessaire, les emplacements non remplis seront affectés avec le caractère espace.
Exercice supplémentaire n°1
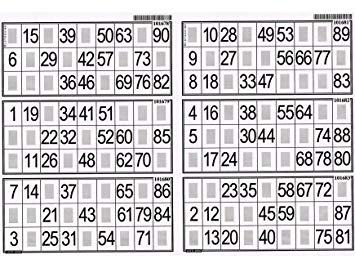
Vous êtes l'organisateur d'un Loto Quine. Dans ce jeu, les joueurs achètent des cartons comportant des nombres répartis sur une grille. Le maître du jeu tire ensuite au sort des nombres et les annonce à l’ensemble des joueurs. Le premier joueur ayant complété l’ensemble des nombres présents sur l’une des lignes de ses cartons et l'ayant annoncé en criant "quine" gagne le premier lot mis en jeu. Le premier joueur ayant complété l’ensemble des nombres présents sur l’un de ses cartons et l'ayant annoncé en criant "carte" gagne le deuxième lot mis en jeu.
Le but de l’exercice consiste à développer un sous-algorithme de génération d’un carton.
Les caractéristiques précises d’un carton sont (voir exemples ci-dessous):
- La grille qu'il contient est constituée de 3 lignes de 9 colonnes.
- 15 nombres entiers sont placés aléatoirement. Ils sont tirés au sort entre 1 et 90. Un nombre ne peut être placé qu'une seule fois.
- Les nombres compris entre 1 et 9 sont placés sur la première colonne. Les nombres compris entre 10 et 19 sont placés sur la 2ème colonne. Les nombres
compris entre 20 et 29 sont placés sur la 3ème colonne et ainsi de suite jusqu’à la 8ème colonne qui contient les nombres compris entre 70 et 79.
Enfin, la 9ème et dernière colonne contient les nombres compris entre 80 et 90.
- Exactement 5 nombres sont placés sur chaque ligne répartis aléatoirement sur les 9 positions possibles.
- Chaque colonne comporte au minimum 1 nombre et peut en contenir 1 ou 2 autres. S’il y a 1 ou 2 nombres sur une colonne, ceux-ci sont placés
aléatoirement sur les 3 positions possibles.
Exercice supplémentaire n°2
On considère une matrice de NxM "cellules". Chaque cellule possède 4 cellules voisines (à droite, à gauche, en haut et en bas). Un déplacement élémentaire entre cellules ne peut être réalisé qu'entre deux cellules voisines. La "distance" existant entre deux cellules est le nombre minimum de déplacements élémentaires permettant de passer de la première cellule à la seconde.
a) Développer un sous-algorithme permettant de calculer la matrice des distances existant entre chaque cellule d'une matrice NxM et une cellule de position arbitraire.

Calcul des distances pour une matrice de 14 lignes de 20 colonnes
et la position de départ (8,5)
On pourra calculer les distances en les attribuant en motif concentrique autour de la position de départ. Il est bien entendu que l'on ne devra pas "déborder" de la matrice.
On considère que la matrice de taille NxM est une matrice de booléens. Cette matrice représente un plateau de jeu définissant 2 territoires (vrai pour le joueur n°1, faux pour le joueur n°2).

Exemple de plateau de jeu
b) Développer un sous-algorithme permettant de calculer la matrice des distances existant entre chaque cellule d'une matrice NxM et une cellule de position arbitraire. Dans cette version, le passage par une cellule du territoire du joueur opposé au joueur auquel appartient la cellule de départ est interdit. Une distance égale à -1 signifie une cellule non atteignable.

Distances à partir de la position initiale (8,5)

Distances à partir de la position initiale (1,8)
Contrairement à la question (a), il n'est plus possible d'attribuer les distances de manière simple et déterministe. Une méthode pourra consister à programmer un traitement itératif consistant, à chaque itération numérotée i, à parcourir l'intégralité de la matrice à la recherche de chaque cellule à laquelle une distance n'a pas encore été attribuée et qui touche une cellule à laquelle une distance a été attribuée. Chacune de ces cellules se voit attribuer comme distance la valeur i. Ce processus itératif se poursuit tant qu'au moins une cellule se voit attribuer une distance au cours d'une itération de traitement.