Les mathématiques
de l'Infographie
DE TRAVAIL
RAPPELS
Vecteur
Matrice
Norme
Vecteur normal
Produit scalaire
Produit vectoriel
Produit matrice par vecteur
Produit matrice par matrice
REPRÉSENTATION
DES OBJETS ET TRANSFOR-
MATIONS GEOMETRIQUES
Coordonnées
homogènes
Translation
Rotation
Homothéties
Composition
de transformations
Espaces de travail et outils nécessaires
Espaces euclidiens (continus): R2, R3
- Utilisation d'équations de modélisation d'objets
- Utilisation de positions (coordonnées de sommets, points de contrôle, ...)
- Utilisation de directions (normales utilisées pour les éclairages, directions d'orientation, ...)
Les objets sont modélisés géométriquement dans un espace (repère) global avec utilisation de transformations géométriques portant sur ce repère.
Au cours du processus de visualisation, un changement de repère est effectué, permettant de transformer les coordonnées globales en coordonnées écran utilisées pour le rendu.
-> Utilisation d'outils mathématiques de modélisation des objets géométriques visant, entre autres buts, à déterminer leurs sommets et les
normales à ces sommets
-> Utilisation d'outils mathématiques permettant de réaliser des transformations géométriques
Objets graphiques
- Point ou sommet (dimension euclidienne 0)
- Segment (dimension euclidienne 1)
- Rectangle (dimension euclidienne 1)
- Ligne brisée et polygone (dimension euclidienne 1)
- Facette (dimension euclidienne 2)
- Patch (dimension euclidienne 2)
- Cube, sphère, cylindre, tore (dimension euclidienne 3)
- Surface quadrique (dimension euclidienne 2)
- Courbe cubique (dimension euclidienne 1)
- Surface bicubique (dimension euclidienne 2)
- …
La dimension euclidienne d'un objet indique s'il s'agit d'un sommet (0), d'une courbe (1), d'une surface (2) ou d'un volume (3). Il s'agit du nombre d'inconnues dans le mode de représentation par équation(s) paramétrique(s) (voir plus loin).
Représentation cartésienne d'un objet graphique
Représentation sous forme d’équations ne faisant pas intervenir d’autre paramètre variable que les coordonnées des points définissant l’objet.
Droite dans le plan (2D): ax + by + c = 0
Plan dans l’espace (3D): ax + by + cz + d = 0
Droite dans l’espace (3D) (intersection de deux plans):
Surface sphérique de centre (cx,cy,cz) de rayon r dans l'espace (3D):
(x-cx)2 + (y-cy)2 + (z-cz)2 = r2
Sphère (volume sphérique) de centre (cx,cy,cz) de rayon r dans l'espace (3D):
(x-cx)2 + (y-cy)2 + (z-cz)2 <= r2
Représentation paramétrique d'un objet graphique
Représentation sous forme d’un système d'équations déterminant chacun des points de l’objet par une équation
pour chacune des dimensions de l'espace.
Il y a donc autant d'équations que de dimensions dans l'espace de modélisation.
Ces équations sont fonctions de constantes et de un ou plusieurs paramètres variables indépendants. Le nombre de ces paramètres
est égal à la dimension euclidienne de l'objet.
Droite dans le plan (2D):
t appartient à R, 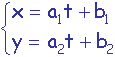
Droite dans l’espace (3D):
t appartient à R, 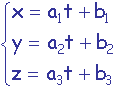
Plan dans l’espace (3D):
t et u appartiennent à R, 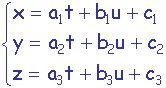
Surface sphérique de centre (cx,cy,cz) de rayon r dans l’espace (3D):
| t appartient à [-p/2,p/2] u appartient à [0,2p] |
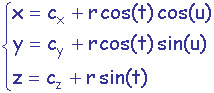
|
Sphère (volume sphérique) de centre (cx,cy,cz) de rayon Ra dans l’espace (3D):
| t appartient à [-p/2,p/2] u appartient à [0,2p] r appartient à [0,Ra] |
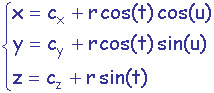
|
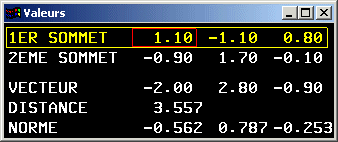
On appelle vecteur ![]() une suite ordonnée de n valeurs numériques extraites du même ensemble E (par exemple N, Z, R, C,…).
une suite ordonnée de n valeurs numériques extraites du même ensemble E (par exemple N, Z, R, C,…).
n est appelé la dimension du vecteur. Le vecteur est défini dans En. En est un espace de dimension n.
Exemple: ![]() dans Z2 ,
dans Z2 , ![]() dans R3.
dans R3.
On appelle matrice M un tableau à deux indices de n*m valeurs numériques extraites du même ensemble E.
Exemple:
 n = 4, m = 5.
n = 4, m = 5.
Usuellement n et m sont le nombre de lignes et le nombre de colonnes de la matrice.
Si n = m la matrice est dite carrée.
Soit le vecteur ![]() =
= ![]() de R2, norme(
de R2, norme(![]() ) =
) = ![]() =
= ![]()
Soit le vecteur ![]() =
= ![]() de R3, norme(
de R3, norme(![]() ) =
) = ![]() =
= ![]()
Une définition intuitive de la norme d'un vecteur est la longueur de ce vecteur.
Vecteur normé et vecteur normal
On appelle vecteur normé un vecteur de norme égale à 1.
![]() et
et ![]() sont les 2 vecteurs normés colinéaires au vecteur
sont les 2 vecteurs normés colinéaires au vecteur ![]() .
.
On appelle vecteurs normaux (ou plus simplement normales) à une surface plane définie dans R3 les deux vecteurs normés
![]() et
et ![]() de R3 orthogonaux à cette surface.
de R3 orthogonaux à cette surface.
Si la surface n’est pas plane, il existe un couple différent de normales en chaque point où l’équation de la surface
est dérivable selon les deux paramètres variables de sa définition paramétrique.
Quelle que soit la surface, ![]() = -
= -![]() en chaque point où ces vecteurs existent.
en chaque point où ces vecteurs existent.
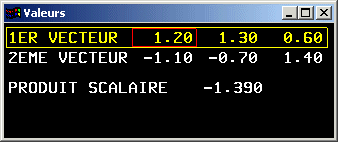
Produit scalaire entre deux vecteurs
Soient deux vecteurs ![]() =
= ![]() et
et ![]() =
= ![]() de R2,
de R2,
le produit scalaire ![]() .
.![]() = x1 x2 + y1 y2.
= x1 x2 + y1 y2.
Soient deux vecteurs ![]() =
= ![]() et
et ![]() =
= ![]() de R3,
de R3,
le produit scalaire ![]() .
.![]() = x1x2 + y1y2 + z1z2.
= x1x2 + y1y2 + z1z2.
Propriétés
Si q est l’angle entre ![]() et
et ![]() ,
, ![]() .
.![]() =
= ![]()
![]() cos(q).
cos(q).
Cette propriété explique que le produit scalaire de deux vecteurs est égal à 0 si ces deux vecteurs sont orthogonaux.
Si on inverse l’un des deux vecteurs, le résultat de leur produit scalaire est négativé.
Si les deux vecteurs sont normés, leur produit scalaire est égal au cosinus de l'angle qu'ils forment.
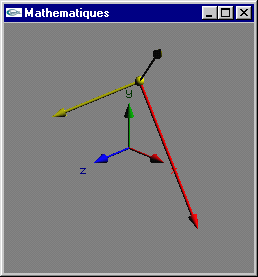
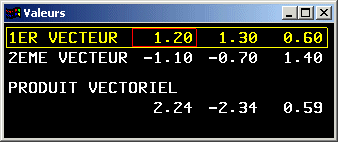
Produit vectoriel entre deux vecteurs
Soient deux vecteurs ![]() =
= ![]() et
et ![]() =
= ![]() de R3,
de R3,
le produit vectoriel ![]() ^
^![]() est le vecteur
est le vecteur 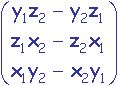 .
.
Propriétés
Si q est l’angle entre les vecteurs ![]() et
et ![]() ,
,
![]() =
= ![]()
![]() abs(sin(q)).
abs(sin(q)).
Si on inverse l’un des deux vecteurs, le vecteur résultat du produit vectoriel est inversé.
![]() ^
^![]() =
= ![]()
![]() ^
^![]() est orthogonal à
est orthogonal à ![]() et à
et à ![]() .
.
Soient un vecteur ![]() de dimension n (vi, 1 <= i <= n) et une matrice carrée M de dimension n x n (mij, 1 <= i <= n, 1 <= j
<= n).
de dimension n (vi, 1 <= i <= n) et une matrice carrée M de dimension n x n (mij, 1 <= i <= n, 1 <= j
<= n).
Le vecteur ![]() produit de M par
produit de M par ![]() est
est ![]() = M *
= M * ![]() .
.
wi =  , 1 <= i <= n
, 1 <= i <= n
On calcule le produit de chaque ligne de la matrice par le vecteur colonne.
Exemple:
 .
.  =
= 
Soient deux matrices M1 et M2 de dimensions respectives:
n x m (m1ij, 1 <= i <= n, 1 <= j <= m),
m x p (m2ij, 1 <= i <= m, 1 <= j <= p).
La matrice M produit de M1 par M2 est de dimension n x p et est calculée par la formule suivante:
mij = 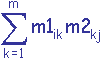 (1 <= i <= n, 1 <= j <= p)
(1 <= i <= n, 1 <= j <= p)
Exemple:
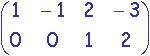 .
. 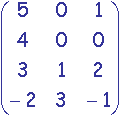 =
= 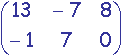
Si M1 et M2 sont deux matrices carrées de dimension n x n, le produit de M1 par M2 est une matrice carrée de dimension n x n.
Représentation des objets et transformations géométriques
L'objet de base "point" est représenté par un vecteur de n coordonnées (n est la dimension de l'espace de travail):
![]() en 2 dimensions ,
en 2 dimensions , ![]() en 3 dimensions.
en 3 dimensions.
Les coordonnées sont généralement soit toutes réelles (R) soit toutes entières (Z).
Un objet graphique pourra être modélisé par un ensemble de facettes elles-mêmes modélisées par un ensemble de sommets.
Les directions sont aussi réprésentées par des vecteurs à 2 dimensions dans un espace 2D et des vecteurs à 3 dimensions dans un espace 3D.
Cas particulier: Un objet paramétrique est défini implicitement par les équations le représentant.
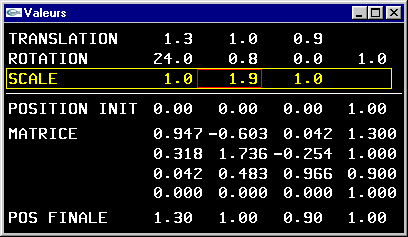
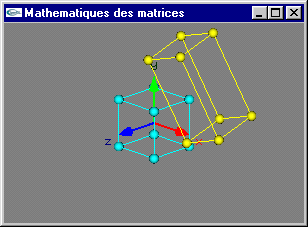
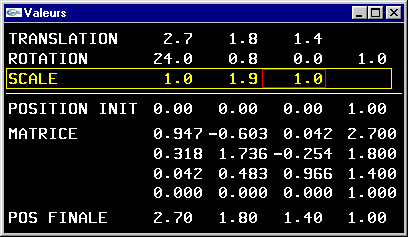
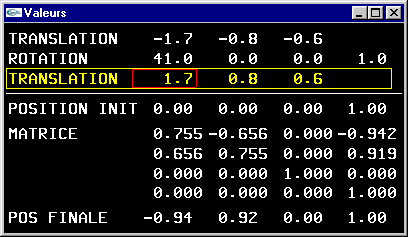
Une transformation géométrique de type rotation ou zoom appliquée aux positions prend la forme d'une matrice carrée M de dimension la dimension de l'espace de travail. Cette matrice appliquée à une position P donnera la position P' transformée par calcul du produit matriciel P' = M * P.
Important: Les directions sont aussi transformées par cette technique -> Outil unique pour ces 2 catégories d'objet.
Exemples de matrices de transformation: En trois dimensions
-
identité:
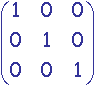
-
rotation d'angle qx autour de l'axe Ox:
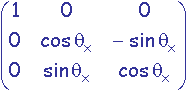
-
rotation d'angle qy autour de l'axe Oy:
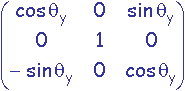
-
rotation d'angle qz autour de l'axe Oz:
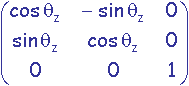
-
zoom uniforme de rapport r:

Problème: Les translations ne sont pas représentables au moyen de cette définition.
On utilise des vecteurs à n+1 coordonnées dans un espace de représentation de dimension n:
les n coordonnées classiques + une coordonnée supplémentaire.
Les transformations géométriques sont réalisées à partir de matrices carrées de dimension
(n+1) * (n+1).
Les translations sont modélisées à partir des valeurs contenues sur la n+1ième colonne de la matrice de transformation
tandis que les rotations et mises à l'échelle utilisent plus classiquement la sous-matrice n * n supérieure gauche.
La n+1ième ligne est la ligne correspondante de la matrice identité (uniquement des 0.0 sauf un 1.0 en dernier sur la diagonale).
La n+1ème coordonnée d'un vecteur est initialisée à 1.0 pour représenter une position, ou à 0.0 pour représenter une direction (invariante par translation).
Dans R2, la position ![]() =
= ![]() . Dans R3,
. Dans R3, ![]() =
= ![]() .
.
Dans R2, la direction ![]() =
= ![]() . Dans R3,
. Dans R3, ![]() =
= ![]() .
.
Manipulations géométriques
Soit une position ou une direction X connue sous la forme d'un vecteur ![]() .
.
Soit une transformation géométrique définie par la matrice A donnée en coordonnées homogènes.
Le vecteur ![]() transformé de
transformé de ![]() par la matrice A est
par la matrice A est ![]() = A.
= A.![]() .
.
|
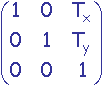
|
|
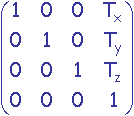
|
|
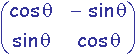
|
|
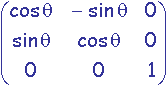
|
|
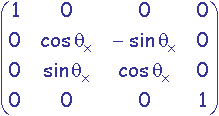
|
|
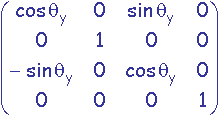
|
|
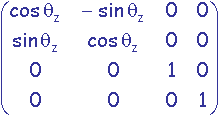
|
-
En coordonnées homogènes 3D, rotation d'angle q autour de l'axe
 normé passant par l'origine:
normé passant par l'origine:
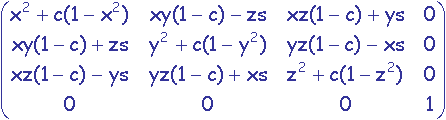
avec c = cos(q) et s = sin(q)
Zooms uniformes
-
En coordonnées homogènes 2D :

-
Dans coordonnées homogènes 3D :

Affinités orthogonales
|
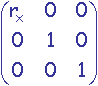
|
|
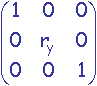
|
|
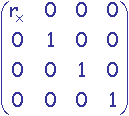
|
|
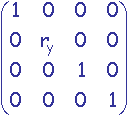
|
|
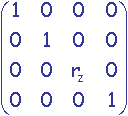
|
Composition de transformations
On désire réaliser une transformation A sur une position (resp. une direction) X puis ensuite la transformation B pour obtenir la position (resp. la direction) Y, on pourra réaliser:
Y = A.X puis Y = B.Y qui est équivalent à Y = B.(A.X) ou bien encore Y = (B.A).X.
Toutes les matrices de transformation (canoniques comme définies ci-avant ou totalement arbitraires) sont composables pour obtenir une transformation représentative de la réalisation successive de ces transformations géométriques.
Les matrices de transformation apparaissent dans le produit dans l'ordre inverse de l'ordre selon lequel elles interviennent effectivement.
Propriétés
Associativité des produits matrice par matrice et matrice par vecteur.
Attention!!! Non commutativité des produits matriciels.
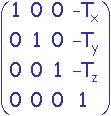
On désire établir la transformation consistant à effectuer une rotation de qz radians autour de l'axe colinéaire à z passant par le point P de coordonnées (Tx,Ty,Tz).
Cette transformation M est réalisée en amenant P à l'origine par une translation T de -P, puis en effectuant une rotation R d'angle qz autour de l'axe Oz, et enfin en ramenant P à sa position initiale par une translation T' de P.
M = T'.R.T
=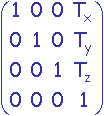 .
.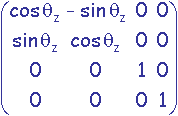 .
.
= .
.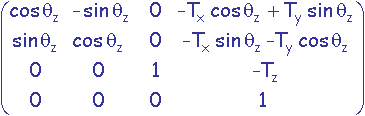
= 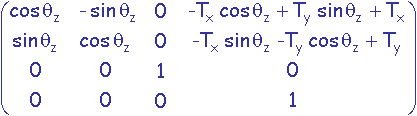
Formulation transposée
Si la convention de notation transposée est utilisée, les vecteurs coordonnées ne sont plus verticaux, mais horizontaux.
Le produit matriciel entre une position ou une direction et une matrice ne prend plus la forme: Y = A.X, mais Y = X.A.
Les matrices associées aux transformations sont différentes: Ce sont les matrices transposées.
Exemple
Matrice 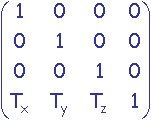 et non
et non 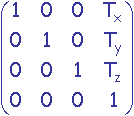
pour une translation de ![]() dans R3
dans R3
Les compositions de transformations seront réalisées en multipliant le vecteur initial par les matrices transformations dans l'ordre où elles interviennent et non plus dans l'ordre inverse.
"Quel codage mathématique des objets utiliser?" et "Quels outils mathématiques employer pour réaliser les manipulations nécessaires?" sont les deux premières questions que l'on doit se poser pour réaliser l'implantation des objets manipulés dans une application graphique.
On a souvent intérêt à structurer au maximum les données que l'on manipule.
L'utilisation des coordonnées homogènes est la technique de représentation la plus employée pour les positions et les déplacements. Une transformation géométrique sera généralement représentée par une matrice en coordonnées homogènes.
Les surcoûts en terme de calcul et d'occupation mémoire associés à la manipulation de coordonnées homogènes sont largement compensés par les facilités opérationnelles (ambiguïté des transformations géométriques, composition des transformations géométriques, ambiguïté position-direction, ...) qu'offrent ce mode de représentation.