La modélisation de scènes
en Infographie
PRINCIPES DE MODÉLISATION
Ensembles de facettes
Objets canoniques
Objets C.S.G.
Surfaces contrôlées
GÉOMÉTRIE
DES OBJETS
Inconvénients
et avantages
Plusieurs étapes pour la conception d'une application à affichage graphique trois dimensions :
- Détermination de la (des) scène(s) devant être représentée(s)
- Modélisation géométrique de cette(ces) scène(s)
- Conception et placement des objets
- Animation
- Placement des textures, des matériaux et des lumières
- Définition d'une caméra virtuelle
- Programmation
Principes de base pour la modélisation d'une scène 3D
Première action : Définition précise de l'espace et du repère dans lequel va être effectuée la modélisation de la scène
- Espace généralement euclidien entier ou réel à deux (x,y) ou trois (x,y,z) dimensions
- Repère généralement orthonormé et direct
- Espace et repère fréquemment qualifiés de "globaux" ou de "de modélisation"
Par analogie avec notre monde concret, définition des aspects suivants pour le repère :
- Position (son origine)
- Orientation (son plan de l'horizontale, sa direction de la verticale)
- Sens direct ou indirect
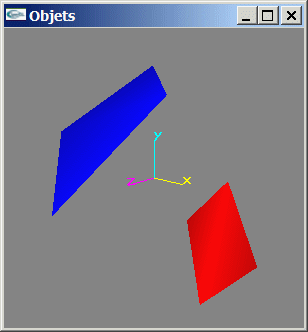
Deuxième action : Modélisation par assemblage d'"objets"
-> Union de ces objets
-> Création de la scène
![]()
Modélisation à base d'ensembles de facettes
Objet de base : la facette
- Surface plane délimitée par une boucle de sommets 3D
- Triangulaire ou non
- Généralement obligatoirement plane
- Fréquemment obligatoirement de bord convexe
Facettes utilisées en grand nombre pour modéliser des surfaces planes ou courbes (par approximation géométrique avec utilisation d'un très grand nombre de petites facettes)
-> Ensemble de facettes adjacentes (sommets et cotés communs)
Volumes modélisés par de telles surfaces se refermant sur elles-mêmes
-> Volumes creux! (pas gênant tant que l'on n'entre pas dedans)
Remarque
Objet le plus basique : le sommet (position dans l'espace)
Deux sommets pour définir un segment de droite
Au minimum trois sommets (liste ordonnée) pour définir une facette
-> Segments et facettes définis à partir de sommets
![]()
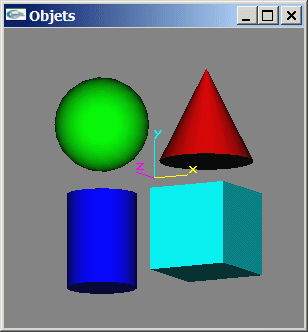
Modélisation à base d'objets canoniques
Deux types d'objets canoniques :
- l'ensemble de facettes, c'est à dire des objets connus uniquement par les facettes géométriques qui les composent
- le sommet, la courbe, la surface, le volume, ..., c'est à dire des objets entièrement caractérisés par un type géométrique élémentaire et par la donnée d'un jeu minimum de valeurs numériques
caractéristiques permettant via des équations mathématiques de déterminer toutes les caractéristiques géométriques nécessaires
Exemples : le cube, la sphère, le cylindre, le cône, le tore, le teapot, ...
Les objets géométriques canoniques, quels qu'ils soient, sont de caractéristiques précisément connues. Exemple: Le cube est centré sur l'origine, a ses faces orthogonales aux axes et a pour côté la longueur 1.
Précision : Suivant l'algorithme de rendu utilisé au moment de la phase de dessin, les objets géométriques qui ne sont pas des ensembles de facettes auront peut-être à être transformés en ensembles de facettes les approximant plus ou moins bien. Le développeur aura alors à sa disposition des primitives d'affichage graphique qui pourront être paramétrées pour permettre d'obtenir une plus ou moins grande précision de transformation, c'est à dire obtenir plus ou moins de facettes.
Objets C.S.G. (Constructive Solid Geometry)
Deux opérations de composition en plus de l'union :
- Intersection
- Différence
-> Modélisation plus puissante
Technique issue de la CAO/CFAO
Technique utilisée en infographie au sein des logiciels de modélisation (modelers)
Technique généralement pas implantée dans les bibliothéques 3D "classiques", en particulier OpenGL et Direct3D
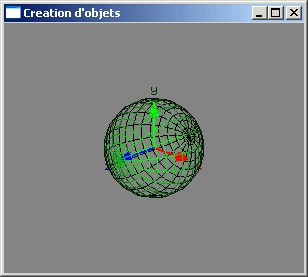
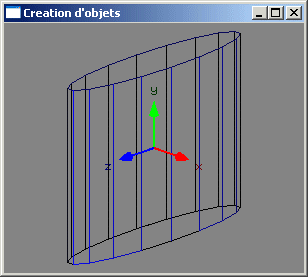
Géométrie des objets canoniques
Utilisation de transformations géométriques permettant de "changer" (transformer) les objets
"Mauvaise" façon de voir : Modélisation d'un objet quelconque à partir de son objet canonique auquel sont appliquées des transformations géométriques successives ayant pour but de le placer, de l'orienter et d'en définir les dimensions.
Meilleure façon de voir : Le repère de modélisation (celui "dans" lequel tout objet de la scène est modélisé au moment de sa génération) est
transformable par applications successives (par compositions) de transformations géométriques.
L'objet canonique n'est créé qu'après réalisation de ces transformations géométriques.
La création d'un objet est donc toujours canonique dans le repère de modélisation en cours au moment de la création.
-> Vu dans le repère initial, l'objet n'est pas canonique.
-> Si le repère en cours est correctement configuré, l'objet sera créé avec les caractéristiques souhaitées (en particulier une position, une orientation et
des dimensions) dans le repère de modélisation.
![]()
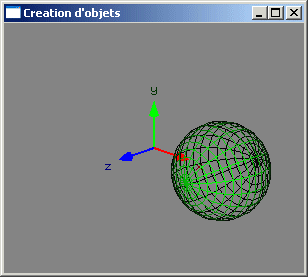
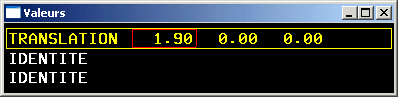
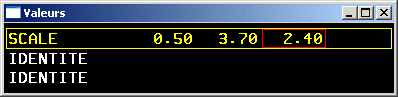
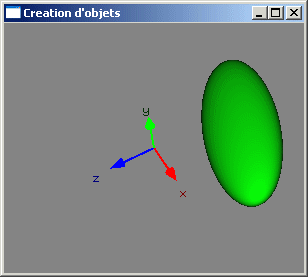
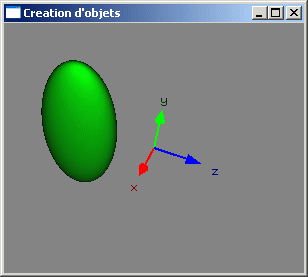
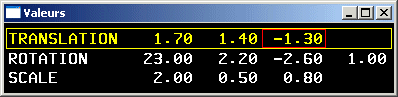
Transformations géométriques 3D
- translation (de vecteur (dx, dy, dz))
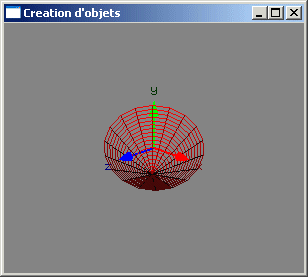
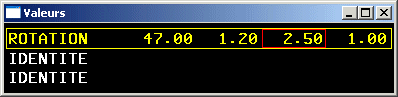
- rotation (d'angle a autour de l'axe de direction (dx, dy, dz) passant par l'origine)
- homothéties (zooms, mises à l'échelle, affinités orthogonales) (d'axe un des axes (x, y ou z) du repère, de rapport (rx, ry ou rz) selon cet axe et par rapport au plan constitué des deux autres axes)
Créer un objet placé, orienté et dimensionné reviendra fréquemment à réaliser dans l'ordre une translation, une rotation et un zoom sur le repère de modélisation puis à créer l'objet canonique au sein du repère tel qu'obtenu après ces transformations.
Inconvénients et avantages de cette technique de modélisation
Inconvénients :
- Complexe ?
Comment faire plus simple ? - Inefficace ?
Comment faire plus efficace ? - Technique limitée à quelques types d'objets canoniques ?
Non car on peut créer des objets canoniques modélisés par facettes même si c'est probablement plus simple de les modéliser par leurs équations mathématiques
Avantages :
- Bonne connaissance de chaque objet (connu par son type canonique et les transformations géométriques appliquées)
- Facilitation de certaines opérations mathématiques (exemple : calcul de la normale à une facette d'un cube ou à un point d'une sphère)
- Possibilité de lier intrinsèquement au cours de la phase de modélisation les objets d'une scène qui le sont effectivement dans la "scène réelle"
-> Modélisation hiérarchique - Si l'algorithme de rendu le permet, pas de facettisation lors du dessin.
Modélisation à base de surfaces contrôlées
Surface contrôlée : Objet défini par la donnée d'équations mathématiques spécifiques à son type de surface contrôlée et par la définition de sommets (points de contrôle) visant à contrôler sa forme
Tout objet de ce type nécessite le paramètrage de sa forme par placement
de ses points de contrôle.
Tout objet de ce type supportera les transformations géométriques de modélisation par transformation géométrique de ses sommets de contrôle.
-> Objet canonique comme les autres
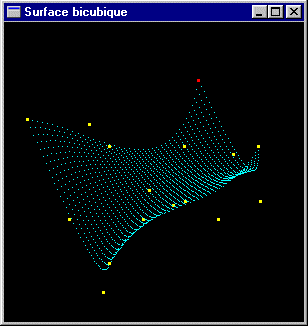
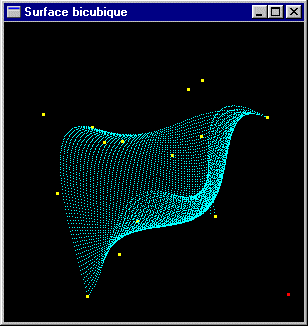
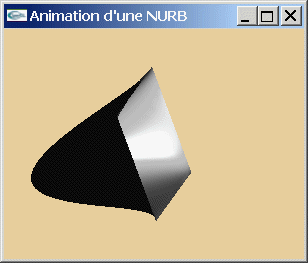
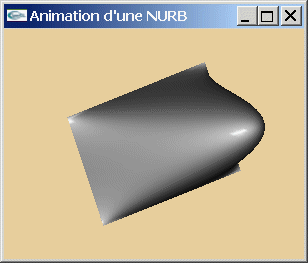
Exemple : les surfaces paramétriques bicubiques, les NURBS
| Surfaces bicubiques |
|
|
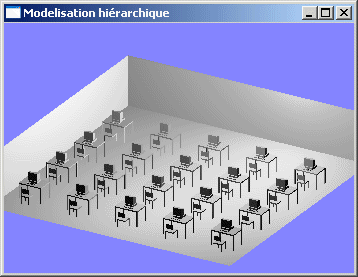
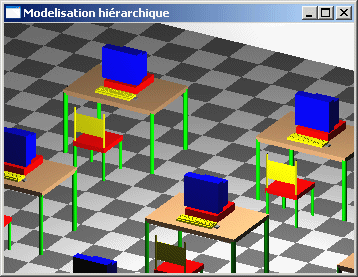
Il est recommandé d'effectuer le travail de modélisation par assemblage hiérarchisé.
Exemple : Une salle de TP sera modélisée par des tables, des chaises et des ordinateurs. Une chaise sera modélisée par quatre pieds, une assise et un dossier. Une table sera modélisée par un plateau et quatre pieds. Un ordinateur sera modélisé par un clavier, une souris, une UC et un écran...
Cette technique permet de réutiliser les objets si la primitive conçue pour chacun d'eux est correctement renseignée :
- Repère de modélisation associé
- Taille de l'objet dans ce repère
- ...
Cette technique permet aussi de faciliter le développement des objets car elle apporte beaucoup de souplesse :
- "Substituabilité"
- Evolutivité
- Réutilisabilité
- ...
Outils logiciels de modélisation
Les outils logiciels mis à disposition par les librairies graphiques 3D pour modéliser des scènes incluent très souvent les fonctionnalités suivantes :
- Gestion d'une transformation géométrique courante (initialisée à l'identité)
- Création d'une (ou plusieurs) facette(s) quelconque(s) affectée(s) de la transformation géométrique courante
- Création d'un cube canonique affecté de la transformation géométrique courante
- Création d'une sphère canonique affectée de la transformation géométrique courante
- Création d'un cylindre canonique affecté de la transformation géométrique courante
- Création d'un cône canonique affecté de la transformation géométrique courante
- Composition de la transformation géométrique courante avec une translation
- Composition de la transformation géométrique courante avec une rotation
- Composition de la transformation géométrique courante avec une affinité orthogonale
- ...
Outre ces primitives, on rencontre fréquemment les primitives :
- Mémorisation temporaire (via une gestion de pile et des opérateurs push et pop) des caractéristiques de la transformation géométrique courante
- Réinitialisation à l'identité de la transformation géométrique courante
L'existence des opérateurs push et pop appliqués à la transformation géométrique courante fait qu'une scène peut être vue comme modélisée sous la forme d'une arborescence parcourue prioritairement en profondeur :
- Les nœuds terminaux sont les objets géométriques.
- Les nœuds internes sont les transformations géométriques.
- Les nœuds d'arité supérieure à 1 ayant comme fils au moins un nœud interne sont les nœuds où le repère courant aura été empilé pour pouvoir être dépilé après parcours complet de la branche fille pour ainsi assurer la restoration du repère au moment du retour sur le nœud.