L'illumination globale :
la radiosité
FACTEUR
DE FORME
Hémisphère
Hémicube
0. Introduction
Les algorithmes de rendu par Z-Buffer+Lambert+Gouraud ou Z-Buffer+Phong+Lambert ou encore par ray-tracing sont assez approximatifs en terme d'évaluation
des déplacements d'énergie à l'intérieur des scènes. Or, ce sont ces déplacements d'énergie qui ont pour conséquence l'éclairage
et donc la coloration des objets.
L'un des problèmes non résolu est lié à la localité des éclairages : Un objet n'est éclairé que s'il n'est pas situé au delà d'un
certain (petit) nombre de réflexions spéculaires et de réfractions successives, d'une diffusion générée sur un objet par une source lumineuse
définie "en tant que telle" dans la scène. La réalité est différente et plus complexe :
(1) Le nombre de réflexions (diffuses et spéculaires sur les objets) et de transmissions (à travers les objets) successives est virtuellement
illimité. Dans la réalité une limite existe liée à la vitesse à laquelle se propage la lumière (300000 km/s), mais, à cette vitesse, cette limite
est très grande.
(2) Tout objet A d'une scène éclaire directement un objet B de cette scène à partir du moment où B est directement visible depuis A. Des
phénomènes de réflexions diffuse, de réflexion spéculaire et de transmission sont donc potentiellement générés sur B par de la lumière reçue de A
et ont potentiellement été générés sur A par l'ensemble des objets qui l'éclairent.
L'algorithme de rendu par calcul d'illumination globale appelé aussi algorithme de rendu par radiosité a été conçu pour implanter une partie
de ces principes. Il vise ainsi à rendre les éclairages plus conformes à la réalité et, dans ce cadre d'action, à calculer ce que l'on appelle
habituellement l'éclairage ambiant.
Ses limitations fonctionnelles sont qu'il se base pour cela uniquement sur la modélisation des diffusions et ne rend en aucune manière les réflexions
spéculaires et les transmissions. Il ne permet donc pas, par exemple, de voir l'image d'un objet sur un autre objet réfléchissant comme le
permet de lancer de rayons, de voir les reflets des sources lumineuses sur les objets réflechissants comme le permet le Z-Buffer ou bien encore de
voir ce qui se trouve derrière les objets transparents comme le permettent le Z-Buffer et surtout le lancer de rayons. Il est d'ores et déjà
possible d'annoncer qu'il ne saurait être utilisé seul si le photo-réalisme est nécessaire.
Tous les objets d'une scène sont de même nature, qu'il s'agisse de lumières ou bien d'objets graphiques classiques. Ils émettent
tous de l'énergie sous la forme de radiations électromagnétiques. Ce phénomène les rend visibles car une partie de ce qu'ils émettent est
captée directement par l'oeil de l'observateur (ou par la caméra de visualisation), mais également lumineux et donc à même d'éclairer
les autres objets. Ce spectre d'émission (la radiosité) est la somme de deux composantes (chacune pouvant éventuellement être nulle) :
- une énergie émise intrinsèquement,
- une énergie émise par réémission diffuse d'une partie de l'énergie reçue en provenance des autres objets présents dans la scène.
Après une infinité (un très grand nombre) de réémissions successives des objets les uns sur les autres, un équilibre énergétique s’établit à l’intérieur
de la scène. Chaque objet est alors affecté d’une composante lumineuse. C'est cette lumière que nous voyons.
Les objets qui émettent intrinsèquement de l'énergie sont assimilables à des lumières au sens classique du terme même si, dans la pratique, tous
les objets sont des lumières à partir du moment où ils émettent intrinsèquement de la lumière et/ou ils réémettent une partie de la lumière qu'ils
reçoivent. Les objets qui n'émettent pas intrinséquement de lumière sont assimilables oux objets classiques.
2. Mise en application algorithmique
Le calcul de radiosité est effectué en plusieurs étapes :
(1) La scène est discrétisée en un ensemble de n surfaces élémentaires.
(2) Pour chaque couple de surfaces, la fraction d’énergie qui, émise par la première, est réceptionnée par la seconde est calculée. Cette
fraction d'énergie est appelée "facteur de forme".
(3) Un système de n équations linéaires à n inconnues est constitué à partir des facteurs de forme. Les n inconnues de ce système sont les
radiosités émises par chaque facette.
(4) Le système d’équations linéaires est résolu pour déterminer la radiosité de chacune des n surfaces. Cette valeur de radiosité nous
donne la quantité d'énergie émise par la surface qui est équivalent au niveau de gris de la surface si on devait parler en terme de "couleur".
(5) L'affichage final est réalisé en utilisant un algorithme classique d’élimination des parties cachées (Z-Buffer ou lancer de rayons)
auquel sont fournies les surfaces élémentaires et leurs niveaux de gris.
2.1. Décomposition de la scènes en surfaces élémentaires
Cette décomposition est obligatoire car les radiosités obtenues à l'étape 4 sont constantes sur chaque surface. Ainsi, si les objets étaient
gardés en tant que tels, ils seraient de couleur uniforme. Cela est bien entendu impossible car non conforme à la réalité de notre monde. C'est
en particulier le cas pour les objets courbes sur lesquels l'illumination est généralement variable (une sphère éclairée par une lumière ne l'est
que d'un coté) ou bien encore pour les grands objets qui même s'ils sont plans ne sont pas éclairés de la même façon sur l'ensemble de
leur surface si la lumière qui les éclaire est proche d'eux.
Ce type de décomposition ne nous est pas étranger car on le pratique déjà lorsque l'algorithme du Z-Buffer est utilisé. Les surfaces élémentaires
créées pour le calcul de radiosité seront du même type que pour le Z-Buffer : des surfaces planes triangulaires ou à la rigueur quadrangulaires.
Ce type de surface est en effet bien adapté au calcul des facteurs de forme réalisé à l'étape 2. Là où une grande précision d'éclairage est
souhaitée, il sera nécessaire de facettiser de façon plus poussée. Ce sera le cas par exemple près des sources lumineuses ou vers le bord des ombres
c'est à dire d'une manière générale dans les zones où l'illumination varie rapidement.
Remarque : Détecter les zones où l'illumination varie beaucoup nécessite de calculer l'illumination, ce qui est le but du calcul de radiosité.
On est donc en présence d'une situation assimilable à une situation de "deadlock" (interblocage) où on a besoin de connaître A pour
déterminer B qui nécessite lui-même de connaître A. La solution à ce problème ne peut donc être qu'adaptative et donc dynamique.
Un point fondamental est que la dichotomie entre les objets graphiques et les lumières n'est pas aussi claire en radiosité qu'elle l'est en Z-Buffer et en lancer de rayon. Tous les objets sont des sources lumineuses. Certain des objets émettent intrinséquement de la lumière et peuvent être assimilés à des lumières classiques, les autres objets ne sont que réémetteurs d'une partie de la lumière qu'ils reçoivent est sont assimilables aux objets graphiques classiques même s'ils concourent un peu à l'éclairage dans la scène. Quelles que soient leurs caractéristiques de radiosité (la lumière totale qu'ils émettent), les objets sont tous des volumes et sont tous facettisés. Les objets "lumières" peuvent être rapprochés des lumières ponctuelles (ou des spots si on gère un éclairage non isotrope) car ils sont placés en une position définie. En revanche ils ne se réduisent pas un point infiniment fin mais sont véritablement des objets muni d'une taille non nulle (éventuellement petite). Il n'existe pas d'équivalent aux lumières directionnelles car il faudrait pour cela être capable de placer virtuellement à l'infini un objet de taille probablement infinie, ce qui est difficilement faisable.
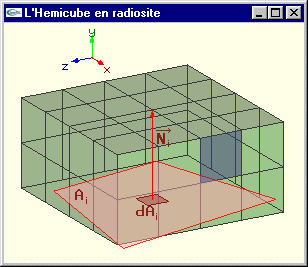
2.2. Calcul du facteur de forme entre deux surfaces
Définition : Le facteur de forme Fij est la fraction d’énergie qui quittant la surface Ai est reçue par la surface Aj.
Pour le calcul de Fij, les forme et orientation respectives des deux surfaces ainsi que de la présence éventuelle d’obstacles entre
elles sont prises en compte.
Par la suite, les surfaces seront considérées êtres des facettes.
|
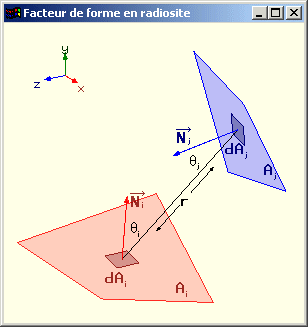
Facteur de forme d'une surface vis à vis d'une surface |
|
|
|
Touches de curseur et/ou souris pour manipuler le schéma |
Le facteur de forme dFdidj d’une surface différentielle dAi vers une surface différentielle dAj est :
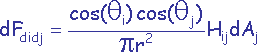
où θi est l’angle entre la normale à la surface Ai au point considéré et l’axe dAidAj, r est la
longueur de cet axe et H est la valeur de la visibilité (0 ou 1) de dAj depuis dAi.
Cette définition différentielle doit être intégrée sur les deux surfaces Ai et Aj pour trouver la valeur recherchée. C’est à dire :
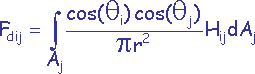
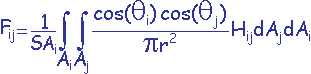 où SAi est l'aire de la surface
Ai
où SAi est l'aire de la surface
Ai
Problème : Comment réaliser cette intégration (qui est en fait une intégrale quadruple surface-surface) ?
Il n'existe pas de méthode analytique générale pour opérer cette intégration.
-> On emploie des solutions approximées.
Première approximation : On considère que Fij = Fdi j. Cette approximation n'est pas trop grossière si les facettes sont relativement petites les unes vues des autres.
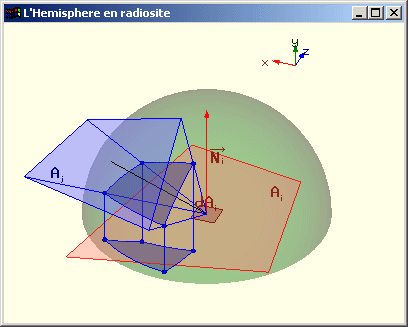
Calcul de Fdi j par projection sur l’hémisphère
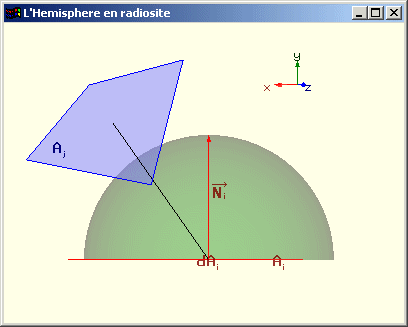
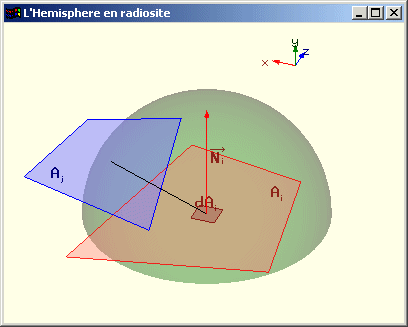
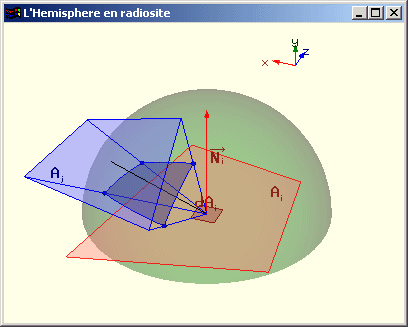
Une estimation de Fdi j est effectuée en projetant toutes les portions de Aj visibles depuis dAi sur l'hémisphère de rayon unitaire centrée sur dAi et dont la base est parallèle à dAi. On projette ensuite la portion de l'hémisphère ainsi définie sur le cercle base de l’hémisphère selon l’axe donné par la normale à Ai. On divise l’aire de la surface obtenue par l’aire du cercle base. Cette valeur nous donne une estimation de Fdi j et donc une estimation de Fij. Pour les calculs effectifs, dAi est généralement placé au centre de la facette Ai.
|
Méthode de l'hémisphère pour le calcul des facteurs de forme |
|
|
|
Touches de curseur et/ou souris pour manipuler le schéma |
Cette méthode a pour inconvénient de requérir l’emploi d'un opérateur de projection sur une sphère. Cette opération est couteuse en temps de calcul et surtout elle se marie mal avec la résolution nécessaire du problème de la détermination des portions visibles. Il est en effet obligatoire de tenir compte du fait que, vue depuis dAi, une facette peut être partiellement ou totalement masquée par une autre facette.
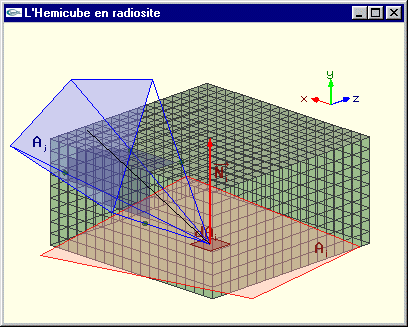
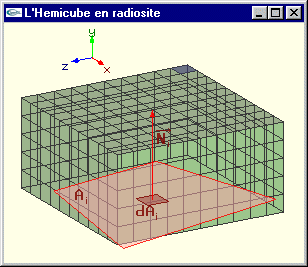
Calcul de Fdi j par projection sur l’hémicube
L'hémisphère de rayon 1.0 centrée sur dAi est remplacée par un hémicube de coté 2.0 centré sur dAi.
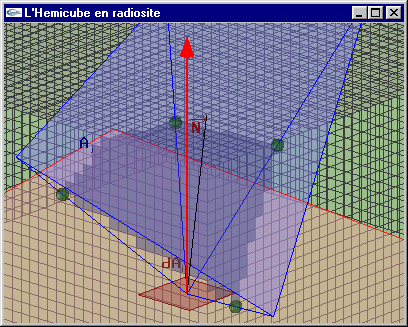
Chacune des cinq faces de cet hémicube est discrétisée en un certain nombre de cellules carrées identiques. La facette Aj est projetée
sur l'hémicube. Les cellules de l'hémicube qui font partie de la surface projetée sont déterminées.
|
Méthode de l'hémicube pour le calcul des facteurs de forme |
|
|
|
+/- pour augmenter/diminuer la discrétisation de l'hémicube a, A, b, B, c et C pour déplacer la facette j Espace pour changer de facette j Touches de curseur et/ou souris pour manipuler le schéma |
A chaque cellule p est associé un facteur de forme élémentaire approximé
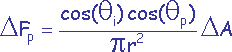
où θp est l’angle entre la normale à la cellule p et le vecteur entre dAi et p, r est la distance entre dAi
et p, et ΔA est la surface des cellules de l'hémicube.
On établit que pour une cellule p de centre de coordonnées (xp,yp,zp) située sur l’hémicube :
-
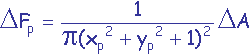 si p est une cellule située sur la face supérieure de l’hémicube.
si p est une cellule située sur la face supérieure de l’hémicube.
-
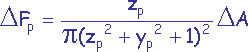 si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe x.
si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe x.
-
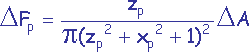 si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe y.
si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe y.
Remarque : Les valeurs ΔFp peuvent être pré-calculées si la résolution utilisée pour l'hémicube est toujours la même.
|
Méthode de l'hémicube pour le calcul des facteurs de forme Valeurs des facteurs de forme élémentaires des cellules de l'hémicube |
|
|
|
+/- pour augmenter/diminuer la discrétisation de l'hémicube a, A, b et B pour déplacer la cellule testée Espace pour changer de face sur l'hémicube Touches de curseur et/ou souris pour manipuler le schéma |
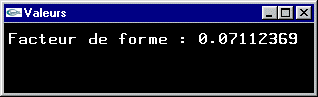
La somme des facteurs de forme élémentaires donne le facteur de forme recherché.
On pourra vérifier expérimentalement que la somme des facteurs de forme de l'ensemble des cellules élémentaires de l'hémicube est très voisine
de 1.0 quand la discrétisation de l'hémicube est importante, traduisant ainsi le fait que l'intégralité de l'énergie émise par dAi
est réceptionnée par les cellules de l'hémicube.
|
Méthode de l'hémicube pour le calcul des facteurs de forme Somme des facteurs de forme élémentaires pour obtenir le facteur de forme global |
|
|
|
+/- pour augmenter/diminuer la discrétisation de l'hémicube a, A, b, B, c et C pour déplacer la facette j Espace pour changer de facette j Touches de curseur et/ou souris pour manipuler le schéma |
Plus la discrétisation de l’hémicube est poussée, meilleure est l’estimation des facteurs de forme, mais plus long est le calcul.
La technique de l'hémicube permet de calculer une bonne approximation des facteurs de forme entre facettes.
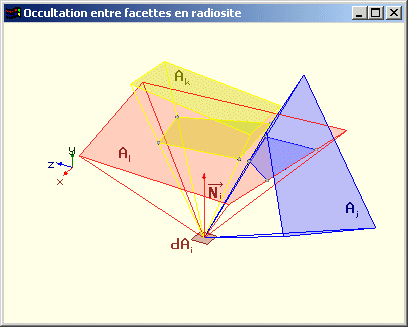
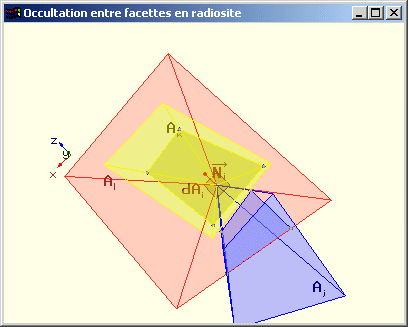
Problème : Elle ne permet pas de tenir compte des occultations éventuelles entre les facettes.
|
Occultations entre facettes pour le calcul des facteurs de forme |
|
|
|
Touches de curseur et/ou souris pour manipuler le schéma |
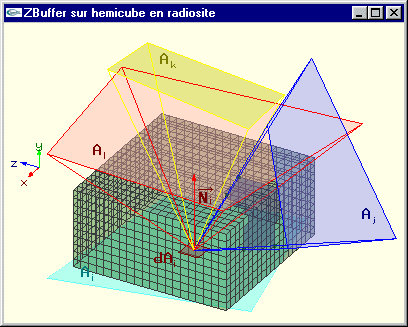
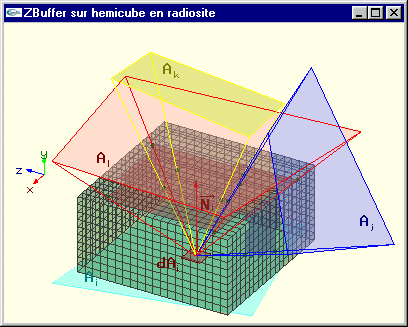
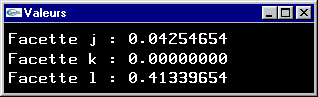
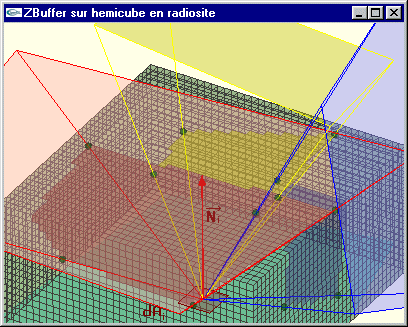
Plutôt que de calculer les facteurs de forme un par un, on effectue un traitement qui s'apparente très fortement à une élimination des parties cachées par Z-Buffer. Ainsi on va déterminer en une seule opération les facteurs de formes Fdi j pour toutes les facettes Aj vis à vis de dAi en réalisant une élimination des parties cachées depuis dAi pour l'ensemble des Aj de la scène projetés sur l'hémicube. Les faces de l'hémicube prennent donc le rôle d'écrans (5 écrans au total car 5 faces) et les cellules élémentaires le rôle des pixels de ces écrans.
|
Calcul d'une ligne de facteurs de forme en tenant compte des occultations |
|
|
|
Enter pour switcher entre une des trois facettes et les trois facettes ensemble pour le calcul des facteurs de forme a, A, b, B, c et C pour déplacer une facette Espace pour changer la facette déplaçable +/- pour augmenter/diminuer la discrétisation de l'hémicube Touches de curseur et/ou souris pour manipuler le schéma |
Remarque : On peut penser que la technique de calcul des facteurs de forme par hémicube a été imaginée parce qu'elle permet de s'appuyer sur l'implantation hard du Z-Buffer communément réalisée sur les adaptateurs graphiques. Une exploitation astucieuse de dispositifs matériels disponibles, puissants et peu onéreux est ainsi obtenue.
2.3. Constitution du système d’équations linéaires
Les facteurs de forme sont calculés. Il reste maintenant à les utiliser.
Soit une surface Ai. L'idée que la radiosité Bi émise par Ai soit égale à l'énergie émise intrinsèquement
par Ai à laquelle est ajoutée une partie de ce qu'elle reçoit de l'ensemble des surfaces de la scène, et qu'elle renvoie,
peut être traduite par la formule suivante :
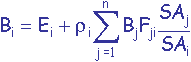 (1)
(1)
où Bj est la radiosité de la surface Aj (mesurées en énergie/unité de temps/unité de surface), Ei est l’énergie intrinsèque émise par la surface Ai, ρi est la réflectivité de la surface Ai, Fji est le facteur de forme de la surface j vers la surface i et SAi et SAj sont les aires des surfaces Ai et Aj.
La notion de réflectivité est introduite dans la formule (1). Il s'agit du coefficient numérique qui multiplié par l'énergie reçue par une
facette donne la quantité d'énergie réémise par cette facette. Les ρi sont donc compris entre 0.0 et 1.0. On peut dire qu'ils
s'apparentent aux coefficients de diffusion.
Les Ei sont les énergies émises intrinséquement par les surfaces. Celles qui jouent le rôle de lumière auront un Ei qui pourra
prendre n'importe quelle valeur strictement supérieure à 0.0 (y compris de très grandes valeurs). Celles qui jouent le rôle d'objet classique
auront un Ei égal à 0.0.
On établit que SAi Fij = SAj Fji, ce qui permet de reformuler (1) en :
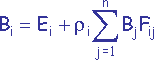 (2)
(2)
On rappelle que, dans la formule (2), les Bi et les Bj sont les inconnues à déterminer et que les termes, Ei, ρi et Fij sont sont des quantités connues. De façon à mieux exprimer les inconnues, la formule (2) peut être remaniée pour être présentée sous forme matricielle :
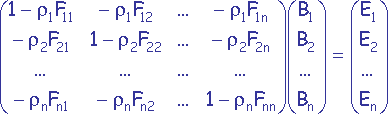 (3)
(3)
qui est en fait un système de n équations linéaires à n inconnues où les inconnues sont les radiosités Bi.
Remarque : La diagonale de la matrice n’est pas forcément égale à 1.0 (le facteur de forme d'une surface vis à vis d'elle-même peut être différent de 0.0) car une surface s non plane peut s’éclairer elle-même.
2.5. Résolution du système d’équations linéaires
Le système d'équations est généralement résolu en utilisant une méthode itérative : Jacobi ou Gauss-Seidel. Le but n'est pas de décrire précisément
ici ces méthodes de résolution qui revèlent du domaine des mathématiques et sortent donc du champ de l'informatique graphique. Seules quelques
idées maîtresses sont données.
Ces méthodes de résolution sont basées sur la génération d'une suite de solutions approximées qui converge inéluctablement vers la bonne solution.
On arrête la résolution du système quand un critère défini par l'utilisateur est vérifié. Dans le cadre particulier du calcul de radiosité, divers
critères peuvent être définis :
- différence inférieure à une valeur epsilon (méthode des moindre carrés par exemple) entre deux états successifs du vecteur des Bi,
- invariabilité des images obtenues en utilisant les Bi pour générer des images de la scène,
- ...
Une comparaison des méthodes de Jacobi et de Gauss-Seidel ne permet pas de conclure de façon universelle à l'avantage de l'une sur l'autre.
Gauss-Seidel présente habituellement une meilleure vitesse de convergence que Jacobi. En revanche Jacobi est aisément et efficacement parallélisable
alors que Gauss-Seidel l'est moins.
2.6. Affichage final
La résolution du système d'équations est réalisée. Le vecteur des radiosités (Bi ci-dessus) est connu. Celles-ci nous donnent les
illuminations des surfaces élémentaires que l'on peut traduire directement en tant que niveaux de gris.
S'il permet le calcul de ces niveaux de gris, le calcul d'illumination globale n'est absolument pas un algorithme de rendu au sens où
il produirait in fine une image. Il est donc nécessaire d'utiliser un algorithme qui permettra de générer cette image. Cela signifie à minima
la rasteristation des surfaces de la scène et l'élimination des parties cachées. Deux techniques sont à notre disposition : le Z-Buffer et le
lancer de rayons. Il est bien entendu que les calculs d'illumination par diffusion étant réalisés, cette phase finale de génération d'image
ne comporte pas ces calculs dans ces deux algorithmes.
Z-Buffer
Les surfaces élémentaires définies pour le calcul de radiosité sont assez naturellement directement recyclées pour le Z-Buffer. Ne plus faire de calculs d'illumination se traduit par le fait que Lambert et Phong ne sont plus utilisés. En revanche, on pourra continuer à utiliser Gouraud pour masquer les surfaces élémentaires.
Lancer de rayons
Il est possible d'utiliser les surfaces élémentaires définies pour le calcul de radiosité en tant qu'objets de la scène affichée en lancer de rayons. Cela conduit toutefois probablement à une scène composée d'un très grand nombre d'objet. Ce qui aura pour conséquence l'utilisation quasi-obligatoire d'un algorithme optimisé pour continuer à fonctionner dans cette situation. Il est aussi possible de "reconstituer" chaque objet initial de la scène en le munissant de son ensemble de valeurs d'illumination, et d'adpater la fonction de l'algorithme de lancer de rayons qui a pour but de réaliser les calculs de diffusion sur les objets pour qu'elle extrait les illuminations qu'elle calcule non plus d'une formule de type Lambert, mais de l'ensemble des illuminations de ces objets. En tout état de cause, les diffusions étant calculées au cours de la phase de radiosité, tous les "vrais" calculs de diffusion disparaissent. Signalons que, dans le lancer de rayons, les calculs de diffusion avaient pour conséquence la génération des ombres portées (test entre les rayons d'ombre et les objets de la scène) et que supprimer ces calculs ne supprimera pas les ombres portées car le calcul de radiosité intègre leur obtention (gestion des occultations entre surfaces lors du calcul des facteurs de forme). Les transmissions et réflexions spéculaires sont gardées dans le lancer de rayons pour obtenir des images plus réalistes. Il est toutefois à noter que ces phénomènes ne sont pas modélisés en radiosité et que donc, si dans la réalité tous les phénomènes de réflexion et transmissions concourrent à l'illumination de la scène, ce ne sera pas ici le cas.
2.7. Et les couleurs ?
La gestion des couleurs n'a pas été abordées dans les paragraphes précédents. Tel qu'il est décrit le calcul d'illumination global permet d'obtenir des images en niveau de gris mais pas en couleur. Pour passer en couleur, il ne suffit pas de considérer que chaque surface élémentaire est munie d'une teinte élémentaire car cela reviendrait à ignorer le fait que les surfaces éclairent les surfaces et que donc les déplacements d'énergie dans la scène sont "colorés". L'obtention d'images en couleur reste toutefois relativement simple : le calcul est réalisé trois fois, une fois pour le rouge, une fois pour le vert et une fois pour le bleu de façon à obtenir des radiosités selon ces trois composantes de base qui seront utilisées comme couleurs pour les surfaces de la scène lors de l'affichage final. Ce sont donc trois sytèmes d'équation linéaires qui sont résolus. Il est bien évident que ces systèmes sont différents et que l'on ne calcule pas trois fois la même chose. Dans la présentation matricielle (3) les inconnues restent les Bi, les facteurs de forme Fij sont les mêmes dans les 3 systèmes en revanche les ρi et les Ei changent. Les ρi sont les réflectivités des surfaces et caractérisent la réflexion diffuse. Ils s'apparentent donc aux classiques coefficients de diffusion rouge, vert et bleu. Les Ei sont les émissions intrinsèques des surfaces et caractérisent l'énergie émise qui peut donc être colorée.
3. Exemples
Les images ci-dessous présentent une scène composée de :
- un grand cube sans face avant,
- un petit cube central.
Les 6 faces du cube central sont émettrices intrinsèques de lumière blanche et ont une réflectivité nulle (elles ne renvoient rien). Les 5 faces
modélisant le grand cube n'émettent aucune lumière intrinséquement et ont des réflectivités non nulles responsables des couleurs principalement
visibles sur les images.

Radiosité avec affichage par Z-Buffer et ombrage plat
Claire visualisation des surfaces élémentaires de décomposition des objets

Radiosité avec affichage par Z-Buffer et ombrage de Gouraud
Masquage des facettes
Image très similaire à ce qui aurait été obtenu en utilisant un Z-Buffer+Gouraud classique
et en remplaçant le cube central par une lumière ponctuelle

Changement des "couleurs" des faces du grand cube
Mise en évidence de réflexions colorées au niveau des jointures
entre la face bleue et les faces blanches
et entre la face rouge et les faces blanches

Nouveau changement de couleur
pour les faces inférieure et supérieure du grand cube
Qualité de l’affichage
On obtient une très bonne estimation des flux d'énergie à l'intérieur de la scène.
-> Des images très réalistes du point de vue des éclairages sont créées.
Le calcul de l’équilibre énergétique intègre de manière très précise le calcul de la composante de lumière ambiante de chaque surface, ce qui conduit généralement à des lumières douces qui semblent tamisées (résolution des problèmes d'illumination locale inhérents aux autres algorithmes de rendu). Les scènes d'intérieur tirent un grand profit de ce type de rendu.
La réalisation de l'algorithme d'affichage (par exemple un Z-Buffer associé à un lissage de Gouraud) renforce encore ce phénomène.
On modélise les ombres portées car on gère les occultations entre objets.
Rapidité de calcul
Une fois l’équilibre énergétique calculé, l’affichage d’une scène est très rapide (rapidité du Z-Buffer ou du lancer de rayons).
Contrairement au lancer de rayons, on n’a pas à recalculer l’équilibre si on effectue un déplacement de l'observateur à l’intérieur de la scène. Tant que la scène n’est pas modifiée, les calculs d’animation sont extrêmement rapides.
Qualité de l’affichage
Cet algorithme ne tient compte que de la lumière "diffusée". Il ne peut pas rendre compte des transmissions et des réflexions spéculaires.
La discrétisation de la scène et des calculs de facteurs de forme par méthode de l'hémisphère ou l'hémicube fait que certains problèmes d'aliasage
peuvent apparaître entraînant des problèmes comme par exemple sur les ombres :
- bords trop flous et/ou crénelés,
- ombres portées absentes pour les objets trop minces,
ou sur les éclairages :
- mauvais éclairage de certaines zones (apparition de motifs en "taches de léopard"),
- manque de précision sur l'éclairage des objets placés près de l'observateur et donc apparaissant gros à l'écran.
Rapidité de calcul
Les deux phases (a) de calcul des facteurs de forme et (b) de résolution du système d’équations linéaires demandent des quantités de calcul importantes. La phase de calcul des facteurs de forme est généralement la plus longue.
Plus on veut un résultat proche de la réalité, plus la discrétisation de la scène doit être poussée et donc plus le temps de calcul est important.
De plus, on est confronté à la résolution successive de deux problèmes, un en n2 du nombre de facettes et un en n3 du nombre
de facettes :
- n2 : calcul et le stockage des n2 facteurs de forme,
- n3 : résolution du système de n équations linéaires.
6. Améliorations
Contrôle des temps de calcul : radiosité progressive
Le problème de structure de données en n2 trouve une solution avec la technique de radiosité progressive. Cette technique apporte aussi une solution partielle au problème de temps de calcul cubique nécessaire à la résolution du système d'équations linéaires.
Cette technique permet de résoudre progressivement le système d'équations linéaires sans stockage de l'ensemble de la matrice des facteurs de forme. On ne la calcule que ligne par ligne au moment où chaque ligne est utilisée lors de la résolution du système d'équations linéaires par une méthode itérative.
L'algorithme est donc itératif, basé sur une boucle pseudo-infinie. Il traite les surfaces de la scène les unes après les autres pour évaluer et
affecter l'énergie qu'elles émettent vers les autres surfaces.
Une énergie déjà émise n'a plus à être émise.
-> On utilise un tableau B pour stocker les radiosités en cours de calcul, mais aussi un second tableau DB pour stocker les portions de ces radiosités
qui n'ont pas encore été émises vers les autres surfaces (créées, depuis la dernière émission, par réception depuis les autres facettes puis réémission).
Algorithme
La valeur n est le nombre de surfaces à traiter par radiosité.
Déclarer un tableau d'énergie B destiné à contenir la radiosité
de chacune des n surfaces
Déclarer un tableau d'énergie DB destiné à contenir l'énergie restant à émettre par chacune des n surfaces (énergie reçue depuis la dernière
émission)
Initialiser B et DB avec les valeurs d'énergie émise intrinsèquement par chaque surface
Faire
Choisir une surface F parmis les n surfaces (par exemple celle présentant la valeur DB maximale)
Calculer le tableau de facteurs de forme FF associé à F
// Allouer la fraction d'énergie émise par F à chacune des autres facettes
pour chaque surface FA
// Calculer l'énergie reçue par FA de la facette F et réémise
DR = roFA * DB[F] * FF[FA] * AF / AFA
// Incrémenter les tableaux DB et B avec l'énergie réémise par FA
DB[FA] += DR
B[FA] += DR
fin pour
// Mettre à 0 l'énergie restant à émettre par la surface f
DB[F] = 0
Calculer l'image correspondant aux n surfaces affectées des radiosités stockées dans B
Tant que l'image n'est pas satisfaisante
La ligne importante dans l'algorithme ci-dessus est la ligne DR = roFA * DB[F] * FF[FA] * AF / AFA qui permet de calculer et de stocker dans DR la quantité d'énergie reçue par la facette FA depuis la facette F puis réémise. roFA est la réflectivité de la facette FA. DB[F] est la quantité d'énergie restant à éméttre par la facette F. FF[FA] est le facteur de forme définissant la proportion d'énergie qui, émise par la facette f, est reçue par la facette FA. AF et AFA sont les surfaces des facettes F et FA.
On sait que cette technique de résolution permet la convergence vers la solution d'équilibre énergétique. Un problème est que le temps de convergence n'est pas prévisible. Un contrôle offert par cet algorithme concerne le choix de la surface F émettrice à chaque itération. On accélère la convergence en choisissant la surface possédant la radiosité maximale parmi celles restant à émettre.
Remarque: Au cours de l'exécution on peut être appelé à calculer plusieurs fois la même ligne de facteurs de forme à peu d'itérations d'écart. Cette source d'inoptimisation peut-être contrée en gardant en cache un certain nombre des lignes dernièrement calculées.


Radiosité progressive
Convergence vers l'image définitive
Limitation des problèmes d'aliasage : Discrétisation adaptative
On peut limiter les problèmes d'aliasage en utilisant une technique de discrétisation de la scène permettant d'augmenter la précision (augmenter
le nombre de surfaces) dans les zones critiques. La technique généralement employée consiste à subdiviser récursivement les surfaces.
On pourra détecter ces zones critiques par le fait que deux surfaces voisines situées à leurs limites présentent des valeurs Fdi-j différant
d'une valeur supérieure à une limite prédéfinie.

Une cathédrale

Une usine
La technique de calcul de l'illumination globale permet de calculer au mieux la composante de lumière ambiante due aux réflexions diffuses multiples (infinies) générées sur chaque surface diffusante d'une scène. Elle permet l'obtention d'images de très bonne qualité aux lumières douces telles qu'elles apparaissent très souvent dans la réalité quand les éclairages sont indirects ou diffus.
Cet effet est renforcé par la définition, contrairement au lancer de rayons et au Z-Buffer, de sources lumineuses non ponctuelles (surfaces lumineuses) et par la réalisation de lissages sur les couleur par l'algorithme d'affichage.
L'obtention d'images photoréalistes se heurte à l'impossibilité de modéliser les réflexions spéculaires et les transmissions.
Une technique fréquement employée pour obtenir des images de grande qualité consiste à faire précéder un rendu par lancer de rayons, d'une phase de calcul des radiosités permettant une évaluation correcte des éclairages ambiants.
Un autre inconvénient des calculs de radiosité est la lenteur.