Le rendu par lancer de rayons
(ray tracing)
0. Problématique
Les techniques de rendu décrites jusqu'à présent visant à afficher à l'écran des scènes composées d'objets et de sources lumineuses (le
Z-Buffer pour l'élimination des parties cachées, Lambert + Gouraud ou Lambert + Phong pour les calculs d'illumination) ont l'inconvénient
principal de ne pas permettre d'obtenir des images d'un grand réalisme. Ces techniques n'ont pas été conçues dans cet objectif, mais
plutôt dans un but de rapidité d'exécution au prix d'un réalisme moyen.
Si le but est d'améliorer la qualité des images produites, une solution peut être d'utiliser l'algorithme de rendu par lancer de rayons.
Ses principales caractéristiques de rendu sont :
- l'élimination intrinsèque des parties cachées,
- la modélisation des réflexions diffuses,
- la modélisation des réflexions spéculaires,
- la modélisation des transmissions (réfractions),
- la réflexion des objets les uns sur les autres,
- la création intrinsèque des ombres portées.
Les trois dernières de ces caractéristiques sont nouvelles et nous manquaient pour aller vers le photo-réalisme des images générées.
1.1. Introduction
On sait que notre oeil est principalement constitué d'une rétine, d'un cristallin, d'une pupille et d'un iris. Les rayons lumineux
provenant de l'extérieur de l'oeil (provenant de la scène regardée) traversent l'iris dont le diamètre est contrôlé par la pupille, sont
focalisés par le cristallin vers la rétine où ils viennent exciter des cellules photoréceptrices de lumière (des "bâtonnets" qui captent
l'intensité de lumière et des "cônes" qui captent la couleur) qui transforment le signal lumineux reçu en un signal chimico-électrique
transmis au cerveau par le nerf optique. On pourrait dire que les rayons lumineux créent une image sur la rétine qui est saisie et envoyée au cerveau.
Pour déterminer comment cette image est créée sur la rétine on doit déterminer comment sont créés les rayons lumineux qui la créent. On va
donc suivre en sens inverse le parcours de chaque rayon lumineux qui s'imprime sur la rétine de l'observateur pour déterminer l'ensemble
des phénomènes qui concourent à sa création et ainsi déterminer ses caractéristiques précises. Une partie de la difficulté de cette méthode est que
beaucoup de phénomènes peuvent créer un rayon lumineux, que plusieurs phénomènes peuvent s'additionner pour créer ce rayon lumineux et que, parmi
ces phénomènes, un certain nombre sont liés à l'existence d'autres rayons lumineux dont il faudra déterminer les caractéristiques. Dit autrement,
un rayon peut être créé à partir de plusieurs rayons lumineux qui eux-mêmes peuvent être créés à partir de plusieurs rayons lumineux et ainsi de
suite "récursivement". Une bonne analogie serait celle consistant à déterminer les caractéristiques d'un fleuve se jetant dans l'océan
en remontant depuis l'exutoire jusqu'à leurs sources l'intégralité des rivières participant à sa création.
1.2. Formalisation
Pour la génération d'images la formalisation de cette technique consiste :
- à placer l'observateur,
- à placer un écran virtuel entre l'observateur et la scène à visualiser,
- pour chaque pixel de l'écran virtuel, à suivre la trajectoire rectiligne partant de l'observateur et traversant ce pixel,
- à "entrer" dans la scène selon cette trajectoire rectiligne de façon à déterminer quels phénomènes ont pu créer le rayon
lumineux de parcours inverse, et par ce biais, déterminer les caractéristiques chromatiques de ce rayon lumineux et donc du pixel initialement
traversé.

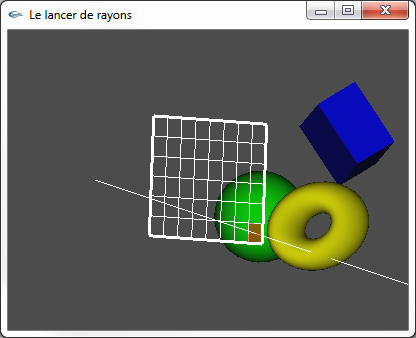
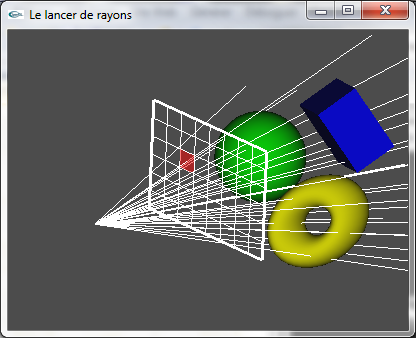
Parcours des trajectoires rectilignes de l'observateur vers la scène
correspondant aux parcours inverses des rayons lumineux
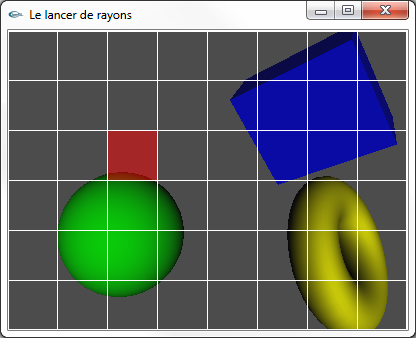
On traite le rayon "primaire" partant de l’observateur et passant par chaque pixel de l'écran virtuel de manière à déterminer la couleur attribuée à ce pixel.
| Un rayon primaire par pixel de l'écran virtuel |
|
|
|
Enter pour switcher entre les affichages |
Deux cas sont possibles lors du parcours d'un rayon primaire dans une scène :
(1) Aucun objet n'est intercepté par le rayon.
-> La "couleur" du rayon et donc celle du pixel lui correspondant, est la couleur du fond (noir ou autre couleur choisie arbitrairement).
(2) Un ou plusieurs objets sont interceptés par le rayon.
- On trouve l'objet dont l'intersection avec le rayon est la plus proche de la source du rayon (l'observateur).
- En fonction des caractéristiques de cet objet vis à vis de la lumière, la "couleur" du rayon est calculée
par somme, si elles existent, des composantes de lumière (a) diffusée, (b) réfléchie spéculairement et (c) transmise
par l'objet au point d'intersection. On évalue ainsi comment le rayon a pu être créé par recomposition à partir de ces trois composantes.

Reconstitution du rayon lumineux inverse d'un rayon primaire
à partir d'une (ou plusieurs) réflexion diffuse, d'une transmission et d'une réflexion spéculaire
intervenant au niveau du point d'intersection entre le rayon primaire
et le premier objet qu'il rencontre
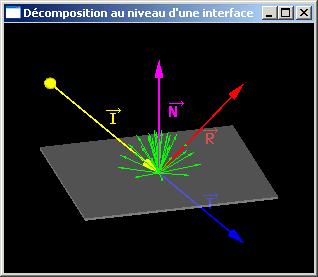
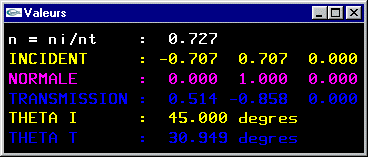
Ces composantes sont la conséquence du phénomène optique de décomposition de la lumière lorsque celle-ci change de milieu de propagation et, provenant
d'un milieu I (milieu d'incidence), rencontre un milieu T (milieu de transmission) au niveau de l'interface entre ces deux milieux. Un
rayon incident crée ainsi un certain nombre de composantes par :
- réflexion diffuse dans le milieu I,
- réflexion spéculaire dans le milieu I,
- transmission dans le milieu T (réfraction),
- réflexion diffuse dans le milieu T,
- absorption par les milieux I et T (transformation en chaleur, changement de longueur d'onde),
- ...
En lancer de rayon seules les trois premières de ces composantes sont effectivement gérées, la quatrième est ignorée ou plus exactement est assimilée
à la 5ème qui n'est pas gérée au sens stricte du terme car elle se caractérise simplement par la disparition d'une "partie" du
rayon incident.
|
Phénomène optique réel de décomposition d'un rayon lumineux incident (jaune) au niveau de l'interface entre deux milieux en un rayon réfléchi (rouge), un rayon transmis (bleu) et de la lumière diffusée (vert) |
|
|
|
n, N, m et M pour modifier le facteur n = ni/nt |
Précision : Dans ce chapitre, seule la réflexion spéculaire parfaite est considérée. L'existence éventuelle de cônes de réflexion spéculaire implantés sur les points d'incidence et ouverts autour des axes privilégiés de réflexion spéculaire n'est pas abordée. Les images ainsi obtenues ne montreront pas de taches de réflexion spéculaire généralement constatées comme étant de la couleur des sources lumineuse. Le seul résultat obtenu par gestion de cette caractéristique sera l'apparition de reflets des objets les uns sur les autres. Les transmissions étant elles aussi géométriquement parfaites, le seul phénomène pouvant expliquer la couleur adoptée par un objet sera la réflexion diffuse.
1.3. Caractérisation des rayons, des milieux et des interfaces entre milieux
Les rayons sont définis par deux caractéristiques géométriques principales :
- Point d'émission
- Direction d'émission
Ces caractéristiques géométriques permettent en particulier de réaliser les calculs d'intersection objet-rayon et les calculs de directions de
réflexion et de transmission.
Les milieux sont généralement définis a minima par la caractéristique suivante :
- Indice de réfraction (voir plus loin)
Les milieux faisant partie des objets, les indices sont généralement associés aux objets. A noter : Il existe un milieu inter-objets qui est généralement
considéré comme vide et qui possède donc l'indice de réfraction du vide : 1.0 même si ce milieu n'appartient explicitement à aucun objet.
D'autres caractéristiques peuvent être ajoutées :
- Atténuation de la lumière en fonction de la distance qu'elle parcourt dans le milieu
- ...
Les interfaces entre milieux sont généralement définies a minima par les caractéristiques suivantes :
- Coefficients RVB de diffusion (proportions RVB de la lumière reçue qui sont réfléchies par diffusion dans le milieu incident)
- Coefficients RVB de réflexion spéculaire (proportions RVB de la lumière reçue qui sont réfléchies spéculairement dans le milieu incident)
- Coefficients RVB de transmission (proportions RVB de la lumière reçue qui sont transmises par réfraction dans le milieu de transmission)
La somme de ces 3 coefficients RVB est obligatoirement inférieure ou égale à 1.0 en rouge en vert et en bleu.
Les interfaces faisant partie des objets, les coefficients RVB ci-dessus sont généralement associés aux objets.
D'autres caractéristiques peuvent être ajoutées :
- Réflectivité si on gère des réflexion spéculaires non parfaites
- ...
1.4. Récursivité
Chaque intersection entre un rayon et un objet entraîne le calcul de l'ensemble des rayons ayant pu générer ce rayon (diffusions, réflexion spéculaire,
transmission) qui entraîne le calcul de l'ensemble des rayons qui ont pu générer ces rayons qui entraîne le calcul de l'ensemble des rayons
qui ont pu générer ces rayons et ainsi de suite.
-> On est en présence d'un phénomène intrinsèquement récursif.
-> On programme un algorithme récursif.
On classifie les rayons en fonction de leur "rôle" au sein de la récursivité :
- Un rayon "primaire" est un rayon qui a été émis au départ en position de l'observateur et qui traverse un pixel de l'écran
virtuel de projection.
- Un rayon "secondaire" est un rayon issu d'un phénomène de réflexion spéculaire ou de transmission. Son point d'émission
est une intersection objet-rayon. Sa direction est calculée au moyen des formules mathématiques appropriées (voir plus
loin).
- Un rayon d'ombre est un rayon issu d'un phénomène de réflexion diffuse. Son point d'émission est une intersection objet-rayon.
Il est dirigé en direction d'une source lumineuse. Il s'appelle rayon d'ombre car, outre le calcul de diffusion, il a pour but de déterminer
si le point d'intersection est éclairé ou non par la source lumineuse, c'est dire n'est pas masqué par l'objet lui-même ou un autre
objet. C'est ce test qui a pour conséquence la gestion intrinsèque des ombres portées.
Algorithmiquement la récursivité est amorcée sur un rayon primaire que l'on qualifie de niveau 1 qui entraîne potentiellement des appels récursifs
sur des rayons secondaires de réflexion ou de transmission que l'on qualifie de niveau 2 qui entraînent potentiellement des appels récursif sur
des rayons secondaires de réflexion ou de transmission de niveau 3 qui entraînent potentiellement des appels récursifs sur des rayons secondaires
de réflexion ou de transmission de niveau 4 et ainsi de suite. A chaque niveau de récursivité, des rayons d'ombre sont tracés vers les sources
lumineuses pour évaluer des diffusions. Ces rayons ne sont pas générateurs d'appels récursifs.
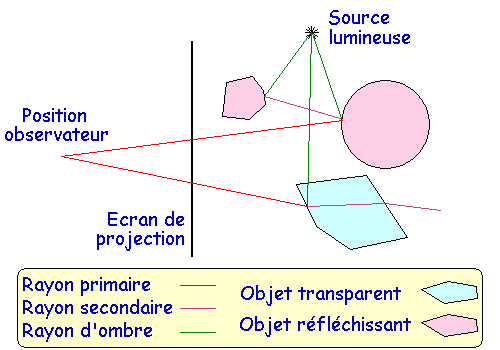
Gestion de rayons primaires, de rayons secondaires et de rayons d'ombre
2. Calcul des différentes composantes
On considère un rayon incident I présentant une intersection P avec un objet O. L'objet O et le rayon I permettent de calculer la position de P.
(a) Pour calculer la valeur diffusée en P on doit :
- lancer un rayon d'ombre de P vers chacune des sources lumineuses S présentes dans la scène pour déterminer si ce rayon est
intercepté ou non par un objet (à l'ombre ou non),
- pour chaque rayon non intercepté, calculer la lumière diffusée en P sous éclairage de la source S en appliquant une formule adaptée
à ce calcul (loi de Lambert ou autre) et donc en utilisant des coefficients de diffusion de l'objet O,
- sommer le résultat de chacun de ces calculs pour obtenir la quantité globale de lumière diffusée au point P.
(b) Pour calculer la valeur de la composante de réflexion spéculaire en P on doit :
- calculer les caractéristiques chromatiques du rayon réfléchi en lançant récursivement l'algorithme de lancer de rayons sur le rayon
secondaire défini avec pour origine le point P et pour direction la direction de réflexion
![]() du rayon I (voir ci-dessous),
du rayon I (voir ci-dessous),
- pondérer la valeur obtenue ci-dessus par les coefficients de réflexion spéculaire de l'objet.
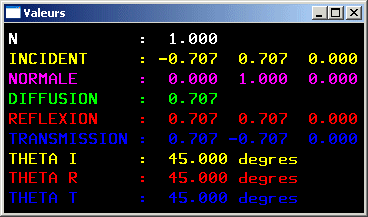
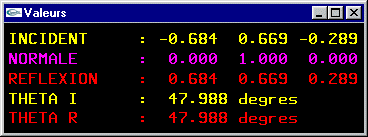
Calcul de la direction de réflexion
![]() :
:
-
![]() est la direction d'incidence, c'est à dire la direction normée de P à la source du rayon incident.
est la direction d'incidence, c'est à dire la direction normée de P à la source du rayon incident.
-
![]() est la normale à l'interface au niveau du point P orientée dans le milieu incident.
est la normale à l'interface au niveau du point P orientée dans le milieu incident.
- θi est "l'angle d'incidence" c'est à dire l'angle entre
![]() et
et
![]() .
.
- θr est angle de réflexion, c'est à dire l'angle existant entre
![]() et
et
![]() .
.
La direction de réflexion
![]() est la direction qui vérifie les deux propriétés suivantes (loi de Snell-Descartes) :
est la direction qui vérifie les deux propriétés suivantes (loi de Snell-Descartes) :
-
![]() ,
,
![]() et
et
![]() sont dans le même plan.
sont dans le même plan.
- θr = -θi.
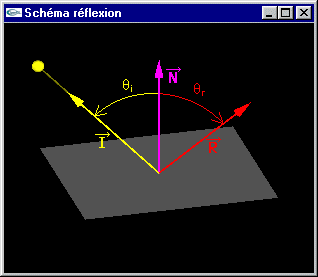
|
Calcul des caractéristiques géométriques d'un rayon réfléchi (rouge) à partir d'un rayon incident (jaune) |
|
|
|
1, 2, 3, 4, 5 et 6 pour modifier la position de la source (sphère jaune) du rayon incident Touches de curseur et souris pour manipuler la scène |
Les rayons secondaires de réflexion sont exclusivement tracés dans le milieu inter-objets.
(c) Pour calculer la valeur de la composante de transmission en P on doit :
- calculer les caractéristiques chromatiques du rayon transmis en lançant récursivement l'algorithme de lancer de rayons sur le rayon
secondaire défini avec pour origine le point P et pour direction la direction de transmission
![]() du rayon I (voir ci-dessous),
du rayon I (voir ci-dessous),
- pondérer la valeur obtenue ci-dessus par les coefficients de transmission de l'objet.
Calcul de la direction de transmission
![]() :
:
-
![]() est la direction d'incidence, c'est à dire la direction normée de P à la source du rayon incident.
est la direction d'incidence, c'est à dire la direction normée de P à la source du rayon incident.
-
![]() est la normale à l'interface au niveau du point P orientée dans le milieu incident.
est la normale à l'interface au niveau du point P orientée dans le milieu incident.
- θi est "l'angle d'incidence" c'est à dire l'angle entre
![]() et
et
![]() .
.
- θr est "l'angle de transmission" c'est à dire l'angle entre -![]() et
et
![]() .
.
- ni est l’indice de réfraction du milieu dans lequel se propage le rayon incident.
- nt est l’indice de réfraction du milieu dans lequel se propage le rayon transmis.
La direction de réflexion est la direction qui vérifie les deux propriétés suivantes (loi de Snell-Descartes) :
-
![]() ,
,
![]() et
et
![]() sont dans le même plan.
sont dans le même plan.
- ni sin(θi) = nt sin(θr)
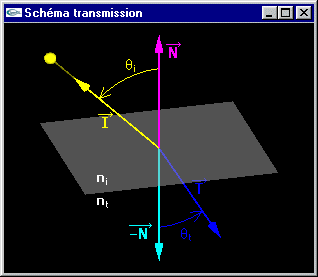
|
Calcul des caractéristiques géométriques |
|
|
|
n, N, m et M pour modifier le facteur n = ni/nt 1, 2, 3, 4, 5 et 6 pour modifier la position de la source (sphère jaune) du rayon incident Touches de curseur et souris pour manipuler la scène |
Attention, les rayons secondaires de transmission sont tracés dans le milieu inter-objets mais aussi dans les objets "transparents".
-> Cette caractéristique contraint le programmeur à gérer l'entrée des rayons dans les objets et leur sortie.
La conséquence sera probablement d'avoir à ajouter aux caractéristiques de chaque rayon la valeur de l'indice de réfraction du milieu dans
lequel il se propage.
Remarque : En fonction de ni, nt et θi, la valeur de θt peut ne pas être calculable. Ce cas est susceptible de se produire lorsque nt est plus petit que ni. En effet ni/nt est alors plus grand que 1.0, et ni/nt*sin(θi) sera alors plus grand que 1.0 au delà de la valeur limite de θi = asin(nt/ni) rendant impossible l'utilisation de l'arc sinus sur cette valeur pour le calcul de θt. Dans ce cas il n'y a pas de transmission et une réflexion totale. Il est à signaler que dans cette situation, quand il existe, θt est forcément plus grand que θi.
| Matériel | Indice |
| Vide | 1.0 |
| Air | 1.000293 |
| Eau | 1.33 |
| Verre | 1.5 |
| Diamant | 2.42 |
Indices de réfractions de matériaux courants
Valeurs variables en fonction de la température
et de la longueur d'onde (jaune dans le tableau)
3. Algorithme simplifié
L'algorithme proposé ici se compose d'une fonction principale et d'une fonction utilitaire récursive.
La fonction principale a pour but de créer une image. Les paramètres de cette fonction sont l'observateur (défini par sa position et par son
écran virtuel de visualisation, appelé écran ci-dessous) et la scène visualisée (composée d'objets et de sources lumineuses). Elle calcule l'ensemble
des rayons primaires, lance sur chacun d'eux le calcul de lancer de rayon via la fonction utilitaire récursive et affecte la couleur obtenue
au pixel correspondant de l'image.
La fonction utilitaire réalise le lancer de rayon d'un seul rayon (primaire ou secondaire) et retourne la "couleur" de ce rayon (on
pourrait parler d'énergie colorée de ce rayon). Ses paramètres sont le rayon à traiter et la scène où le rayon sera propagé.
/* Calcul et retour d'une image au moyen
*/
/* de l'algorithme de lancer de rayons */
/* s : La scene visualisée */
/* (composée d'objets et de lumières) */
/* o : L'observateur visualisant la scène */
/* (défini par sa position */
/* et les caractéristique de son écran */
/* virtuel de visualisation) */
Image lancerDeRayons(Scene s,Observateur o)
Image image <- créer image de résolution égale
à celle de l'écran de o
pour chaque pixel p d'indice (l,c) de l'écran de o
Rayon r <- rayon passant par l'observateur et par p
image[l][c] <- lancerRayon(s,r)
finpour
finfonction
/* Calcul et retour de la couleur */
/* d'un rayon au moyen de l'algorithme */
/* de lancer de rayons
*/
/* s : La scène traversée */
/* (composée d'objets et de lumières) */
/* r : Le rayon
*/
/* (caractérisé par un point d'émission */
/* et une direction)
*/
Couleur lancerRayon(Scene s,Rayon r))
Objet o <- objet de s dont l'intersection avec r
est la plus proche de la source de r
si o n'existe pas
retourner noir
sinon
Point p <- point d'intersection entre r et o
Rayon rr <- rayon réfléchi de r en p sur o
Coefficients kr <- coefficients de réflexion de o
Couleur cr <- lancerRayon(s,rr) * kr
Rayon rt <- rayon transmis de r en p vis à vis de o
Coefficients kt <- coefficients de transmission de o
Couleur ct <- lancerRayon(s,rt) * kt
Couleur cd <- noir
pour chaque lumiere sl de s
Rayon rd <- rayon de p vers sl
si rd non intercepté par un objet de s
cd <- cd+diffusion(sl,o,rd)
finsi
finpour
retourner cr+cd+ct
finsi
finfonction
4. Inconvénients du lancer de rayons
Quantité de calculs et temps d'exécution
Les calculs implantés sont obligatoirement réalisés en utilisant des variables réelles et font appel à des opérations mathématiques non triviales
réalisées en grand nombre.
-> Les temps d'exécution sont intrinsèquement longs.
Exemple : Tester l'existence d'une intersection entre un rayon et une scène composée de 1000 objets et, si cette intersection existe,
déterminer quel est l'objet le plus proche de la source du rayon demande 1000 tests d'intersection élémentaires rayon-objet. Si on souhaite
calculer une image de cette scène composée de 1 million de pixels (résolution de 1000 sur 1000), la gestion du million de rayons primaires demandera
1000x1000000 = 1 milliard de tests d'intersection élémentaires. Si un test d'intersection élémentaire demande en moyenne 100 opérations mathématiques
élémentaires, le nombre total d'opérations pour une seule image est de 100 milliards.
Remarque : Dans l'exemple ci-dessus, seuls les rayons primaires ont été gérés, les rayons secondaires n'ont pas été considérés c'est
à dire que la récursivité n'a été lancée sur aucun rayon primaire.
Remarque : Dans l'exemple ci-dessus, et d'une manière générale quand on utilise le lancer de rayons, on fait exactement ce que l'on
a dit que l'on ne ferait pas pour l'implantation du Z-Buffer parce que cela risquait fort d'entraîner des temps de calcul très longs
et un gaspillage de ressources CPU.
Récursivité et temps d'exécution
A chaque interception d'un objet par un rayon primaire ou secondaire (rayon de niveau de récursivité n avec n = 1 pour primaire, avec n > 1 pour
secondaire), outre les rayons d'ombre, on lance potentiellement deux rayons secondaires (de niveau n+1) : un rayon pour la gestion de la transmission
et un rayon pour la gestion de la réflexion spéculaire.
-> On peut assister à une explosion exponentielle du nombre total de rayons tracés à l'intérieur de la scène.
Si nMax est le niveau de profondeur maximum de la récursivité, il y a au maximum de l'ordre de 2nMax rayons tracés
pour chaque pixel.
Pour obtenir un certain réalisme, le niveau de récursivité doit être poussé assez loin (au moins 8, habituellement
10 à 12 voire 14) et donc les temps de calcul peuvent être très longs (plusieurs heures par image pour des scènes complexes).
Exemple : L'exemple du paragraphe précédent (1 millions de pixels, 1000 objets) est repris en gérant cette fois une récursivité de niveau
nMax = 10. On a 2nMax = 1024 ≈ 1000. On donc a potentiellement de l'ordre de 1000x1000000 = 1 milliards de rayons primaires et secondaires
tracés. Avec 100000 opérations arithmétiques par rayon, on arrive à 100000 milliards d'opérations arithmétiques par image.
Calcul d'illumination et qualité/réalisme du résultat
L’illumination est "moyennement" locale. Toute illumination provient d’une diffusion sous l'éclairage d'une source de lumière
répertoriée comme telle soit de façon directe, soit de façon indirecte après un nombre de réflexions spéculaires ou de
transmissions successives au plus égal au niveau de profondeur de récursivité maximum nMax utilisé. Cela signifie que tout point
"situé" à plus de nMax réflexions ou transmissions d'une diffusion sera de la couleur du fond et donc invisible. Dans la réalité les
réflexions et transmissions sont infinies et concourent à l'existence d'une certaine quantité de lumière ambiante éclairant tous les
objets de la scène.
-> Le rendu d'une scène par lancer de rayons peut faire apparaître des objets non éclairés alors qu'ils auraient dû l'être
un peu.
Ce problème peut être partiellement résolu en attribuant une composante de lumière ambiante à chacun des objets de la scène. Cette composante est
souvent définie avec une valeur constante car on ne sait pas la calculer, et est ajoutée aux autres.
L'algorithme de lancer de rayons ne modélisant que très imparfaitement les transferts d'énergie (la notion d'énergie par unité de surface n'est pas modélisée), il ne peut pas restituer de "caustique". Les caustiques sont les motifs qui apparaissent sur une surface éclairée par de la lumière transmise à l'intérieur d'un objet à surface courbe et subissant ainsi une concentration ou une atténuation énergétique. Un exemple classique de caustique est la concentration de la lumière opérée par une loupe qui conduit à l'apparition d'une zone sur-éclairée. Un autre exemple est l'ensemble des motifs mouvants qui apparaissent au fond d'une piscine lorsque la surface de celle-ci est perturbée.

Réfraction de la lumière au fond d'une piscine
(http://photos.massal.net/swimming-pool/swimming-pool-deep-blue-water-caustics-california-p.html)
On ne peut pas restituer la diffusion de la lumière dans les matériaux (en particulier l’air).
-> Certains éclairages peuvent être non réalistes car pas assez diffus.
-> Certaines ombres peuvent être non réalistes car elles présenteront des bords trop nets.
5. Objets et lumières utilisables
Deux questions n'ont pas été posées jusqu'à présent :
- Quels sont les types d'objet qui peuvent être représentés en lancer de rayons ?
- Quels sont les types de lumière qui peuvent être placés dans les scènes affichées en lancer de rayons ?
La réponse à la première question requière de répondre à une autre question : Quelles sont les opérations qui doivent être implantées pour chaque
type d'objet pour que les objets de ce type puissent être manipulés au sein d'un algorithme de lancer le rayons ?
L'implantation de deux opérations est nécessaire auxquelles on peut en ajouter une troisième corrélée à la première :
- test d'intersection objet-rayon,
- détermination de la normale à un objet en n'importe lequel des points de sa surface,
- détermination de la position de l'intersection entre un objet et un rayon.
Ces opérations sont essentiellement mathématiques et nécessitent de disposer d'équations permettant de représenter mathématiquement les objets
(et les rayons). On peut donc dire que n'importe quelle classe d'objet modélisable au moyen d'équations mathématiques est utilisable
en lancer de rayons (quelques exemples ci-dessous) :
- sphère,
- cube,
- cône,
- tore,
- surfaces contrôlées (surface paramétrique bicubique, quadrique, ...),
- …
Bien entendu, on peut aussi utiliser des ensembles de facettes même si ce n'est pas recommandé car ces ensembles sont généralement de tailles
importantes avec pour conséquence un fort impact sur la rapidité du calcul de lancer de rayon.
La réponse à la seconde question est plus simple. L'algorithme du lancer de rayons utilise des rayons caractérisés par un point d'émission
et une direction d'émission. Toutes ces caractéristiques sont parfaitement compatibles avec les types de lumière :
- ponctuelle,
- directionnelle,
- spot.
6. Avantages du lancer de rayons
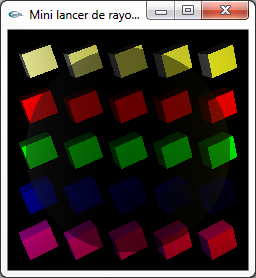
Réalisme
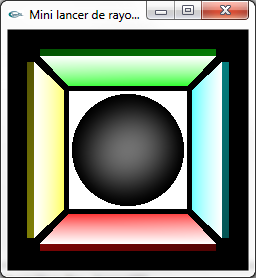
Des effets tels que les réflexions spéculaires et les transparences sont restitués intrinsèquement. Aucun autre algorithme n'est capable de modéliser ces effets de manière aussi satisfaisante.
|
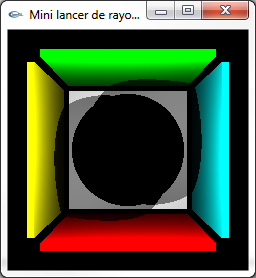
Comparaison entre affichages OpenGL et lancer de rayons |
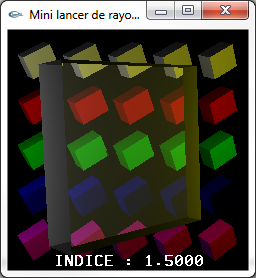
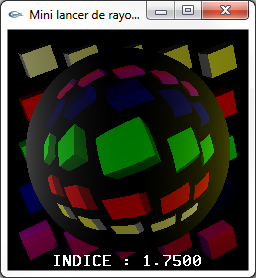
||
|
Meilleure gestion géométrique des transparences |
||
|
Enter pour amorcer le calcul de l'image |
Les parties cachées sont éliminées de manière intrinsèque. Au niveau 1 de la récursivité, on est en présence d’un algorithme très voisin du Z-Buffer dans ses résultats : le Ray Casting.
Les ombres portées sont intrinsèques au modèle.
Objets non facettisés
Un point particulier très avantageux est que, contrairement à ce qui est généralement nécessaire quand on utilise le Z-Buffer, il n'est pas obligatoire
de décomposer les objets de la scène en facettes triangulaires ou en surfaces élémentaires planes.
Les artefacts d'affichage liés à cette décomposition disparaissent :
- visualisation des facettes sur les objets courbes à cause de problèmes de coloriage même si les techniques de Gouraud ou de Phong sont utilisées,
- pour les objets courbes, silhouette polygonale au lieu de silhouette courbe,
- éclairage de mauvaise qualité quand les détails d'éclairage ont une taille inférieure ou voisine de la taille des facettes,
- rendu de mauvaise qualité quand on zoome,
- ...
Résoudre ces problèmes en Z-Buffer nécessitait souvent d'augmenter le nombre de facettes générées au fort détriment de la rapidité d'affichage.
Algorithme facilement parallélisable
Les rayons primaires correspondant aux pixels de l'image à calculer sont indépendants les uns des autres. Il est donc possible de les distribuer
à différents processeurs pour que chacun d'eux calcule une partie des pixels de l'image.
On obtiendra assez naturellement un équilibrage de charge de calcul entre les processeurs en effectuant la distribution de façon entrelacée statique
ou dynamique. Par exemple si on dispose de 4 processeurs, on pourra distribuer statiquement les pixels de coordonnées (l,c) aux processeurs selon
le schéma décrit dans le tableau suivant :
| l \ c | c%2 = 0 | c%2 = 1 | ||||
| l%2 = 0 |
|
|
||||
| l%2 = 1 |
|
|
Numéro de processeur affecté aux pixels
en fonction de leurs numéros de ligne et de colonne
Une autre façon d'implanter le parallèlisme sur les pixels consiste à réaliser l'affectation de façon dynamique. Les processeurs fonctionnent en mode client-serveur et reçoivent les rayons primaires (les pixels) un par un. Lorsqu'un processeur a calculé la couleur correspondant au rayon primaire qu'il a en charge, il notifie cette couleur comme résultat et se met en attente d'un autre rayon primaire. Le scheduler fonctionne en asynchrone pour l'envoi des rayons primaires aux processeurs et la réception des couleurs en résultat.
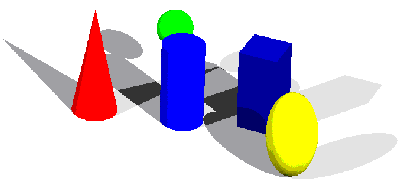
Création des ombres portées
Présence probable de trois lumières :
une lumière ponctuelle ou directionnelle puissante devant à droite
une lumière ponctuelle ou directionnelle moins puissante devant à gauche
une lumière ambiante

Des réflexions spéculaires
(sol, cylindre du milieu de l'image et parallélépipède rectangle à droite)

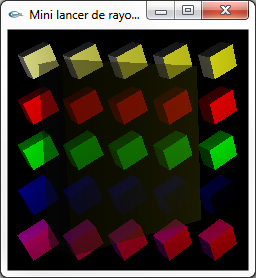
Des transmissions à travers des billes
d'indices de réfraction 1.333, 1.5, 2.5 et 4.0
(de gauche à droite et de bas en haut)
induisant soit un agrandissement soit un rétrécissement
de ce qui se trouve en arrière plan

Inversion des objets en arrière plan
7. Quelques problèmes mathématiques classiques
Calcul de la direction du rayon réfléchi
Soient :
-
![]() le vecteur normé incident,
le vecteur normé incident,
-
![]() le vecteur normé réfléchi,
le vecteur normé réfléchi,
-
![]() la normale à l’interface orientée dans le matériau où se propage le rayon incident.
la normale à l’interface orientée dans le matériau où se propage le rayon incident.
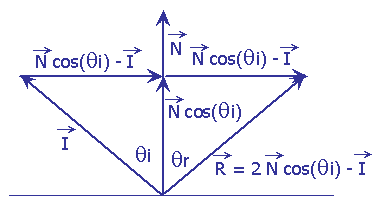
Calcul de la direction du rayon réfléchi
![]()
correspondant à la direction d'incidence
![]()
Sachant que abs(θi) = abs(θr), on établit :
![]() = 2
= 2
![]() cos(θi) -
cos(θi) -
![]()
puis
![]() = 2
= 2
![]() (
(![]() .
.![]() ) -
) -
![]()
en substituant le calcul cos(θi) avec le produit scalaire de
![]() et de
et de
![]() .
.
Calcul de la direction du rayon transmis
Soient :
-
![]() le vecteur normé incident,
le vecteur normé incident,
-
![]() le vecteur normé transmis,
le vecteur normé transmis,
-
![]() la normale à l’interface orientée dans le matériau
où se propage le rayon incident,
la normale à l’interface orientée dans le matériau
où se propage le rayon incident,
-
![]() le vecteur normé perpendiculaire à
le vecteur normé perpendiculaire à
![]() situé dans le plan déterminé par
situé dans le plan déterminé par
![]() et
et
![]() ,
,
- ni et nt les indices de réfraction des milieux d'incidence et de transmission.

Calcul de la direction du rayon transmis
![]()
correspondant à la direction d'incidence
![]()
On établit :
![]() et
et
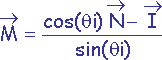
->
![]()
Si on pose n =
![]() , on obtient :
, on obtient :
![]() .
.
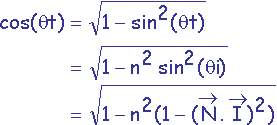 car
car
![]()
Ce qui nous conduit pour finir à :
![]()
qui ne contient que des quantités connues.
Calculs d'intersection
Intersection entre une sphère et un rayon
On désire connaître, si elle existe, la position de(s) l'intersection(s) entre un rayon lumineux et une sphère de rayon r centrée
sur l'origine. On sait qu'il y a trois possibilités :
- Il n'y a pas d'intersection.
- Il y a une seule intersection qui correspond au cas où le rayon tangente la sphère ou au cas où le rayon est émis depuis l'intérieur
de la sphère.
- Il y a deux intersections.
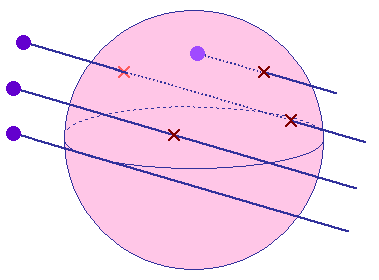
0, 1 ou 2 intersections entre un rayon et une sphère
Source en violet
Le système d'équations à résoudre est constitué de l'équation paramétrique de la demi-droite sous-tendue par le rayon lumineux et de l'équation cartésienne de la sphère :
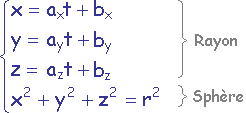 avec t ∈ ]0.0,+∞[
avec t ∈ ]0.0,+∞[
Dans le système d'équations ci-dessus, (bx,by,bz) est la position de la source du rayon, (ax,ay,az) est sa direction et r est le rayon de la sphère. x, y, z et t sont les inconnues qu'il convient de déterminer. Seule une valeur de t strictement positive correspondra à une intersection valide. C'est à dire que t ∈ ]0.0,+∞[ pour définir la demi-droite sous-tendue par le rayon.
Par substitution de x, de y et de z dans la 4ème équation avec les termes des 3 premières équations, on fait disparaître x, y et z et on obtient :
(axt + bx)2+(ayt + by)2+(azt + bz)2 = r2
puis (ax2+ay2+az2)t2 + 2(axbx+ayby+azbz)t
+ bx2+by2+bz2 = r2
On obtient donc une équation du second degré en t. Sa résolution conduit à l'obtention de 0, 1 ou 2 racines réelles positives ou nulles et donc
0, 1 ou 2 intersections entre le rayon et la sphère. Leurs positions peuvent être déterminées en réinjectant t dans le système d'équation paramétrique
du rayon.
Précision : S'il y a deux racines positives, celle de valeur minimale est celle qui est située le plus près de la source du rayon.
Intersection entre une facette triangulaire et un rayon
On désire connaître la position de l'intersection (si elle existe) entre un rayon et une facette triangulaire non dégénérée connue par
les coordonnées dans l’espace de ses trois sommets A, B et C. On sait qu'il y a trois possibilités :
- Il n'y a pas d'intersection lorsque :
- Le rayon est parallèle à la facette mais n'est pas dans le plan qu'elle sous-tend.
- Le rayon est parallèle à la facette, est dans le plan qu'elle sous-tend et ne coupe pas la facette.
- Le rayon n'est pas parallèle à la facette et ne coupe pas la facette.
- Il y a une infinité d'intersection lorsque :
- Le rayon est parallèle à la facette, est dans le plan qu'elle sous-tend et ne coupe pas la facette uniquement au niveau
des sommets A, B ou C.
- Il y a une seule intersection lorsque :
- Le rayon est parallèle à la facette, est dans le plan qu'elle sous-tend et coupe la facette uniquement au niveau des sommets
A, B ou C.
- Le rayon n'est pas parallèle à la facette et coupe la facette.
Les calculs ci-dessous s'intéressent uniquement au cas où le rayon n'est pas parallèle à la facette.
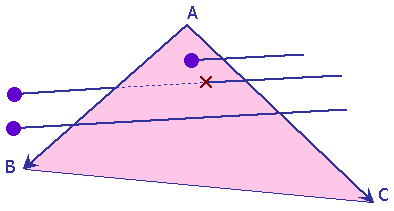
0 ou 1 intersection entre un rayon et une facette
Source en violet
Le système d'équations constitué des équations paramétriques de la facette et du rayon est construit puis résolu.
Les équations paramétriques de la facette sont définies à partir des positions
![]() ,
,
![]() et
et
![]() de ses 3 sommets.
de ses 3 sommets.
On calcule les vecteurs correspondant aux deux cotés
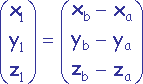 et
et
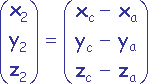 du triangle.
du triangle.
Le système d'équations paramétriques de la facette est donc
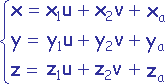 avec u >= 0, v >= 0 et u+v <= 1.0 (u et v sont les coordonnées
des points de la facette comptées dans le repère dont les axes sont les cotés AB et AC du triangle).
avec u >= 0, v >= 0 et u+v <= 1.0 (u et v sont les coordonnées
des points de la facette comptées dans le repère dont les axes sont les cotés AB et AC du triangle).
Les équations paramétriques du rayon sont définies à partir de sa direction
 et de la position de sa source
et de la position de sa source
 .
.
Le système d'équations paramétriques du rayon est
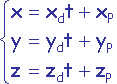 avec t > 0.0.
avec t > 0.0.
Le système global à résoudre est
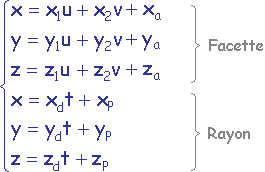 avec t > 0.0, u >= 0, v >= 0 et u+v <= 1.0.
avec t > 0.0, u >= 0, v >= 0 et u+v <= 1.0.
Par substitution le système devient
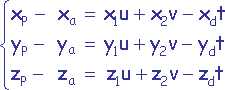 avec t > 0.0, u >=
0, v >= 0 et u+v <= 1.0.
avec t > 0.0, u >=
0, v >= 0 et u+v <= 1.0.
Si on pose x3=xp-xa, y3=yp-ya et z3=zp-za, le
système devient
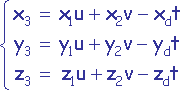 avec t > 0.0, u >= 0, v
>= 0 et u+v <= 1.0.
avec t > 0.0, u >= 0, v
>= 0 et u+v <= 1.0.
Il s'agit d'un système de trois équations linéaires à trois inconnues. Il existe donc une méthode de résolution analytique.
On commence par le calcul du déterminant D = (z1y2-y1z2)xd+(x1z2-z1x2)yd+(y1x2-x1y2)zd
Si D est égal à 0.0, le rayon est parallèle à la facette et le calcul s'arête là.
Si D est différent de 0.0, u, t et v peuvent être calculés selon les formules suivantes :
u = ((ydz2-zdy2)x3+(x2zd-xdz2)y3+(xdy2-ydx2)z3)/D
v = ((y1zd-z1yd)x3+(xdz1-zdx1)y3+(ydx1-xdy1)z3)/D
t = ((y1z2-z1y2)x3+(x1z2+x2z1)y3+(x1y2-x2y1)z3)/D
Pour que le point d’intersection soit à l’intérieur du triangle ABC, il faut que :
- u soit positif ou nul,
- v soit positif ou nul,
- u+v soit inférieur ou égal à 1.0,
- t soit strictement positif.
Les optimisations classiques mises en œuvre autour de l'algorithme du lancer de rayons portent sur trois facteurs clés :
- optimisation des tests d'intersection,
- diminution du nombre de tests d'intersection,
- diminution du nombre de rayons primaires et diminution du nombre rayons secondaires.
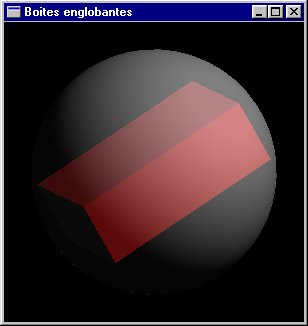
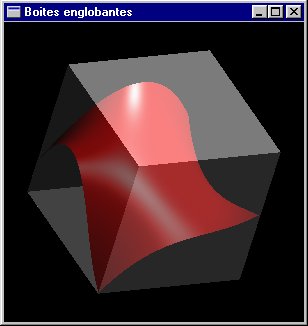
Optimisation des tests d'intersection : Les boites englobantes
Pour certaines catégories d'objet la réalisation de tests d'intersection entraîne une charge de calcul importante (par exemple, pour le tore il n'y a pas de solution analytique mais uniquement des solutions numériques par approximations successives). En englobant strictement chaque objet de la scène dans une "boite" géométrique simple (de test d'intersection rapide), on pourra réaliser une économie substantielle car un rayon provenant de l'extérieur de la boite englobante et qui ne la touche pas ne pourra pas toucher l'objet qu'elle contient. Ainsi en acceptant un petit calcul systématique il est possible d'obtenir des gains de temps globaux substantiels.
| Boites englobantes |
|
|
| Enter pour switcher entre affichages |
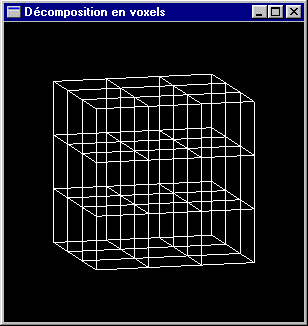
Décomposition en voxels de l'espace de la scène : Diminution du nombre de calculs d'intersections
Espace voxels : Un espace voxel est un espace décomposé en volumes élémentaires identiques généralement cubiques nommés voxels
(volume elements) (voir ci-dessous). Les voxels sont habituellement utilisés pour leur associer des informations qui seront considérées comme uniformes
sur l'intégralité du voxel.
Exemple : Une texture bitmap 3D peut être considérée comme un espace voxel où chaque voxel stocke une couleur.
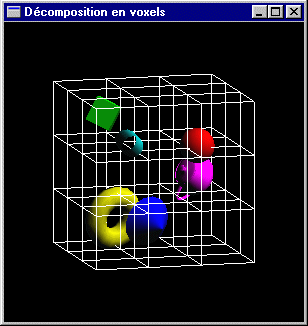
| Répartition des objets dans un espace voxels |
|
|
| Enter pour switcher entre affichages |
Dans le cadre du lancer de rayons, l'acquisition de connaissances sur la position des objets à l'intérieur de la scène peut éviter la réalisation obligatoire d'une recherche systématique d'intersections lors du test d'un rayon vis à vis de l'intégralité des objets de la scène. Décomposer l'espace en voxels et associer à chaque voxel la liste des objets qu'il inclut totalement ou partiellement (voir ci-dessus) permet cette acquisition. Ainsi, plutôt que de parcourir séquentiellement tous les objets de la scène à la recherche de l'intersection la plus proche de la source d'un rayon, on analyse les listes d'objets associées aux voxels, voxel après voxel sur le trajet du rayon depuis le voxel d'émission. Sitôt qu'une intersection est trouvée dans une liste d'objets (la plus proche des intersections lorsqu'il y en a plusieurs dans les objets d'une liste d'objets), il n'est plus nécessaire de parcourir d'autres voxels car toute autre intersection trouvée sera obligatoirement plus éloignée du point d'émission du rayon que celle que l'on vient de trouver.
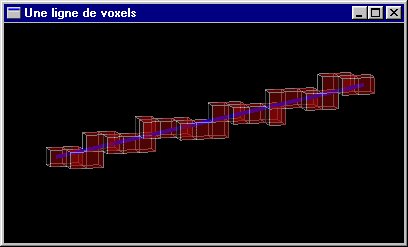
| Parcours d'un rayon dans un espace voxels |
|
|
|
Enter pour switcher entre affichages : rayon seul, rayon+voxels de Bresenham, rayon+tous les voxels traversé, trace du parcours du rayon dans les voxels (Espace pour avancer) |
Diminution du nombre de rayons tracés
Une solution simple pour diminuer le nombre de rayons primaires tracés consiste à effectuer préalablement au lancer de rayon un Z-Buffer des objets de la scène sur l'écran de visualisation. On saura ainsi quels sont les pixels en lesquels des objets apparaissent et donc quels sont les pixels pour lesquels il est nécessaire de lancer un rayon primaire et ceux pour lesquels c'est inutile.
Le problème de la diminution du nombre de rayons secondaires est complexe et ne sera pas traité ici.
9. Conclusion
Le lancer de rayons est correct du point de vue géométrique pour le placement des rayons lumineux à l'intérieur d'une scène.
Il est en revanche beaucoup moins correct du point de vue énergétique car les phénomènes que l’on désire rendre relèvent de transports d’énergie, aspect que le lancer de rayons ne traduit que partiellement. Ces phénomènes sont beaucoup plus complexes que ceux que l’on peut modéliser par de simples calculs géométriques.
Un avantage déterminant du lancer de rayons pour l'obtention d'images photo-réalistes est toutefois que cet algorithme permet de rendre les réflexions et les transparences.
Par rapport à un algorithme du Z-Buffer + Gouraud ou Phong, les images sont de bien meilleure qualité, mais les temps de calcul sont généralement considérablement plus longs (multipliés par 100, 1000 ou plus voire beaucoup plus).